Rep:Mod:ejr15

Enrique's transition states wiki page. It might take a while to load as there are lots of Jmols on here!

Introduction

Chemical systems are often explored by attempting to model a potential energy surface for the system based on the number of atoms and the structure of the molecules involved. This is often done using specialist software such as Gaussian. Once constructed this surface can then be investigated by attempting to find certain points such as minima or stationary points, which often correspond to possible products or transition structures that the system may generate. This can help us to learn more about the mechanisms the system may undergo and also give indications as to how it may react.

The transition state of a chemical system is defined as a stationary point on the potential energy surface of the system which has only one negative force constant (corresponding to one negative frequency) and has a gradient of zero. On a potential energy surface consisting of 3N-6 coordinates (where N = No of atoms in the system), the transition state has only one unique coordinate with a negative curvature which corresponds to this negative force constant. Similarly, a minimum on the potential energy surface corresponds to a point with a gradient of zero which has no negative force constants (corresponding to all its coordinates having a positive curvature) and hence only positive frequencies are seen.

Based on these principles, this experiment aimed to determine the transition states for a set of three different Diels alder reactions as well as analyse the properties of each reaction. This included visualising the MO's of the reactants, calculating the reaction free energy and reaction barrier energies, finding the intrinsic reaction coordinate (IRC) and recording the change in bond lengths as the reactions progressed. To achieve this, two different computational methods were used within Gaussian known as PM6 and B3LYP/6-31G(d). PM6 is a semiempirical method which relies on Hartree-Fock theory, but makes a number of approximations and uses experimental data in parts of its calculations. This makes the method very quick and inexpensive to run, but can cause inaccuracies to arise when its used as a result (especially in more complex molecules). In contrast, B3LYP/6-31G(d) is primarily a density functional theory (DFT) method which makes use of a basis set of atomic orbitals. The method relies on determining the one electron density of the system in order to attempt to solve the Schrodinger equation, but also uses Hartree-Fock theory to try and account for electron exchange using a combination of experimental and directly calculated parameters. It is hence described as a hybrid functional theory. This method is much more reliable as there are far fewer approximations compared to PM6, however it can be costly to run and often takes much longer to complete compared to other computational methods.https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:ejr15

Nf710 (talk) 00:38, 12 January 2018 (UTC) This is a good summary. Nice understanding of the 3N-6 dimensions of the PEs and the relative force conatants and a good understanding of the the quantum mechanical methods. You have clearly read beyond the script here. some equations and diagrams woudl have helps the discussion.

Exercise 1: Reaction of Butadiene with Ethylene

(Fv611 (talk) Good job across the whole exercise!)

Reaction summary

Figure 1: A reaction scheme for the Diels alder reaction between Butadiene and Ethylene. In this reaction, Butadiene acts as the diene and Ethylene acts as the Dienophile.

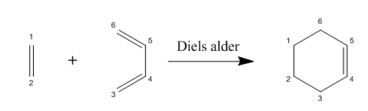
In this first exercise, a Diels Alder reaction (also known as a [4+2] cycloaddition) between Butadiene and Ethylene was investigated and is shown in figure 1.

In summary, the Butadiene and Ethylene reactants were optimised separately before being used to form a transition state at the PM6 level. This was verified to be the correct transition state by taking a frequency calculation, where only one negative frequency was seen which corresponded to the reaction path.Once completed, the resulting MO's of the reactants and the transition states were analysed and an MO diagram for the reaction was plotted.

The Cyclohexene product was then formed from the transition state by taking an Intrinsic Reaction Coordinate (IRC) and performing one final PM6 optimisation on the product structure obtained. This IRC was also used to monitor the change in C-C bond lengths as the reaction progressed.

Files used:

Reactants: File:EXERCISE1 DIELSALDER DIENEOPHILE EJR15.LOG , File:EXERCISE1 DIELSALDER DIENE NONPLANAR EJR15.LOG

Transition states: File:EXERCISE1 DIELSALDER TSPM6 EJR15.LOG

Products: File:EXERCISE1 DIELSALDER PRODUCTS PM6 EJR15.LOG

MO analysis

Figure 2: An MO diagram showing the formation of the Butadiene/Ethylene Transition state.

Figure 2 shows the MO diagram plotted for the reaction based on the frontier orbitals of the reactants and the transition state MO's that were produced from these during the optimisation (which are all shown below).

Ethene MO's

HOMO	LUMO

Butadiene MO's

HOMO	LUMO

Transition state MO's

HOMO-1	HOMO	LUMO	LUMO+1

Looking at the diagram and interactions shown above, it is clear that interactions between the frontier molecular orbitals only occur when they are of the same symmetry. This implies that a reaction can only take place if the orbitals involved in the reaction (ie: the HOMO and the LUMO) are of the same symmetry, allowing the reaction to occur. In contrast, frontier orbitals of opposing symmetry are unable to interact, hence the reaction is forbidden and cannot occur.

This makes sense as only orbitals of the same symmetry can produce an orbital overlap integral which is non-zero. When a symmetric-symmetric or antisymmetric-antisymmetric orbital interaction occurs, a net in-phase or net out of phase interaction occurs as both orbitals are of the same symmetry. This produces a Mo which is overall bonding or antibonding respectively.

In contrast, when a symmetric-antisymmetric orbital interaction occurs there is no net in-phase or out of phase interaction as the orbitals are of different symmetry. This produces an orbital overlap integral of zero as any parts of the orbitals that generate an in-phase interaction will be cancelled out by the parts that generate an out of phase interaction.

Change in C-C bond lengths

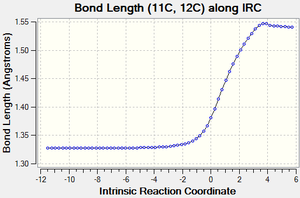
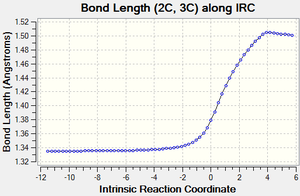
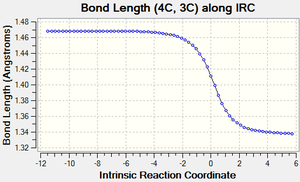
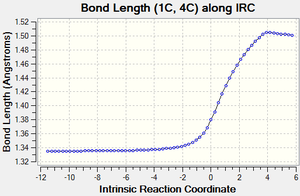
Figure 3: Graphs showing the change in C-C bond lengths of the reactants and Transition state as the reaction progressed. Generated from an IRC.

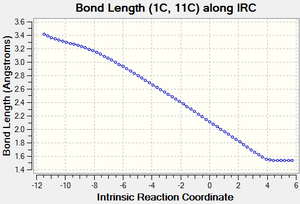
Figure 3 shows the changes in each C-C bond length over the course of the reaction. Looking at the reactants ethylene has a C=C double bond length of 1.34 Å, whilst butadiene has a C=C double bond length of 1.335 Å and a C-C single bond length of 1.47 Å.

In comparison the transition state has three C-C bond lengths of 1.38 Å (11C-12C, 2C-3C, 1C-4C), two new C-C bond lengths of 2.1 Å (1C-11C, 2C-12C) and one C-C bond length of 1.41 Å (4C-3C).

Finally, the product has one C=C bond length of 1.34 Å (4C-3C), three C-C bond lengths of 1.54 Å (11C-12C, 1C-11C, 2C-12C) and two C-C bond lengths of 1.50 Å (1C-4C, 2C-3C).

As the reaction proceeds, all the C=C double bonds in the reactants lengthen until they form C-C single bonds as seen in the product. In contrast, the existing C-C single bond in the Butadiene molecule shortens until it forms a C=C double bond and the distance between the ends of the reactants also shortens until two new C-C single bonds are formed.

Compared to the standard sp³ and sp² C-C bond lengths of 1.54 Å and 1.34 Å respectively, we can see that a number of the C-C bonds are slightly different to these. In the reactants, some of the sp³ and sp² C-C bonds are slightly shorter than the standard value due to the effects of conjugation. Similarly, in the product some of the C-C bonds are slighlty shorter than expected. This is due to the increased S character that some of these bonds posses (such as at bonds 2C-3C and 1C-4C).

As mentioned previously, the transition state also contains two new partially formed C-C bonds between the ends of the reactants and are 2.1 Å long. This is less than the Van de Waals radius of Carbon (1.70 Å), which implies that there is some sort of interaction occurring between these carbon atoms and makes sense considering that we are looking at two partially formed C-C bonds in the transition state. These bonds are also longer than the standard sp³ and sp² values since the bond hasn't fully formed yet.

Transition state vibration

Figure 4: The negative Transition state vibration that corresponds to the reaction path. It has a frequency of -950.09 cm^-1 (Click to animate)

Looking at figure 4, it is clear that the reaction occurs with synchronous formation of the two new c-c bonds between the ends of the diene and dienophile. This makes sense as the Diels alder reaction is known to occur via a concerted mechanism.

Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole

Reaction summary

Figure 5: Scheme showing the two possible diels alder reactions between cyclohexadiene and 1,3 - dioxole.

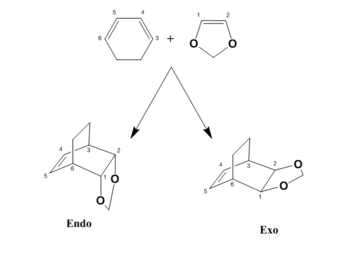
Similarly to the previous exercise, this task investigated the Diels alder reaction between cyclohexadiene and 1,3 - Dioxole. Unlike previously however, two possible products can be generated from this reaction depending on the orientation of the diene and are known as the Exo or Endo products (shown in figure 5). These products have slightly different transition states and final structures, which causes some of their energies and MO interactions to differ as a result.

The method used was as follows: each product was optimised using B3LYP/6-31G(d) before being used to find the resulting transition state. Each transition state was verified by taking a frequency calculation, which showed one negative frequency corresponding to the reaction path. From here, an IRC was then taken at the PM6 level and the reactants were retrieved from this and reoptimised to the B3LYP/6-31G(d) level.

The resulting MO's of the reactants, products and transition states were then analysed and the reaction energies/barriers for each product/TS were calculated using the energies generated by the B3LYP/6-31G(d) optimisations.

Files used:

Reactants:File:EXERCISE2 DIENOPHILE B3LYP REOPT SYMBREAK ejr15.LOG , File:EXERCISE2 DIENE REOPTIMISATIONFORMOS B3LYP ejr15.LOG

Transition states: File:EXERCISE2 TS EXO TSB3LYP ejr15.LOG , File:EXERCISE2 TS TSB3LYP 6-31GD ejr15.LOG

Products: File:EXERCISE2 PRODUCT ENDO OPT B3LYP ejr15.LOG , File:EXERCISE2 PRODUCT EXO B3LYP ejr15.LOG

MO Analysis

(Fv611 (talk) Good MOs and MO diagram. Could have extended a bit more on the differences in relative energies between endo and exo cases.)

Figure 6: An MO diagram showing the formation of the Cyclohexadiene/1,3 - dioxole transition state. Note that this diagram doesn't account for the slight differences in energies and orbital interactions between the exo and endo transition states.

Figure 6 shows the general MO diagram plotted for this reaction based on the interactions of the frontier molecular orbitals of the reactants. The transition state MOs generated by Gaussian can also be seen below.

Compared to the previous MO diagram from exercise 1 (Figure 2), this reaction appears to be an inverse electron demand Diels alder reaction as the frontier orbitals of the dienophile are raised above the diene. This occurs because the dienophile is much more electron rich compared to the diene, which causes its orbitals to be higher in energy as a result.

Nf710 (talk) 10:40, 12 January 2018 (UTC) You could have proven this quantitively by running both reactants on the same PES.

Transition state MO's

EXO HOMO-1	EXO HOMO	EXO LUMO	EXO LUMO+1

ENDO HOMO-1	ENDO HOMO	ENDO LUMO	ENDO LUMO+1

Reaction barriers/energies at the B3LYP/6-31G(d) level

	Reaction energy / Hartree	Reaction energy / kJmol-1	Reaction barrier / Hartree	Reaction barrier / kJmol-1
Exo Diels alder	-0.024303	-63.80	0.0683854	179.55
Endo Diels alder	-0.025672	-67.40	0.06087	159.81

The table above shows the calculated reaction energies and barriers for the Exo and Endo Diels alder reactions. Notably, these values suggest that the Endo reaction is both kinetically and thermodynamically favoured as it requires less energy to reach the endo transition state and it also appears the endo product is more exothermic than the exo product. This is unusual, as normally the exo product is more thermodynamically favourable product. This is likely to be due to two factors. Firstly, the endo product may be less sterically hindered in this case as it lacks the steric interactions between the CH₂ groups on the cyclohexadiene and the 1,3-dioxole as these groups face in opposite directions. Secondly, a secondary orbital interaction between the oxygens on the dienophile and the diene orbitals may also be present when forming the endo transition state,stabilising it and allowing it to form more quickly.

Secondary orbital interactions

ENDO HOMO	EXO HOMO

The HOMO transition state orbitals for the exo and endo reaction are shown above. Looking at the endo HOMO, there appears to be some sort of secondary orbital interaction occurring between the p-orbitals on the oxygen atoms of the Dienophile and the central lobes of the Diene. These interactions are in phase and so provide additional stabilisation to the endo transition state, which explains the endo reaction's reduced reaction barrier energy.

In comparison, the exo HOMO lacks these secondary interactions as the oxygen atoms of the Dienophile are facing away from the Diene and so cannot interact. This results in the exo transition state being higher in energy as it lacks these extra stabilising interactions that the endo transition state has.

Nf710 (talk) 10:42, 12 January 2018 (UTC) Were nice section your energies are correct and you have come to the correct conclusions. You could have given some diagrams to aid with the discussion. /

Exercise 3: Diels-Alder vs Cheletropic

Reaction summary

Figure 7: Reaction scheme showing all the Diels alder and Cheletropic reactions between Xylylene and SO₂ that were analysed.

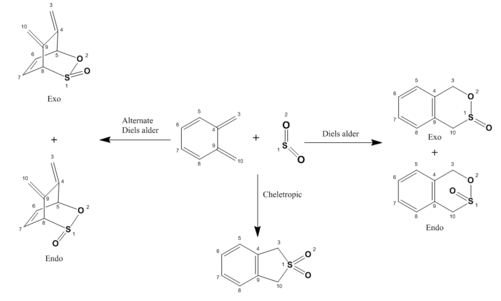
(Nice scheme Tam10 (talk) 15:14, 9 January 2018 (UTC))

In this final exercise, the reaction of Xylylene and SO₂ was investigated. This is a particularly unique case as the reactants can react either via a Diels alder reaction at one of the two diene sites or via a cheletropic reaction instead (all shown in figure 7). There is also the possibility of generating an exo or endo product for each diels alder reaction as mentioned in exercise 2, leading to five unique products being generated depending on which reaction occurs.

The method used was as follows: each product was constructed and optimised to the PM6 level before being used to find it's corresponding transition state. Each transition state was then verified by taking a frequency calculation, which showed one negative frequency that corresponded to the reaction path. From here, IRCs at the PM6 level were then taken for the main three reactions that occur (the endo/exo Diels alder and Cheletropic reactions at carbons C3 and C10) and the reactants were retrieved from this and reoptimised to the PM6 level separately.

The resulting reaction energies and barriers were then calculated from these optimised molecules using the energies generated from the PM6 optimisations.

Files used:

Reactants: File:EXERCISE3 DIENOPHILE PM6 EJR15.LOG, File:EXERCISE3 DIENE PM6 EJR15.LOG

Transition states: File:EXERCISE3 CHELEOTROPIC PM6 TS BERRY EJR15.LOG,File:EXERCISE3 EXO TS PM6RETRY ejr15.LOG , File:Exercise3 EJR15 endo TSPM6.LOG

Products: File:EXERCISE3 CHELEOTROPIC PM6 PRODUCT. EJR15LOG,File:EXERCISE3 PRODUCT EXO PM6.LOG ,File:EXERCISE3 EJR15 endo product.LOG

Alternate Transition states: File:EXERCISE3 TS EXO TS PM6 alternate berry EJR15.LOG, File:EXERCISE3 TS ENDO BERRYPM6 alternate EJR15.LOG

Alternate products: File:EXERCISE3 EXO PRODUCT PM6 ALTERNATE EJR15.LOG, File:EXERCISE3 ENDO PRODUCT PM6 alternate.LOG

("Berny" indicates the algorithm used, and holds little to no significance in the geometry itself Tam10 (talk) 15:14, 9 January 2018 (UTC))

Comparison of IRCs

The table below shows the IRCs of the main 3 reactions (The endo/exo Diels alder and Cheletropic reactions across C3 and C10) that can occur along with animations showing the formation of each of the products.

Endo IRC	Exo IRC	Cheletropic IRC

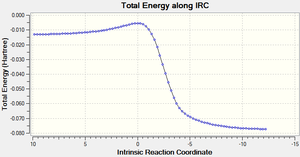
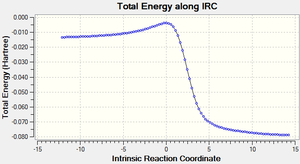
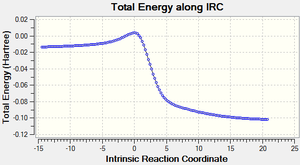
(Click to animate)

Looking at each of the animations, it is clear that some notable structural changes occur as the reaction progresses. In particular, the 6 membered ring in the Xylylene molecule appears to become delocalised and each of the C-C bonds in the ring appear to shorten until they are all the same length. This occurs because during the reaction a benzene ring is formed from the second diene and the new double bond adjacent to the SO₂ molecule. This new Benzene fragment is highly aromatic and delocalised compared to the cyclohexadiene fragment that preceded it, causing each C-C bond length inside the ring to all decrease to a length between that of a single and double C-C bond. The formation of this benzene ring also helps drive the reaction to form the product due to the significantly increased stability these products have compared to the original xylylene reactant.

Reaction barriers/energies at the PM6 level

	Reaction energy / Hartree	Reaction energy / kJmol-1	Reaction barrier / Hartree	Reaction barrier / kJmol-1
Exo Diels alder	-0.037397	-98.19	0.033228	87.24
Endo Diels alder	-0.037155	-97.55	0.031707	83.25
Cheletropic	-0.058852	-154.52	0.040209	105.57

The table above shows the calculated Reaction barriers/energies for the three previously shown reactions. These numbers indicate that as expected, the endo Diels alder reaction has the lowest energy transition state and so is the kinetic product. This is as expected as in the endo conformation, the second oxygen atom on the SO₂ molecule can undergo a secondary orbital interaction with the diene which helps to stabilise the transition state. The exo reaction in comparison has a slightly higher energy transition state as the oxygen atom cannot interact with the diene in this conformation. The exo product is slighlty more thermodynamically favoured than the endo product however due to the reduced steric hinderance the oxygen experiences when it is in the equatorial position of the ring (see figure 7). Interestingly, it turns out that the cheletropic reaction is the most thermodynamically favoured outcome, yet it has the largest reaction barrier and so is much more difficult to form as a result.

All of these results have been illustrated in the reaction profile shown in figure 8.

Figure 8: A reaction profile showing the main 3 reactions that can occur between Xylylene and SO₂.

(Use straight lines for reaction profiles like this Tam10 (talk) 15:14, 9 January 2018 (UTC))

An alternative Diels alder reaction

As mentioned previously, there is an alternative diels alder reaction that can occur on the cyclohexadiene fragment of the xylylene molecule, generating either an exo or endo product. The table below shows the calculated reaction barriers and energies for these reactions at this second diene site:

	Reaction energy / Hartree	Reaction energy / kJmol-1	Reaction barrier / Hartree	Reaction barrier / kJmol-1
Exo Diels alder	0.008453	22.19	0.046202	121.30
Endo Diels alder	0.006758	17.74	0.043218	113.47

Compared to the previous three reactions at the primary diene site, it is clear that both the endo and exo reactions are much more kinetically and thermodynamically unfavourable in comparison. Both reactions are endothermic compared to the reactants and they also require much more energy compared to the previous reactions in order to reach their transition states, which explains why these two reactions are rarely seen as a result. The main reason for this is that no benzene ring is formed during the reaction, which causes the generated products to be much less stable compared to the previous ones as a result.

Conclusion

Overall, these three tasks have shown that it is possible to accurately locate and model the products, reactants and transition states of various Diels alder reactions (in addition to a cheletropic reaction) using both semiempirical and DFT methods. It is also clear that further analysis of these structures such as visualising their MO's, modelling their expected frequencies and calculating their free energies is also very feasible using these methods, as accurate results which fit well with the theory and experimental observations were seen. This opens up the possibility of modelling these types of reactions before conducting a physical experiment in order to try and predict it's outcome, which should save money and time.

In future, these experiments could be expanded by attempting to model larger systems as the molecules modelled in these exercises were quite small and so are reasonably predictable. This may require the use of more complex computational methods however in order to accurately model these systems, and so would require some investigation beforehand in order to determine which methods match the theory and experimental observations the best. Other types of pericyclic reactions (such as [3+2] cycloadditions or sigmatropic rearrangements) could also be investigated to further test if these computational methods could be applied to other similar reactions.