Module 3- Transition states and Reactivity

Introduction

The Cope Rearrangement

The Cope Rearrangement is an example of a [3,3]-sigmatropic shift rearrangement and is generally accepted to proceed in a concerted manner via either the "chair" or "boat" transition states. This project examines the Cope rearrangement of 1,5-hexadiene to determine the preferred energy minima. This is done by locating the low-energy minima and transition structures on the 1,5-hexadiene potential energy surface. Computational methods are used to calculate the energies of the structures and transition states.

Fig 1- the Cope Rearrangement

Optimising the Reactants and Products

1,5-hexadiene has many conformers with the central four atoms arranged in either the anti or the gauche conformation. Several of these structures were optimised in GaussView using the HF/3-21G level of theory and were then symmetrized to find the point group.

It is expected that the gauche conformers would be higher in energy. This is because the anti conformers have the lowest steric hindrance as the carbons are kept as far from each other as possible. However, the conformer with the lowest energy is in fact a gauche conformer (gauche 3). This is thought to be due to favourable Van der Waals Hydrogen interactions as well as C-H σ* - C=C π orbital overlap.^[1].

The C_i anti conformer was optimised again but using a higher level of theory; B3LYP/6-31G* DFT. Parameters of the two structures were compared.

Table 2- Comparison of geometries for C_i anti conformer
Property	HF/3-21G	B3LYP/6-31G*
Point group	C_i	C_i
Energy (a.u.)	-231.6925353	-234.611711
C=C bond length (Å)	1.32	1.33
sp²C(2)-sp³C(3) bond length (Å)	1.50	1.51
C(3)-C(4) bond length (Å)	1.55	1.55
C(1)-C(2)-C(3) angle (^o)	124.8	125.3
C(2)-C(3)-C(4) angle (^o)	111.4	112.7
C(1)-C(2)-C(3)-C(4) dihedral angle (^o)	114.7	118.3

The energy was calculated as being more negative for the optimisation using a higher level of theory (B3LYP/6-31G*) indicating that this is the more accurate method. However, the energies cannot be compared because they were calculated using different levels of theory. The largest difference between the two structures was in the dihedral angles of C(1)-C(4) but overall the optimisation methods gave very similar results. The bond lengths compared well to the expected bond lengths (C-C 1.54Å, C=C 1.34Å^[2]).

Frequency Calculation

Frequency analysis can be used to determine whether a structure has been correctly optimised. If all the vibrations are positive then the structure is indeed at an energy minima, if there is one negative vibration the structure is in a transition state. A frequency analysis was carried out on the C_i anti conformer that had been optimised using the DFT, B3LYP/6-31G* method and basis set. Table 3 shows some of the key vibrations from the optimisation.

Table 3- Some selected vibrations for C_i anti conformer
Frequency (cm^-1)	Intensity	Description
1735	18.2	C=C stretch
3031	53.5	alkane C-H stretch
3079	36.1	alkane C-H stretch
3137	56.1	alkene C-H stretch
3156	14.6	alkene C-H stretch
3243	45.5	alkene C-H stretch

Fig 2- the IR spectrum of C_i anti 1,5-hexadiene

These frequencies were calculated using a harmonic potential approximation instead of an anharmonic potential and so have a 10% error associated with them. A higher level basis set would be needed to improve the accuracy.

The output file from the frequency calculation contains information about the thermodynamic and kinetic parts that make up the energy of the molecule. This allows the enthalpy and free energy of dissociation to be calculated.

Table 4- vibrational temperatures from log file
Type of energy	Value (a.u.)
Zero-point correction	0.142493
Thermal correction to energy	0.149845
Thermal correction to enthalpy	0.150790
Thermal correction to Gibbs free energy	0.110895
Sum of electronic and zero-point energies	-234.4691219
Sum of electronic and thermal energies	-234.462867
Sum of electronic and thermal enthalpies	-234.460922
Sum of electronic and thermal freeeEnergies	-234.500817

The meaning of the terms in table 4 are as follows:

Sum of electronic and zero-ponit energies - the potential at 0 K including the zero-point vibrational energy (E=E_elec + ZPE)
Sum of electronic and thermal energies - the energy at 298.15 K and 1 atm of pressure (standard conditions) which includes the translational, rotational and vibrational energy modes (E= E +E_vib +E_rot +E_trans).
Sum of electronic and thermal enthalpies - contains the correction for RT (H=E +RT)
Sum of electronic and thermal free energies - includes the entropic contribition to free energy (E=H -TS)

Optimising the 'Chair' and 'Boat' transition structures

It is possible to use computational methods to optimise not just the reactants and products but the transition states as well. In the Cope rearrangement the reaction can go through either a "chair" (C_2h) or a "boat" (C_2v) transition state. An allyl fragment (CH₂CHCH₂) was drawn out and optimised using the HF/3-21G level of theory. Next, two optimised allyl fragments were placed together to form the chair transition state making sure that the terminal carbons were around 2.2Å apart. This transition state was then optimised using two different methods. The first is the TS(berny) method whereby the force contant matrix (the Hessian) is calculated and then recalculated through optimisation. The initial guess has to be accurate or the resulting structure will be at a false minima. The second method in the frozen coordinate method in which the reaction coordinate is "frozen" whilst the rest of the molecule is optimised. The molecule is then unfrozen and the transition state is optimised again. In this method it is not necessary to calculate the whole Hessian. Both methods used the HF/3-21G level of theory.

The TS(berny) method

An "Opt + Freq" calculation was run with the "optimization to a TS (Berny)" option selected. The force constants were calculated "once" and "Opt=NoEigen" was added into the addition keywords section. The energy of this transition state was calculated to be -231.619322 a.u. and looking at the frequencies showed that there was one negative frequency at 818 cm^-1. This vibration corresponded to the Cope Rearrangement. The distance between the terminal carbons was 2.0204Å.

Fig ?- imaginery vibration

The frozen coordinate method

The distance between the terminal carbons on the allyl fragments was set at 2.2Å and an optimization run to a minimum. Once the molecule had optimised it was then re-optimised except that the "derivative" option was chosen for the terminal allyl carbons and the calculation was run optimised to a TS (Berny) state using the same parameters as before. The energy of the TS was calculated to be -231.6193222 a.u. and there was also a negative frequency at 818 cm^-1 corresponding to the Cope Rearrangement. The distance between the terminal carbons was 2.0207Å. compare the two TS

Optimising the "boat" transition state

The TS(QST2) method was used to calculate the transition state for the boat structure. The C_i anti 1,5-hexadiene was used as the reactant and the product molecule but all the atoms were renumbered so that the atoms in the product were in the correct place. This job was submitted but did not finish correctly. This was because these conformations were too far from the correct structure of the transition state to converge.

Fig 3 - the altered geometries of the reactant and product
Reactant	Product

To combat this, the geometries of the reactant and product were altered so as to be closer to the transition state. The C(2)-C(3)-C(4)-C(5) dihedral angle was set to 0_o and the C(2)-C(3)-C(4) (and the corresponding C(3)-C(4)-C(5)) was set to 100_o. The job was then resubmitted and this time the transition state was correctly generated. This transition state had an energy of -231.602802 a.u. and one imaginary vibration at -840 cm_-1 indicating that the molecule was at a transition state.

Fig 4 - the QST2 Transition State

IRC

It is very difficult to predict which conformer will result from a transition state but there is a method in Gaussian called IRC (Intrinsic Reaction Coordinate)that follows the minimum pathway along the potential energy surface to the local minima. At each step a small geometric change is made along the direction of the steepest potential gradient. This method can allow the conformation associated with the transition state to be determined. An IRC calculation was submitted using the chair transition state optimised using the frozen coordinate method with the number of steps set to 50. After 25 steps the calculation converged to give a structure with energy = -213.672038 a.u. However, it also had an imaginary frequency at -817 cm^-1 indicating that this was still a transition state.

Fig 6 - the steps in the IRC method

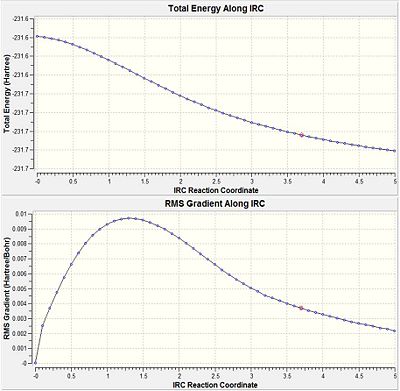To try and find the correct minimum the calculation as rerun as before except that the force constant was computed at each step. This time the calculation converged after 47 steps to give an energy of -231.691649 a.u. All the frequencies were positive indicating a true minimum had been found. This structure corresponded to the gauche C₂ conformer.

Fig 8 - the steps in the IRC method

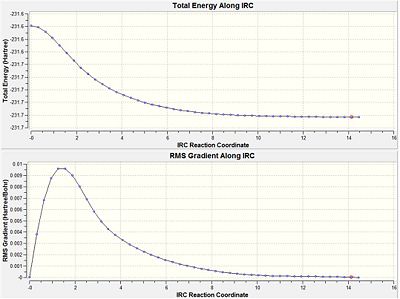Calculating the activation energies

In order to accurately calculate the activation energies of the reaction the transition states were optimised using a higher level of theory; B3LYP/6-31G(d). The log file from each optimisation gave information as to energies at 0K and 295K. When compared to the energies for the starting reactant (anti C₂ 1,5 hexadiene) the activation energy could be calculated.

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.6193	-231.4667	-231.4613	-234.5569	-234.4149	-234.4090
Boat TS	-231.6028	-231.4509	-231.4453	-234.5431	-234.4023	-234.3951
*Reactant (anti2)*	-231.693	-231.540	-231.533	-234.612	-234.469	-234.462

The activation energies were calculated in kcal/mol and are shown in the table below. The energies for each method show a marked difference but cannot be compared.

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.81	45.18	33.89	33.26	33.5 ± 0.5
ΔE (Boat)	55.85	55.22	42.04	41.42	44.7 ± 2.0

compare, which is better method? which TS is lower-prefered

The Diels-Alder Cycloaddition

The Diels-Alder reaction is an example of a [4π+2π] pericyclic cycloaddition between a diene and a dienophile. The HOMO/LUMO on the diene interacts with the HOMO/LUMO on the dienophile. One such Diels-Alder reaction occurs between cis-butadiene and ethylene. First the structures of cis-butadiene and ethylene were optimised using the AM1 semi-empirical molecular orbital method. The HOMO and LUMO MO's of cis-butadiene and ethylene are shown below.

Table ?- The HOMO and LUMO MO's for cis-butadiene and ethylene
Reactant	MO	Symmetry
cis-butadiene HOMO		asymmetric
cis-butadiene LUMO		symmetric
ethylene HOMO		symmetric
ethylene LUMO		asymmetric

The transition state in this reaction was optimised using the frozen coordinate method as described above using the Am1 semi-empirical molecualr orbital method. Then it was re-optimised using the higher theory (B3LYP/6-31G(d)).

Fig ? - the steps in the IRC method

Table ?- The calculated energies for the transition state
Method	Energy/ a.u.	Imaginary frequency cm^-1	C-C bond length/ Å
AM1 semi-empirical	0.1162913	-955	2.12
DFT/B3LYP/6-31G(d)	-234.54896	-524	2.27

lower: C=C bond length = 1.38, C-C bond length =1/39 higher:C=C bond length = 1.38, C-C bond length=1.40 literature values

The molecular orbitals for the HOMO and LUMO were ...

Fig ? - HOMO and LUMO molecular orbitals of the transition state
Molecular Orbital		Energy (a.u.)	Symmetry
LUMO		0.023	Symmetric
HOMO		-0.323	Anti-symmetric

maleic anhydride diels-alder:

lower,endo: energy= 0.00749388 imaginery frequency= -826 higher, endo: energy=

lower, exo:energy= higher, exo:energy=

↑ B.G. Rocque, J.M. Gonzales, H.F. Schaefer III, Mol. Phys., 2002, 100, 441[1]
↑ http://www.wiredchemist.com/chemistry/data/bond_energies_lengths.html

[1] B.G. Rocque, J.M. Gonzales, H.F. Schaefer III, Mol. Phys., 2002, 100, 441[1]

[2] ttp://www.wiredchemist.com/chemistry/data/bond_energies_lengths.html

[1]

[2]