Rep:Mod:eb108m6

Module 3- Transition states and Reactivity

Introduction

Using only computational methods this project attempts to predict the behaviour and outcome of the Cope Rearrangement and the Diels-Alder reaction. Various levels of theory are used; the Hartree-Fock/3-21G method, the AM1 semi-empirical molecular orbital method and the DFT/B3LYp/6-31G* method and basis set.

The Cope Rearrangement

Fig 1- the Cope Rearrangement

The Cope Rearrangement is an example of a [3,3]-sigmatropic shift rearrangement and is generally accepted to proceed in a concerted manner via either the "chair" or "boat" transition states. This project examines the Cope rearrangement of 1,5-hexadiene to determine the preferred energy minima. This is done by locating the low-energy minima and transition structures on the 1,5-hexadiene potential energy surface. Computational methods are used to calculate the energies of the structures and transition states.

Optimising the Reactants and Products

1,5-hexadiene has many conformers with the central four atoms arranged in either the anti or the gauche conformation. The molecule was drawn out in Gaussview and the carbons were arranged in an anti-periplanar relationship. This was then optimised using the HF/3-21G level of theory and then symmetrized to find the point group. This gave 1,5 hexadiene in the anti conformation with C_i symmetry. Several other anti and gauche conformations were also optimised after manipulating the molecule.

Table 1 - Several conformers of 1,5-hexadiene

Conformation
Energy/ a.u.	-231.6925	-231.6910	-231.6891	-231.6892	-23`.6917	-231.6927
Point Group	Ci	C1	C2h	C1	C2	C1

It is expected that the gauche conformers would be higher in energy than the anti conformers and this is the case for the majority This is because the anti conformers have the lowest steric hindrance as the carbons are kept as far from each other as possible. In the majority of cases this is true. However, the conformer with the lowest energy is in fact a gauche conformer (gauche 3 in the table; -1.4539 x 10⁵ kcal/mol). This is thought to be due to favourable Van der Waals Hydrogen interactions and well as C-H σ* - C-C π orbital overlap leading to stabilisation of the molecule.. The energies are however, extremely similar and would inter-convert at room temperature.

The C_i anti conformer was optimised again but using a higher level of theory; DFT/B3LYP/6-31G* DFT. Parameters of the two structures were compared. The DFT/B3LYP allows us to determine the electronic structure of a many-electron system. The 6-31G* is a much more accurate basis set than 3-21G.

Table 2- Comparison of geometries for C_i anti conformer

Property	HF/3-21G	B3LYP/6-31G*
Point group	Ci	Ci
Energy (a.u.)	-231.69254	-234.6117
C=C bond length (Å)	1.32	1.33
sp2C(2)-sp3C(3) bond length (Å)	1.50	1.51
C(3)-C(4) bond length (Å)	1.55	1.55
C(1)-C(2)-C(3) angle (o)	124.8	125.3
C(2)-C(3)-C(4) angle (o)	111.4	112.7
C(1)-C(2)-C(3)-C(4) dihedral angle (o)	114.7	118.3

The energy was calculated as being more negative for the optimisation using a higher level of theory (B3LYP/6-31G*) indicating that this is the more accurate method. However, the energies cannot be compared because they were calculated using different levels of theory. The largest difference between the two structures was in the dihedral angles of C(1)-C(4) but overall the optimisation methods gave very similar results. The bond lengths compared well to the expected bond lengths (C-C 1.54Å, C=C 1.34Å).

Frequency Calculation

Frequency analysis can be used to determine whether a structure has been correctly optimised. If all the vibrations are positive then the structure is indeed at an energy minima, if there is one negative vibration the structure is in a transition state. Essentially the frequencies of the molecule come from the curvature of the potential energy surface and are computed by calculating the second derivative of this potential energy. A frequency analysis was carried out on the C_i anti conformer that had been optimised using the DFT, B3LYP/6-31G* method and basis set. Table 3 shows some of the key vibrations from the optimisation. log file

Table 3- Key frequencies from the C_i anti conformer

wavenumber cm-1	vibration	intensity	type of vibration
1734		18.1	C=C stretch
3031		53.6	alkane C-H stretch
3079		35.9	alkane C-H stretch
3137		56.0	C-H stretch
3156		14.7	alkene C-H stretch
3234		45.5	alkene C-H stretch

Fig 2- the IR spectrum of C_i anti 1,5-hexadiene

These frequencies were calculated using a harmonic potential approximation instead of an anharmonic potential and so have a 10% error associated with them. A higher level basis set would be needed to improve the accuracy.

The output file from the frequency calculation contains information about the thermodynamic and kinetic parts making up the energy of the molecule. This allows the enthalpy and free energy of dissociation to be calculated.

Table 4- vibrational temperatures from log file

Type of energy	Value (a.u.)
Zero-point correction	0.142493
Thermal correction to energy	0.149845
Thermal correction to enthalpy	0.150790
Thermal correction to Gibbs free energy	0.110895
Sum of electronic and zero-point energies	-234.46912
Sum of electronic and thermal energies	-234.46287
Sum of electronic and thermal enthalpies	-234.4609
Sum of electronic and thermal freeeEnergies	-234.5008

The meaning of the terms in table 4 are as follows:

• Sum of electronic and zero-ponit energies - the potential at 0 K including the zero-point vibrational energy (E=E_elec + ZPE)
• Sum of electronic and thermal energies - the energy at 298.15 K and 1 atm of pressure (standard conditions) which includes the translational, rotational and vibrational energy modes (E= E +E_vib +E_rot +E_trans).
• Sum of electronic and thermal enthalpies - contains the correction for RT (H=E +RT)
• Sum of electronic and thermal free energies - includes the entropic contribition to free energy (E=H -TS)

Optimising the 'Chair' and 'Boat' transition structures

It is possible to use computational methods to optimise not just the reactants and products but the transition states as well. During the Cope rearrangement the reaction can go through either a "chair" (C_2h) or a "boat" (C_2v) transition state.

Optimising the Chair conformation

An allyl fragment (CH₂CHCH₂) was drawn out and optimised using the HF/3-21G level of theory. Next, two optimised allyl fragments were placed together to form the chair transition state making sure that the terminal carbons were around 2.2Å apart. This transition state was then optimised using two different methods. The first is the TS(berny) method whereby the force contant matrix (the Hessian) is calculated and then recalculated through optimisation. The initial guess has to be accurate or the resulting structure will be at a false minima. The second method in the frozen coordinate method in which the reaction coordinate is "frozen" whilst the rest of the molecule is optimised. The molecule is then unfrozen and the transition state is optimised again. In this method it is not necessary to calculate the whole Hessian. Both methods used the HF/3-21G level of theory.

The TS(berny) method

An "Opt + Freq" calculation was run with the "optimization to a TS (Berny)" option selected. The force constants were calculated "once" and "Opt=NoEigen" was added into the addition keywords section. This keyword stops the calculation from crashing if more than one imaginary frequecy is detected throughout the optimisation process. The energy of this transition state was calculated to be -231.61932 a.u. (-1.4534 x 10⁵ kcal/mol) and looking at the frequencies showed that there was one negative frequency at -818 cm^-1. This imaginary frequency corresponds to the bond breaking/forming process in the Cope rearrangement and from this we can tell that this process occurs in a concerted manner. This vibration corresponded to the Cope Rearrangement. The distance between the terminal carbons was 2.0204Å. log file

Fig 3- the imaginary vibration

The frozen coordinate method

The distance between the terminal carbons on the allyl fragments was frozen at 2.2Å along the reaction coordinate and an optimization run to a minimum. Once the molecule had optimised these distances were then "unfrozen" and the molecule was re-optimised. This time the "derivative" option was chosen for the terminal allyl carbons and the calculation was optimised to a TS (Berny) state using the same method as previously. The energy of the TS was calculated to be -231.61932 a.u. (-1.4534 x 10⁵ kcal/mol) and there was also a negative frequency at 818 cm^-1 corresponding to the Cope Rearrangement. The distance between the terminal carbons was 2.02Å. Both alternative methods for optimising the transition state gave remarkably similar results. The C-C bond lengths and the wavenumbers of the imaginary frequencies were the same. The energy was marginally lower when the frozen coordinate method was used but was negligable. log file- step 1, log file- step 2

Fig 4- the imaginary vibration

Optimising the "boat" transition state

The TS(QST2) method was used to calculate the transition state for the boat structure. In this method the reactant and product are specified and the calculation finds the transition state between them. The configurations of the reactant and product have to be close to the transition state structure or the calculation will fail. The C_i anti 1,5-hexadiene was used as the reactant and the product molecule. All the atoms were renumbered so that the atoms in the product were in the correct place. This job was submitted but did not finish correctly. This was because these conformations were too far from the correct structure of the transition state to converge.

Table 5- the numbered product and reactant

Reactant	Product

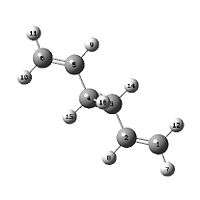To combat this, the geometries of the reactant and product were altered so as to be closer to the transition state. The C(2)-C(3)-C(4)-C(5) dihedral angle was set to 0_o and the C(2)-C(3)-C(4) (and the corresponding C(3)-C(4)-C(5)) was set to 100_o. The job was then resubmitted and this time the transition state was correctly generated. This transition state had an energy of -231.6028 a.u. (-1.433 x 10⁵ kcal/mol) and one imaginary vibration at -840 cm^-1 indicating that the molecule was at a transition state. log file

Table 6- the numbered product and reactant - altered geometry

Reactant	Product

Fig 5- the imaginary vibration of the boat transition state

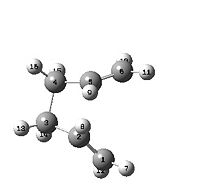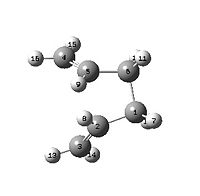The energy for the boat transition state was calculated to be slightly higher and therefore slightly more unstable. The wavenumber for the imaginary frequency was lower than for the chair transition state. However the motion of the frequency still showed the bond breaking/forming process happening in a concerted manner.

The Intrinsic Reaction Coordinate method

It is very difficult to predict which conformer will result from a transition state but there is a method in Gaussian called IRC (Intrinsic Reaction Coordinate)that follows the minimum pathway along the potential energy surface to the local minima. At each step a small geometric change is made along the direction of the steepest potential gradient. This method can allow the conformation associated with the transition state to be determined. An IRC calculation was submitted using the chair transition state optimised using the frozen coordinate method with the number of steps set to 50. After 25 steps the calculation converged to give a structure with energy = -231.6720 a.u. (-1.4538 x 10⁵ kcal/mol).However, it also had an imaginary frequency at -817 cm^-1 indicating that this was still a transition state. (log file too large to upload)

Fig 6 - the structure calculated using the IRC method

Fig 7 - the steps in the IRC method

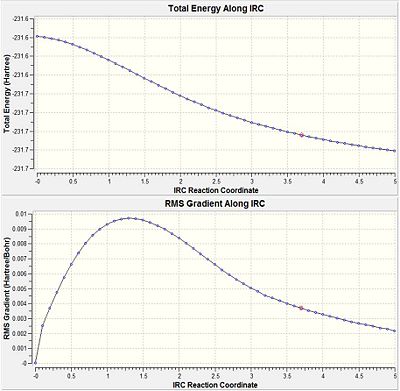To try and find the correct minimum the calculation as rerun as before except that the force constant was computed at each step. This is a much more expensive method but it is a lot more reliable. This time the calculation converged after 47 steps to give an energy of -231.6916 a.u. (-1.4539 x 10⁵ kcal/mol). This structure corresponded to the gauche C₂ conformer. (log file too large to upload)

Fig 8 - the structure calculated using the IRC method

Fig 9 - the steps in the IRC method

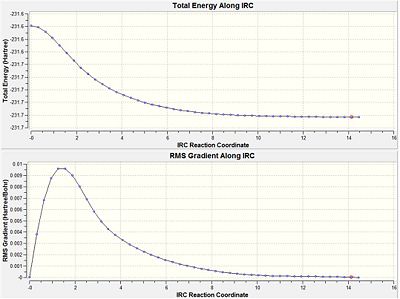Calculating the activation energies

In order to accurately calculate the activation energies of the reaction the transition states were optimised using a higher level of theory; B3LYP/6-31G(d). The log file from each optimisation gave information as to energies at 0K and 295K. When compared to the energies for the starting reactant (anti C₂ 1,5 hexadiene) the activation energy could be calculated. log file - chair, log file - boat, log file- reactant

Table 6 - the calculated energies for the transition states

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.6193	-231.4667	-231.4613	-234.5569	-234.4149	-234.4090
Boat TS	-231.6028	-231.4509	-231.4453	-234.5431	-234.4023	-234.3951
Reactant (anti2)	-231.693	-231.540	-231.533	-234.612	-234.469	-234.462

The energies calculated using the B3LYP/6-31G* level of theory were significantly more negative indicating that this method and basis set is more accurate and calculates the transition states to be more stable. The activation energies were calculated in kcal/mol and are shown in the table below. The energies for each method show a marked difference.

Table 7 - the activation energies for the transition states

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.81	45.18	33.89	33.26	33.5 ± 0.5
ΔE (Boat)	55.85	55.22	42.04	41.42	44.7 ± 2.0

The results calculated using the HF/3-21G level of theory do not correspond well to the literature values at 0K. However the B3LYP/6-31G* method and basis set yielded activation energies in close agreement with the literature. We can also see that the activation energy for the chair transition state is lower than for the boat transition state and were the Cope Rearrangement to be determined by kinetics then it would proceed via the chair transition structure.

The Diels-Alder Cycloaddition

The Diels-Alder reaction a [4π+2π] pericyclic cycloaddition between a diene and a dienophile to form a substituted cyclohexene system. The HOMO/LUMO on the diene interacts with the HOMO/LUMO on the dienophile and the reaction can occur in a concerted stereospecific fashion or not depending on the number of pi electrons.

Diels-Alder reaction between cis-butadiene and ethylene

One such Diels-Alder reaction occurs between cis-butadiene and ethylene.

Fig 10 - the steps in the IRC method

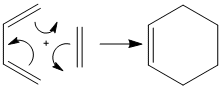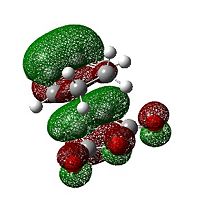
The Frontier Orbitals of Cis-butadiene and ethylene

The structures of cis-butadiene and ethylene were optimised using the AM1 semi-empirical molecular orbital method and the HOMO and LUMO MO's of both molecules were visualised. The symmetry of the orbitals was defined as being symmetric or anti-symmetric with respect to the plane of reflection. Only orbitals with the same symmetry properties can interact. Therefore it is possible to see that the HOMO on cis-butadiene can interact with the LUMO on ethylene. This corresponds to electron density from the HOMO of cis-butadiene going into the unoccupied π LUMO of ethylene weakening the double bond and leading to the breaking of this double bond. Also, the HOMO on ethylene can interact with the LUMO of cis-butadiene. This corresponds to the formation of the two C-C σ bonds. log file - ethylene, log file - cis-butadiene

Table 8- The HOMO and LUMO MO's for cis-butadiene and ethylene

Reactant	LCAO	MO	Symmetry
cis-butadiene HOMO			asymmetric
cis-butadiene LUMO		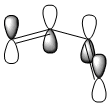	symmetric
ethylene HOMO		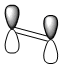	symmetric
ethylene LUMO		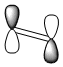	asymmetric

Optimising the Transition State

The transition state in this reaction was optimised using the frozen coordinate method as described above. The AM1 semi-empirical molecular orbital method was used with the bond forming carbons frozen 2.2Å from each other and the molecule was optimised to a minimum. It was then optimised to a TS(berny) with the distances unfrozen. Finally, it was run as an opt+freq using the higher theory (B3LYP/6-31G(d)). log file- Am1 semi-empirical method, log file - DFT/B3LYP method

Table 9- The calculated energies for the transition state

Method	Energy/ a.u.	Imaginary frequency/ cm-1	terminal C-C bond length/ Å
AM1 semi-empirical	0.1162913	-955	2.12
DFT/B3LYP/6-31G(d)	-234.5490	-524	2.27

There is a very large difference in calculated energy between the two levels of theory with the B3LYP/6-31G* method and basis set giving a much more stable structure. Clearly, the higher level of theory is much more accurate. The calculated wavenumbers for the imaginary frequencies were also very different. This to be expected as the frequencies are calculated from the second derivative of the potential energy slope and with such a marked difference in energies it is unsurprising that the slope of the potential energy surface is very different in both methods. The motion of the imaginary frequency shows that the formation of the two bonds occurs in a synchronous manner. The lowest positive frequency is 136 cm^-1 and shows no evidence of the concerted reaction mechanism.

Fig 11- the imaginary vibration of the boat transition state

The AM1 semi-empirical method calculated the C=C bond lengths as 1.38 Å and the C-C bond lengths as 1.39 Å. The B3LYP method calculated the cis-butadiene C-C bond length to be 1.40Å which lies between the literature values for a C-C bond (1.54 Å) and for a C=C bond ( 1.34). This suggests that this single bond is in the process of forming a double bond. The cis-butadiene C=C bonds were calculated to be 1.38 Å which is longer than the literature value suggesting that these double bonds are partway to becoming single bonds. Finally, as the above table shows the distance between the terminal carbons on cis-butadiene and ethylene (i.e. the partially formed single bonds) was calculated to be 2.27Å. This is smaller than the Van der Waals radius of two carbon atoms (3.40Å . showing that the cis-butadiene and ethylene are much closer together than they would be unless a bond is forming between them.

The molecular orbitals for the HOMO and LUMO were visualised.

Table 11 - HOMO and LUMO molecular orbitals of the transition state

Molecular Orbital		Energy (a.u.)	Symmetry
LUMO		0.023	Symmetric
HOMO		-0.323	Anti-symmetric

The HOMO of the transition state is anti-symmetric and the lUMO is symmetric. The HOMO is formed from the overlap of the anti-symmetric HOMO on cis-butadiene and the anti-symmetric lUMO on ethylene so it is expected that it would be anti-symmetric. MO theory states that only MO's with the same symmetry can overlap and in this case the cis-butadiene HOMO and the ethylene LUMO are of the same symmetry and so the reaction is allowed. There is a lot of electron density between cis-butadiene and ethylene in the HOMO indicating that a bond is forming between the two molecules.

The Diels-Alder Reaction of Cyclohexa-1,3-diene and Maleic Anhydride

Another example of a Diels-Alder reaction is that of cyclohea-1,3-diene and maleic anhydride via a stereospecific concerted reaction. There are two possible products; the endo or exo form and their formation depends upon which face of the diene the dienophile attacks. Experimentally only the endo product is formed. This reaction is irreversible and proceeds via kinetic control so we would expect to find that the endo transition state is lower in energy.

Fig 12 - Diels-alder reaction between cyclohexa-1,4-diene and maleic anhydride

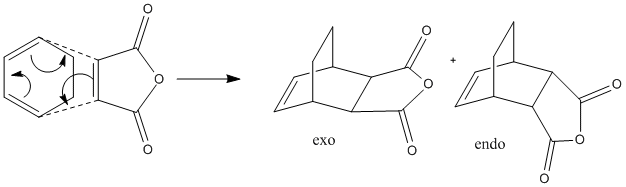Optimising the Transition States

The endo and exo transition states were both optimised by using the frozen coordinate method using the AM1 semi-empirical method and then re-optimised using the DFT/B3LYP/6-31G* method and basis set. Firstly, cyclohexa-1,3-diene and maleic anhydride were separately optimised using the AM1 semi-empirical method. They were then positioned into roughly the shape of the endo transition state. Next this transition state was optimised to a minimum with the C-C bond forming length set to 2.2Å. Then an opt+freq calculation was run with the bonds unfrozen and finally an opt+freq was run using the DFT/B3LYP/6-31G* method and basis set. This was repeated for the exo transition state. published population -endo, published population - exo.

Fig 13- transition states

Table 12- Comparison of Endo and Exo TSfont>

Properties	endo		exo
	Semi-empirical/AM1	DFT/B3LYP/6-31G(d)	Semi-empirical/AM1	DFT/B3LYP/6-31G(d)
Energy (a.u.)	-0.0515	-612.683	-0.0504	-612.679
Imaginary Frequency (cm-1)	-806	-447	-813	-448
C-C Bond Forming Length (Å)	2.16	2.27	2.17	2.29

Changing the method of optimisation to a higher level of theory makes a huge difference to the energy of the transition state. With the B3LYP/6-31G* method giving much more stabilised transition states. As expected the calculated energy for the endo transition state was lower than for the exo transition state (by 2.51 kcal/mol). This may well be to the increased steric repulsion in the exo transition state between the carbonyl oxygen atoms and the hydrogen atoms of cylco-1,3-diene. The partly formed C-C distance is slightly larger in the exo form but the difference is small. These distance are longer than a typical C-C bond length but shorter than the distance of two carbon Van der Waals radii. This implies that that these carbons are close enough to share electron density and so are in the process of forming a bond. There was only one negative frequency detected in the calculations indicating that the optimised structures were in fact transition states. This vibration shows that the reaction proceeds in a synchronous manner as is expected for the concerted Diels-Alder reaction. The lowest positive frequency is 136 cm^-1 and shows no evidence of the concerted reaction mechanism.

The Molecular Orbitals

Table 12 shows that the endo transition structure is lower in energy than the exo structure. This is partly due to increased sterics in the exo structure and partly due to secondary orbital overlap in the endo structure. This secondary orbital overlap occurs between the (O=C)-O-(C=O) fragment and the partly formed C=C double bond. In the exo structure the two reacting molecules are not orientated correctly to allow this secondary orbital overlap to occur. This could be why the C-C bond forming distance is 0.01Å shorter in the endo transition state. Fig 14 shows that in the exo transition state only the primary orbital overlap (that leads to new C-C σ bonds) is possible whereas in the endo transition state there is a secondary orbital overlap besides the primary one. This does not lead to another set of bonds but does stabilise this transition state relative to the exo structure.

Fig 14 - the primary and secondary orbital overlap

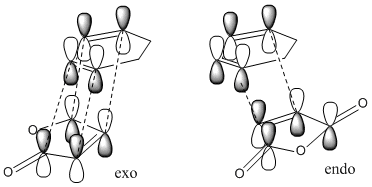If this secondary orbital effect is indeed the reason that the endo structure is lower in energy we should be able to see evidence of it in the molecular orbitals of the transition states.

Table 13 - Frontier Orbitals of the transition state

Molecular Orbital	endo			exo
		Energy (a.u.)	Symmetry		Energy (a.u.)	Symmetry
LUMO		-0.067	Anti-Symmetric		-0.078	Anti-Symmetric
HOMO		-0.242	Anti-symmetric		-0.242	Anti-symmetric
HOMO-1		-0.266	Symmetric		-0.263	Symmetric

The HOMO and LUMO in both the endo and exo transition states are both anit-symmetric to the plane of symmetry. We can see from table 13 that the HOMO orbitals in both the exo and the endo structures have considerable amounts of electron density between the carbons that are in the process of forming C-C σ bonds. In the LUMO structures the orbitals on the diene are out of phase with the orbitals on the dienophile. Unfortunately the HOMO of the endo structure does not show the secondary orbital interaction and we see a nodal plane instead. This is most probably because of the level of theory used in calculating the MO's. Varying the method and basis set varies the appearance of the orbitals. In this case, it is in fact the HOMO-1 that shows evidence of the secondary orbital overlap with MO's between the (O=C)-O-(C=O) fragment and the partly formed C=C bond being in phase.

Conclusion

Using only computational methods we have been able to predict and explain how reactions behave by modelling the transition states. The Cope Rearrangement and the Diels-Alder reaction have been investigated and the outcomes of the reactions have been predicted by calculating the relative energies of various transition states. There are several different methods for optimising transition states but in all of them there is a balance between using a level of theory that is accurate enough but does not take too long. There were a few limitations, for example the HOMO of the endo transition state in the reaction of cyclohexa-1,3-diene with maleic anhydride did not show evidence of the expected secondary orbital overlap effect. Also these calculations did not take solvent effects into account. Despite these limitations, overall these computational methods are very useful in predicting the outcome of chemical reactions.