Rep:Mod:eb108m1
Module 1: The basic techniques of molecular mechanics and semi-empirical molecular orbital methods for the structural and spectroscopic evaluations
Introduction and Aims
The aim of this module is to attempt to illustrate the the uses of molecular modelling, not only to rationalise the outcomes of reactions but also to predict useful modifications and new types of reactions. Two different modelling techniques will be used: molecular mechanics methods MM2 and MMFF94 and the semi-empirical molecular orbitals method MOPAC PM6.
Modelling Using Molecular Mechanics
Hydrogenation of a Cyclopentadiene Dimer
Dimerisation of cyclopentadiene
Cyclopentadiene is the precursor to the protonated cyclopentadienyl ligand which has many applications in organometallic chemistry, such as the creation of ferrocene. At room temperature cyclopentadiene dimerises over a matter of hours in a [4π+2π] Diels-Alder reaction to give either the exo or the endo dimer with cyclopentadiene acting as both the diene and the dienophile. This dimer can then be "cracked" by heating into the two monomers. Experimentally it is found that the endo dimer is the favoured product as is usual for Diels-Alder reactions. This is due to kinetic control over the reaction whereby the HOMO on the dienophile overlaps most favourably with the LUMO of the diene in the endo position, an example of a secondary orbital interaction. [1]This stabilises the transition state of the endo product relative to the transition state of the exo product and hence lowering the activation energy.
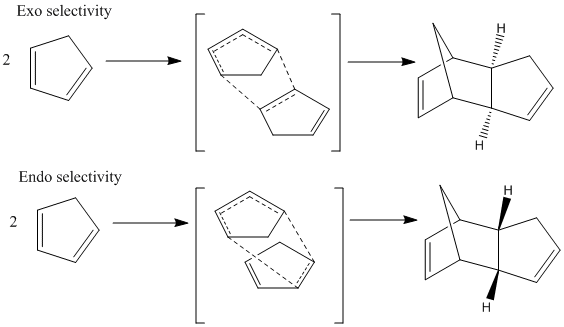 |
Using ChemBio3D Ultra to optimise the structures using the MM2 force field, the stabilisation energies of the products can be estimated. Ideally the energy of the transition states should also be investigated but this is not possible using molecular mechanics. Using this method we can investigate whether this reaction does indeed proceed via kinetic control. Individual contributions to the overall energy can also be analysed.
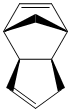 |
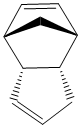 |
| Energy Type | Exo Product Energy / kcal mol-1 | Endo Product Energy / kcal mol-1 |
|---|---|---|
| Stretch | 1.2923 | 1.2454 |
| Bend | 20.5870 | 20.8603 |
| Stretch-Bend | -0.8413 | -0.8320 |
| Torsion | 7.6715 | 9.5039 |
| Non 1,4 VDW | -1.4358 | -1.5083 |
| 1,4 VDW | 4.2320 | 4.3012 |
| Dipole/Dipole | 0.3773 | 0.4448 |
| Total | 31.8817 | 34.0135 |
It can be seen that the energy of the exo form is 2.1318 kcal mol-1 lower than the energy of the endo form and hence is the more thermodynamically stable structure,this being mainly due to the difference in torsional energies (1.8324mol-1). However, experimentally the endo form is predominantly formed in the dimerisation and so it can be deduced that this reaction does indeed proceed via kinetic control.
Hydrogenation
This dimer contains two double bonds - one norboreneC=C bond and one cyclopenteneC=C bond. It is possible to hydrogenate this dimer, although only one double bond will be hydrogenated unless the reaction is left for a very long time. This partial hydrogenation can give two possible products (product 1 and product 2 shown below)
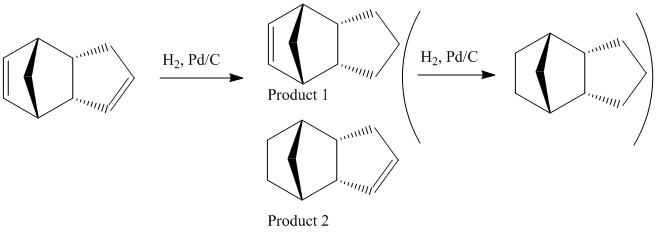 |
As before, the structures can be optimised to give the relative thermodynamic energies.
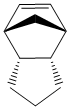 |
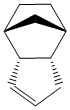 |
| Energy Type | Product 1 / kcal mol-1 | Product 2 / kcal mol-1 |
|---|---|---|
| Stretch | 1.2279 | 1.0963 |
| Bend | 18.6932 | 14.5074 |
| Stretch-Bend | -0.7442 | -0.5493 |
| Torsion | 12.8241 | 12.4972 |
| Non 1,4 VDW | -1.3366 | -1.0507 |
| 1,4 VDW | 6.0390 | 4.5124 |
| Dipole/Dipole | 0.1632 | 0.1407 |
| Total | 36.8666 | 31.1540 |
The energy of product 1 is 5.7126 kcal mol-1 higher than the energy of product 2 hence showing that if this reaction proceeds via thermodynamic control then hydrogenating the double bond from the bridged ring system is thermodynamically more favourable than hydrogenating the double bond in the cyclopentene. Looking at the individual contributions to the energy it can be seen that biggest difference between the two products is in the bend energy (4.1861 kcal mol-1) although there is also a small difference in the Van der Waals energy (1.5266 kcal mol-1). The other contributions to the energy are very similar. Assuming that this reaction proceeds via thermodynamic control then product 2 is the most favourable. This is because the norbornene C=C bond is more strained than the cyclopentene C=C bond.
Stereochemistry of Nucleophilic additions to pyridinium ring (NAD+ analogue)
Pyridium species (containing a pyridine ring) can be alkylated on the 4 position of the pyridine ring using alkylating reagents such as grignard or organolithium reagents. In this section we are looking at the nucleophilic attack of two Nicotinamide adenine dinucleotidederivatives. N-methyl pyridoxazepinone is the optically active derivative of prolinol and reacts with MeMgI to give molecule b in the mechanism shown below.
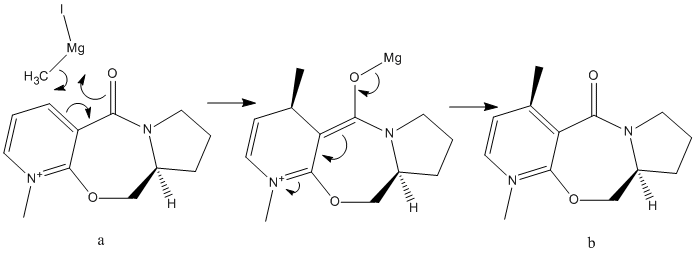 |
This reaction is highly regio- and stereoselective which is due to coordination between the electropositive magnesium on the Grignard reactant and then electronegative carbonyl oxygen[2] forming a magnesium enolate intermediate. This leads to the grignard attacking from the top face of the ring. The stereocentre on molecule a is retained during the reaction so that molecule b has two stereocentres.
The structure of molecule a was optimised using molecular mechanics modelling to investigate the likelihood of the reaction proceeding via the suggested mechanism shown above. The dihedral angle between the carbonyl and the aromatic ring was measured to verify the proposed mechanism.
| Configuration | Structure | Energy / kcal mol-1 | Dihedral angle |
|---|---|---|---|
| 1 | 43.1387 | 11 | |
| 2 | 45.3500 | 20 | |
| 3 | 35.1385 | 11 | |
| 4 | 42.0605 | 10 |
The various optimisations show that whilst the dihedral angle between the carbonyl and the plane of the aromatic system varies between 10o and 20o it is at all times above the plane of the ring. This shows that the above mechanism is correct and that the magnesium chelates to the oxygen and so attacks the ring from above. It is unfortunately not possible to model molecule a including the grignard reagent chelated to the oxygen as the MM2 calculation cannot model transition states. Other calculation methods such as the Gaussian or MOPAC methods, would need to be used to model the transition state.
Another reaction involving a pyridinium species is the attack of aniline onto N-methylquinolium (mechanism shown below) which also proceeds via regio- and stereoselectivity. In this case, the carbonyl repels the aniline molecule which attacks from the opposite side of the ring that the carbonyl is orientated[3]. This leads to diastereselectivity in the reaction.
 |
As before the structure of molecule c can be modelled to see whether aniline attacks above or below the ring and whether it chelates with the oxygen as with the previous reaction.
| Configuration | Structure | Energy / kcal mol-1 | Dihedral angle |
|---|---|---|---|
| 1 | 62.7363 | -20 | |
| 2 | 63.5351 | -19 | |
| 3 | 64.0232 | -24 | |
| 4 | 284.9746 | 46 |
From this we can see that when the energy of the optimised structure is reasonable (i.e. not configuration 4) the dihedral angle is around 20o and is negative. This means that the carbonyl is orientated on the bottom side of the ring and the suggested mechanism for this reaction is indeed correct - the aniline attacks from the opposite face to the carbonyl. This is as expected as aniline and the carbonyl group are both lewis acids.
It is necessary to remember when studying these reactions that the large ring size in molecules a and c (seven-membered ring) means that there are a fairly wide variety of conformations that these molecules can occupy. This is why a variety of configurations were tried out to try and get a feel for the range of conformations that these molecules can have. It may well be that a slightly lower energy state exists that hasn't been modelled above. These models could be improved by studying the transition states in both reactions and by using a more advanced method of calculation. MM2 accounts for sterics and lone pairs but methods such as MOPAC PM6 or Gaussian DFT are molecular orbital models and are more accurate.
Stereochemistry and Reactivity of an Intermediate in the synthesis of Taxol
Atropisomerism occurs when a molecule that would otherwise be able to freely rotate is constrained so that at room temperature it has a number of stable configurations with a sufficiently large kinetic energy barrier prevented them from readily inter-converting. An example of this is an intermediate from the production of taxol that exists as one of two atropisomers (molecules e and f shown below). The carbonyl is either pointing upwards or downwards and both configurations are stable[4]. Molecule e isomerises to f when left to stand[5].
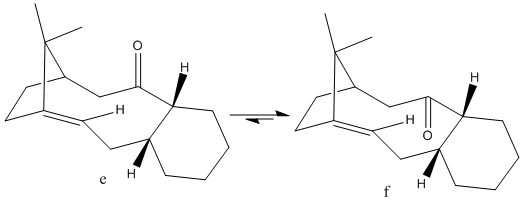 |
This intermediate has increased rigidity due to the bridgehead alkene which is the origin of the two atropisomers. It is slow to hydrogenate - as it is an example of a hyperstable alkene and so is less strained than its hydrogenated alkane[6]. Upon hydrogenation the increased strain destabilizes the molecule more than the bond formation can stabilize the molecule. This can be rationalised by thinking about the frontier orbitals; a twisted alkene has reduced π overlap which raises the HOMO energy and lowers the LUMO energy. At a twist angle 90o the HOMO and LUMO are degenerate (D2d symmetry). The amount of strain on the alkene directly correlates with the reactivity.[6] The two isomers can be modelled using the MM2 and MMFF92 calculations.
| Energy kcal mol-1 | |||
|---|---|---|---|
| Stretch | 2.6595 | 2.5351 | 4.8600 |
| Bend | 15.8127 | 10.7022 | 25.3814 |
| Stretch-Bend | 0.3833 | -0.3181 | 1.1813 |
| Torsion | 18.3378 | 19.7589 | 20.5513 |
| Non 1,4 VDW | -1.1101 | -1.3946 | 1.3147 |
| 1,4 VDW | 12.6751 | 12.5548 | 19.1476 |
| Dipole/Dipole | 0.1482 | -0.1815 | 0.000 |
| Total/ MM2 | 48.9065 | 44.2929 | 72.4464 |
| Total/MMFF94 | 70.5392 | 60.5617 | 109.387 |
We can see that energy of isomer f (calculated using MM2) is 44.2929 kcal mol-1 lower than that of isomer e. The greatest difference in the individual components of the energy is in the bend energy (5.1105 kcal mol-1. Although there is also a noticeable difference in the torsion energy it is smaller (1.4211 kcal mol-1). The remaining components of the energy are fairly similar. The energies calculated using the MMFF92 model are significantly higher due to using a different force field but still show the same pattern with the energy of isomer e being higher (by 9.9775 kcal mol-1). When hydrogenated isomer e and f both have the same configuration because the alkene (the component that created the kinetic energy barrier between isomers) has been removed. The energy of the hydrogenated product was higher and as expected the bending energy showed the largest increase as the hydrogenated product is more strained.
Modelling using Semi-empirical molecular orbital theory
In the previous examples the limitations of molecular mechanics theory have been demonstrated. This theory cannot explain secondary orbital effects or calculate the energies of transition states. In the following example the models are minimised using MM2 and MOPAC PM6 and the results compared.
Regioselective addition of dichlorocarbene
The addition of the powerful electrophile, dichlorocarbene to alkenes yields 1,1-dichlorocyclopropane species [7]. When added to 9-chloromethanonenaphthalene the reaction shows excellent π-selectivity with the syn trichloride being the major adduct (72%) [8].
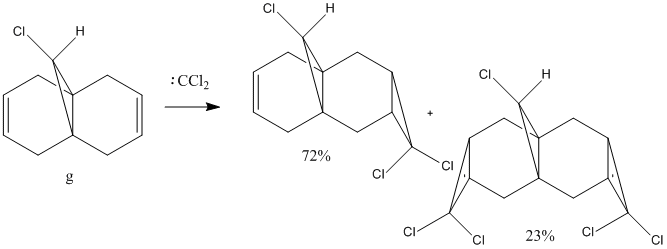 |
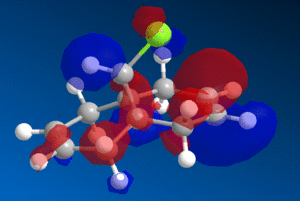
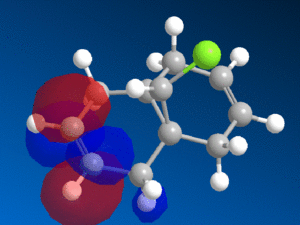
This reactivity is due to the molecular orbitals and so the HOMO and LUMO orbitals (as well as those close to the frontier orbitals) of 9-chloromethanonenaphthalene were modelled using the PM6 method to investigate this reactivity.
| HOMO-1 | HOMO | LUMO | LUMO+1 | LUMO+2 |
 |
 |
 |
 |
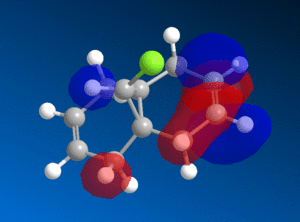 |
We can see from the molecular orbitals that the majority of the electron density is on the syn double bond in the HOMO. This means that the highly electrophilic dichlorocarbene will prefer to attack this electron rich, nucleophilic syn alkene rather that the electron poor anti double bond and so the endo product is favoured. There is a large amount of electron density on the anti alkene in the HOMO-1 layer which is lower in energy and so less reactive. In addition to this there is also a stabilising interaction between the C-Cl σ* orbital in the LUMO+1 and the anti-alkene π orbital HOMO-1 that causes the anti-alkene π orbital to become even lower in energy than the syn-alkene π orbital in the HOMO (see fig 9) [9]. The anti-alkene can react only once the syn-alkene has reacted which is why the di-adduct is also formed as a minor product. Other factors such as sterics have a minimal effect and so looking at the MO's is a good prediction of the selectivity in this reaction.
 |
Vibrational Frequencies
Using the B3LYP/6-31G(d,p) Gaussian geometry optimization and frequency calculation the vibrational frequencies of the molecules were computed and the IR spectrum deduced. The symmetry of the di-alkene is Cs as the cyclohexene rings are planar and so the molecule has one plane of symmetry σh. Defining this molecule as Cs before submitting the job made it run a lot faster. This is not possible to do for the hydrogenated product as the cyclohexane ring has a twist-chair conformation and so there are no symmetry planes and the molecule has C1 symmetry.
| molecule | Syn alkene bond stretch/ cm-1 | Anti alkene bond stretch/ cm-1 | C-Cl bond stretch/ cm-1 |
|---|---|---|---|
| 1757.36 | 1737.09 | 770.90 | |
| 1755.76 | n/a | 779.93 | |
| 1756.28 | 1776.60 | 766.78 | |
| 1756.26 | 1690.36 | 763.83 |
| 9-chloromethanonenapthalene | Hydrogenated product |
 |
 |
The wavenumbers for the C=C stretches are slightly higher than the literature values of 1640-1680 cm-1 suggesting that these double bonds are stronger than the "normal" double bonds.[10]The C-Cl corresponds well to the literature value of 760 cm-1[10]. The differences in the wavenumbers may be due to the fact that frequencies of the bond vibrations were calculated with the bond modelled as a harmonic oscillator whereas in actual case the stretches may be closer to anharmonic.
We can see that the syn C=C bond has a higher wavenumber and so a stronger bond which corresponds well to the theory - the syn bond is more nucleophilic. Upon hydrogenation of the anti C=C bond, the C-Cl wavenumber increases indicating that this bond has increased in strength. This is due to the donation from the anti-alkene π orbital into the C-Cl σ* orbital weakening the C-Cl bond (see fig. 9). The bond stretch of the syn alkene remained roughly constant before and after hydrogenation indicating that this bond has not been affected by the hydrogenation.
The effect of substituents on the anti double bond was investigated by adding an -OH group and then an -SiH3 to see what affect this had on the bond vibrations. The bond stretch for the syn alkene did not change but(as expected) the anti alkene was affected by the substituents. The bond increased in strength upon addition of the -OH group probably due to resonance as oxygen is more electronegative than carbon and the inductive effect would be towards the oxygen. The anti C=C bond decreased in strength when the -SiH3 group was added due to electron donation into the antibonding C=C orbital. In both cases the C-Cl bond decreased in strength, which for the -OH substituted molecule is due to more electrons in the C=C π orbital and hence more electron density in the C-Cl σ* orbital (see fig. 9) weakening the bond.
Structure Based Mini Project using DFT-based Molecular Orbital Methods
Investigating the regiochemistry of the Baeyer-Viliger oxidation
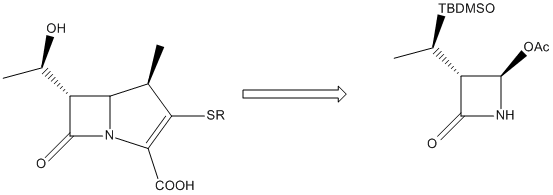 |
The Baeyer-Villiger Oxidation is the oxidative cleavage of ketones to esters or cyclic ketones to lactones where the bond being cleaved is a C-C bond adjacent to the carbonyl. Peracids such as mCPBA (meta-chloroperoxybenzoic acid), peroxyacetic acid or peroxytrifluoroacetic acid are used as reagents. The driving force is the exothermicity of the formation of the C=O bond and the cleavage of the weak O-O bond. This reaction is stereospecific and can be regiospecific. A synthesis of acetoxyazetidinine (a member of the Carbapenem family) has been suggested that involves a Baeyer-Villiger Oxidation as one of the important synthetic steps[11].
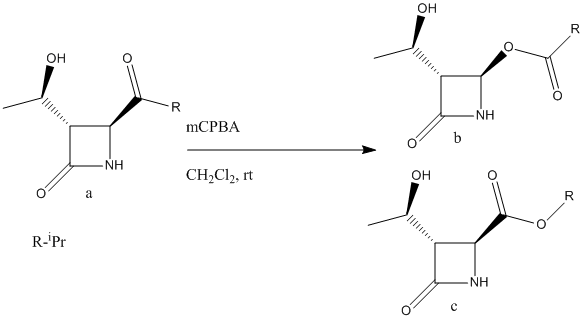 |
There are two possible products from the oxidative cleavage of molecule a (see fig. 12); the desired product, a β-lactam (b) or it's regioisomer (c). In this reaction, the R- group adjacent to the carbonyl is iPr and the reaction gives a racemic mixture of the two regioisomers (52% of b and 48% of c). In contrast, if the R- group is a phenyl then 100% of molecule b is formed and if the R- group is tbutyl then the reaction proceeds with a total inversion of regiochemistry and 100% of molecule c is formed. Clearly the nature of the R- group has a major impact on the regiochemistry of the reaction and the key to understanding this is to look at the two competing reaction mechanisms.
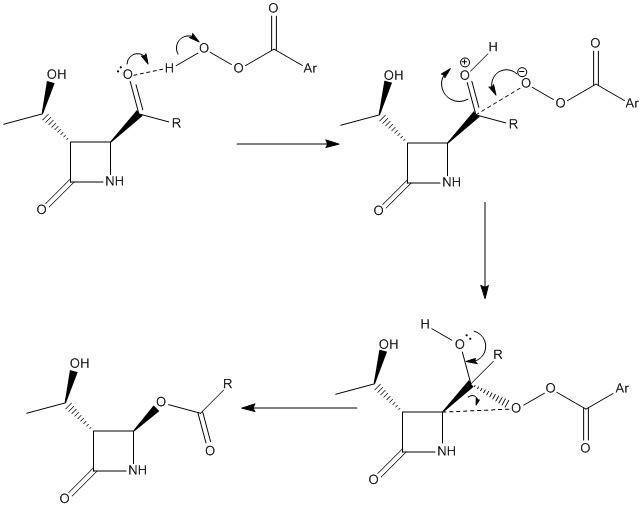
Fig 13 – the two possible mechanisms for the Baeyer-Villiger reaction [12]| Mechanism 1- to form b | Mechanism 2- to form c |
 |
 |
Both the mechanisms proceed via a Criegee intermediatewhich forms the final product via the overlap of anti-periplanar bonds (the app relationships are shown in fig 14). In both intermediates the app relationships are between the lone pair on the oxygen and σ* C-C and between the σ C-C bond and the σ* O-O bond.[12] 1)no-->σ* C-C(app) 2)σ* C-C(app)-->σ* O-O
Fig 14 – the Creigee Intermediates| Intermediate b | Intermediate c |
 |
 |
These app relationships allow a [1,2]-sigmatropic rearrangement to take place which leads to the final product. A [1,2]-sigmatropic rearrangement takes place when an electron deficient/cationic centre is formed next to a group capable of migration.[13] In the Criegee intermediate either the R- group or the carbon adjecent to the -OH migrates towards the electron deficient oxygen. Therefore, the nature of the R- group plays an important role in which part of the intermediate is the migrating centre. The ease of migrations is dependant upon the particular reaction and conditions although in general the groups that can stabilise a positive charge are more prone to migrating. Hence, tBu, which is a tertiary alkyl,is an excellent migrating group as it is very good at stabilising positive charge. This explains why 100% of product c is formed when tBu is the R- group. In this reaction iPr, a secondary alkyl,is the R- group which, whilst it can stabilise a positive charge, does not do so as well as a tBu group leading to a mixture of regioisomers formed. Changing the R- group to a phenyl is interesting because this does not readily migrate despite the fact that it can stabilise a positive charge better than iPr. It may well be that it is too bulky and that sterics prevent it from migrating. The other factor that is crucial to migration is correct orbital overlap which is one the reasons why cyclopropyl does not migrate - the C-C orbitals have sp2 character. The reduced number of C-H bonds involved in the hyperconjugate stabilisation also plays a part. To summarise, tBu as the R- group gives 100% of the undesired product c whereas Ph and cPr give 100% gives 100% of the desired product b.[14] Using iPr, as in this reaction, gives a mixture of the two products and so it becomes especially important to differentiate between them.
NMR
NMR is a useful tool for differentiating between isomers, especially regioisomers as the chemical shifts can be very different. In this calculation molecules b and c were optimised using the MM2, MOPAC and then Gaussian DFT method. The NMR shifts were then calculated and compared to experimental data.
Fig 15 – the two products| Molecule b | Molecule c |
 |
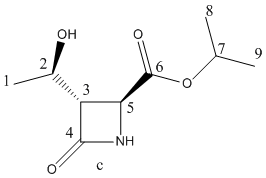 |
| Carbon | δ(calc)/ppm | δ(calc)-corrected/ppm | δ (exp)/ ppm |
|---|---|---|---|
| 6 | 174.23 | 179.46 | 177.6 |
| 4 | 157.90 | 163.78 | 167.2 |
| 5 | 77.88 | 77.88 | 75.9 |
| 2 | 66.44 | 66.49 | 65.2 |
| 3 | 64.88 | 64.88 | 63.9 |
| 7 | 35.87 | 35.87 | 34.0 |
| 1 | 22.95 | 22.95 | 21.3 |
| 8 | 21.42 | 21.42 | 18.9 |
| 9 | 19.59 | 19.59 | 18.8 |
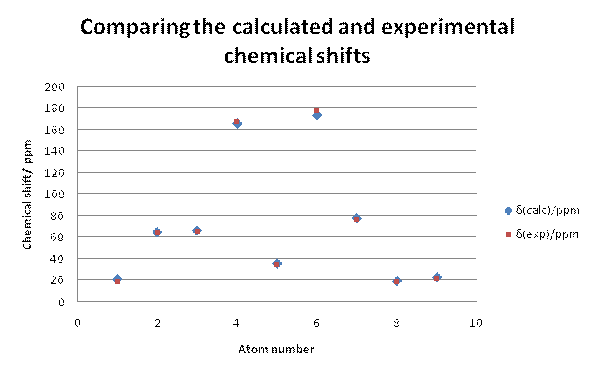
Firstly the 13C NMR for the desired product b was modelled and it can be seen from the graph below that the calculated NMR data fitted well with the experimental NMR data. In almost all cases, the calculated chemical shifts were higher than the experimental chemical shifts by about 2ppm or slightly less. This suggests that there is a systematic error in the calculation that leads to a slight overestimate of the chemical shift. The data points for C-6and C-4 had to be corrected using the equation xcorr=0.96xcalc+12.2 [15] as the predicted chemical shift breaks down somewhat for carbonyls when using the Gaussian DFT model. Despite the correction, the chemical shifts for C-4and C-3 are about 2.5-3ppms out from the experimental data. The carbons that could show the largest deviation from the experimental NMR's would be C-7, C-8 and C-9 because there are possible rotamers around these carbons. However, the deviation from the experimental shifts for these carbons is of a similar size to the deviations from the experimental shifts for the more constrained carbon centres indicating that the modelled stereochemistry around the C7-9 carbons is close to the experimental stereochemistry.
Fig 16 – comparing the experimental and calculated chemical shifts for b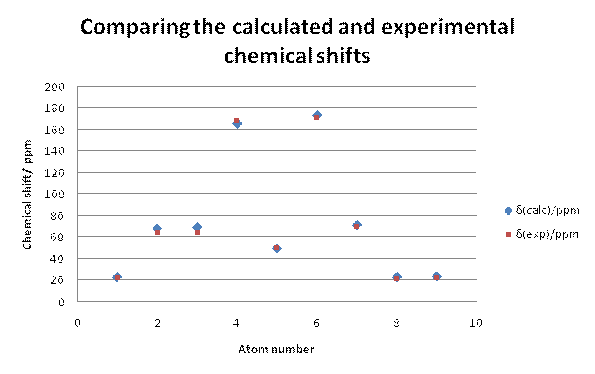 |
| Carbon | δ(calc)/ppm | δ(calc)-corrected/ppm | δ (exp)/ ppm |
|---|---|---|---|
| 6 | 168.12 | 173.59 | 170.8 |
| 4 | 160.15 | 165.94 | 168.3 |
| 7 | 71.31 | 71.31 | 69.7 |
| 3 | 69.29 | 69.29 | 64.5 |
| 2 | 67.96 | 67.96 | 64.0 |
| 5 | 49.43 | 49.43 | 50.0 |
| 9 | 23.37 | 23.37 | 21.9 |
| 1 | 22.88 | 22.88 | 21.8 |
| 8 | 22.78 | 22.78 | 21.3 |
Next, the 13C NMR for the undesired product (c)was modelled. Most of the calculated chemical shifts corresponded well with the experimental data but C-2 was out by almost 4 ppm indicating that the modelled stereochemistry at this carbon centre does not match so well with the experimental stereochemistry. The -OH group is shown in the literature to be sticking out from the plane of the paper but the angle of the -OH group with relationship to the plane is not indicated. This angle on the model is most likely slightly different to the experimental molecule leading to this difference in chemical shift. Apart from C-2 the calculated chemical shifts are less than 3 ppm from the experimental values.
Comparing the NMR data for products b and c can allow us to distinguish between the isomers. Some of the carbons show small differences in the chemical shifts, for instance the chemical shifts for C-1, C-8 and C-9 are all higher in product c (C-9 by almost 4ppm). Also C-3 is higher in product c by about 4.5ppm. However, the largest differences occur in the carbons that are adjacent to the ester group. The chemical shift for C-5 is 28.4ppm higher in product c, C-7 is 35.4 ppm higher in product b. This is a very large difference and and is very obviously explained by the differing positions of the ester in the products. The carbon adjacent to the carbonyl is lower in energy than the carbon adjacent to the ether in both products.
 |
IR
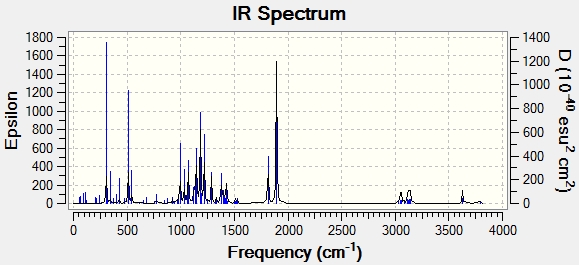
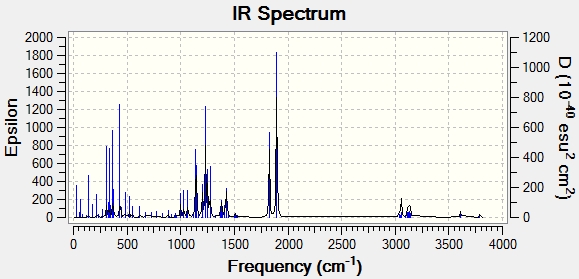
Another technique that can be used to distinguish the two isomers is Infra-Red spectroscopy. Using the same techniques as before, the IR spectra for products b and c were modelled and the results compared to the experimental results. However the calculated IR frequencies did not match well with the experimental results. The frequencies were overestimated by a large amount and in fact, showed very little difference between the regioisomers. It can be concluded that IR is a good experimental technique to distinguish between these isomers but a bad computational technique for distinguishing between them.
| Bond type | Product b(calc) | Product b(exp) | Product c(calc) | Product c(exp) |
|---|---|---|---|---|
| C=O (1) | 1814 | 1740 | 1825 | 1721 |
| C=O (2) | 1894 | 1783 | 1895 | 1749 |
| N-H | 3628 | 3330 | 3611 | 3341 |
| product b | product c |
 |
 |
Conclusion
In conclusion, molecular modelling is a very useful technique for predicting reactions and for distinguishing isomers but it has many limitations. For example the MM2 model could not predict the energies of transition states and so could only predict favourable thermodynamic products. Also, the Gaussian DFT model overestimated the IR frequencies in the Mini project. However, many of the results predicted by the computational models were very close to experimental values and when combined with a certain amount of chemical intuition were very good at predicting the behaviour of molecules during reactions.
References
- ↑ P. Caramella, P. Quadrelli, L. Toma. J. Am. Chem. Soc. 124, 7, 2002[1]
- ↑ A.G. Shultz, L. Flood et al. J. Org. Chem., 1986, 51, 838 [2]
- ↑ S. Leleu, C. Papamicael, F. Marsais, G. Dupas, V. Levacher, Tetrahedron: Asymmetry, 2004, 15, 3919-3928. DOI:10.1016/j.tetasy.2004.11.004
- ↑ S. W. Elmore and L. Paquette, Tetrahedron Letters, 1991, 319[3]
- ↑ L. A. Paquette. Stereocontrolled Construction of Complex Cyclic Ketones via Oxy-Cope Rearrangement. Angew. Chem. Int. Ed. Engl. 29 (I990) 609-626[4]
- ↑ 6.0 6.1 W. F. Maier, P. R. Schleyer, J. Am. Chem. Soc., 1981, 103, 1891-1900. DOI:10.1021/ja00398a003
- ↑ A. Spivey, An Introduction to Reaction Stereoelectronics, 3rd Year, Lecture 5
- ↑ B. Halton, S. G. G. Russell. J. Org. Chem., Vol.56,No.19, 1991[5]
- ↑ B. Halton, R. Boese and H. S. Rzepa., J. Chem. Soc., Perkin Trans 2, 1992, 447[6]
- ↑ 10.0 10.1 IR Correlation Table[7]
- ↑ M. Laurent, M. Ceresiat, J. Marchand-Brynaert, J. Org. Chem., 2004,69,p3194-3197 [8]
- ↑ Alan Spivey Year Three Lecture notes, lecture 5, page 7 [9]
- ↑ Alan Spivey Year Three Lecture notes, lecture 4, page 6 [10]
- ↑ M. Laurent, M. Ceresiat, J. Marchand-Brynaert, J. Org. Chem., 2004,69,p3194-3197 [11]
- ↑ Rezpa, Third Year Computational Labs, Module 1[12]
