Rep:Mod:dutMMP
NH3 Key Information
Molecule Name
This is a a NH3 molecule. Also known as Ammonia.
Calculation Method
RB3LYP
Basis Set
6-31G(d,p)
Final Energy E(RB3LYP) (au)
-56.55776873
Molecule Point Group
C3v
Item Table Info
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
[Figure 1] Optimized NH3 Molecule |
View the LOG file for the Optimized NH3 Molecule here
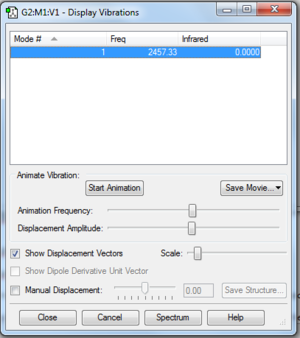
NH3 Vibrational Analysis Output

it can be seen in the "Display Vibrations" screenshot image above that none of the frequency values are negative, which may have been the case if the molecule was not optimized.
NH3 Vibrational Analysis Question Answers
- How many modes did I expect from the 3N-6 rule?
- The Number of atoms present in Ammonia is 4.
- ∴ N = 4
- ∴ 3(4) - 6 = 6
- ∴ I would expect 6 vibrational modes according to the 3N-6 Rule, which corresponds to the number of vibrational modes that were displayed.
- Which modes are degenerate (ie have the same energy)?
- According to the Figure 2, there are 2 pairs of modes that are degenerate; 2 & 3 are degenerate, 5 & 6 are also degenerate.
- As far as which modes are "bending" vibrations and which are "bond stretch" vibrations:
- Bend: 1, 2, 3
- Stretch: 4, 5, 6
- In terms of which modes are highly symmetric:
- Mode 1 (symmetric bend)
- Mode 4 (symmetric stretch)
- One mode is known as the "umbrella" mode, which one is this?
- "Umbrella Mode" is a reference to a form of vibration which resembles the opening and closing motion of an umbrella. In the case of the NH3, this mode is specifically the symmetric bend mode which, as stated above, is shown by mode 1.
- How many bands would you expect to see in an experimental spectrum of gaseous ammonia?
- There are 6 vibrational modes, however since within those 6 modes there are 2 pairs of degenerate modes, the total number of distinct energy levels will be 4. This therefore means that on an experimental spectra, I would expect to see 4 bands, however when I take into consideration the infrared magnitude of 2 of these bands(extremely small), I would thus expect to only see 2 bands on the spectrum:
- 1089.54 (Mode 1)
- 1693.95 (Mode 2 & 3)
*All frequencies are in the units cm-1*
- There are 6 vibrational modes, however since within those 6 modes there are 2 pairs of degenerate modes, the total number of distinct energy levels will be 4. This therefore means that on an experimental spectra, I would expect to see 4 bands, however when I take into consideration the infrared magnitude of 2 of these bands(extremely small), I would thus expect to only see 2 bands on the spectrum:
NH3 Charges on Atoms

It can be seen from the image that the charges present are as follows:
Atom Charge
Nitrogen -1.125
Hydrogen 0.375
These results are as expected. My reason being that Nitrogen is more electronegative than Hydrogen and so would draw the electron density closer towards it than the Hydrogen atoms, thus having a negative charge and the hydrogen atoms having a positive charge.
N2 Key Information
Molecule Name
This is a a N2 molecule.
Calculation Method
RB3LYP
Basis Set
6-31G(d,p)
Final Energy E(RB3LYP) (au)
-109.52412868
Molecule Point Group
D∞h
Item Table Info
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
[Figure 4] Optimized N2 Molecule |
View the LOG file for the Optimized N2 Molecule here
N2 Vibrational Analysis Output
it can be seen in the "Display Vibrations" screenshot image above that the frequency value of the mode is confirmed to be positive.
N2 Charges on Atoms

It can be seen from the image that the relative charges on each N atom is zero, since it is a homonuclear diatomic molecule with equal electronegativity values and so equal distribution of charge.
H2 Key Information
Molecule Name
This is a a H2 / Hydrogen molecule.
Calculation Method
RB3LYP
Basis Set
6-31G(d,p)
Final Energy E(RB3LYP) (au)
-1.17853936
Molecule Point Group
D∞h
Item Table Info
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
[Figure 6] Optimized H2 Molecule |
View the LOG file for the Optimized H2 Molecule here
H2 Vibrational Analysis Output

it can be seen in the "Display Vibrations" screenshot image above that the frequency value of the mode is confirmed to be positive, which is indicative of an optimized molecule.
H2 Charges on Atoms

It can be seen from the image, like that of the Nitrogen atoms in N2, that the relative charges on each H atom is zero. This is because it is a homonuclear diatomic molecule with equal electronegativity values and so equal distribution of charge.
Haber-Bosch process reaction energies**
H2 Reaction Energy Calculations
The following are calculations to work out the overall reaction energy change for the Haber-Bosch process (N2 + 3H2 → 2NH3).
**The Energies in these calculations are in "au" unless otherwise stated.
- E(NH3) = -56.55776873
- 2 * E(NH3) = 2 * -56.55776873
- E(N2) = -109.52412868
- E(H2) = -1.17853936
- 3 * E(H2) = 3 * -1.17853936
- ΔE = 2 * E(NH3) - [E(N2) + 3 * E(H2)] = -113.11553746 - [(-109.52412868) + (-3.53561808)] = -0.0557907 au
- -0.0557907 au = -146.47848285 kJ mol-1
Energy for converting Hydrogen and Nitrogen gas into Ammonia gas
- -146.48 kJ mol-1
N2 + H2/NH3 Reactants/Products: 'Which is more stable' Evaluation
- The enthalpy change of the reaction is negative (i.e exothermic). This implies that the gaseous reactants were higher in energy than the ammonia product. Therefore we can deduce that the Ammonia product is more stable than the gaseous Reactants. (2NH3 more stable than N2 + 3H2)
ClF3 Key Information
Molecule Name
This is a ClF3 molecule. Also known as Chlorine trifluoride.
Calculation Method
RB3LYP
Basis Set
6-31G(d,p)
Final Energy E(RB3LYP) (au)
-759.46531674
Molecule Point Group
Cs
Item Table Info
Item Value Threshold Converged? Maximum Force 0.000132 0.000450 YES RMS Force 0.000093 0.000300 YES Maximum Displacement 0.000677 0.001800 YES RMS Displacement 0.000417 0.001200 YES
[Figure 8] Optimized ClF3 Molecule |
View the LOG file for the Optimized ClF3 Molecule here
ClF3 Vibrational Analysis Output

it can be seen in the "Display Vibrations" screenshot image above that none of the frequency values are negative, which may have been the case if the molecule was not optimized.
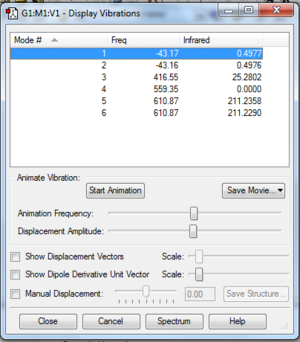
ClF3 Vibrational Analysis Question Answers
- The Number of atoms present in Chlorine trifluoride is 4.
- ∴ N = 4
- ∴ 3(4) - 6 = 6
- ∴ I would expect 6 vibrational modes according to the 3N-6 Rule, which corresponds to the number of vibrational modes that were displayed.
- According to Figure 9, there are no modes that are degenerate - I have concluded this from the fact that all of the 6 vibrations listed are of different frequencies. It should be noted though that there are 2 frequencies that are extremely close in magnitude and would likely show up as one peak on a spectrum.
How many modes did I expect from the 3N-6 rule?
Which modes are degenerate (ie have the same energy)?
As far as which modes are "bending" vibrations and which are "bond stretch" vibrations [From observing the gaussview animations and combining those observations with the knowledge that stretches tend to be higher energy than bends]:
Mode # Vibration Type
1 Symmetric Bend
2 Symmetric Bend
3 Asymmetric Bend
4 Symmetric Stretch
5 Symmetric Stretch
6 Asymmetric Stretch
How many bands would you expect to see in an experimental spectrum of gaseous Chorine trifluoride?
- There are 6 vibrational modes and no degenerate modes; therefore I would, based on solely that, expect to see 6 bands on an experimental spectrum - corresponding to the frequencies of the different modes. However, upon examination of the Infrared values from the Vibrational analysis results [Figure 9], it becomes apparent that two of them are so small in magnitude(Modes 3 & 4) that it is highly doubtful that they would be seen on an experimental spectrum. Taking this into consideration and also the fact that Mode 1 and mode 2 are extremely close together in frequency but not quite degenerate, I would expect to see 3 bands on an experimental spectrum.
ClF3 Charges on Atoms

It can be seen from the image that the charges present are as follows:
Atom Charge
Chlorine[1 at this charge] 1.224
Fluorine[2 at this charge] -0.454
Fluorine[1 at this charge] -0.316
These charge results are as expected. My reason being that Fluorine is more electronegative than Chlorine and so the Fluorine atoms would draw the electron density more strongly towards them than the Chlorine atom, thus the Fluorine atoms each have a slightly negative charge and the Chlorine atom has a positive charge. Due to the symmetry of the molecule, the molecule is neutrally charged overall.
Comments on ClF3 Optimization Process
The initial ClF3 optimization that I ran did not fully optimize, despite the fact that all of the variables in the optimized item table info registered "converged" as can be seen in the table [Fig ###].
Item Value Threshold Converged? Maximum Force 0.000011 0.000450 YES RMS Force 0.000007 0.000300 YES Maximum Displacement 0.000049 0.001800 YES RMS Displacement 0.000032 0.001200 YES
[Figure 10] Result of Initial Attempt to optimize ClF3 |
View the LOG file for the result of the Initial Optimization attempt of ClF3 Molecule here
The lack of full optimization was shown to me through the Negative frequency values when I looked in the Vibration Modes section. Initially I thought this was due to wrong settings on the calculation page, however I double checked that and it was ok. I was able to solve the negative frequency values problem through first constructing the molecule as CF6 and then deleting the extra Fluorine Atoms before then running the optimization. I decided to do this because according to the literature, the optimized structure of ClF3 is T-shaped.
Comparison between First Optimization attempt and Second/Final Optimization
Attempt Final Energy Value(au) Point Group Molecular Geometry 1 -759.44149573 D3h Trigonal Planar 2 -759.46531674 CS T-Shaped
ClF3 AO/MO Exploration

The electron density of this particular molecular orbital is concentrated around the Cl Atom.
Based on the shape of it and the relative ionization energy level of -9.58, this is a S bonding orbital (Most likely a 1s bonding orbital).
One of the reasons for this determination is the lack of nodal planes in the orbital model, which would be indicative of it being an anti-bonding orbital.

This particular orbital is the LUMO of the molecule. One thing that is immediately striking about it is the number of Nodal planes that exist in this particular orbital model. This to me is indicative of the fact that the regions that can be seen on the "outside" part of the molecule. This to me is a sign that those are "antibonding" lobes of the molecular orbital. Reason being is that when those particular regions are occupied by a sufficient amount of electron density, that will cause the bond on the inside to be pulled apart.

This is the HOMO of the molecule. This particular orbital contains the highest energy electrons of the molecule, and also the electrons of the molecule that are most easy to ionise, as shown by the relative "ionisability" value of -0.33 which is the least negative of any occupied orbital in the molecule.

Here are some P orbitals of the Chlorine atom.

There is a lack of nodal planes crossing any of the bonds in this molecular orbital, and also most of the electron density is distributed between the bonding atoms as opposed to on the outside of them. That is distributed across the whole structure of the atom. The relative energy level of the electrons in this particular molecular orbital is -1.28. The electrons here, in comparison to the S bonding orbital shown in Figure 12 would require less energy to be supplied suffient energy for ionisation.
