Rep:Mod:dt2315TS

Introduction

Gaussian was used to study three Diels-Alder reactions (DA) and an electrocylic process using the GaussView interface and different theory levels.

Gaussian

Shortly, Gaussian is a computational chemistry programme that works with the positions of atoms and two main approximations. In the Born-Oppenheimer approximation, the slow, heavy nuclei are treated classically and the electrons are treated quantum mechanically. In the second approximation, the electrons are considered to be independent from each other and the wavefunction for the average interaction is calculated as a linear combination of atomic orbitals. A potential energy surface (PES) arises as a consequence of the BO approximation in which the potential of nuclear motion is shown when nuclei are allowed to change position. Although the PES is often reduced to 2D to be visualised, there actually are 3N - 6 dimensions or degrees of freedom. By looking at how the gradient of the potential energy varies in the PES, one can gain information regarding the energy of different geometries.

Nf710 (talk) 12:44, 16 January 2018 (UTC) It is mainly the potential of the electrons WRT the new positon of the nuclei which gives rise to a new point on the electronic PES.

Minimum and TS on a PES

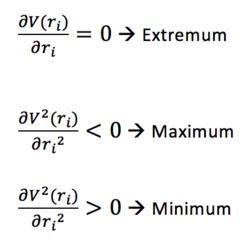
With one dimension, a 0 first derivative gives a maximum or a minimum. In order to differentiate between the two, the sign of the second derivative is needed. A positive one corresponds to a minimum, a negative one corresponds to a maximum and a zero second derivative corresponds to an inflexion point. Similarly, in i dimensions, if all the second order derivatives are greater than 0, the point is a global minimum and if all are smaller than 0 the point is a global maximum. A summary is shown in Figure 1.

Nf710 (talk) 12:53, 16 January 2018 (UTC) It is not necessarily a global maximum think about this on a 2D PES.

In this context of a potential energy surface, the first derivative corresponds to the Force and the second derivative corresponds to the force constant. A global minimum that shows the most stable and hence the lowest energy configuration will have the first derivative (in all 3N-6 dimensions) equal to 0 and the second derivative (in all 3N-6 dimensions) greater than 0.

A transition state (TS) is defined as the highest energy configuration on the lowest energy path between reactants and products. This can be thought of as a saddle point in 2D in which it is a minimum along one of the two dimensions, and a maximum along the other one. Similarly, in 3N-6 dimeansion, it is expected that one force constant (second derivative) is negative and all the other ones are positive. This can be checked by looking at the vibrations computed. Considering the link between the force constant $k$ and $ν$ , the frequency of molecular vibration, it becomes obvious how a negative force constant leads to a imaginary frequency which in Gaussian is displayed with a negative sign. In the equation below $μ$ is the reduced mass.

$ν = \frac{1}{2 π} \sqrt{\frac{k}{μ}}$

Using a similar reasoning, there should be no imaginary frequencies for structures optimised to a minimum. All the force constants are expected to be positive with a gradient greater than 0 in all dimensions for a global minimum.

Nf710 (talk) 12:53, 16 January 2018 (UTC) You can get the force constants from the eigenvalues of the Hessian Matrix (The matrix of second derivatives)

Finding the Reaction Pathway with IRC

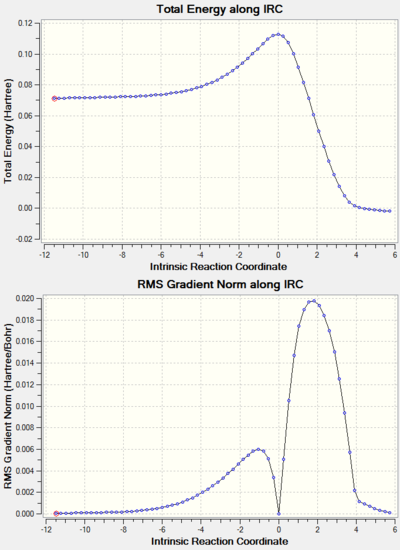
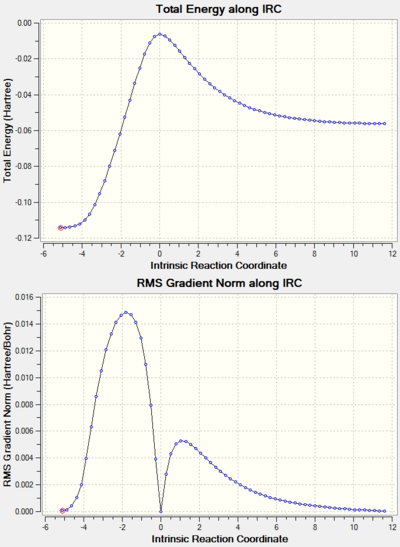
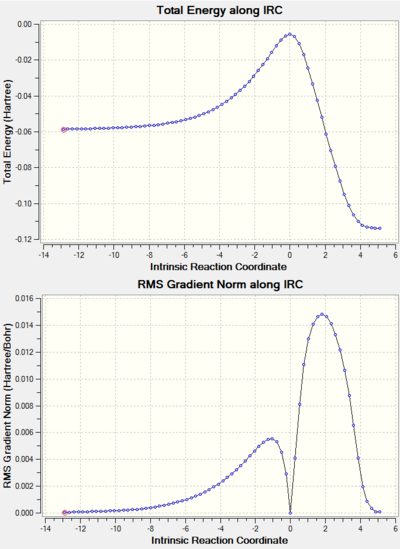
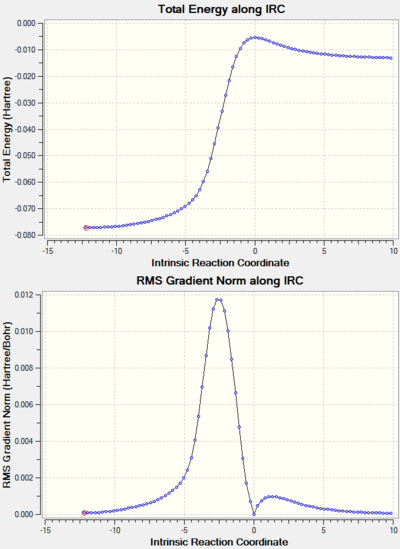
In order to find the link between reactants, TS and products, an IRC (intrinsic reaction coordinate) analysis can be done. This will find a series of constrained geometry optimisations which form the minimum energy reaction pathway. This is done by updating the Hessian matrix which stores all the second derivatives (i.e. force constants).

Moreover, an IRC analysis can confirm the transition state found if it finds a path to connect the reactants and products via the transition state.

Levels of Theory

Gaussian can operate using different methods or levels of theory that represent the set of approximations used to describe the chemical system. While higher levels of theory are more accurate, they come at a greater computational cost. For each level of theory, a basis set that consists of atomic orbitals (AOs) is needed to construct the wavefunction. The molecular orbitals (MOs) are then built as a linear combination of these atomic orbitals (LCAO). The ultimate purpose is to minimise the energy and this is done by 'guessing' an initial wavefunction and then updating the mixing coefficients of its components such that the lowest energy and hence the closest approximation to the real minimum is found.^[1]

Nf710 (talk) 12:58, 16 January 2018 (UTC) This is called the variational principle and it underpins all of quantum chemistry.

Three of the most common levels of theory and which were used in the calculations for this experiment are:

Semi-empirical

Semi-empirical methods use some experimental data throughout the calculation. This can dramatically speed up the calculations but might not be accurate enough. PM6 is one example of such a method. While the PM6 semi-empirical method uses an internal basis set, the density functional theory and ab initio methods do require a basis set specification.

Density Functional Theory (DFT)

DFT methods give results comparable to ab initio methods but are much faster as the energy is computed using electron density instead of wave functions. B3LYP (Becke, three-parameter, Lee-Yang-Parr) is a hybrid approximation that incorporates elements from the Hartree-Fock theory. One example of a basis set for this exchange correlation function is 6-31G(d).

Nf710 (talk) 12:58, 16 January 2018 (UTC) 6-31d can be used in a HF or DFT its is just one set of linear combinations of mathematical Gaussian functions that look like atomic orbitals. But good understanding of the hybrid nature of this functional

Hartree-Fock (HF)

This is an ab initio method in which the Coulombic electron-electron repulsion interactions are averaged and the wavefunction of the system is approximated by calculating the Slater determinant (for electrons). The variational method is then used to determine the energy and compute the molecular orbitals. STO-3G is a common minimal basis set that takes into account 3 weighting coefficients for the wavefunction calculation. This is a minimal set because it uses a minimum number of functions per atom to describe the occupied atomic orbitals. While this might not be accurate enough for quantitative results, it can give valuable qualitative information (e.g. chemical bonding).

Nf710 (talk) 12:58, 16 January 2018 (UTC)Good section. You have clearly gone beyond the script here and done further reading. Some equations of the Hamiltonian would back up the discussion of the basis sets and the quantum chemical methods

Methodology

The structures of the reactants and products were optimised to a minimum and checked not to have any imaginary frequencies. The product was used to find the transition state as follows:

The bonds formed in the reaction were 'broken' and the atoms involved were frozen at distances resembling those in the TS; the structure was optimised to a minimum.
With the atoms unfrozen, the resulting structure was optimised to a transition state (TS Berry) and checked to have exactly one imaginary frequency.
An IRC analysis was run on the TS structure obtained at the same level of theory.

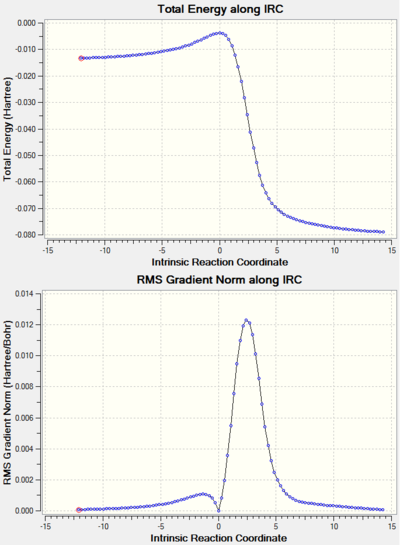
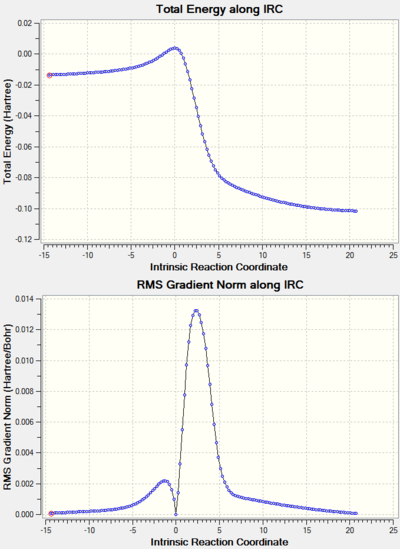
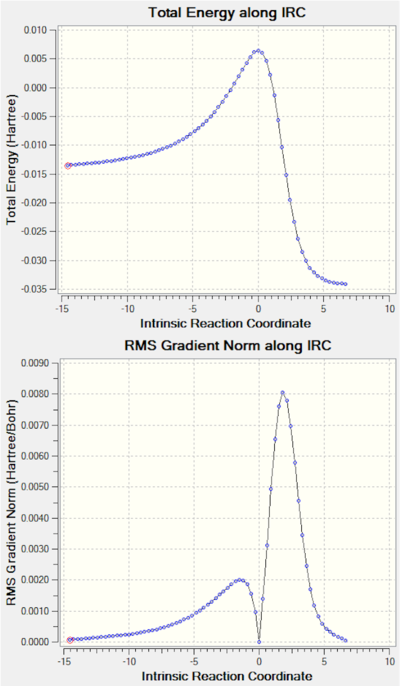
Note: the IRC results for all the reactions studied are shown at the end of the page in a separate section.

Exercise 1 - Reaction of Butadiene with Ethylene

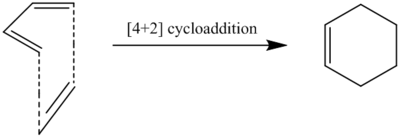
The reaction between butadiene and ethylene to yield cyclohexene is one of the simplest examples of cycloaddition reactions. The s-cis diene reacts with the dienophile in a [4+2] cycloaddition with an approach such as the one presented above. Overall, 2 sigma bonds are created and only one pi bond is left in the product.

Reactants and Products optimised at the PM6 level

Butadiene

Ethylene

Cyclohexadiene

An interesting thing to note is that the butadiene structure in the IRC has an imaginary frequency. This corresponds to the vibration that takes the s-cis conformation to the s-trans one, thus minimising the energy. Indeed, the s-trans conformation is lower in energy. However, it is the s-cis isomer that reacts in a DA reaction.

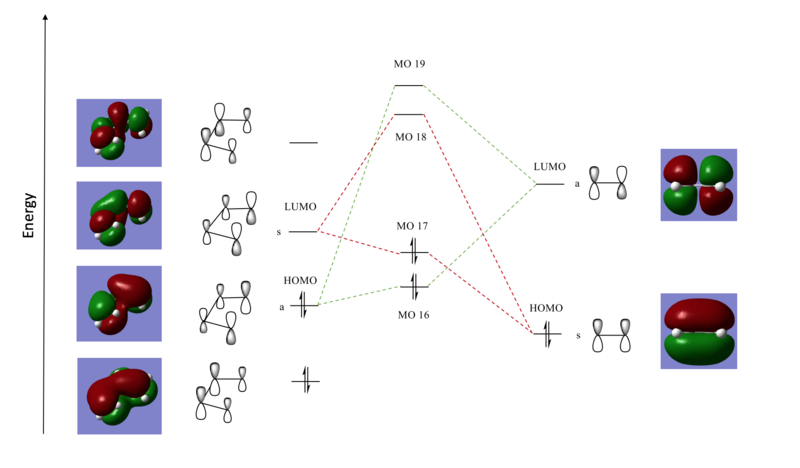
MO diagram

A qualitative MO diagram is shown and the interacting HOMOs and LUMOs were labelled s for symmetric and a for antisymmetric. This describes the MOs in terms of what phase the orbitals have upon inversion through the centre of symmetry of the molecule. The interacting MOs are those with the same symmetry and this is confirmed by the molecular orbitals of the transition state shown below. Butadiene and ethene each contribute with two MOs, yielding four MOs that have the same symmetry as the corresponding constituents. These are shown higher in energy than each of the contributing ones because the formation of a high energy transition state is shown. The relative energies of the MOs can be found from the IRC. For the product, the bonding MOs are expected to be stabilised more. Here, the HOMO of the electron rich diene (lower in energy) reacts with the LUMO of dienophile in a normal electron demand fashion.

(Fv611 (talk) A bit confused on why you have drawn the TS LUMO+1 and LUMO so high up in energy. Following the same reasoning on the bonding TS MOs being higher in energy than expected in the product MO combinations, the antibonding MOs will be lower in energy than expected. In this reaction, the ethene LUMO actually has the highest energy.)

The 4 MOs corresponding to the transition state are shown below.

MO16

MO17

MO18

MO19

Antisymmetric

Symmetric

Antisymmetric

The MOs have the same symmetry as the components they have resulted from and this can be described in terms of the overlap integral. The overlap integral is a measure of the extent at which the wave-functions describing the systems overlap. If A and B are two molecules reacting, the overlap integral over all space is given by:

$S_{a b} = \int Ψ_{A}^{*} Ψ_{B} d V$

Firstly, the closer the orbitals are, the better they overlap. Secondly, the symmetry of the combining MOs affects the resulting overlap. If they have different symmetries (symmetric - antisymmetric), the overlap integral is antisymmetric and technically vanishes. This corresponds to a low electron density between the nuclei. However, if both have the same symmetry, the overlap integral is symmetric and therefore non-zero. This corresponds to a stable configuration with a high electron density between nuclei which is what favours the formation of a new bond.

To sum up, the overlap integral is zero for interactions between orbitals that are either far away or with different symmetries and non-zero for symmetric-symmetric or antisymmetric-antisymmetric interactions. A reaction is allowed when the interacting orbitals have the same symmetry and are close enough in energy to interact.

C-C Bond lengths

Table 1: Diels-Alder C-C bond lengths
Bond	Bond length / Å
Bond	Reactants	Transition state	Products
C1-C4	1.335	1.380	1.501
C4-C6	1.468	1.411	1.338
C6-C8	1.335	1.380	1.501
C8-C14	3.414	2.115	1.540
C14-C11	1.327	1.382	1.541
C11-C1	3.414	2.115	1.540

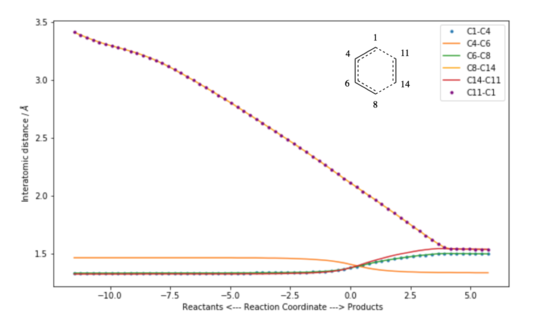
Figure 2 shows how the C-C bond lengths vary as the reaction proceeds. Considering the symmetry of the reactants and the product, some bonds are expected to be the same. The fact that they vary in the same way with respect to the reaction coordinate shows that the formation of the new bonds is synchronous (C8-C14 and C11-C1).

The bond lengths were also tabulated. All three double bonds increase as the transition state is approached and then turn into single bonds. The two single bonds neighbouring the double bond are slightly longer than the other ones. In comparison with the Van der Waals radius of the Carbon atom which is 1.7 Å, the length of the C-C bonds forming is smaller than the sum of two Van der Waals radii, but larger than what would be considered a bond. Moreover, an IRC analysis confirms the synchronous formation the bonds as seen in the GIF below.

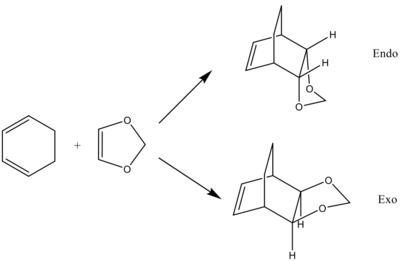
Exercise 2 - Reaction of Cyclohexadiene and 1,3-dioxole

In the first example, the dienophile (ethylene) was not substituted and only one approach was possible. With 1,3-dioxole however, the approach trajectory determines the stereochemistry of the product and two outcomes are possible: endo and exo.

Reactants and Products optimised at the B3LYP/6-31G(d) level

The same method was used to study this reaction. The reactants, products and transition state were first optimised at the PM6 level and then at the B3LYP/6-31G(d) level. Due to time constraints, the IRC was done at the PM6 level and the energies used to compare the reactants and the transition state in the MO diagram were these at the PM6 level.

Cyclohexadiene

1,3-Dioxole

endo Product

exo Product

MO Diagram

(Fv611 (talk) You have the python plot of the relative energies - why not draw your MO diagram accordingly? What makes the difference between this reaction and the previous one, and what makes this reaction an inverse electron demand is the fact that here the diene HOMO is the interacting orbital with the lowest energy, and the dienophile LUMO is the one with the highest energy.)

For the reaction of cyclohexadiene and 1,3-dioxole, the fragment orbitals look similar to the ones seen previously. However, the HOMO and the LUMO of the diene are higher in energy, leading to an inverse electron demand Diels-Alder. While the diagrams are expected to look similar for the endo/exo reactions, the endo TS MOs are expected to be slightly lower in energy. As seen before, the orbitals with same symmetry combine to give the MOs of the Transition State that have the same symmetry as their components. The endo and exo MOs are shown below (B3LYP level).

Endo

MO40

MO41

MO42

MO43

Exo

MO40

MO41

MO42

MO43

The relative energies of the MOs corresponding to reactants, transition state and products were plotted in Python for the two possible reactions and a comparison can be seen below. It should be noted that the structures for which the energy was calculated are the ones given by the IRC and this could be the reason why the spacing between energy levels (especially reactants) might not be very accurate. However, it gives a good idea of where the levels are.

Nf710 (talk) 13:03, 16 January 2018 (UTC) This is excellent and it gives you a clear idea of where the MOs lie relative to each other in the reactants and there you can see which MOs are interacting with each other. Well done.

Comparison of the Endo/Exo Products

The reaction barriers (or activation energy) and the reaction energies were calculated for the two reactions at the B3LYP/6-31G(d) level and a summary is shown in Table 2.

Table 2: Diels-Alder associated energies
	Reaction barrier		Reaction energy
	Hartrees/particle	kJ/mol	Hartrees/particle	kJ/mol
Endo	0.06036	158.46723	-0.02618	-68.74606
Exo	0.06334	166.30697	-0.02481	-65.15175

Both reactions are thermally favoured (negative reaction energies) and have relatively low energy barriers. The endo Diels-Alder has a lower activation energy. This means the TS will form faster and the reaction is kinetically favoured. The results can be explained using the Frontier Molecular Orbital Theory (FMO). The ‘’primary orbital interactions’’ determine whether the product can form and require the constructive overlap of the orbitals corresponding to the atoms between which the new bonds are formed. By looking at the ‘’secondary orbital interactions’’ between the LUMO of cyclohexadiene and the HOMO of 1,3-dioxole (computed structure can be seen in the MO digram), it can be understood why the endo transition state is more stable. The orbitals of the oxygen atoms can interact with two carbon orbitals between which the double bond will form to lower the energy. However, this interaction does not happen in the exo TS. This is shown in Figure 3 and is in agreement with the ‘’’endo rule’’’ which states that the endo product is favoured in irreversible Diels-Alder processes.

Although it is often found that the exo product is lower in energy, the reaction energy is more negative for the endo reaction in this situation. This can be explained by considering the steric clash between the CH2 group of the heterocycle with the bridging C atoms which avoided in the endo product.

Nf710 (talk) 13:05, 16 January 2018 (UTC) Your energies are correct and you have come to the correct conclusions well done. You could have added a diagram to aid your discussion on the steric clashes. excellent use of the IRC MOS to determine the relative ordering of the MOs in the reactants.

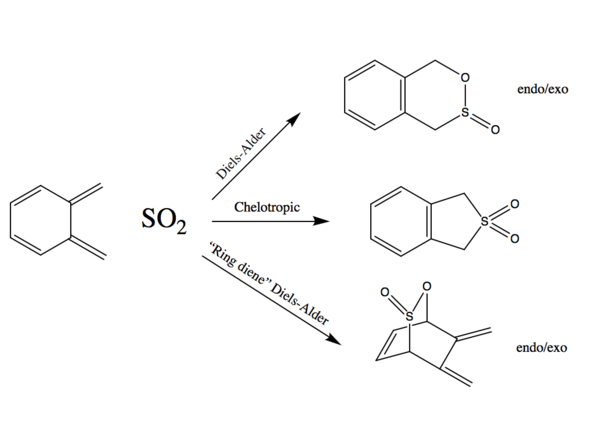
Exercise 3 - Diels-Alder vs Cheletropic

When o-xylyline and SO2 are reacted together, a few outcomes are possible. The reaction can be either chelotropic or Diels-Alder with two possible cis-butadiene fragments that can each react in an endo/exo manner.

Energy Calculations

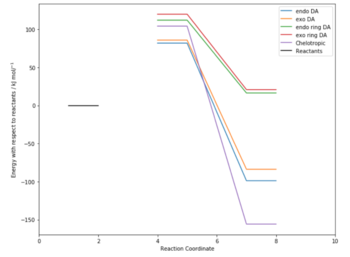
The five possible outcomes were optimised at the PM6 level and a summary of the energies computed is shown in Figure 4 with the 0 energy level set as the energy of the reactants at infinite separation. It quickly becomes obvious that the most probable outcomes are the chelotropic and the endo/exo Diels-Alder in which the conjugated double bonds outside the ring are reacting. Although there is an energy difference between the endo/exo transition states, they are relatively close in energy. Indeed, as it can be seen in the vibration showing the isomerisation of the transition state, the structure does not change very much.

When SO₂ reacts with the conjugated double bonds that are outside the ring, the transition state is highly stabilised by the the formation of the aromatic benzene ring with (4n+2) $π$ electrons. All three reactions are thermodynamically favoured, giving an aromatic product.

If SO₂ reacts with the butadiene fragment that is part of the 6-membered ring, the large stabilisation given by the formation of the benzene ring can no longer occur. Indeed, the energy barrier is much larger in this case. Moreover, the products of this Diels-Alder reaction are much higher in energy (higher energy than products) as the aromatic stabilisation is lost and the compounds are more sterically hindered. These factors make the reactions at this site very unlikely as they are both thermodynamically and kinetically unfavourable. A summary of the data is shown in Table 3.

(Good intro. Probably the first person to realise endo and exo can isomerise. Did you look at the energies for this to determine whether, at reaction conditions, endo will invariably isomerise to exo? This TS can be added to the reaction profile. Additionally, there are TSs to link the cheletropic product to the DA products Tam10 (talk) 16:33, 9 January 2018 (UTC))

Table 3: Energies associated with the possible reactions between o-xylylene and SO₂.
	Energy barrier		Reaction energy
	Hartrees/particle	kJ/mol	Hartrees/particle	kJ/mol
Endo DA	0.03120	81.91556	-0.03767	-98.88941
Exo DA	0.03272	85.90107	-0.03192	-83.79280
Chelotropic	0.03970	104.23493	-0.05937	-155.86799
Endo DA (ring)	0.04271	112.13768	0.00625	16.41199
Exo DA (ring)	0.04570	119.97217	0.00794	20.85959

The results of the IRC are shown below for the three thermodynamically favoured reactions. It is interesting to note how the benzene ring forms quite early in the process.

Endo DA	Exo DA	Chelotropic

(Why would the cheletropic product be the lowest in energy? Tam10 (talk) 16:33, 9 January 2018 (UTC))

Relevant Files

Diels-Alder endo TS - File:Dt2315 ex3 ENDO DA TS PM6.LOG
Diels-Alder endo product - File:Dt2315 ENDOPRODUCTS MINIMUM PM6.LOG
Diels-Alder exo TS - File:Dt2315 ex3 exoDA TS PM6.LOG
Diels-Alder exo product - File:Dt2315 EXOPRODUCT OPT PM6.LOG
Chelotropic TS - File:Dt2315 CHELOTROPIC TS PM6.LOG
Chelotropic product - File:Dt2315 chelotropic MINIMUM PM6.LOG
'Ring' Diels-Alder endo TS - File:Dt2315 RING ENDO TS PM6.LOG
'Ring' Diels-Alder endo product - File:Dt2315 RING ENDO PROD MIN PM6.LOG
'Ring' Diels-Alder exo TS - File:Dt2315 RING EXO TS PM6.LOG
'Ring' Diels-Alder exo product - File:Dt2315 RING EXO PROD MIN PM6.LOG

Electrocyclic Reactions

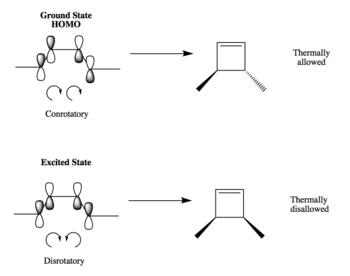
Electrocylic reactions are pericyclic processes in which a a sigma bond forms across the ends of a conjugated polyene. The cyclisation of 1,4-dimethyl-1,3-butadiene was studied using the same methodology as the one described at the beginning at the Hartree-Fock/STO-3G level.

As predicted by the Woodward Hoffmann analysis, all thermal electrocylic reactions with $(4 n) π$ electrons are conrotatory and the product was chosen to be the one with the methyl groups on opposite sides of the cyclobutane ring. This can be seen in Figure 5 how the p orbitals at the end of the double bonds need to both rotate clockwise to form a new sigma bond. The disrotatory cyclisation that would give the methyl groups on the same side is thermally disallowed. However, the reaction is possible under photochemical conditions by exciting the electrons to a higher energy state which would require the p orbitals to rotate one clockwise and one counterclockwise in order to form a new sigma bond such as the one shown.

Figure 6. The thermally allowed electrocylic reaction

CASSCF (Complete Active Space Multiconfiguration SCF) provides a way of looking at excited electrons and was used to find the excited state that would lead to the disrotatory reaction being possible. The analysis computes a subset of states known as the active space^[2]. The settings used are shown below.

%oldchk=H:\Y3\TS\Extension\initial_HF.chk       
%chk=H:\Y3\TS\Extension\opt_CAS.chk
%nproc=4
%mem=2000MB
#p opt freq guess=read geom=allcheck casscf(4,4,nroot=2)  //4 electrons, 4 molecular orbitals and the state of interest is 2

(Just for the sake of pedantry, different types of orbitals may be used in a CASSCF calculations. It's often easier to work with localised orbitals Tam10 (talk) 16:48, 9 January 2018 (UTC))

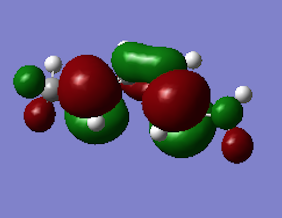
Figure 7. The excited state of 1,4-dimethyl-1,3-butadiene found using CASSCF

By looking at the four highest energy electrons and four corresponding orbitals, the spin configurations for the ground state and the excited state were found. The two main contribution for each state are shown in Figure 8. Interestingly, the electrons are excited to the second higher energy state and this was drawn in Figure 5 showing the disrotatory cyclisation. The excited state MO does indeed confirm the structure.

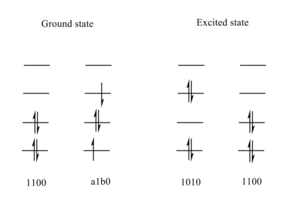
Continuing the analysis, it was tried to find the conical intersection of the ground state and the excited state with opt=conical. This approach tries to bring the states closer in energy to each other, until they become degenerate. This was tried starting with the products of the excited state. However, it proved to be particularly challenging as the PES of the thermally disallowed reaction is probably much higher in energy than the PES of the thermally allowed reaction. A good indicator of this is the very large energy difference between the ground state and the excited state in which the reactant would need to be for a disrotatory process to occur (almost 800 kJ/mol).

(A good effort, with some cool results. CASSCF is a very challenging method Tam10 (talk) 16:48, 9 January 2018 (UTC))

(+12%)

Conclusion

The results given by Gaussian in the study of cycloadditions and electrocylic reactions are in agreement with existing theory such as the endo rule or the Woodward-Hoffmann rules. While some knowledge of the structure of the products was required, the computational methods used allowed the study of numerous outcomes that would have been much more difficult and time consuming to investigate experimentally. Moreover, this approach can help better understanding the reaction mechanisms and pathways. Using more accurate levels of theory such as Hartree-Fock also allowed the study of a thermally disallowed electrocylic reaction.

References

1. Szabo, A. & Ostlund, Neil S, "Modern quantum chemistry: introduction to advanced electronic structure theory", Mineola, N.Y; London, Dovere, 1996.

2. McDouall, Joseph J. W, "Computational Quantum Chemistry: Molecular Structure and Properties in Silico" RSC theoretical and computational chemistry series 5", Royal Society Of Chemistry, 2013.

3. J. Clayden, N. Greeves, S. Warren and P. Wothers, “Organic Chemistry”, Oxford University Press, Oxford, 2001.