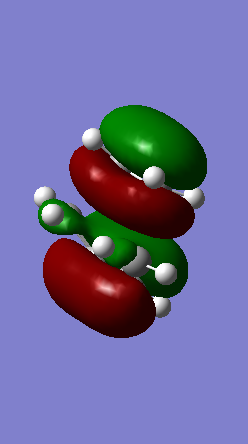Rep:Mod:dp2615

TRANSITION STRUCTURES AND REACTIVITY COMPUTATIONAL LAB WIKI REPORT

Introduction

Linking potential energy, transition state and reaction path

Chemical reactions can be explored by examination of relative energies of reactants, transition states and products. The point of focus during a chemical reaction is the transition state as it offers information on the energy barrier of the reaction which can lead to other crucial conclusions about reaction dynamics.

The potential energy of a chemical reaction is a function of the internuclear distances between all the atoms. This function is hard to calculate and can be simplified to fewer and specific internuclear distances as a simplification. On a potential energy surface the transition state is considered as the saddle point. All reactive pathways are calculated to go through this crossing, sometimes called "mountain pass", i.e. the transition state.

Nf710 (talk) 22:01, 30 November 2017 (UTC) this is not coreect, there can be more than one TS, different reaction pathways etc. Also the PES is in 3N-6 degrees of freedom for dimensions not inter nuclear distance.

Mathematically speaking, the height of this saddle point corresponds to the maximum energy point on the minimum energy reaction path. The gradient and curvature of a saddle point are zero, meaning both the first and second derivatives are zero. It can be also identified as the lowest local maximum of the energy plot. ^[1]

Nf710 (talk) 22:04, 30 November 2017 (UTC) At a TS the graient is zero. the curvature is positive in 3N-6 degrees of freedom. And then negative in 1 which is the reaction coordinate.

The minimum energy reaction path goes straight up through the transition state and then falls down to the products. In this non-ideal reality many reactions go through the region around the transition state and therefore do not cross directly on the saddle point. This can be rationalised by assuming that more kinetic energy than precisely the activation energy has been given to the molecules resulting in a slightly higher energy reaction path.

It is possible to confirm from a frequency calculation that a structure is at the transition state, and so at the saddle point, because the first frequency will result as negative while all the other ones will be positive. This is because at a transition state there is one vibration toward the products which lowers the energy rather than increasing it which gives a negative frequency.

Nf710 (talk) 22:04, 30 November 2017 (UTC) This is correct. You coudl have gone into abit of detail about the quantum chemical methods here.

Exercise 1

Comparing bond lengths of a Diels-Alder reaction

A Diels-Alder reaction is a [4+2]-cycloaddition which proceeds via a cyclic transition state to create two new sigma bonds:

Figure 1. Diels-Alder reaction between butadiene and ethene.

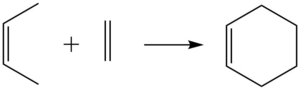
In this concerted pericyclic reaction, the formation of the two sigma bonds is synchronous as illustrated below where the vibration of the transition state corresponding to the reaction pathway is shown:

Figure 2. Diels-Alder transition state vibration.

Literature^[2] reports by means of X-ray and neutron diffraction the following typical bond lengths (Å):

C-C bond lengths

Type of bond	Bond length (Å)
C sp3- C sp3	1.51
C sp3- C sp2	1.50
C sp2- C sp2	1.46

The Van der Waals radius of C atom is reported^[3] as : 1.70

The C-C bond lengths of reactants(Å), transition state and product are listed below to show their progression throughout the reaction:

C-C bond lengths of reactants

Molecule	Bond length (Å)
Butadiene	1.34 (double bonds); 1.47 (single bond)
Ethene	1.36

C-C bond lengths at transition state

Molecule	Bond length (Å)
Butadiene	1.36 (end bonds); 1.44 (central bond)
Ethene	1.36
New sigma bonds	2.11

C-C bond lengths of product

New sigma bond	Bond length (Å)
Single bonds	1.54
Double bond	1.34

The most significant change of bond length between the reactants and transition state is that of the butadiene molecule. The bond compresses from 1.47 Å to 1.44 Å, thus resulting in a change of the angle between the carbons from 125° to 120° as the molecule adapts its conformation to align the orbitals for the interaction with ethene at the transition state which will lead to the formation of cyclohexene. The end bonds of butadiene present no change in length. Ethene shows no change of conformation between reactant and transition state.

The product shows an elongation of single bonds to 1.54 Å, but the same double bond length as the original butadiene molecule.

It is clear from all the bond lengths observed in these molecules that a covalent C-C bond is not the sum of the Van der Waals radii of the two carbon atoms (2.4 Å) (Fv611 (talk) 3.4), but instead a length produced from a strong interaction which results in a closer approach of the two atoms to each other.

(Fv611 (talk) You are missing the comparison between the length of the C-C bonds being formed and the typical length of sp3-sp3 bonds.)

Molecular Orbital Theory

(Fv611 (talk) Unfortunately you misunderstood what you were asked to do, which was a comparison of the energies of the HOMO/LUMO pairs in both reactants and the energies of their linear combinations at the TS, not at the product. This was clear in the exercise question. Another thing to note is that the symmetry requirements are not specific to Diels-Alder reactions. I also think that the orbitals you showed as pictures are from the TS, not like the product like you state they are.)

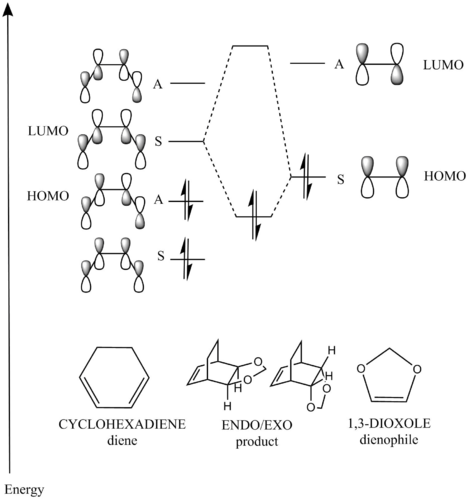
Molecular Orbital Theory allows us to represent chemical bonds by combining the orbitals of the reactants to make new complex molecular orbitals (MOs). Only fragment orbitals of the same symmetry can interact to form a bonding-antibonding pair. The strong interaction that is usually present between a HOMO (Highest Occupied MO) and LUMO (Lowest Unoccupied MO) pair results in stabilised MOs. Both the atomic orbitals must have the same symmetry label in order to form new orbitals. In the case of a Diels-Alder reaction, this pair of orbitals must either be symmetric or anti-symmetric for the reaction to be allowed. Any other combination of symmetry would result in a forbidden reaction as the overall stabilisation is not more than that of the starting orbitals.

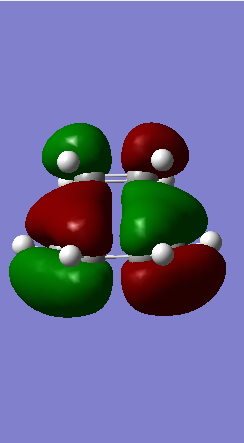
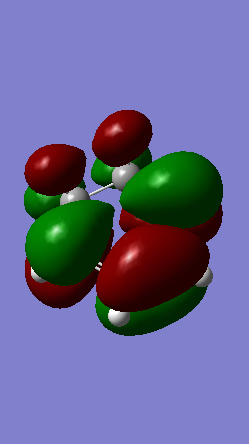
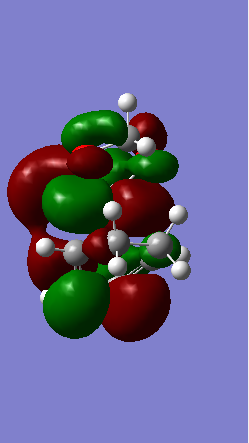
Shown below in figure 3 is the MO diagram of this Diels-Alder reaction with the relevant interaction that leads to bond formation:

Figure 3. MO diagram of this Diels-Alder reaction.

MOs can be defined as many electron wavefunctions governed by their variant of the Schrödinger equation. This equation has a component S_ab called the orbital overlap integral which measures the extent to which the two atomic orbitals overlap. This integral is zero for interactions between orbitals with different symmetry, and not zero for a symmetric—anti-symmetric interaction. (Fv611 (talk) This sentence contradicts itself. Proofreading would have avoided this!) This agrees with the symmetry requirement of MO theory.

The relevant HOMO-LUMO pair was determined by examination of the MOs involved in this reaction shown below. It is clear that the HOMO and LUMO of the product are symmetric MOs thus the HOMO-LUMO pair that combines to form these MOs must have the same symmetry, and therefore corresponds to the symmetric, not the anti-symmetric, interaction.

Figure 4. HOMO of ethene.	Figure 5. LUMO of butadiene.	Figure 6. Second highest occupied MO of product.	Figure 7. HOMO of product.	Figure 8. LUMO of product.	Figure 9. Second lowest unoccupied MO of product.

LOG FILES

Here are listed the log files of all the relevant calculations carried out to complete this exercise:

LOG FILES

Name of log file	description
File:ETHYLENE MOS dp2615.LOG	optimisation of ethene molecule
File:BUTADIENE MOS dp2615.LOG	optimisation of butadiene molecule
File:TS WITH MOS FOR JMOL dp2615.LOG	transition state calculation at PM6 level
File:TS FREQ dp2615.LOG	transition state frequency check
File:IRC dp2615.LOG	IRC calculation at PM6 level
File:PRODUCT OPT 3 dp2615.LOG	final product optimisation

Exercise 2

Molecular Orbitals in a Diels-Alder reaction

Figure 10. Diels-ALder reaction between cyclohexadiene and 1,3-dioxole.

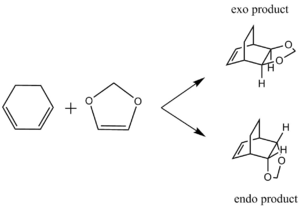
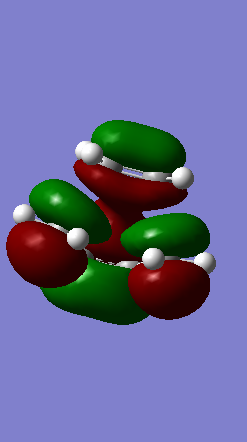
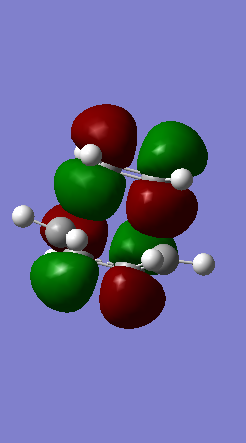
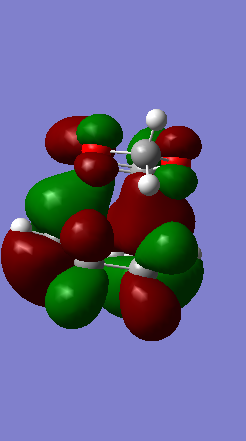
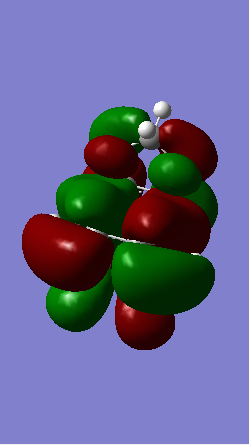
A Diels-Alder reaction between an electron deficient diene and an electron rich dienophile is an inverse electron demand pericyclic reaction. In this case, the diene is not completely electron deficient as there is a small extent of positive inductive effect from the cyclic carbon group attached to the diene. However, the dienophile is under strong effect of two ether groups which are highly electron donating, therefore pushing this reaction towards an inverse electron demand interaction rather than a normal electron demand reaction. This is proven by the observed symmetry of the MOs of the two reagents at the transition state where both the HOMO and LUMO appear to be symmetric thus supporting the inverse electron demand requirements:

Figure 11. MO diagram of this Diels-Alder reaction.

Below are shown the relevant MOs of this reaction to prove that the interaction is between a symmetric HOMO-LUMO pair:

(Fv611 (talk) As before, this isn't a Transition State MO diagram. The way you have drawn it the LUMO of the TS would be antisymmetric, however you know that's not the case because you have shown the correct LUMO in your table. Should have correlated the diagram and your computed MOs.

Figure 12. HOMO of 1,3-dioxole.	Figure 13. LUMO of cyclohexadiene.	Figure 14.Second highest occupied MO of exo product.	Figure 15. HOMO of exo product.	Figure 16. LUMO of exo product.	Figure 17. Second lowest unoccupied MO of exo product.

Figure 18. HOMO of 1,3-dioxole.	Figure 19. LUMO of cyclohexadiene.	Figure 20.Second highest occupied MO of endo product.	Figure 21. HOMO of endo product.	Figure 22. LUMO of endo product.	Figure 23. Second lowest unoccupied MO of endo product.

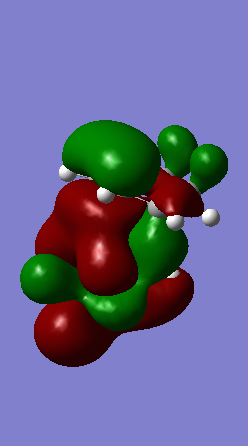
Also relevant is the fact that in figure 21 a secondary orbital overlap can be observed between the oxygen p orbital and π C-C bond orbital which stabilises the molecule thus lowering its energy and making the endo product the thermodynamically favourable one.

Thermochemistry

Below is a table showing the sum of the electronic and thermal free energies of both the endo and exo reaction pathways calculated using B3YLP calculations:

Reactants

Molecule	Gibbs Free Energies (hartrees)	Gibbs Free Energies (kJ/mol)
cyclohexadiene	-233.321033	-612584.418806
1,3-dioxole	-267.068132	-701187.43398
sum of reactants	-500.389165	-1313771.85279

ENDO adduct

Molecule	Gibbs Free Energies (hartrees)	Gibbs Free Energies (kJ/mol)
transition state	-500.332151	-1313622.16252
product	-500.418691	-1313849.3733

EXO adduct

Molecule	Gibbs Free Energies (hartrees)	Gibbs Free Energies (kJ/mol)
transition state	-500.329165	-1313614.32277
product	-500.417322	-1313845.77899

Activation energies

	endo adduct	exo adduct
in hartrees	0.057014	0.06
in kJ/mol	149.6902684	157.53

Is it deduced from these activation energies that the thermodynamically favourable reaction path is the one that leads to the exo product, whereas the kinetically favourable path is the one leading to the endo product. The difference in energies between the to energy barriers is 7.84 kJ/mol.

The thermodynamically favourbale product is the endo product which would require a higher activation energy for its transition state, but in this case carries a lower (more negative) kinetic energy barrier. However, it has only a 3.59 kJ/mol energetic difference with the exo product, so could be considered a non-significant diversion form typical Diels-Alder behaviour.

Nf710 (talk) 22:11, 30 November 2017 (UTC) You have said that the themro product is both the exo and the endo. but you have deduced the kenetic product correctly. You should have also tabulated your reaction energies

This goes to show that the endo product is favoured thermodynamically as well as kinetically. The endo product of this Diels-Alder reaction is usually found to be the kinetic product, thus partly agreeing with these findings and so the predicted pathways partly validates these results. The diversion of selectivity can be rationalised by considering the secondary orbital overlap of the p orbitals of the oxygen atoms with the π orbitals of the diene which stabilises the transition state of the endo adduct, in this case enough to pull it down to a kinetic barrier as for the case of cyclopentadiene and maleic anhydride.

Nf710 (talk) 22:11, 30 November 2017 (UTC) OK I will let you off but this section is not very clear

LOG FILES

Here are listed the log files of all the relevant calculations carried out to complete this exercise:

LOG FILES

Name of log file	description
File:DIOXOLE OPT B3YLP dp2615.LOG	optimisation of 1,3-dioxole
File:CYCLOHEXADIENE OPT B3YLP dp2615.LOG	optimisation of cyclohexadiene
File:ENDO OPT PM6 2 dp2615.LOG	optimisation of endo structure pre-transition state
File:ENDO TS PM6 dp2615.LOG	transition state calculation of the endo structure at PM6 level
File:ENDO TS B3LYP dp2615.LOG	transition state calculation of the endo structure at B3YLP level
File:ENDO PM6 IRC OF PM6 dp2615.LOG	IRC calculation on the transition state optimised at PM6 level
File:ENDO PRODUCT B3YLP OPT dp2615.LOG	optimisation of endo product
File:EXO OPT PM6 dp2615.LOG	optimisation of exostructure pre-transition state
File:EXO TRANSITION STATE PM6 dp2615.LOG	transition state calculation of the exo structure at PM6 level
File:EXO TRANSITION STATE B3YLP dp2615.LOG	transition state calculation of the endo structure at B3YLP level
File:EXO FROM TS PM6 IRC dp2615.LOG	IRC calculation on the transition state optimised at PM6 level
File:EXO PRODUCT OPT B3YLP dp2615.LOG	optimisation of exo product

Nf710 (talk) 22:11, 30 November 2017 (UTC) You could have shown the SOO with a nice diagram or JMOL

Exercise 3

Background chemistry

A Diels-Alder reaction is a [4+2]-cycloaddition, whereas a cheletropic reaction is a pericyclic reaction considered as a subclass of cycloadditions in which a reorganisation of σ and π bonds occurs at the same atom in the cyclic array of atoms at the transition state.

In many cases, the cheletropic five-membered ring product is the thermodynamic product while the Diels-Alder adducts are the kinetically favoured ones. An example is the addition of SO₂ to 1,2-dimethylidenecyclohexane. In the case presented here, however, the conjugation of the hexane ring plays an important part in the lowering of the energy of both the Diels-Alder adducts by aromatisation in comparison to the cheletropic product.

(Citations would be useful here. Aromatisation affects the cheletropic reaction too, but you have the wrong product Tam10 (talk) 14:59, 27 November 2017 (UTC))

Figure 24. Diels-Alder and Cheletropic o-xylylene-SO₂ cycloaddition.

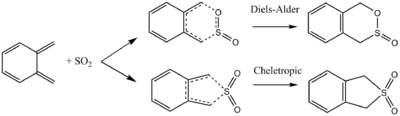
Thermochemistry of Diels-Alder and Cheletropic reactions

Below is a table showing the sum of the electronic and thermal free energies of both the endo, exo and cheletropic reaction pathways calculated using PM6 optimisations:

Reactants

Molecule	Gibbs Free Energies (hartrees)	Gibbs Free Energies (kJ/mol)
o-xylylene	0.178764	469.344918
SO2	-0.119268	-313.1381579
sum of reactants	0.059496	156.20676

Diels-Alder ENDO adduct

Molecule	Gibbs Free Energies (hartrees)	Gibbs Free Energies (kJ/mol)
transition state	0.090558	237.760047
product	0.021711	57.0022348

Diels-Alder EXO adduct

Molecule	Gibbs Free Energies (hartrees)	Gibbs Free Energies (kJ/mol)
transition state	0.092078	241.750807
product	0.021455	56.3301068

Cheletropic adduct

Molecule	Gibbs Free Energies (hartrees)	Gibbs Free Energies (kJ/mol)
transition state	0.099054	260.066297
product	0.063328	166.267677

(Your cheletropic product is too high in energy. You are missing 2 hydrogens in the structure Tam10 (talk) 14:59, 27 November 2017 (UTC))

Activation energies

	endo adduct	exo adduct	chelatropic adduct
in hartrees	0.031062	0.032582	0.039558
in kJ/mol	81.5532872	85.5440475	103.859537

Reaction energies

	endo adduct	exo adduct	chelatropic adduct
in hartrees	-0.037785	-0.038041	0.003832
in kJ/mol	-99.20452506	99.87665311	10.0609168

Is it deduced from these energies that the thermodynamically favourable reaction path is the one that leads to the Diels-Alder exo product as it has a larger reaction energy requirement, whereas the kinetically favourable path is the one leading to the endo product with a smaller energy barrier. The endo product also shows a higher product energy proving it is the kinetic product.

The cheletropic product has a higher energy and a higher transition state energy than both the Diels-Alder adducts. It has negative reaction energy, meaning it is an endothermic reaction and requires an input of energy for its completion unlike the exothermic Diels-Alder reactions.

Figure 25. Reaction profile of Diels-Alder and Cheletropic reactions.

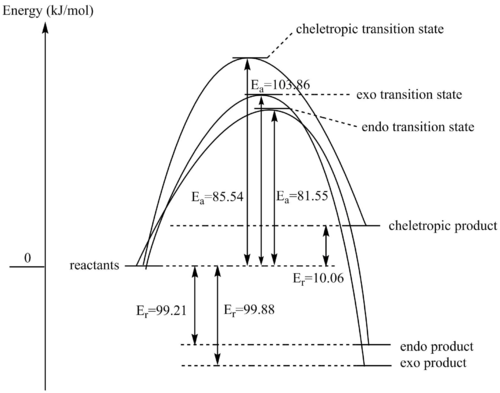
(Don't use curves for reaction profiles Tam10 (talk) 14:59, 27 November 2017 (UTC))

In the reaction profile above, E_a represent the activation energies and E_r represent the reaction energies.

This reaction profile shows the relative energies of the Diels-Alder and cheletropic cycloadditions. The reactant energy level has been set to 0 as the reactant molecules are being considered at infinite separation, and the energy barriers for the transition states as well as the energies of the products are reported to demonstrate thermodynamic and kinetic favourability of these reactions.

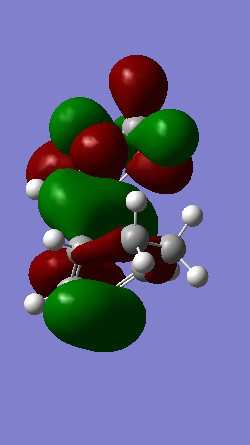
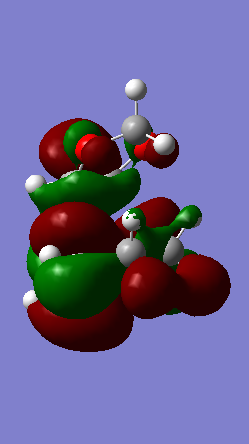
Looking at the IRCs of the Diels-Alder reactions, it can be observed that the double bonds of the six-membered ring of o-xylylene delocalise across the entire ring during the course of the reaction and then go to the make the final aromatic product. This aromatisation is what stabilises the reaction thus lowering its overall energy barrier.

Figure 26. IRC path of exo product.

Figure 27. IRC path of endo product.

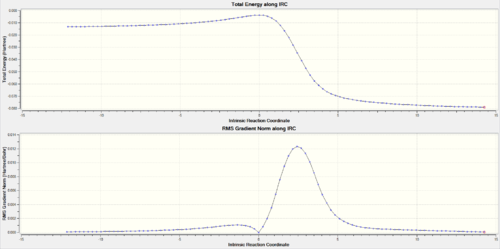
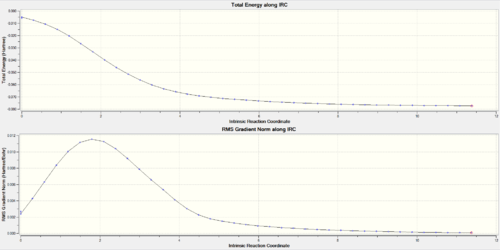
(The gradient for the initial geometry is wrong for the endo IRC. This can mean you've used a frozen geometry, or an inconsistent method/basis set Tam10 (talk) 14:59, 27 November 2017 (UTC))

Figure 28. IRC path of cheletropic product.

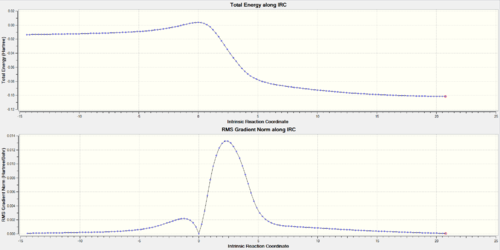
LOG FILES

Here are listed the log files of all the relevant calculations carried out to complete this exercise:

LOG FILES

Name of log file	description
File:OPT OF SO2 dp2615.LOG	optimisation of SO2
File:STARTING MATERIAL OPT dp2615.LOG	optimisation of o-xylylene
File:OPTIMISATION OF PRODUCT dp2615.LOG	optimisation of product for pre-transition state analysis
File:OPTIMISATION PRE-TS 2 dp2615.LOG	optimisation of exo structure pre-transition state
File:EXO TS PM6 6 dp2615.LOG	transition state calculation of the endo structure at PM6 level
File:EXO FROM TS PM6 6 IRC dp2615.LOG	IRC calculation on the transition state optimised at PM6 level
File:EXO PRODUCT OPT dp2615.LOG	optimisation of exo product
File:ENDO OPTIMISATION PRE TS dp2615.LOG	optimisation of endo structure pre-transition state
File:ENDO TRANS STATE dp2615.LOG	transition state calculation of the exo structure at PM6 level
File:ENDO FINAL IRC dp2615.LOG	IRC calculation on the transition state optimised at PM6 level
File:ENDO OPT PRODUCT dp2615.LOG	optimisation of endo product
File:EXO OPTIMISATION PRE-TS dp2615.LOG	optimisation of cheletropic structure pre-transition state
File:EXO TRANSITION STATE dp2615.LOG	transition state calculation of the cheletropic structure at PM6 level
File:EXO IRC dp2615.LOG	IRC calculation on the transition state optimised at PM6 level
File:OPTIMISATION PRODUCT dp2615.LOG	optimisation of cheletropic product

Thermochemistry of the secondary Diels-Alder reactions

o-xylylene contains a second cis-butadiene fragment within the hexadiene ring which can undergo Diels-Alder reactions. Below is a table showing the sum of the electronic and thermal free energies of both the endo and exo reaction pathways calculated using PM6 optimisations:

Reactants

Molecule	Gibbs Free Energies (hartrees)	Gibbs Free Energies (kJ/mol)
o-xylylene	0.178764	469.344918
SO2	-0.119268	-313.1381579
sum of reactants	0.059496	156.20676

Diels-Alder ENDO adduct

Molecule	Gibbs Free Energies (hartrees)	Gibbs Free Energies (kJ/mol)
transition state	0.102070	267.984805
product	0.065610	172.259068

Diels-Alder EXO adduct

Molecule	Gibbs Free Energies (hartrees)	Gibbs Free Energies (kJ/mol)
transition state	0.105054	275.819298
product	0.067304	176.706665

Activation energies

	endo adduct	exo adduct
in hartrees	0.042574	0.045558
in kJ/mol	111.778046	119.612538

Reaction energies

	endo adduct	exo adduct
in hartrees	0.006114	0.007808
in kJ/mol	16.0523082	20.4999056

From these energies it can be deduced that the endo adduct is both the thermodynamic and kinetic product as it holds a lower reaction energy barrier but also a lower product energy. However, this reaction is extremely unfavourbale when comparing these energies to the ones of the Diels-Alder reactions on the external diene. Is it thermodynamically and kinetically unfavourbale because the energy barrier is extremely high and the final products' energies are higher than the reactants making this an endothermic process.

Figure 29. IRC path of exo product.

Figure 30. IRC path of endo product.

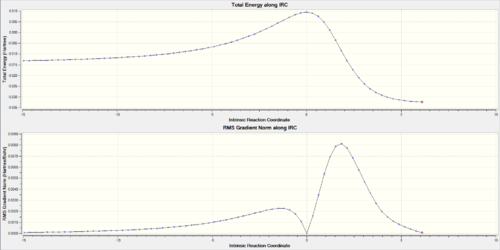
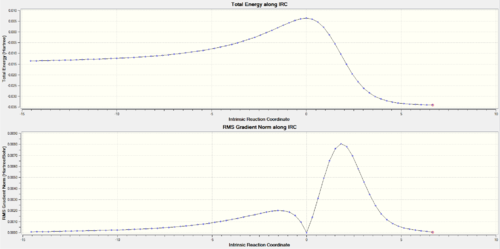
LOG FILES

Here are listed the log files of all the relevant calculations carried out to complete this exercise:

LOG FILES

Name of log file	description
File:EXO OPTIMISATION EXTENSION dp2615.LOG	optimisation of exo structure pre-transition state
File:EXO TS EXTENSION dp2615.LOG	transition state calculation of the endo structure at PM6 level
File:EXO IRC EXTENSION dp2615.LOG	IRC calculation on the transition state optimised at PM6 level
File:EXO EXTENSION PRODUCT OPT dp2615.LOG	optimisation of exo product
File:ENDO OPT EXTENSION dp2615.LOG	optimisation of endo structure pre-transition state
File:ENDO TS EXTENSION dp2615.LOG	transition state calculation of the exo structure at PM6 level
File:ENDO IRC EXTENSION dp2615.LOG	IRC calculation on the transition state optimised at PM6 level
File:ENDO EXTENSION PRODUCT OPT dp2615.LOG	optimisation of endo product

References

[1] Pascanu R., Dauphin Y., Ganguli S., Bengio Y., "On the saddle point problem for non-convex optimisation", Cornwell Univeristy, 2014.

[2] Allen F., Kennard O., Watson G., Brammer L., Orpen A., Taylor R., "Tables of Bond Lengths determined by X-Ray and Neutron Diffraction. Part I.Bond Lengths in Organic Compounds", J. CHEM. SOC. PERKIN TRANS. II, 1987.

[3] Bondi A., "van der Waals Volumes and Radii", The Journal of P̪hysical Chemistry VOLUME 68, NUMBER 3 MARCH 16, 1964.