Rep:Mod:don'tpanic

Introduction

This module involves computational studies into the bonding and structure of inorganic compounds, complexes and ligands. The compounds looked at in the first part will be BCl₃ BH₃, Cis and Trans Mo(CO)₄L₂.

The mini-project is concerned with molecular orbital analysis of ligands based on cyclopentadiene with added electron donating groups or electron withdrawing groups. Orbitals of Fe(C₅H₅)(CO)₂Cl were computed to show the interaction of the MO's with metal d-orbitals.

Module 2

BCl₃ Optimisation and Frequency Calculation

This part of the module is concerned with using computational MO methods rather than the simpler molecular mechanics methods to predict properties of D_3h symmetric BCl₃

The calculation method which determines the approximations when solving the Schrodinger equation used was DFT - B3LYP, this is a commonly used method that gives good short range electron correlation and is vastly superior to faster methods such as a simple restricted Hartree-fock.

The basis set essentially determines the accuracy of the calculation at the cost of the power and time required. The basis set used was LanL2MB. This is reported to be a medium level basis set that uses D95V on first row atoms but Los Alamos ECP on heavier atoms. ECP standing for effective core potential which approximates the non-valence electrons as they are unlikely to be involved in bonding. The basis sets typically revolve around the incorporation of multiple Gaussian functions to create the Slater type functions obtained from the Schrodinger equation. The higher number of functions used within the basis set for describing electronic structure (and polarizability) the more accurate picture that can be built up, however the longer the calculation.

An important point within the calculation was to maintain the same basis set and method for the frequency calculations as for the optimisation. This is because the approximations used will make no sense and will result in poor electron distributions and so called exicted electron density.

BCl3

The optimisation works through successive calculations of the Schroddinger equation using the Born Oppenhiemer approximation. The solution of a particular nuclear position is compared to the previous result and if a lower energy is reported the calculation proceeds down a potential well gradient. When a valley in the potential well is reached a minimum energy is obtained and the calculation terminates. This however can be a localised minima and not the optimised minimum energy structure.

A method for determining whether a minimum has been obtained is to determine the frequency analysis, which is the second derivative of the potential energy curve. A minimum of the potential energy curve gives a first derivative = 0 and the second derivative that is positive. All positive vibrational frequencies therefore is a good indication that a minima has been obtained. This however is not an indication that the absolute minima has been reached as any localised minima would give all positive results.

Bonding:

Using gaussview the minimised B - Cl Bonds can be estimated at 1.87A this compares to an actual reported bond distance of 1.742A. This shows reasonable but not high correlation.

The Cl-B-Cl bond angle is given as 120^o and reported in literature also as 120^o. The D_3h point group which it has been restricted to with high tolerance (0.0001) requires a planer structure with 120^o bond angles.

Bonding however is an arbitrary thing and within Gaussview is defined by an internal distance requirement and therefore where bonds are too long they are not displayed.

This doesn't mean they don't exist, they are merely not drawn on the structure. A bond itself is not just described by a distance but by electron density, enthalpy required to separate atoms and electrostatic interactions. A typical representation involves the overlap of molecular orbitals. Overlap of same phases results in favourable interactions and overlap of opposite phases results in antibonding interactions.

The molecule was restricted to D_3h point group which is shown in the planer triangular structure showing a 2C₃ (120^o rotational axis), 3C₂ (perpendicular)(180^o rotational axis), σ_h (horizontal reflection plane), 2S₃ (improper rotations) 3σ_v (reflection plane through main rotational axis)

The calculation submitted to and ran using Gaussian 3 on HP laptop which took 2-3 minutes.

BH₃ Vibrations

A similar approach was taken with BH3 and vibrations were calculated.

The vibrational frequencies obtained were all positive, spectrum shown below:

The Important IR stretches are shown below:

IR Stretches BH3

No	Form	Freq	Infrared	Symmetry (D3h)		No	Form	Freq	Infrared	Symmetry (D3h)
1		1145.71	92.7	A"2		2		1204.66	12.4	E'
3		1204.66	12.4	E'		4		2592.79	0.0	A'1
5		2731.31	103.83	E'		6		2731.31	103.83	E'

There are 6-virbations recorded however only 3 peaks this because some peaks are degenerate appearing at the same energy i.e. 2&3, 5&6 that belong to E point group. Also perfectly symmetric peaks that show no electric dipole moment change do not appear in the IR spectrum and are not seen, such as peak 4

Molecular orbitals of BH₃

Optimisation methods followed by energy calculations using a B3LYP Method and 3-21G basis set and a full NBO (Natural Bond Orbital Analysis) predicted the molecular orbitals for BH₃. 3-21G which is a low level fast basis set available for many elements, the 3 being used for the core electrons and the valence electrons defined using 2 (two Gaussians) and 1.

These Orbitals can be compared to empirically derived qualitative MO's using point group symmetry and LCAO theory

The BH₃ MO Diagram can be generated from the H₃ fragment and Boron

Method:

• Defined axis
• Chemical Fragments known as H₃ and B
• The Point group of BH₃ is known to be D_3h. Appling the symmetry operators gave the symmetry labels.
• Relative orbital energies roughly predicted
• Combined elements of the same symmetry
• LCAO prediction
• Compare to calculated orbitals, same axis important

Below shows the resulting MO diagram with both the LCAO approach and computer generated orbitals.

When constructing the MO diagram a difficult choice was reached for the relative energies of 3a'₁ and 2e', S interactions are typically stronger but the a'₁ starts at lower energy. The calculation of the orbitals suggested that the a'₁ orbital was of higher energy and therefore was orientated as such.

The qualitative MO orbital diagram and the calculation showed high correlation, suggesting that the accuracy in the approximation of the LCAO and symmetry combing MO is quite high. The method however revolves around user choice on certain energy levels, and requires computational methods to assign the relative energies of the MO's created. This is shown well in the 3a'₁ 2e' conundrum.

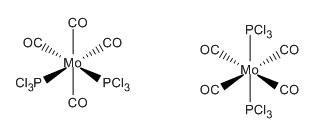
Isomers of Mo(CO)₄L₂

The vibrational spectra of a cis and trans isomers of Mo(CO)L₂ were investigated, where L=PPh₃. It is expected theoretically that they should give different numbers of vibrational bands associated with the carbonyl stretches. This is due to the symmetry of the stretch were IR spectrums don't show stretches with no change in dipole moment. The cis isomer should show 4 absorption bands where as the trans should only show 1.

To ease calculations the PPh₃ groups were replaced with PCl₃ that should have similar electronic contributions.

The procedure for obtaining the vibrational spectra:

• Loose optimisation using the B3LYP method and LANL2MB basis set to get rough geometry
• Torsion angle of PCl₃ adjusted to set angles so rotational profile will converge to correct minima:
  • Trans - Cl's eclipsed and eclipsing one CO
  • Cis - one Cl on each PCl₃ group parallel to axial CO but one up, one down (see images below)
• More exact reoptimisation using B3LYP method and LANL2DZ and ultfine parameters. (LANL2DZ a more accurate basis set)
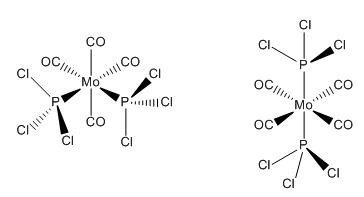
• This gave optimised structures (shown below)
• Frequency job carried out using B3LYP method and LANL2DZ (important to be same)
• All jobs run on high performance computer

Optimised structures

Cis Isomer	Trans Isomer
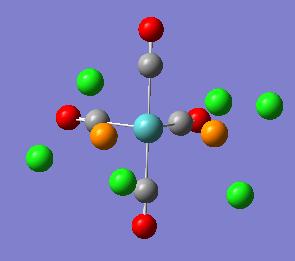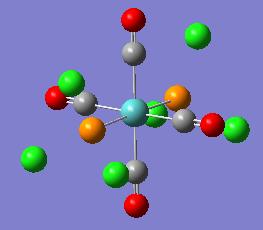
DOI:10042/to-4638	DOI:10042/to-4639

The optimisation removed the MO - P bonds this as before is due to gaussviews definition of bond (see earlier).

The geometry recorded shows a slight deviation from the dihedrals set so it is not quite eclipsing the carbonyls however the general form of the cis isomer with one Cl up on phosphorous 1 and down on phosphorous 2 remains the same. In both cases the chlorine remain 120^o away from each other. The trans structure also shows slight twisting away from the eclipised dihedral but not significant.

The Cis Structure gave a P-Mo-P angle 94.2^o and a Mo-P distance of 2.51A. The trans structure gave a P-Mo-P angle of 177^o and a Mo-P length 2.44A.

Literature sources report a slightly distorted octahedral geometry for the similar complexes cis-Mo(CO)₄(me₂Ph)₂ with P-Mo-P bond angle roughly 94.8^o and Mo-P bond distances of 2.53A. The trans (to P) C-O distances are reported as 1.98A and the cis (to P) 2.02A. These values correlate well to the modelling results. The structure however for the desired (but not modelled) Mo(CO)₄₍PPh₃)₂ is reported to have a much greater P-Mo-P angle of 104.6^o due to steric clash of the large phenyls

The energies reported from Gaussview are -623.58 a.u. for the cis isomer and -623.58 a.u. for the trans isomer. This suggests both isomers are equally stable. This implies that there is no steric interactions favouring one product over the other with only PCl₃.

The conversion of the cis isomer of Mo(CO)₄(PPh₃)₂ to the trans isomer is reported as facile with the trans isomer being the thermodynamic product by 2-3kcal

If the energies differed once converted to J/mol and dG calculated they could be used in equation 1 (below) to give the equilibrium constant. This assumes they can interconvert freely in a mixture, and should give the relative proportions using equation 2

A key inorganic technique is to be able to force an undesired conformation based on changing the ligand. Perhaps the trans isomer could be favoured by adding bulky substituent's to the phosphorous to cause steric repulsions. The original complex with L=PPh₃ involves bulky groups as suggested, which weren't taken into account in the calculation and probably its reasoning for thermodynamic stability.

Vibrations

All vibrations obtained were all positive which confirms the presence of the minima.

The spectrums observed are shown below:

IR Spectra

Cis	Trans

There are clear differences between the two isomers absorbance's particularly at 2000cm^-1 this is there area for CO stretches and shows that there are more modes active in the IR for the cis isomer due to the asymmetry in carbonyl stretches. This is best seen in the table below:

Vibrational results

Wavenumber cm-1	Trans	Cis
408 Mo-P
432 Mo-P	N/A
1950 C=O
2023 C=O	N/A

The IR of the metal-carbonyl's are reported to be 2000cm^-1 but down shifted towards 1900cm^-1 due to backbonding. These correlate well to the C=O stretches observed for the complex.

Analysis the 2023cm^-1 Cis CO stretches it can be seen that it results in a dipole change, were as for the trans isomer would result in no dipole change and therefore unseen. Similar effect for Mo - P stretches which is why less peaks at 400cm^-1 are observed

Mini Project

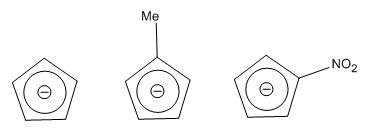
The mini-project carried out investigates the valence molecular orbitals of various cyclopentadiene ligands with both electodonating and electon withdrawing groups.

The molecular orbitals of an 18 electron Iron complex containing the cyclopentadiene ring derivatives were also compared to see how the bonding varied based on any differences in the MO's

Below are the structures of cyclopentadiene investigated:

These were then incorporated into an Iron complex as shown below:

The method used for the simple ligand calculations were DFT - B3LYP and a basis set of 6-31G(d) which is a fairly accurate basis set for first row atoms. The (d) allows for polerazibility within the molecule.

The method for the metal complexes was also DFT - B3LYP however a larger basis set to incorporate the d-orbitals had to be used. A rough optimisation was carried out using the LAN2MB basis set and then a more exact calculation used LAN2DZ (a more accurate basis set).

The optimisations of cp based ligands yields the below structures:

Optimised structures

Energy = -193.5 a.u. Bond Length = 1.41A	Energy = -232.8 a.u. Bond Length = 1.41A	Energy = -398.1 a.u. Bond Lengths = 1.43A, 1.38A
	DOI:10042/to-4640	DOI:10042/to-4641

Note a.u. are Hartrees where 1 a.u. = 2625.5 kJ/mol

Important to note that the structures are completely flat such that they can obey huckel's rules and be aromatic. The C-C bond lengths are also all identical for Cp and Cp-me however not for Cp-NO₂.

Molecular orbital anaylsis of cyclopentadiene ligands

Theoretical approximations for the aromatic cyclopentadiene ligands valence molecular oribitals can be made using LCAO theory.

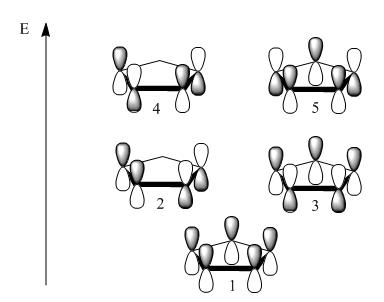
Below is the predicted orbitals and relative energies

Note that Ψ2 and Ψ3 are degenerate in the model as is Ψ4 and Ψ5.

Calculations yielded MO's that follow the LCAO predicted very well. (Once again showing the accuracy in qualitative approach to MO's). Shown below are the resultant orbitals using an isovalue of 0.04 which is good for discerning where the orbital contributions came from:

Calculated MO's Cyclopentadiene

-0.486	-0.344	-0.344	-0.122	-0.122

The degeneracy previously mentioned is also clearly present in the calculated MO's.

The molecular orbitals for the Cp-Me and Cp-NO₂ calculated are shown below:

It is clear that Ψ2 has electron density on the carbon next to the nitrogen in the CP-NO₂ however none next the methyl group in the Cp-Me. It can also be seen that Ψ3 has a differing electron density

Therefore it can seen that the group effects the electron density on particular carbons across the ring

A very interesting observation from the above MO Diagrams is that the Cp-Me shows no degeneracy, while the Cp-NO₂ reports degeneracy for Ψ2 and Ψ3 but not Ψ4 and Ψ5. This could be to do with the symmetry within the molecule. The Cp-NO₂ and Cp-me have C_2v symmetry but the Cp-Me has local C₃ symmetry in the methyl group that may cause the slight loss of degeneracy. Another interesting point is looking at the energies for Cp-Me only the full bonding Ψ1 is negative. For Cp all values are negative, and for Cp-NO₂ the first 3 orbitals are negative.

It can also been seen that electron density is clearly being pulled out of the ring on to the NO₂ This may account for the differing bond lengths.

The energies suggest that the NO₂ stabiles electrons in ring making it less reactive where as the Me destabilises electrons in ring making it more reactive

Complexed Ligands

The complex optimised structures:

Optimised structures

Energy = -558.6 a.u.	Energy = -597.9 a.u.	Energy = -763.0 a.u.
DOI:10042/to-4642	DOI:10042/to-4643	DOI:10042/to-4644

Note that the Me eclipses the Cl where as the NO₂ doesn't

Complex molecular orbitals

Theoretical LCAO can show which orbitals should interact with the CP ring, shown below:

The valence molecular orbitals are mainly consisted from overlap of the Fe d-orbitals with Ψ2 and Ψ3 as shown below:

Relevant MO's

MO	Cp-Fe	CpMe-Fe	FeCpNO2-Fe
HOMO - 2
HOMO
LUMO + 1

n.b. only relevant valence MO's that involve the Cp ring have been included in the analysis

An initial point is the clear overlap effects from the electron density of the chlorine in the valence orbitals and maybe a alkyl group would give a clearer MO distribution.

The molecular orbitals are spread over differing carbon groups, however the orbitals have similar shapes.

The important consequence of this however is the orientation of the methyl group above the Cl, where as in the Cp-NO₂ the NO₂ group is not eclipsing the Cl but a neighbouring carbon is. The orbitals are requiring certain overlap with the fixed d orbitals, but as mentioned before the electron withdrawing NO₂ shifts the Ψ2 and Ψ3 relative to the substituent, so when bonding occurs to the d orbitals a differing orientation is obtained.

Therefore using the MO overlap with the Fe d-obitals allows structural assignment on the attachment of the Cp Ring.

Vibrations

The vibrations of the molecules were all positive confirming a minima had been obtained. The infrared spectrum of the complex showed only 2 key peaks (1992 and 2026 cm^-1), an asymetric and symmetric carbonyl stretch:

IR Stretches

Spectrum	Symmetric	Asymmetric

The same peaks were evident in the Cp-NO₂ however also contained a C-N stretch at 1321.8cm^-1. The Cp-Me contained the same stretches but at 1947 and 1997 cm^-1.