Rep:Mod:dmc4
Physical Computational Chemistry Module 3, Experiment 3 Cope rearrangement
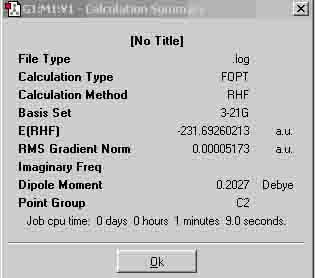
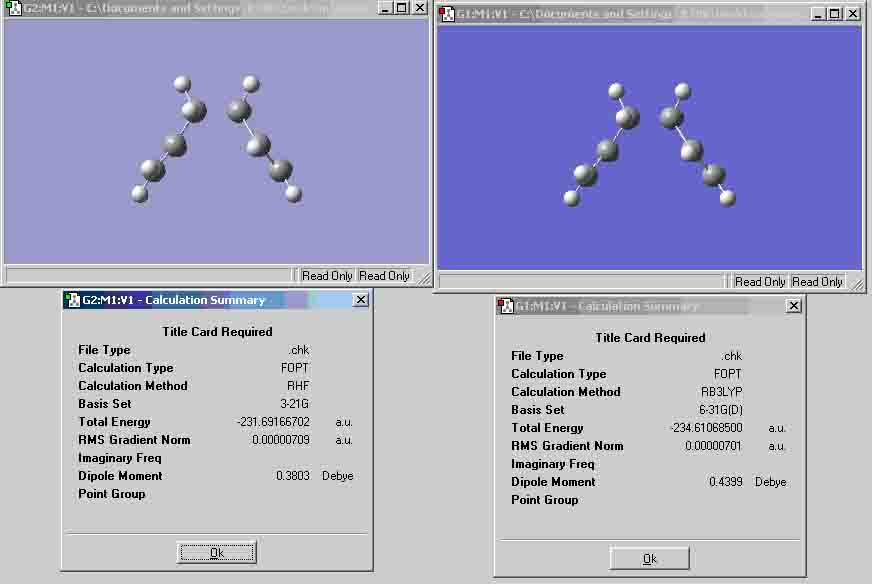
- 1,5-hexadiene ‘anti’ structure:
I would expect the ‘gauche’ structure’s final energy to be higher than that of the ‘anti’ structure’s final energy because there is steric hindrance with regard to the bond angle between the 2 alkene bonds.
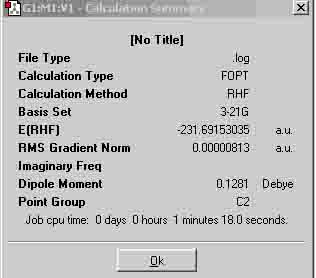
- 1,5-hexadiene ‘gauche’ structure:
| Structure | Final Energy (Hartrees) |
| Anti | -231.69260213 |
| Gauche | -231.69153035 |
| Structure | Point Group |
| Anti | C2 |
| Gauche | C2 |
Both molecules have a point group of C2. The results show that the anti has a more negative energy value, thus, the gauche conformation has a higher final energy value, which suggests that my prediction was correct. According to the appendix (1), I have optimised the molecules anti-1 and gauche-4.
- Lowest energy conformation of 1,5-hexadiene structure prediction:
- When compared to the structures in the appendix (1), my prediction looks similar to the anti-1 structure. The energies are similar but there are different point groups for each molecule, the predicted molecule has a C1 point group, whereas, the appendix molecule has a C2 point group.
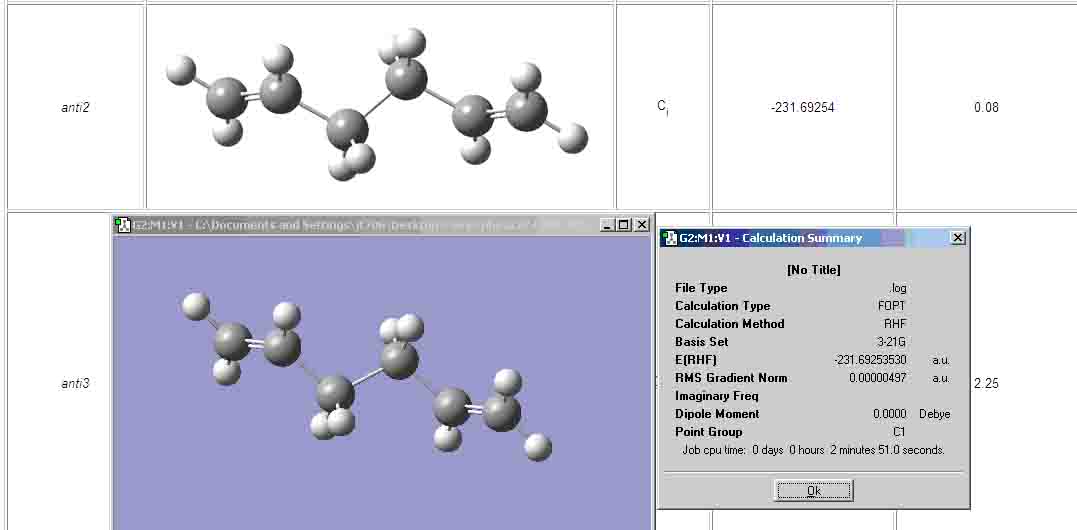
- Anti-2 conformation (Ci point group)
| Structure | Final Energy (Hartrees) |
| Anti-Ci (own) | -231.69253530 |
| Anti-Ci (appendix) | -231.69254 |
The molecule that I optimised is very similar to the one from the appendix. However, the point group is C1 as opposed to Ci. I tried rearranging the atoms in the molecule, but as you can see they look very similar, thus, I will continue to use the molecule shown in the picture as my Ci molecule.
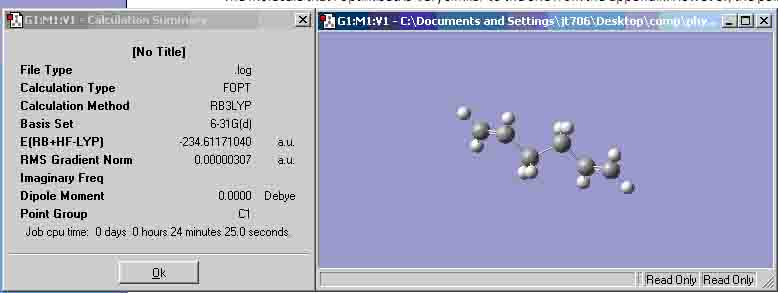
- B3YLP/6-31G calculation:
The geometry of the higher level calculation has not changed very much. However, there is a significant change in the final energy values as the new value is -231.6117040 Hartrees compared with the -231.69253530 Hartrees from the lower level calculation.
Sum of electronic and zero-point Energies= -234.469204
Sum of electronic and thermal Energies= -234.461858
Sum of electronic and thermal Enthalpies= -234.460913
Sum of electronic and thermal Free Energies= -234.500776
Experimental energies
Summary of energies (in hartree)
| Chair TS | ||||||||||||||||||||||||
| Boat TS | ||||||||||||||||||||||||
| Reactant anti2 |
Optimizing the "Chair" and "Boat" Transition Structures (a)-(d) On the left is the chair transition state that was optimised using the Berny optimisation. On the right is the chair transition state that was optimised using the frozen co-ordinate optimisation.
As the table shows, the frozen co-ordinate optimisation has more realistic bond distances for the bond formation and bond breaking. The Berny optimisation has distances that are similar. This could suggest that the Berny optimisation would show the molecule before it entered the transition state and the frozen co-ordinate optimisation would show the molecule as it was about to leave the transition state. (e) For some reason the boat calculation did not fail and the reason behind this I do not know. I had all the atoms numbered exactly the same as the wiki page (even the hydrogens) but the calculation did work. Whether this is relevant or not is not determinable.
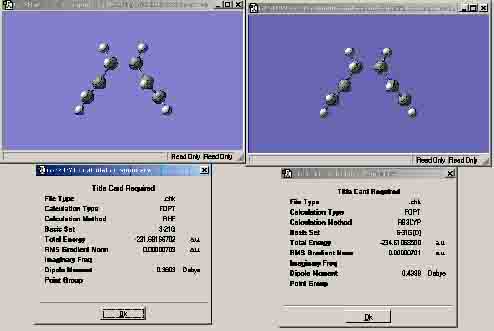
Chair transition state: left = 3-21G level; right = 6-31G (d) level This is the chair transition state optimised via the Berny optimisation technique. As you can see from the energies, the 3-21G energy IRC optimisation has a very similar energy to the Berny optimisation (a difference of 0.00000001H). However, the 6-31G IRC optimisation shows quite a large energy difference to the Berny optimisation energy. This could suggest that the 6-31G IRC optimisation is closer to being the transition state of the molecule than the other optimisations. However, due to the inaccuracy of the optimisation choice, this might not be the minimum of the transition state and this just could be one of many minimums that are present in the reaction pathway.
Chair transition state: left = 3-21G level; right = 6-31G (d) level Both sets of transition states show that the 6-31G optimisation shows a more negative total energy value. Moreover, both the 3-21G optimisations and the 6-31G optimisations have energies that are close to each other.
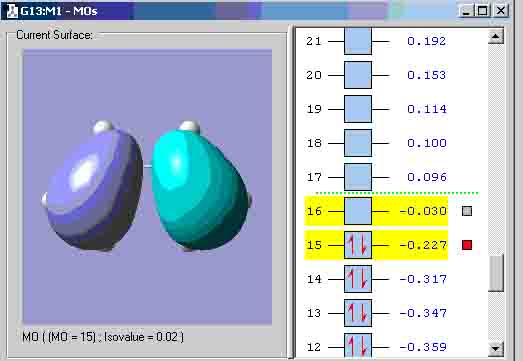
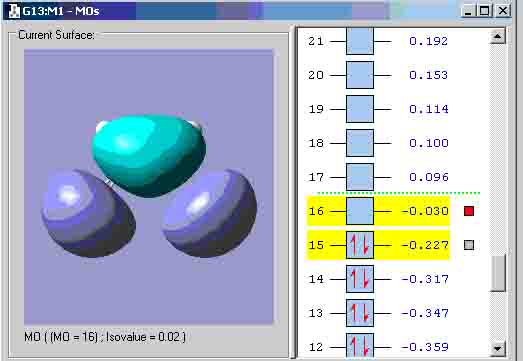
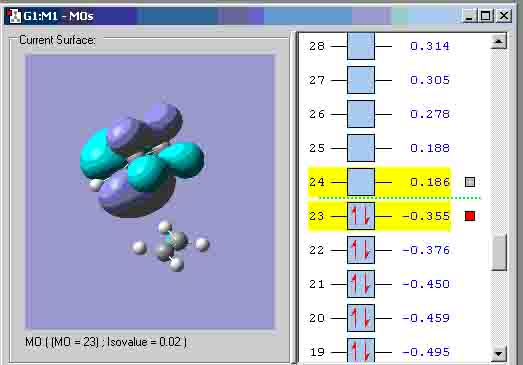
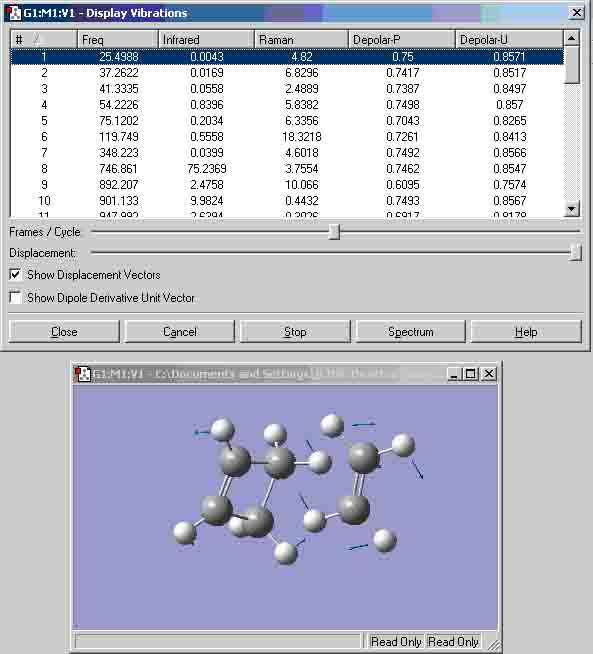
I used the zero point vibrational energy as the 6-31G optimisation activation energy. The table shows that the values between the experimental and computational activation energies are greatly different. This suggests that my computational transition states structures could have been incorrect. Diels alder cycloaddition Cis-butadiene HOMO: Symmetry with respect to plane = anti-symmetric. Cis-butadiene LUMO: Symmetry with respect to plane = symmetric. I attempted to create the transition state the same way that the boat transition state was created (the Q2TS calculation) but I got the structure below that could not show any MO’s, therefore, I had to create the transition state with the method used to create the chair transition state. Transition state: Transition state HOMO: Symmetry with respect to plane = symmetric. Transition state LUMO: Symmetry with respect to plane = anti-symmetric. Geometry and bond lengths of partly formed C-C sigma bonds: Bond lengths of partly formed C-C sigma bonds: 4.14872A and 4.31774A. The vibration that demonstrates the reaction pathway for the transition state is shown below: The bond formation seems to be asynchronus.
The HOMO at the transition state appears to be symmetric or “s”. Exo maleic energy
Exo maleic energy: -688.71418400H Endo maleic energy: -688.64873554H This shows that the exo configuration had more energy than the endo configuration, thus, less stable. This could be due to the strain from the two sections of the cyclic molecule that are close together, ie the parts that are pointing in the same direction. The endo structure has the oxygen groups pointing in the opposite direction to the bridging carbons, whereas, the exo structure has both groups pointing the same way. Ran out of time for the rest of the exercise. |