Rep:Mod:dmc3
Computational Inorganic Chemistry
Optimised B-Cl bond length = 1.86512 A
Optimised Cl-B-Cl bond angle = 120 degrees
File type = .log
Calculation type = FOPT
Calculation method = RB3LYP
Basis set = LANL2MB
Final energy = -69.43928112 au
Dipole moment = 0 Debye
Point group = D3H
Time for calculation to take place = 11 secs
Own molecule = H2O (http://hdl.handle.net/10042/to-1027)
Center Atomic Atomic Coordinates (Angstroms)
Number Number Type X Y Z
---------------------------------------------------------------------
1 8 0 0.000000 0.000000 0.000000
2 1 0 0.000000 0.000000 0.960000
3 1 0 0.904936 0.000000 -0.320455
Bond distance (H-O) = 1.02717 A
Bond angle (H-O-H) = 97.186degrees
Calculation type= FOPT
Calculation method = RB3LYP
Basis set = LANL2MB
Final energy = -75.32277388 au
Dipole moment = 1.5936 Debye
Point group = C2V
Time for calculation to take place = 16 secs
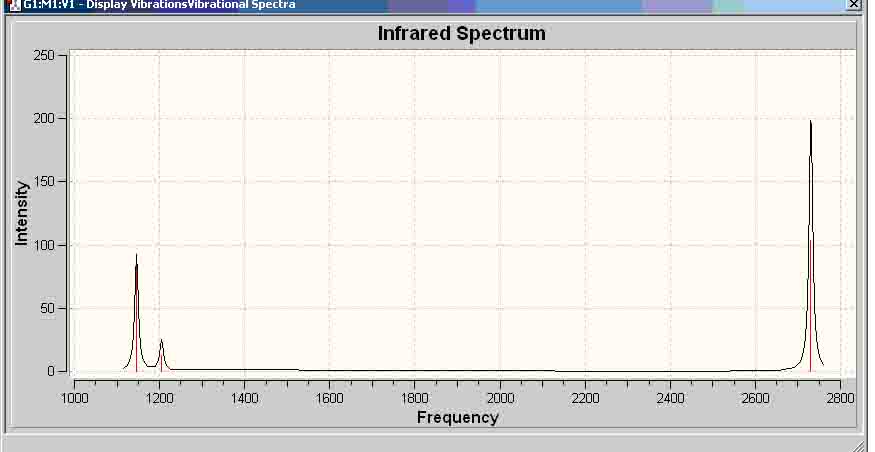
Vibrational analysis and confirming minima
| BH3 optimisation | Calculation type | FOPT |
| Calculation method | RB3LYP | |
| Basis set | 3-21G | |
| Final energy | -26.46226436 au | |
| Dipole moment | 0 D | |
| Point group | D3H | |
| Calculation time | 10 secs | |
| BH3 frequency | Calculation type | FREQ |
| Calculation method | RB3LYP | |
| Basis set | 3-21G | |
| Final energy | -26.46226436 au | |
| Dipole moment | 0 D | |
| Point group | C3H | |
| Calculation time | 9 secs |
Animating the vibrations
| No. | Form of vibration | Frequency | Intensity | Symmetry D3h point group |
| 1 | 
All H atoms move backwards and forwards perpendicular to the plane, B atom moves in opposite direction to H atoms. |
1145.9 | 92.6789 | A’’2 |
| 2 | 
One H atom and B atom remain fixed but move up and down together; other two H atoms come together and away from each other. |
1204.78 | 12.3867 | E’’ |
| 3 | 
B atom rocks from side to side, all three H atoms move, two towards each other and away, the other from side to side. |
1204.78 | 12.3892 | E’’ |
| 4 | 
B atom is stationary, all three H atoms move in and out. |
2592.11 | 0 | A’1 |
| 5 | 
One H atom is fixed, the other two move towards and away from the B atom (which moves towards the H atom going towards it) in opposite directions. |
2730.57 | 103.849 | E’ |
| 6 | 
One H atom moves up and down towards the B atom, which moves towards and away from it. The other two H atoms move towards and away from the B atom in the same direction. |
2730.57 | 103.842 | E’ |
Even though there are 6 vibrations, only 3 peaks appear because there are 2 sets of redundant vibrations (i.e. each pair of vibrations vibrate at the same frequency), and thus, would not show two peaks as the vibration with the higher intensity would overshadow the other. Also, one of the vibrations has an intensity of 0, hence, it would not show in the IR spectrum.
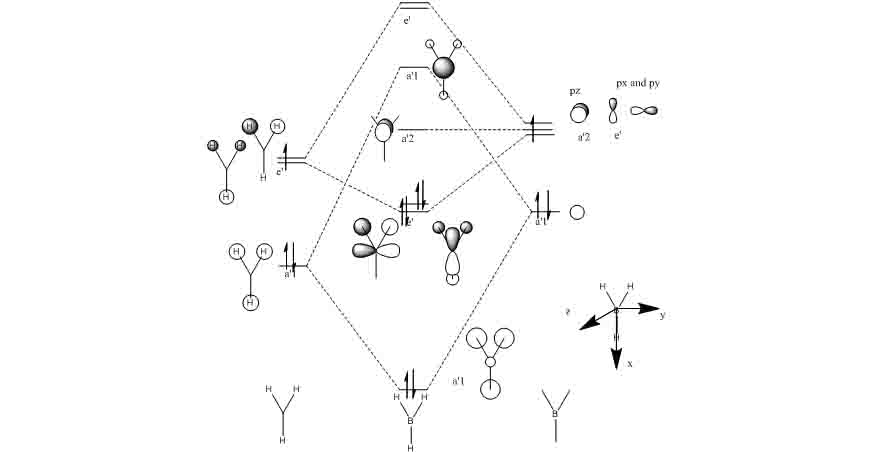
Molecular orbitals of BH3
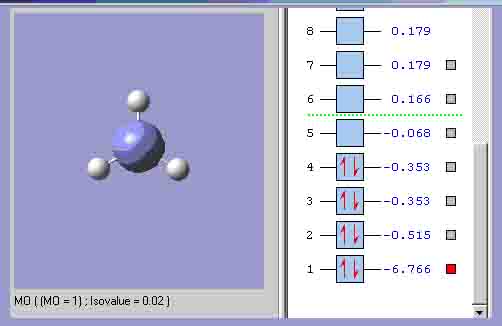MO1, which is the equivalent of the highest energy a’1 orbital.
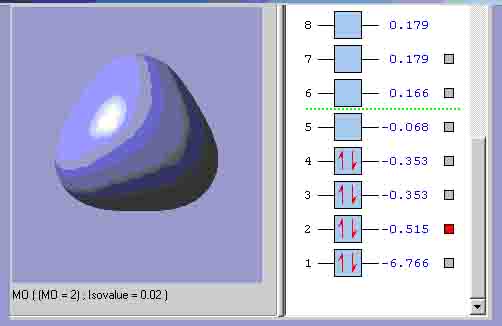MO2, which is the equivalent of the lowest energy a’1 orbital.
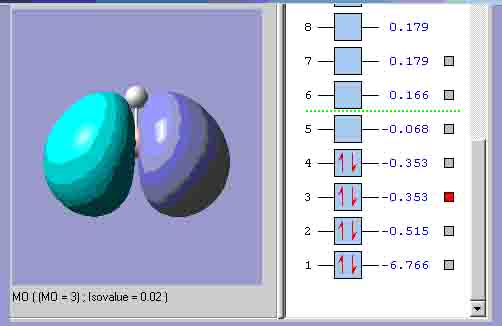MO3, which is the equivalent of one of the lowest energy e’ orbitals.
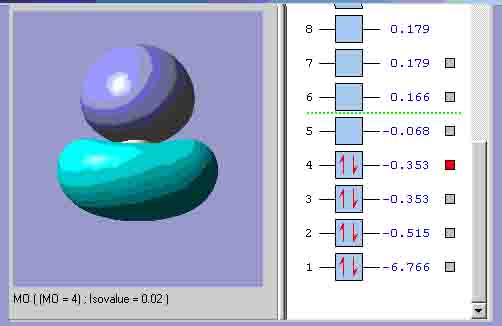MO4, which is the equivalent of the other lowest energy e’ orbital.
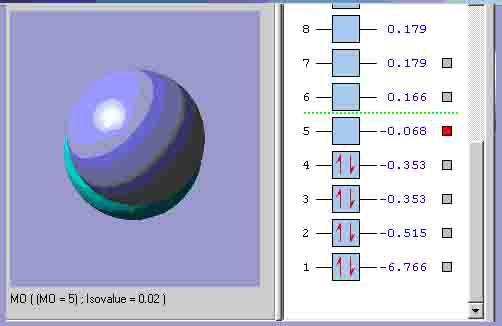MO5, which is the equivalent of the pz orbital.
This shows that the qualitative MO theory has a high accuracy and it is very useful in predicting the quantitative molecular orbitals of molecules.
Part 2
Optimised geometry
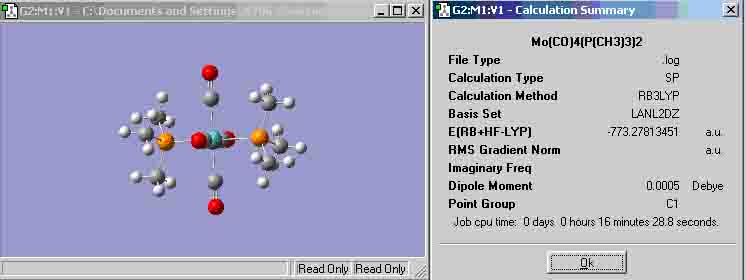
Trans Mo(CO)4(P(CH3)3)2 (http://hdl.handle.net/10042/to-1042)
4(P(CH3)3)2.jpg){kind=spacer}
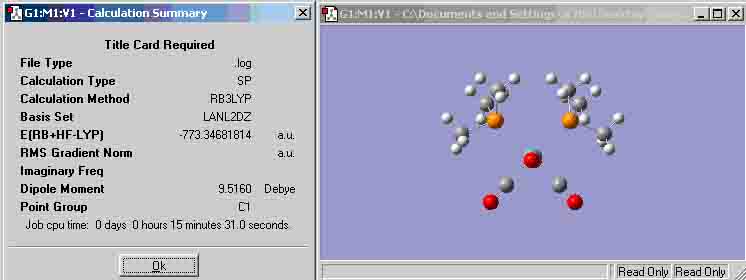
Cis Mo(CO)4(P(CH3)3)2 (unable to publish)
4(P(CH3)3)2.jpg)
Trans energy – Cis energy = energy difference
-773.2781351H - -773.34681814H = 0.0686836H x 2625.5KJ/mol = 180.3287918KJ/mol.
The cis conformation has a higher final energy than the trans conformation, thus, it is less stable.
All bond angles in the Trans molecule with the Mo as the second atom (i.e. in the middle of the angle) are 90 degrees.
Trans P-C-H bond angle = 109.471 degrees
For the atoms in the Trans molecule, the bond lengths and angles seem to be the same for each species (i.e. every Mo-C bond is the same length), however, this is not the same case for the cis molecule, thus, the bond lengths below for the cis molecule are the mean values. This may have occurred because there was something wrong with the initial file or process when optimising the molecule (which could also explain why it is unable to publish the optimisation) or it could be because the two cis groups are quite large, therefore, they strain the molecule to have bond lengths and angles that are not the same as the trans molecule.
Cis P-C-H bond angle = 108.912 degrees
Cis X-Mo-X bond angle (X = C/P) = 89.5314 degrees
Literature compound is Mo(CO)4(PPh3)2.
| Bond | Calculated Trans bond length (A) | Calculated Cis bond length (A) | Literature Trans bond length (A) | Literature Cis bond length (A) |
| Mo-C | 2.06000 | 2.00722 | 2.011 | 2.007 |
| Mo-P | 2.39000 | 2.648105 | 2.500 | 2.5765 |
| C=O | 1.25840 | 1.18983 | 1.1645 | - |
| P-C | 1.87000 | 1.892355 | 1.841 | - |
| C-H | 1.07000 | 1.095263 | - | - |
When comparing the literature and calculated values, it can be seen that there are similarities between the two sets of values. It also shows that the average bonds in the cis conformation of the calculated molecules has results close to that of the experimental values, which could suggest the the calculated cis compound could be correct.
Nevertheless, the calculated cis compound could be wrong, as the bond lengths between same atom types varies between each bond, when it is probable that the bond lengths should not vary, however, due to the cis structure being sterically strained, it may be possible to have varying bond lengths. The cis compound was created 3 different times in the Gaussview program, with each result ending the same, thus, if the cis molecule is incorrect it can be concluded that either the method of producing the molecule is wrong or the program cannot create a cis conformation of the molecule.
IR analysis
Trans Mo(CO)4(P(CH3)3)2 (http://hdl.handle.net/10042/to-1040)
Cis Mo(CO)4(P(CH3)3)2 (http://hdl.handle.net/10042/to-1041)
Table of Major peaks
| Bond type | Calculated peak (cm-1) | Experimental peak (cm-1) |
| Trans | 1017 | 1020 |
| Trans | 1839 | 1891 |
| Cis | 1018 | 1012 |
| Cis | 1027 | 1040 |
| Cis | 1850 | 1863 |
| Cis | 1870 | 1887 |
| Cis | 1960 | 1968 |
Again, the calculated and experimental values are similar, thus showing that the calculate approach to an experiment is a very good prediction of the products in a reaction.
Ammonia
Symmetry
NH3
Long bond NH3
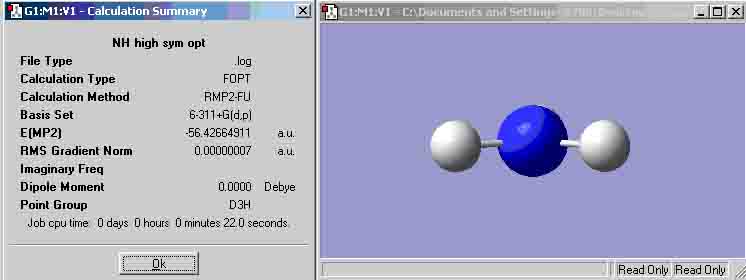
High symmetry NH3
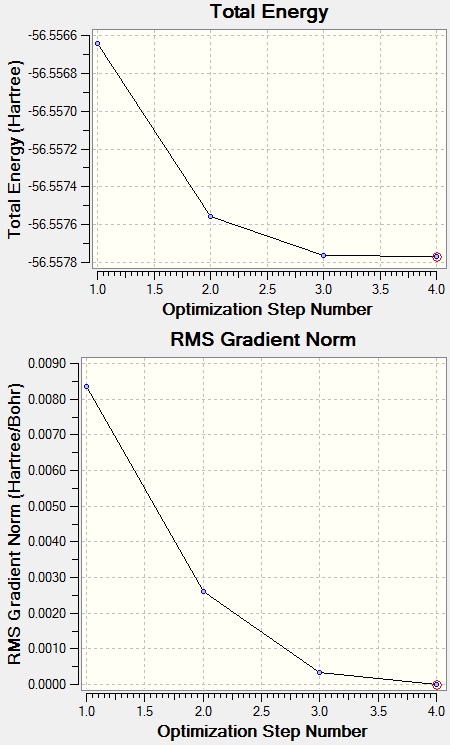
The high symmetry structure has changed the ammonia molecule into a planar structure. The time taken to optimise the high symmetry ammonia was quicker than the two previous structures. The symmetry doesn’t seem to affect the time for the calculation to take place. D3h is the most symmetrical point group and has the shortest time, but C3v was the second most symmetrical group but had the longest calculation time. Symmetrical molecules can break symmetry if the optimisation provides a more stable molecule.
Lowest energy optimisation: -56.41530842 au = 148118.3923 KJ/mol
Energy differences:
-56.41530857 - -56.41530842 = -0.00000015 au = -3.93825xE-4 KJ/mol
-56.42664911 - -56.41530842 = -0.01134069 au = -29.775 KJ/mol
The energy differences are significant because they show that by slightly altering the molecules structure can affect the overall energy of the molecule and it’s point group, thus, its symmetry.
Methods
| Calculation Method | Calculation time (secs) |
| NH3 6-31G | 33.0 |
| NH3 MP2 | 38.0 |
| High Sym NH3 6-31G | 16.0 |
| High Sym NH3 MP2 | 22.0 |
The higher level calculations take 5 seconds and 6 seconds longer than the lower level calculations.
MP2 calculation energy
ΔE=E(D3h)-E(C3v)
ΔE=-56.42664911 - -56.41530857 = -0.01134054 a.u. = -29.775 KJ/mol.
6-31G calculation energy = -56.56066276 - -56.56698509 = 6.32233xE-3 a.u. = 16.5993 KJ/mol.
This calculation shows that the energy difference between the two calculation methods is large, especially with the lower level calculation providing a positive energy, which would be incorrect. The value of -29.775 KJ/mol for the MP2 calculation is close to the experimentally determined value of -24.3 KJ/mol, but obviously there must be something missing from the calculation that is present in the experimental.
Inversion Mechanism
Ammonia vibrational analysis
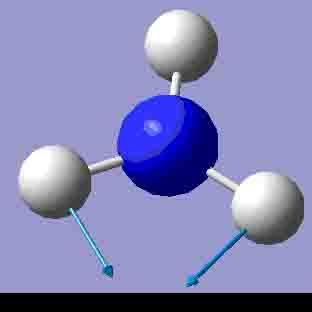
| C3v NH3 frequency (cm-1) | C3v NH3 vibrations | D3h NH3 vibrations | D3h NH3 frequency (cm-1) |
| 999.413 | 
|
|
-766.722 |
| 1673.65 |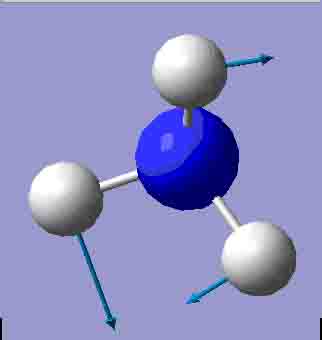 
|
|
1576.99 |
| 1673.65 |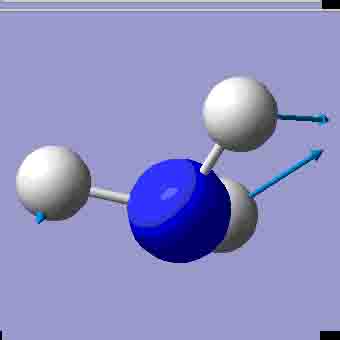 
|
|
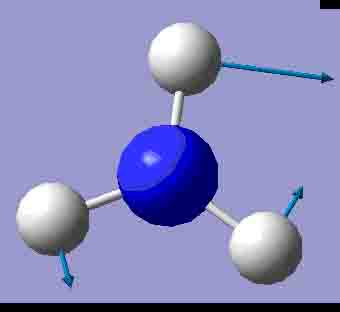
1576.99 |
| 3484.88 | 
|
|
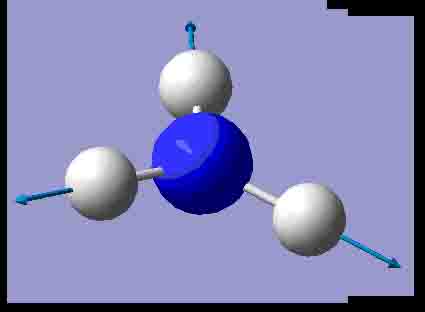
3623.13 |
| 3627.94 | 
|
|
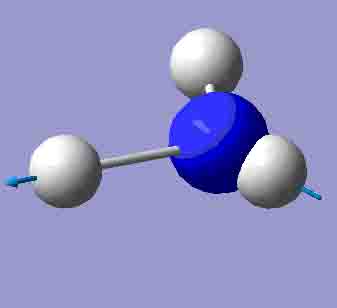
3841.51 |
| 3627.94 |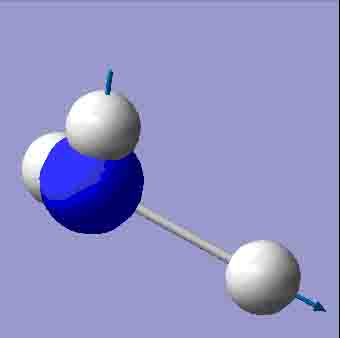 
|
|
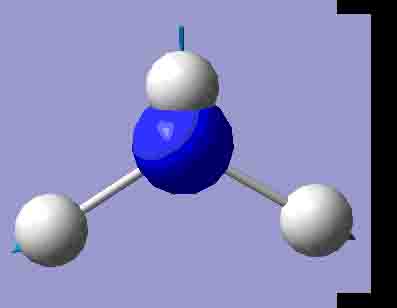
3841.51 |
C3v NH3 IR
D3h NH3 IR
There are 6 positive frequencies for the C3v NH3 molecule, but only 5 for the D3h molecule. It has one negative frequency which is -766.722cm-1. The first vibrations in the table seem to follow the inversion mechanism, because the hydrogens move in such a way that if they had more energy, they would be able to invert the ammonia molecule.
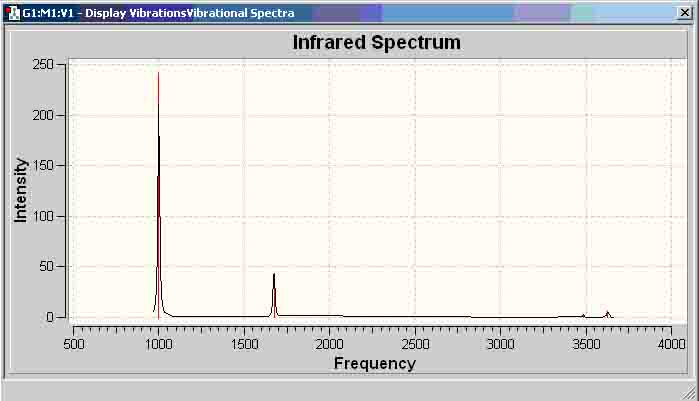
| Stretch/bend | Calculated (cm-1) | Experimental (cm-1) |
| N-H symmetric stretch | 3484.88 | 3534 |
| N-H asymmetric stretch | 3627.94 | 3464 |
| N-H asymmetric stretch | 3627.94 | 3464 |
| H-N-H bend | 1673.65 | 1765 |
| H-N-H bend | 1673.65 | 1765 |
| H-N-H bend | 999.413 | 1139 |
Mini Project:
Fuels of the future
Staggered conformation (http://hdl.handle.net/10042/to-1098 )
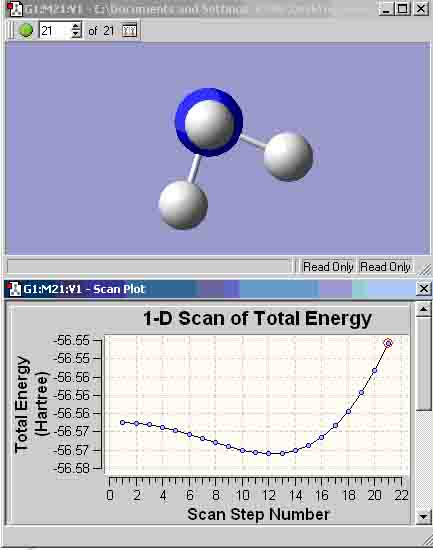
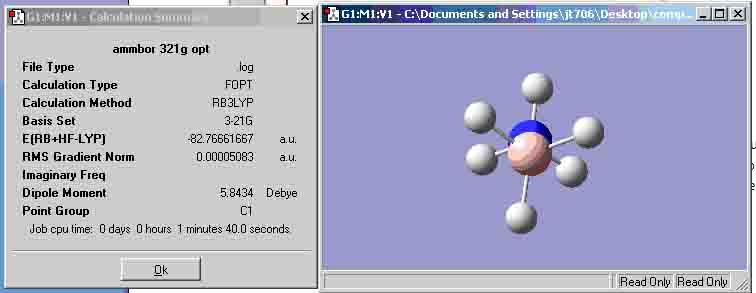
Ammonia-Borane optimisation (B3LYP 3-21G)
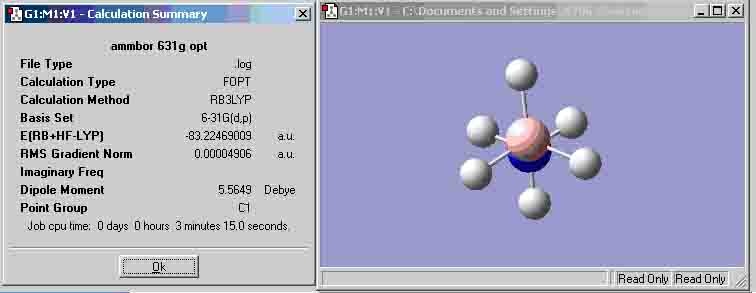
Ammonia-Borane optimisation (B3LYP 6-31G)
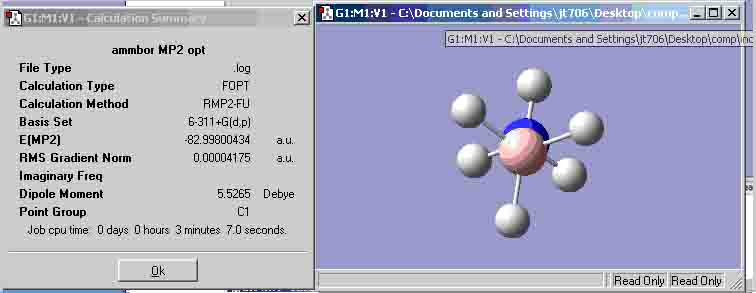
Ammonia-Borane optimisation (MP2 6-311+G(d,p))
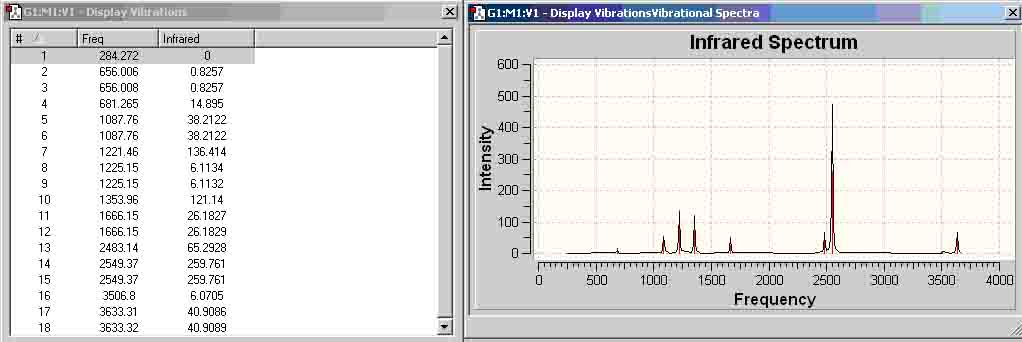
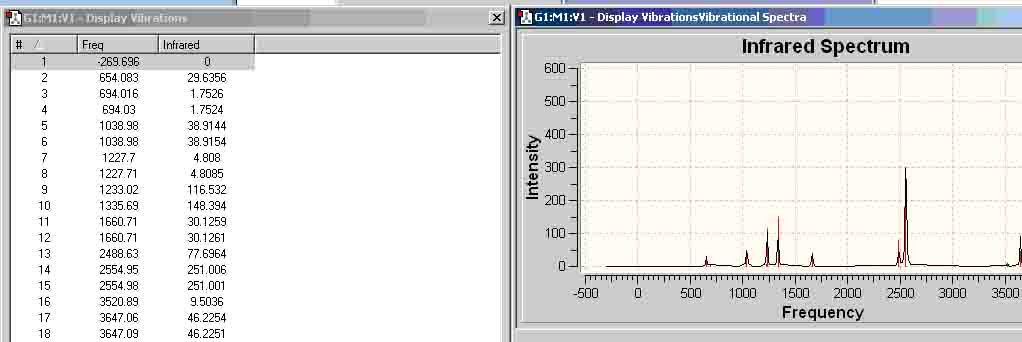
Ammonia-Borane Infrared (MP2 6-311+G(d,p))
Eclipsed conformation
Ammonia-Borane optimisation (B3LYP 3-21G)
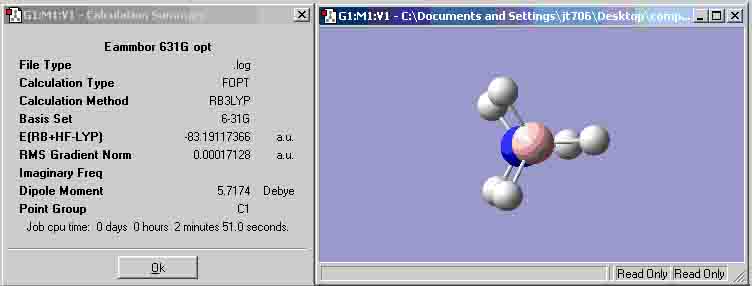
Ammonia-Borane optimisation (B3LYP 6-31G)
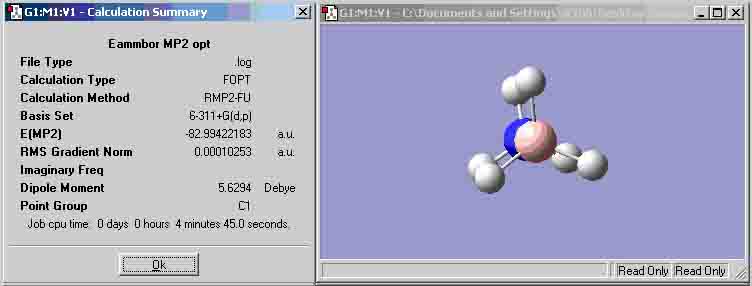
Ammonia-Borane optimisation (MP2 6-311+G(d,p))
Ammonia-Borane Infrared (MP2 6-311+G(d,p))
Ethane staggered
Ethane eclipsed
| Calculation Method | Staggered conformation energy (H) | Eclipsed conformation energy (H) |
| (B3LYP 3-21G) | -82.76661667 | -82.76331994 |
| (B3LYP 6-31G) | -83.22469009 | -83.19117366 |
| (MP2 6-311+G(d,p)) | -82.99800434 | -82.99422183 |
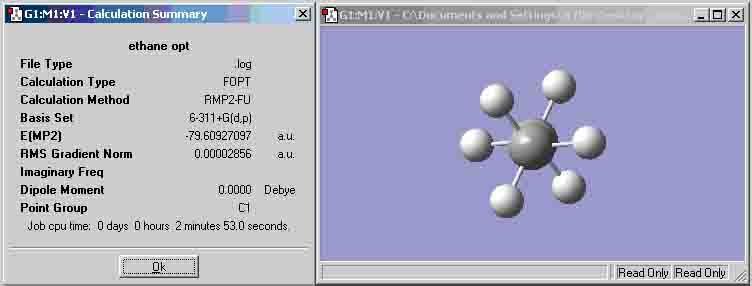
| Ethane (MP2 6-311+G(d,p)) | -79.60927097 | -79.80850664 |
The results show that the median value for the energies is from the MP2 calculation method, thus, it would appear that this is the most accurate of the three calculation types and will be used for further calculations. According to the results from the table, in each comparable case, the eclipsed conformation appears to have a lower energy than its staggered counterpart, albeit, only by a small quantity. When compared to ethane, the ammonia-borane has a slightly higher energy, and with ethane it is the staggered conformation that has the lower energy.
Ethane has a covalent bond that has each carbon atom donating an election to create a σC-C single bond. With ammonia-borane, the boron atom is electron deficient (it has 6 electrons in its valent shell, 8 electrons are needed to be stable), therefore, the nitrogen atom donates one of its lone pairs into the vacant p orbital of the boron to create a dative covalent σN-B single bond.
This makes the ammonia part of the molecule more acidic and the borane part of the molecule more basic. This means that the ammonia-borane is prone to have strong intermolecular dipole-dipole interactions, which is why it has a melting point of approximately 110°C. Since ethane is not prone to having strong dipole-dipole interactions, only weaker Van der Waals forces, ethane has a melting temperature of approximately 89.87K, which is 183.13°C.
NH4Cl + NaBH4 -> NH4BH4 + NaCl
NH4BH4 -> H2 + NH3BH3
Relatively speaking, NaCl is the most stable molecule as it has a melting point of 801°C. Sodium borohydride has a melting point of less than 300°C (decomposed) and ammonium chloride has a melting point of 340°C (before it sublimes). The high melting temperature of NaCl shows that the compound has strong bonds, and therefore, it could be suggested that the formation of these bonds is the driving force of the reaction. Ammonia-borane would have to be more stable than the NH4BH4 compound because there is the formation of hydrogen gas, which is then liberated acting as the driving force of the decomposition.
References:
http://www.ucl.ac.uk/~uccaati/Energy.html
The Heat Capacity of Ethane from 15K to the Boiling Point.
The Heat of Fusion and the Heat of Vaporization
BY R. K. WITT~AN D J. D. KEMP
Ammonium chloride
Corp MSDS 1 (1), 233:D / IR-Spectra (3), 1521:D / RegBook 1 (3), 3325:H / Sax 6, 260 / Sigma FT-IR 1 (2), 1012:C
Sodium chloride
Aldrich MSDS 1, 1608:C / Corp MSDS 1 (2), 3135:D / RegBook 1 (3), 3319:F / Sax 6, 2419
Sodium borohydride
Aldrich MSDS 1, 1608:B / Corp MSDS 1 (2), 3132:B / Corp MSDS 1 (2), 3133:C / Corp MSDS 1 (2), 3132:A / Corp MSDS 1 (2), 3132:C / IR-Spectra (3), 1534:G / RegBook 1 (3), 3261:F / RegBook 1 (3), 3261:E / Sax 6, 2414
Synthesis of ammonia borane for hydrogen storage applicationsDavid J. Heldebrant, Abhi Karkamkar, John C. Linehan and Tom Autrey
Ir ammonia