Rep:Mod:dk27102

Cope Rearrangement Tutorial

In this exercise, we looked at the various conformations of 1, 5-hexadiene, as well as methods of computationally analysing the transition states in a Cope Rearrangement

Hexadiene Anti-Periplanar Conformation

Optimisation parameters:

Method

Method	Ground State	Hartree-Fock	Default Spin
Basis Set	3-21G
Charge	0	Spin	Singlet
Memory Limit	250 MB

File:HexadieneAPPOpt.LOG

Summary of Hexadiene Anti-Periplanar Conformation Optimisation

File Name	HexadieneAPPOpt
File Type	.log
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
Total Energy	-231.69260 a.u.
RMS Gradient Norm	0.00001296 a.u.
Dipole Moment	0.2021 Debye
Point Group	C2
Job cpu time	0 days 0 hours 0 minutes 15.0 seconds

The point group was altered to be C2 (from C1) through the "symmetrize" function. However this didn't change the molecule drastically and was merely loosening the parameters for symmetry.

Hexadiene Gauche Conformation

Optimisation parameters:

Method

Method	Ground State	Hartree-Fock	Default Spin
Basis Set	3-21G
Charge	0	Spin	Singlet
Memory Limit	250 MB

File:HexadieneAPPOpt.LOG

Summary of Hexadiene Gauche Conformation Optimisation

File Name	HEXADIENEGAUCHEOPT
File Type	.log
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
Total Energy	-231.68772 a.u.
RMS Gradient Norm	0.00002136 a.u.
Dipole Moment	0.4559 Debye
Point Group	C2
Job cpu time	0 days 0 hours 0 minutes 36.0 seconds

The point group was altered to be C2 (from C1) through the "symmetrize" function. However this didn't change the molecule drastically and was merely loosening the parameters for symmetry. The conformation's energy is higher than the anti-conformation because the alkene groups are much closer and clash.

Hexadiene Lowest Energy Conformation

In order to find the lowest energy conformation of 1,5-hexadiene, it must be between the gauche-1 and anti-1 conformations. Drawing it in the gauche-3 conformation seemed like a sound proposal, which was proved to be correct.

Optimisation parameters:

Method

Method	Ground State	Hartree-Fock	Default Spin
Basis Set	3-21G
Charge	0	Spin	Singlet
Memory Limit	250 MB

File:HEXADIENEGAUCHE3OPT3.LOG

Summary of Hexadiene Lowest Energy Conformation Optimisation

File Name	HEXADIENEGAUCHE3OPT3
File Type	.log
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
Total Energy	-231.69266 a.u.
RMS Gradient Norm	0.00000422 a.u.
Dipole Moment	0.3407 Debye
Point Group	C1
Job cpu time	0 days 0 hours 0 minutes 11.0 seconds

To prove this, all other conformations of 1,5-heaxadiene were computed.

Conformation of Hexadiene.

Conformer	Structure	Point Group	Energy/Hartrees	Relative Energy/kcal/mol	Log File
Gauche 1		C2	-231.68772	3.10	File:HEXADIENEGAUCHEOPT.LOG
Gauche 2		C2	-231.69167	0.62	File:HEXADIENEGAUCHEOPT.LOG
Gauche 3		C1	-231.69266	0.00	File:HEXADIENEGAUCHEOPT.LOG
Gauche 4		C2	-231.69153	0.71	File:HEXADIENEGAUCHEOPT.LOG
Gauche 5		C1	-231.68962	1.91	File:HEXADIENEGAUCHEOPT.LOG
Gauche 6		C1	-231.68916	2.2	File:HEXADIENEGAUCHEOPT.LOG
Anti 1		C2	-231.69260	0.04	File:HEXADIENEGAUCHEOPT.LOG
Anti 2		Ci	-231.69254	0.08	File:HEXADIENEGAUCHEOPT.LOG
Anti 3		C2h	-231.68907	2.25	File:HEXADIENEGAUCHEOPT.LOG
Anti 4		C1	-231.69097	1.06	File:HEXADIENEGAUCHEOPT.LOG

As we can see, the gauche-3 conformation is the lowest energy conformation of 1,5-hexadiene.

Hexadiene Anti-2 Conformation

3-21G Basis Set

Optimisation parameters:

Method

Method	Ground State	Hartree-Fock	Default Spin
Basis Set	3-21G
Charge	0	Spin	Singlet
Memory Limit	250 MB

File:HEXADIENEOPTANTI22.LOG

Summary of Hexadiene Anti-2 Conformation 3-21G Optimisation

File Name	HEXADIENEOPTANTI22
File Type	.log
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
Total Energy	-231.69254 a.u.
RMS Gradient Norm	0.00005147 a.u.
Dipole Moment	0.0001 Debye
Point Group	C1
Job cpu time	0 days 0 hours 0 minutes 11.0 seconds

6-31G Basis Set

Method

Method	Ground State	Hartree-Fock	Default Spin
Basis Set	6-31G (d)
Charge	0	Spin	Singlet
Memory Limit	250 MB

File:Log 67295.log

Summary of Hexadiene Anti-2 Conformation 6-31G Optimisation

File Name	Log_67295.log
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G
Charge	0
Spin	Singlet
Total Energy	-234.61171035 a.u.
RMS Gradient Norm	0.00001437 a.u.
Dipole Moment	0.0000 Debye
Point Group	C1
Job cpu time	0 days 0 hours 1 minutes 46 seconds

As we can see, the structure or geometry of the molecule has not changed at all (ie the shape of the potential energy surface is very similar). However the energy is lower that is because the potential energy surface is lower in energy. This is because the larger 6-31G basis set has more terms. Hence it is more accurately able to characterise the core orbitals, the 1s non bonding orbitals on the C.

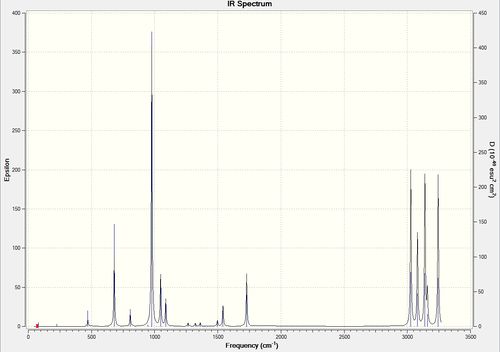
Frequency Calculation of 6-31G Optimised Anti-2 Conformation

A frequency calculation of the above was carried out. The following shows that an energy minima was indeed found, as there are no negative frequencies and the top line is within ±15cm^-1

File:HEXADIENEOPTANTI2 631GFREQ.LOG

 Low frequencies ---   -9.3747   -0.0006    0.0004    0.0008    3.6336   13.2052
 Low frequencies ---   71.9000   79.9127  116.8623

Electronic Energies:

Thermochemistry Analysis

Sum of electronic and zero-point Energies	-234.46920 a.u.	Potential energy at 0K, including zero-point energy. E = Eelec + ZPE.
Sum of electronic and thermal Energies	-234.461857 a.u.	Potential energy at 298.15 K and 1 atm including contributions from the translational, rotational, and vibrational energy modes E = E + Evib + Erot + Etrans).
Sum of electronic and thermal Enthalpies	-234.460913 a.u.	Potential energy at 298.15 K and 1 atm including additional correction for RT (H = E + RT).
Sum of electronic and thermal Free Energies	-234.500777 a.u.	Potential energy at 298.15 K and 1 atm including additional entropic contribution to the free energy (G = H - TS).

Chair Transition State

Allyl Fragment Optimisation

An allyl fragment was created and optimised in order to make the two halves of a transition state.

Optimisation parameters:

Method

Method	Ground State	Hartree-Fock	Default Spin
Basis Set	3-21G
Charge	0	Spin	Singlet
Memory Limit	250 MB

File:FRAG321GOPT.LOG

Summary of Allyl Fragment 3-21G Optimisation

File Name	FRAG321GOPT
File Type	.log
Calculation Type	FOPT
Calculation Method	UHF
Basis Set	3-21G
Charge	0
Spin	Doublet
Total Energy	-115.82304010 a.u.
RMS Gradient Norm	0.00002945 a.u.
Dipole Moment	0.2021 Debye
Point Group	CS
Job cpu time	0 days 0 hours 0 minutes 4.0 seconds

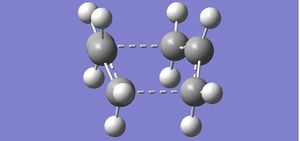
2 of the optimised structures were orientated to be 2.2A away from each terminal C to acquire the transition state.

Transition State Optimisation

The chair transition state was then optimised with Opt+ Freq:

Method

Method	Ground State	Hartree-Fock	Default Spin
Basis Set	3-21G
Charge	0	Spin	Singlet
Memory Limit	250 MB

File:CHAIRTSFREQ+OPT.LOG

Additionally we used the following options to carry out our calculation: Optimisation to a TS (Berny), calculate force constants once and additional keywords: Opt=NoEigen. The imaginary frequency of -818cm^-1, responsible for the wagging motion of the allyl groups in the transition state was clearly visible, showing the simultaneous formation and breakage of 2 C-C bonds.

Another option was to "freeze" each terminal C on the pair of molecules into place using the Redundant Coordinate Editor, selecting the bonds and choosing the "freeze coordinate" option. This was optimised with exactly the same method as above. Then the "frozen," optimised structure was "unfrozen" using the Redundant Coordinate Editor and choosing the "derivative" option for the same bonds that were frozen. This was optimised with exactly the same method as above, but the force constants were never calculated. With that method the imaginary vibration at 818cm^-1 was visible.

Method

	Distance Between Terminal C/ A
Not frozen at all	2.2A
Frozen then unfrozen	2.02A

The close proximity of the terminal C on the allyls shows that during the transition state, the 2 allyls come closer together as a bond is about to form. 2.02A is the distance at which the bonds can break/make, attributed to the overlap of the VDW radii. The distance of 2.02A is also the computed final distance between the terminal C for the non-frozen coordinate method. Even though we used 2 different methods, we they eventually brought us to the same conclusion. However the second method may be unable to be used when lots of bond breaking/forming interactions are present, due to the level of computational power required.

Boat Transition State

The Anti-2 conformation of 1,5-hexadiene was labelled thusly:

The molecule was analysed with Opt+Freq:

Method

Optimise To A	TS (QST2)
Method	Ground State	Hartree-Fock	Default Spin
Basis Set	3-21G
Charge	0	Spin	Singlet

The QST2 method allowed us to specify the product and the reactant. Although the submitted job goes to completion, we are given a chair conformation:

Therefore, we had to rotate the structures to better match a boat transition state because the Gaussian program would not be able to locate the energy minima as it does not take into account the potential of a rotation about the central bond.

A second attempt was made by altering:

• the C2-C3-C4-C5 dihedral angle to 0 degrees.
• the C2-C3-C4 AND C3-C4-C5 dihedral angle to 100 degrees.

After running the above method exactly again, we got a better structure.

Its imaginary frequency at -840cm^-1 is analogous to the on seen at -819cm^-1 for the chair conformation. This shows that the vibration of the TS in boat conformation is more energetic, as a higher value of wave number states that more energy is involved.

Conformation of 1,5-Hexadiene

To analyze the conformation of 1,5-hexadiene, the Intrinsic Reaction Coordinate method was carried out on both transition states.

Method

Follow IRC	Forward Only
Force Constants	Calculate Always	Compute Points N=50	Default Spin

The Follow IRC function was computed to "Forward Only" because the rearrangement's reaction coordinate is symmetrical.

Chair Transition State

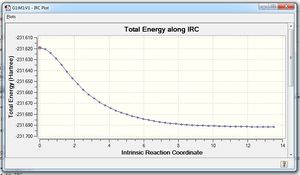
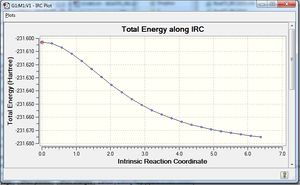
The calculations concluded with 44 intermediate geometries found, ending in a form very close to the gauche-4/gauche 2 structures in geometry and energy: -231.69157781 a.u

Follow-Up Methods to IRC

Method Used	Geometry	Energy/ a.u.
HF/321G Optimisation	Gauche-2	-231.69167
N=100	Gauche-4/Gauche-2	-231.69157781
Recalculating Force Constants at Each Step	Gauche-4/Gauche-2	-231.69157780

Optimisation with HF/3-21G basis sets yielded an increase of the overall energy into a Gauche-2 conformation, while increasing the number of steps taken did little to affirm the confirmation of the molecule to us, most likely because we had already reached an energy minima, as shown by the IRC path. Further corrections by recalculating the force constants at each step did not help either. Our calculations predict either a Gauche-2 or Gauche-4 structure being the preferred conformation from a chair transition state.

Boat Transition State

The calculations concluded with 23 intermediate geometries found: -231.67505708 a.u., which is not close to any of the anti/gauche conformations, but rather similar to the transition state, with the addition of a bond.

Follow-Up Methods to IRC

Method Used	Geometry	Energy/ a.u.
N=200	Gauche-3	-231.69262289
HF/3-21G Optimisation	Gauche-3	-231.69266121
Recalculating Force Constants at Each Step	Gauche-3	-231.69262289

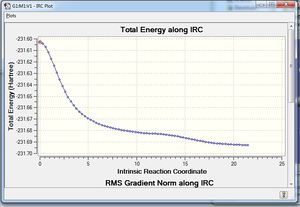
Our results for the initial N=50 method showed that we had not yet found an energy minima within the structure (as shown in the table below), therefore we increased the number of steps to 200, which yielded more promising results. By optimising with HF/3-21G, we arrived at a Gauche-3 conformation. Again, recalculating the force constants at each step did not seem to make a huge difference, mainly we because we had taken a lot of steps to reach an energy minima. Therefore the Gauche-3 conformation is predicted to be the preferred conformation from a boat transition state.

IRC Pathways

IRC n=50	IRC n=200

Optimisation of Boat and Chair Transition States to 6-31G

Both the chair and boat transition states were optimised to 6-31G and a frequency analysis was used.

Method

Method	Ground State	DFT	Default Spin	B3LYP
Basis Set	6-31G
Charge	0	Spin	Singlet
Memory Limit	250 MB

Tabulation of Results and Activation Energies

In order to calculate the activation energies of the pathways, we compared the boat and chair transition structures to the anti-2 conformation, the lowest energy conformation of 1,3-hexadiene.

Tabulation of Results

Evidently the transition states have very different energies, despite similar geometries. It would be computationally less demanding to reoptimise with B3LYP/6-31G AFTER having optimised initially with HF/3-21G.

Tabulation of Activation Energies

Compared to the experimental values of:

• Boat 44.7 ± 2.0 kcal/mol at 0K
• Chair 33.5 ± 0.5 kcal/mol at 0K

it is clear that using the B3LYP/6-31G basis set gives a much more accurate description of the energies involved. As was described before, the energies are lower because the non-bonding, core orbitals are better described by the larger 6-31G basis set. Overall, the Cope rearrangement of 1,3-hexadiene proceeds through a chair transition state as it has the lower energy pathway, as shown by the chair transition state's lower energy. This is in line with the literature sources .

Diels-Alder Reaction

In order to probe the results shown by Diels Alder reactions, we used Gaussian to model the reactants, products and transition states. Such a method has been used by Houk to show that we could predict the stereoselectivity of Diels-Alder products by computational analysis of transition states. We aimed to establish a deeper understanding of 3 concepts:

• Symmetry of the molecular orbitals of the reactants and transition states
• Geometry of the reaction and the comparison of theoretical reaction pathways and simulations.
• Regioselectivity of Diels-Alder reactions.

General Method for Calculations

The following general method was employed for calculating the transition states:

• The rough structures were optimised with the following method:

Method	Ground State	Semi-Empirical	Default Spin	AM1
Charge	0	Spin	Singlet

• The C-C unformed bonds were frozen by using freeze coordinate functions. This was optimised again with the same method.
• The C-C unformed bonds were "un-frozen" by selecting the derivative option. Then the Opt+Freq function was run. If that was successful, the same calculation was performed with this method:

Method	Ground State	DFT	B3LYP
Basis Set	6-31G (d)
Charge	0	Spin	Singlet

When calculating the energies of molecules (non-transition state), the same method was applied, but the freeze coordinate/derivative functions were not used.

Reaction of Cis-Butadiene and Ethylene

We chose to study the HOMO and LUMOs in our systems as these are the reacting orbitals. We were relatively successful in this regards as our calculations matched closely with literature values.

MOs of Cis-Butadiene and Ethylene and Diels-Alder Transition State

	Cis-Butadiene	Ethylene	Transition State
HOMO
Symmetry	Anti-Symmetric	Symmetric	Symmetrical
LUMO
Symmetry	Symmetric	Anti-Symmetric	Symmetrical

The single imaginary frequency which showed that we found our transition state (818cm^-1), demonstrates a concerted bond formation on the same face of the molecule, agreeing with the theory of pericyclic reactions. (If the animation on the right hand picture is not playing, please click to view it.) Gaussview shows it as being negative because it is at an energy maxima, where the second derivative of the energy surface is negative. The lowest positive "real" frequency is 167cm^-1. This is a symmetry breaking motion with respect to the C_s plane, suggesting that such motions lead to an increase in energy.

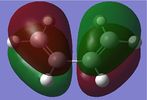
In the formation of the 2 C-C bonds, the LUMO of cis-butadiene and HOMO of ethylene are interacting, as we can see from the HOMO of the transition state, which is a shows an MO showing characteristics from both. This means that the reaction one of inverse electron demand. The cis-butadiene LUMO has 3 nodal planes, and ethylene HOMO has 2 nodal planes, one in the plane of the molecule and one perpendicular to that plane. The transition state has 3 nodal planes all of which are in the plane of the molecules. From the above table, we can see that the HOMO of the transition state is symmetrical. This MO, is the result of the combination of Cis-Butadiene's LUMO and Ethylene's HOMO, which are both symmetrical. Their corresponding symmetries allows the MOs to combine with each other, form bonds and hence react.

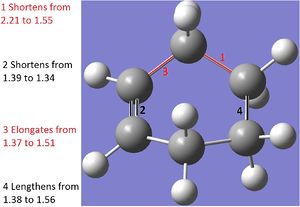
The above diagram shows a comparison between the Diels-Alder product and the transition state. Bond 1 is the newly formed C-C bond. In the transition state, the unformed C-C bond at 2.21A in close agreement with literature values of 2.21A. This is longer than normal C-C bonds: 1.54A for sp³ and 1.34A for sp², with the longest acyclic C-C bond ever reported being 1.67A. Therefore we can assume that the new bond is forming at those points as the VDW radii are overlapping (the VDW radius of each C is 1.7A). All of the bonds which turn from double to single bonds increase in bond length (bond 3, 4) as pi-electron density decreases, and vice versa (bond 2). Therefore, during the transition state, the bonds highlighted are mid-way into transforming into their product forms.

Reaction of Cyclohexa-1,3-diene and Maleic Anhydride

The reaction of cyclohexa-1,3-diene and maleic anhydride, can proceed via an endo or an exo transition state. Each of these gives a different isomeric product. In our attempt to understand the geometry and regioselectivity of the reaction, we probed the transition states and compared them to the products and reactants.

Imaginary Frequencies of Endo & Exo Transition States

	Endo Product	Exo Product
Products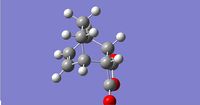
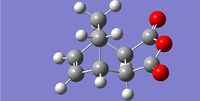
Imaginary Vibrations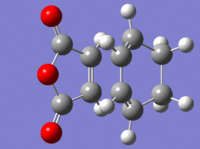
Frequencies/cm-1	-644	-647

Our negative figures show that we correctly found the transition states for our molecules. In further agreement with theory, we see that the vibration, which represents bond formation, is a concerted process. (Click on the Imaginary Vibration images to see the animation)

MOs of Endo & Exo Transition States

	Endo Transition State	Exo Transition State
Energies/a.u.	-605.61036818	-605.60359125
Geometries
HOMO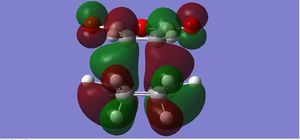
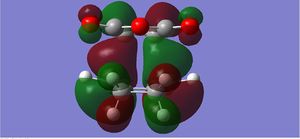
HOMO Sideways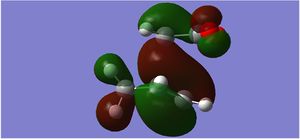
LUMO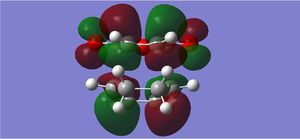
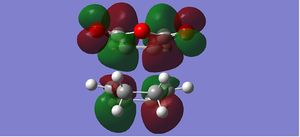
LUMO Sideways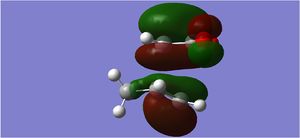

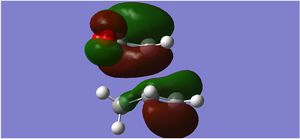
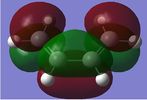
The endo form is more stabilised than the exo form as shown by the more negative energy (degree of stabilisation: -4.2526kcal/mol). This is in good correlation with current theory which states that the thermodynamic preference for the endo-product arises due to its stability. The LUMO of the transition states characteristically show a lack of orbital overlap, especially in the space between the molecules there are 2 distinctive nodal planes separating the 4 lobes, due to the different phases of the orbitals.

	Maleic Anhydride HOMO	Cyclohexadiene LUMO
MO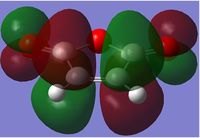
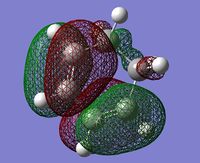
Symmetry	anti-symmetric	anti-symmetric

This is a classic Diels-Alder reaction whereby the product is formed as a result of the overlap of the LUMO of the dienophile, as shown by the HOMO of the transition state. The diene is particularly electron-poor due to the -(C=O)-O-(C=O)- fragment which is a strong electron withdrawing group. The

Bond Lengths of Endo & Exo Transition States

Endo Transition State	Exo Transition State
Distance between -(C=O)-O-(C=O)- and -CH=CH-: 2.85A	Distance between -CH2-CH2- fragmentand -(C=O)-O-(C=O)-: 2.43A

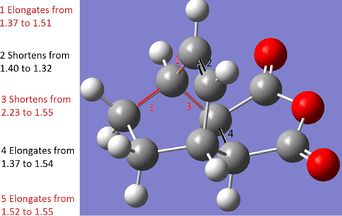
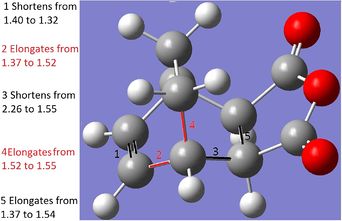
The above comparison of final products and transition state bond lengths shows the same pattern of results as the general Diels-Alder reaction: the lengthening of 2 double bonds into single bonds, the shortening of 1 single bond into a double bond and formation of 2 C-C bonds. Even in a larger molecular system, the "unformed" C-C bonds are still 2.26A and 2.23A apart, which are very similar distances shown in the ethylene/butadiene TS. Therefore we must assume that a distance of around 2.20A-2.26A for a VDW overlap to lead to bond formation.

From the geometries of the exo and endo transition states, the exo form is more sterically hindered because of the shorter distance between the -(C=O)-O-(C=O)- and the closest component of the diene, which is the H (2.43A). For the endo form, the distance between -(C=O)-O-(C=O)- and the closest component of the diene, the C is 2.85A. Both distances are close enough for a VDW overlap. Thus in both transition states, there are bonding and steric clashing interactions. The bonding interactions are very similar while the clashing is much stronger in exo, leading to a more strained product overall and increasing the energy of the transition state.

The Secondary Orbital Overlap Effect

MOs of Endo & Exo Transition States

	Endo Transition State	Exo Transition State
Energies/a.u.	-605.61036818	-605.60359125
HOMO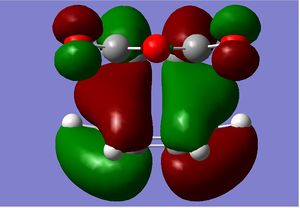
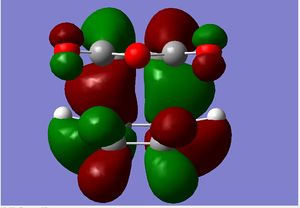
HOMO Sideways

The proposed reason for the thermodynamic stability of the endo-form arises due to the non-bonding overlap of the diene HOMO and the dienophile LUMO, as a result of frontier molecular orbital theory. This effect is said to stabilise the transition state, lowering the system's overall energy, thus being more thermodynamically favoured. However the kinetically favoured exo form is the major product, as the reaction is kinetically controlled. That is known as the Diels-Alder Endo rule.

However, from our calculations we can see that those secondary orbital interactions are not present. The secondary orbital interaction should be visible as the sp² orbitals of the diene interacting with the non-alkene, sp² carbons on the maleic anhydride. Instead all the sp² carbons' orbitals on the diene are interacting with the diene part of maleic anhydride. In fact there are nodal planes between the diene and the maleic anhydride in the TS as the orbitals are of different phases.

This leads us to assume that the driving force of endo-selectivity, from a thermodynamic view point, is not through secondary orbital stabilisations. Upon inspection of lower energy MOs of both transition states, we were not able to see any molecular orbitals which showed significant stabilisation through secondary orbital interactions in the endo TS. Further study in this area could be prompted by using better methods than B3LYP, as it does not factor in the effects of dispersion.

Conclusion

Through computational methods we were able to probe Diels-Alder reactions in greater detail than through spectroscopic methods in a laboratory setting. It allowed us to confirm that the bond forming and breaking were synchronous processes. The visulaisation of quantitatively calculated MOs, which would be near impossible without computational methods, aided our understanding of the electron demand in different Diels-Alder reactions. By calculating the different energies of the transition states, we were able to predict the major thermodynamic product of the reaction. We were surprised to find that secondary orbital interactions did not play a major part in the stabilisation of the endo transition state and this opens up a new area of study which deserves further attention.