Rep:Mod:dk2710
Optimisation of BH3
Altering Bond Lengths
The bond length of B-H units were altered to = 1.5A, from 1.18A.
The molecule on the left is the unaltered molecule, the molecule on the right has bond length at: 1.5A.
3-21G Basis Set
The BH3 molecule was optimised using the following methodology:
| Method | Ground State | DFT | Default Spin | B3LYP |
| Basis Set | 3-21G | |||
| Charge | 0 | Spin | Singlet |
File:BH3 OPTIMISATION 321G.LOG
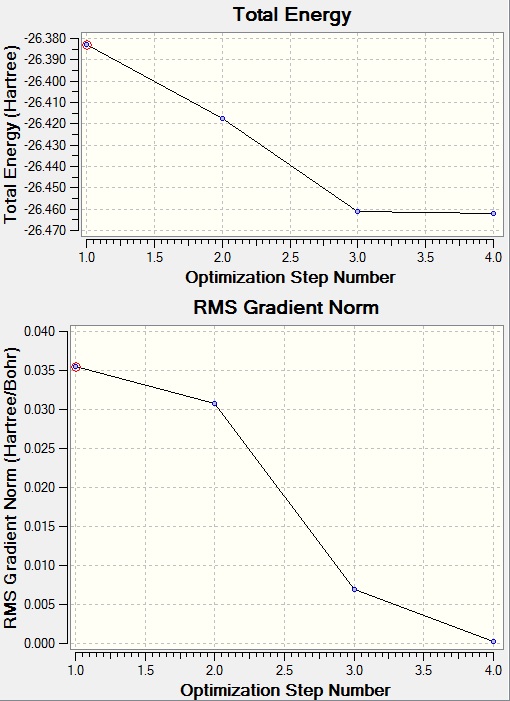
- B-H bond distance before optimisation: 1.50A
- B-H bond distance after optimisation: 1.19A
H-B-H angle is the same before and after optimisation: 120.0 degrees.
| File Name | BH3_OPTIMISATION_321G |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| Total Energy | -26.46226338 a.u. |
| RMS Gradient Norm | 0.0002067 a.u. |
| Dipole Moment | 0.0000 Debye |
| Point Group | D3H |
| Job cpu time | 0 days 0 hours 0 minutes 4.0 seconds |
Item Value Threshold Converged?
Maximum Force 0.000413 0.000450 YES
RMS Force 0.000271 0.000300 YES
Maximum Displacement 0.001610 0.001800 YES
RMS Displacement 0.001054 0.001200 YES
Predicted change in Energy=-1.071764D-06
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1935 -DE/DX = 0.0004 !
! R2 R(1,3) 1.1935 -DE/DX = 0.0004 !
! R3 R(1,4) 1.1935 -DE/DX = 0.0004 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
6-31G Basis Set
The BH3 molecule was further optimised by using a better basis set. It was run using the following methodology -
| Method | Ground State | DFT | Default Spin | B3LYP |
| Basis Set | 6-31G | d | p | |
| Charge | 0 | Spin | Singlet |
File:BH3 OPTIMISATION 631G.LOG
- B-H bond distance before optimisation: 1.19A
- B-H bond distance after optimisation: 1.192A
H-B-H angle is the same before and after optimisation: 120.0 degrees.
The further optimised bond length of 1.192A is a more accurate representation of the "real" B-H bonds. However, since BH3 exists as a dimer at gas phase, it is not possible to find the bond length of monomeric BH3. However, for diborane, a bond length of ~1.19A is quoted in literature. [1].
| File Name | BH3_optimisation_631G |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -26.615324 a.u. |
| RMS Gradient Norm | 0.000002 a.u. |
| Dipole Moment | 0.0000 Debye |
| Point Group | D3H |
| Job cpu time | 0 days 0 hours 0 minutes 3.0 seconds |
By using a 6-31G basis set, the energy of the molecule is reduced, as using a larger basis set describes the core (non bonding 1s on B) more accurately.
Item Value Threshold Converged?
Maximum Force 0.000009 0.000450 YES
RMS Force 0.000006 0.000300 YES
Maximum Displacement 0.000038 0.001800 YES
RMS Displacement 0.000025 0.001200 YES
Predicted change in Energy=-5.342736D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1923 -DE/DX = 0.0 !
! R2 R(1,3) 1.1923 -DE/DX = 0.0 !
! R3 R(1,4) 1.1923 -DE/DX = 0.0 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Optimisation of TlBr3
A molecule of TlBr3 was created on Gaussian with its symmetry restricted to DH3 and the tolerance set to: 0.0001(very tight). This was optimized using the following method.
| Method | Ground State | DFT | Default Spin | B3LYP |
| Basis Set | LanL2DZ | |||
| Charge | 0 | Spin | Singlet |
File:TlBr3 optimisation LANL2DZ.LOG
https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/
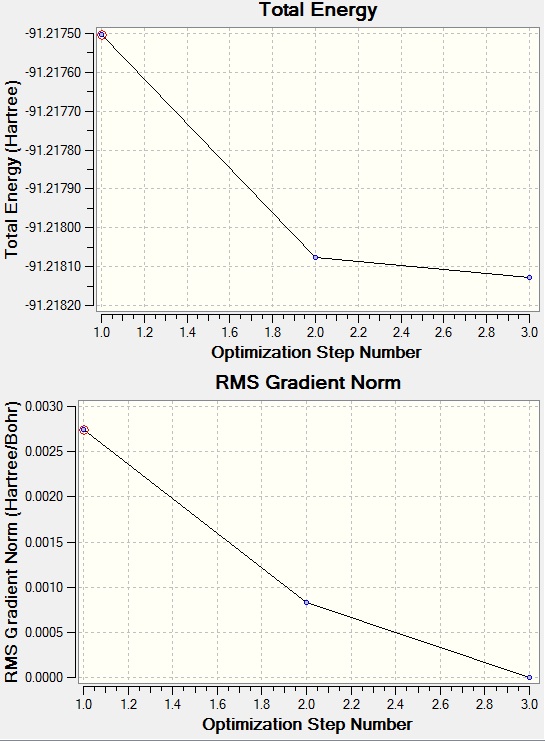
- Tl-Br bond distance before optimisation: 2.69A
- Tl-Br bond distance after optimisation: 2.65A
Br-Tl-Br angle is the same before and after optimisation: 120.0 degrees.
| File Name | TlBr_3_optimisation_LANL2DZ |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | LANL2DZ |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -91.2181285 a.u. |
| RMS Gradient Norm | 0.0000009 a.u. |
| Dipole Moment | 0.0000 Debye |
| Point Group | D3H |
| Job cpu time | 0 days 0 hours 0 minutes 9.0 seconds |
Item Value Threshold Converged?
Maximum Force 0.000002 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000022 0.001800 YES
RMS Displacement 0.000014 0.001200 YES
Predicted change in Energy=-6.084033D-11
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 2.651 -DE/DX = 0.0 !
! R2 R(1,3) 2.651 -DE/DX = 0.0 !
! R3 R(1,4) 2.651 -DE/DX = 0.0 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Comparison With Literature
We could not find a suitable comparison with literature. Only TlBr3 compounds with 4 coordinate Tl centres were found. Therefore we used a mercurial analogue to our molecule: the Hg(II)Br3 ion. According to J.G. White, the average bond length of Hg-Br was 2.5217A [2] The slightly shorter bond length of the Hg-Br is in line with expectations as the ionic radii of Hg is slightly smaller than Tl. Therefore, the 6-31G basis set is suitable to approximate the bond length.
Optimisation of BBr3
The BBr3 molecule was made by replacing Hydrogens on the 6-31G optimized BH3 molecule with terminal Br. This was then optimized using the following method.
| Method | Ground State | DFT | Default Spin | B3LYP |
| Basis Set | GEN | |||
| Charge | 0 | Spin | Singlet |
In the additional keywords section, "pseudo=read gfinput" was entered. The input file was edited to look like the below, before calculations on SCAN.
%chk=C:\Users\dk2710\Dropbox\Labs\3rdyearlab\Patricia Hunt\Proper\BBr3\temp\bbr3.chk # opt b3lyp/gen geom=connectivity gfinput pseudo=read BBr3 Optimisation 0 1 B 0.00000000 0.00000000 0.00000000 Br 1.74937131 -1.01000001 0.00000000 Br -1.74937131 -1.01000001 0.00000000 Br 0.00000000 2.02000000 0.00000000 1 2 1.0 3 1.0 4 1.0 2 3 4 B 0 6-31G(d,p) **** Br 0 LanL2DZ **** Br 0 LanL2DZ
https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/21609
- B-Br bond distance before optimisation: 2.00A
- B-Br bond distance after optimisation: 1.93A
Br-B-Br angle is the same before and after optimization: 120.0 degrees.
| File Name | log_65592 |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | Gen |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -64.4364530 a.u. |
| RMS Gradient Norm | 0.0000038 a.u. |
| Dipole Moment | 0.0000 Debye |
| Point Group | D3H |
| Job cpu time | 0 days 0 hours 0 minutes 18.1 seconds |
Item Value Threshold Converged?
Maximum Force 0.000008 0.000450 YES
RMS Force 0.000005 0.000300 YES
Maximum Displacement 0.000036 0.001800 YES
RMS Displacement 0.000023 0.001200 YES
Predicted change in Energy=-4.027374D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.934 -DE/DX = 0.0 !
! R2 R(1,3) 1.934 -DE/DX = 0.0 !
! R3 R(1,4) 1.934 -DE/DX = 0.0 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Comparison of BH3, TlBr3, BBr3
| BH3 | TlBr3 | BBr3 | |
| Bond Length | 1.19 | 2.65 | 1.93 |
The bond lengths are in order: TlBr3 > BBr3 > BH3.
TlBr3 > BBr3 because the atomic radii of Tl (170pm) > B (90pm).[1]. Thus a larger central atom results in a longer bond, given that the ligand is the same. Tl's S and P orbitals are bigger than the ones on B. Therefore a weaker overlap will be present for the Tl-Br bond than the B-Br bond. Tl and B are both bonding covalently in this case. BBr3 > BH3 because the atomic radii of Br (120pm) > H (53pm). [2] Thus a larger ligand results in a longer bond, given that the central atom is the same. Br and H both bond covalently, however Br has lone pairs which can be used to donate into the orthogonal p-orbital on the B. This would shorten the bond slightly, through better overlap, however Br is too large compared to H for the p-donation effect to show any relevance. Sometimes Gaussview doesn't draw the bonds where we expect because the software is primed to create bonds within a molecule if the distance between 2 atoms is sufficient for orbital interaction. A bond in Gaussian's context is the interaction of electrons between atoms. It is the interaction of filled bonding molecular orbitals between 2 or more atoms.
Frequency Analysis of BH3
Before we carry out an analysis of the vibrational modes of BH3, we must carry out a frequency analysis of BH3 to see whether our molecule was correctly optimised.
B-H bond distance before and after frequency analysis: 1.19A.
H-B-H is: 120.0 degrees.
| File Name | DONGWHIKIM_BH3_FREQ |
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G (d,p) |
| Charge | 0 |
| Spin | Singlet |
| Total Energy | -26.6153236 a.u. |
| RMS Gradient Norm | 0.0000024 a.u. |
| Dipole Moment | 0.0000 Debye |
| Point Group | D3H |
| Job cpu time | 0 days 0 hours 0 minutes 3.0 seconds |
Item Value Threshold Converged?
Maximum Force 0.000005 0.000450 YES
RMS Force 0.000002 0.000300 YES
Maximum Displacement 0.000019 0.001800 YES
RMS Displacement 0.000009 0.001200 YES
Predicted change in Energy=-1.323374D-10
Optimization completed.
-- Stationary point found.
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
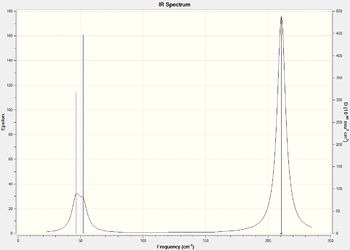
The following extract from the vibrational analysis shows that the molecule was optimized to an energy minimum. The top line of the "Low frequencies" values are within the ±15cm-1 meaning that the molecule was correctly optimized.
Low frequencies --- -0.9033 -0.7343 -0.0054 6.7375 12.2491 12.2824 Low frequencies --- 1163.0003 1213.1853 1213.1880
| Number | Form of Vibration | Frequency/cm-1 | Intensity | Symmetry Point Group |
| 1 |  Wagging (All H move in and out of plane, B moves in a similar manner but in the opposite direction) |
1160 | 93 | A2" |
| 2 |  Scissoring (2 H move symmetrically towards and away from each other) |
1210 | 14 | E' |
| 3 |  Rocking (2 H move asymmetrically and the last H moves at a symmetrically to 1 of the H, but with a greater range of motion ) |
1210 | 14 | E' |
| 4 |  Symmetric Stretching (All H move stretch symmetrically from B, which remains stationary) |
2580 | 0.0000 | A1' |
| 5 |  Asymmetric Stretching (2 H stretch away from/to the B centre asymmetrically, 3rd H is stationary) |
2720 | 126 | E' |
| 6 |  Asymmetric Stretching (2 H stretch away from/to the B centre symmetrically, 3rd H stretches away from/to the B centre, asymmetrically to the other 2 H) |
2720 | 127 | E' |
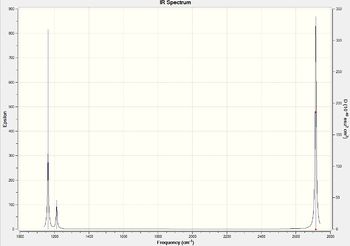
Though we have 6 modes of vibration, we see 3 peaks in the spectrum as only 5 modes are IR active and 2 of them are degenerate. Mode 4 is IR inactive as it doesn't induce a dipole moment. Modes 1 and 2 and 5 and 6 appear as the same peak as their symmetry labels are E' as they are degenerate.
Frequency Analysis of TlBr3
https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/21658
Tl-Br bond distance before and after vibrational analysis: 2.65095A Br-Tl-Br angle is the same before and after vibrational analysis: 120 degrees.
| File Name | DONGWHIKIM_TlBr3_FREQ |
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G (d,p) |
| Charge | 0 |
| Spin | Singlet |
| Total Energy | -26.6153236 a.u. |
| RMS Gradient Norm | 0.0000024 a.u. |
| Dipole Moment | 0.0000 Debye |
| Point Group | D3H |
| Job cpu time | 0 days 0 hours 0 minutes 3.0 seconds |
Item Value Threshold Converged?
Maximum Force 0.000005 0.000450 YES
RMS Force 0.000002 0.000300 YES
Maximum Displacement 0.000019 0.001800 YES
RMS Displacement 0.000009 0.001200 YES
Predicted change in Energy=-1.323374D-10
Optimization completed.
-- Stationary point found.
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Low frequencies --- -0.9033 -0.7343 -0.0054 6.7375 12.2491 12.2824 Low frequencies --- 1163.0003 1213.1853 1213.1880
| Number | Form of Vibration | Frequency/cm-1 | Intensity | Symmetry Point Group |
| 1 |  Scissoring (2 Br move symmetrically towards and away from each other) |
46 | 4 | E' |
| 2 |  Rocking (2 Br move asymmetrically towards and away from each other, 3rd Br moves similarly to one of them but with a greater range of motion) |
46 | 4 | E' |
| 3 |  Wagging(All Br move asymmetrically in and out of the plane, Tl moves in and out of the plane counter to the motion of the Brs) |
50 | 6 | A2" |
| 4 |  Symmetric Stretching (All Br move stretch symmetrically from Tl, which remains stationary) |
170 | 0.0000 | A1' |
| 5 |  Asymmetric Stretching (2 Br stretch away from/to the Tl centre asymmetrically, 3rd H is stationary) |
210 | 25 | E' |
| 6 |  Asymmetric Stretching (2 Br stretch away from/to the Tl centre symmetrically, 3rd Br stretches away from/to the B centre, asymmetrically to the other 2 Br) |
210 | 25 | E' |
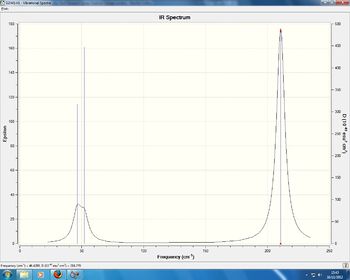
Again, we see 3 peaks in the spectrum as only 5 modes are IR active and 4 are degenerate. Modes 1, 2, 3, 5 and 6 are active because their movements lead to a dipole moment, which lead to a peak on the spectrum.
Vibrational Comparison of BH3 and TlBr3
By using different basis sets, the potential energy surface of the molecule will be higher/lower. Using a larger basis set (e.g. 6-31G) will characterise the core much more accurately (the 1s orbital on the central atom). If the potential energy surface are not the equivalent, then a fair comparison will not be possible. Using a different optimisation method will result in a different potential energy surface for the molecule and the energy minima will be inequivalent for 2 differently optimised molecules. The frequency analysis is taken so that we could be sure that the molecule was optimised to an energy minima.
| Symmetry Point Group | BH3 | TlBr3 |
| A"2 | |
|
| Frequency/cm-1 | 1160 | 50 |
| Intensity | 93 | 6 |
| E' | |
|
| Frequency/cm-1 | 1210 | 46 |
| Intensity | 14 | 4 |
| E' | |
|
| Frequency/cm-1 | 1210 | 46 |
| Intensity | 14 | 4 |
| A'1 | |
|
| Frequency/cm-1 | 2580 | 170 |
| Intensity | 0 | 0 |
| E' | |
|
| Frequency/cm-1 | 2720 | 210 |
| Intensity | 126 | 25 |
| E' | |
|
| Frequency/cm-1 | 2720 | 210 |
| Intensity | 126 | 25 |
As both molecules are trigonal planar (D3h) they have 6 modes of vibration. 3N-6 and 3(4)-6=6. All the modes of vibration are of the same symmetry in both molecules and accordingly the energies of the symmetries are the same, as shown by the same frequencies and intensities for each symmetry. Both molecules have only 3 peaks because 5 of the vibrations are IR active (induce a change in dipole moment). These are the vibrations of A"2, E' and A'1 symmetry. Generally, the vibrational modes show a greater range of motion for the BH3 molecule, than the thallium tribromide molecule since B-H bonds (1.19232A) are shorter and thus stronger than the Tl-Br bonds (2.65095A).
The frequencies and corresponding intensities of the same symmetry of vibrations are lower for the TlBr3 molecule than for the BH3, as the borane has shorter bonds since B and H are smaller than Tl and Br. Thus for the same vibration greater energy is required to get the same motion. The intensities are lower for TlBr3 as Tl and Br are both less electronegative and have more diffuse electron clouds than B and H. The relative placement of the peaks are very similar in the spectra. The A"2 and E' vibrations are close together and the A'1 and E' are close together while the 2 groups are far apart in vibrational energy. This is because the A"2 and E' modes are wagging and scissoring vibrations, while the A'1 and E' are stretches (asymmetric/symmetric) which are much more energetic as they involve a change in the electron density. An increase in the frequencies is observed as you increase the mode number. This is observed in both BH3 and TlBr3. The modes increase in enegry down the table. However for TlBr3 the A"2 and E' (rocking) were re-ordered, ie the A"2 vibration was mode 3 and the E' rocking was mode 1. This is because in the A"2 motion, the central atom moves whereas in the E' motion, the central atom does not. As the mass difference of Tl and Br (46au) is far greater than the mass difference of B and H, (4 au), the A"2 is more energetic than the the E' for TlBr.
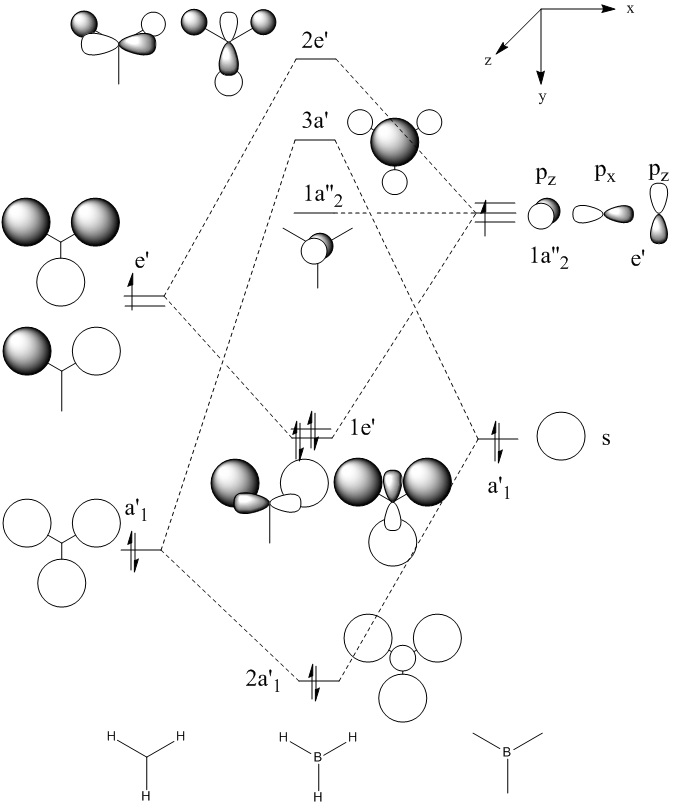
Molecular Orbitals of BH3
A calculation was run using 6-31G (p,d) optimized BH3, keywords pop=full was included and full NBO was included from the NBO tab.
File:BH3 OPTIMISATION 631GMO.LOG
| File Name | BH3_opt |
| File Type | .chk |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(D,P) |
| Charge | 0 |
| Spin | Singlet |
| Total Energy | -26.6153236 a.u. |
| RMS Gradient Norm | 0.0000024 a.u. |
| Dipole Moment | 0.0000 Debye |
| Point Group | D3H |
| Job cpu time | 0 days 0 hours 0 minutes 4.0 seconds |
Item Value Threshold Converged?
Maximum Force 0.000005 0.000450 YES
RMS Force 0.000003 0.000300 YES
Maximum Displacement 0.000019 0.001800 YES
RMS Displacement 0.000012 0.001200 YES
Predicted change in Energy=-1.333735D-10
Optimization completed.
-- Stationary point found.
Gaussian calculated the energy level of the 1s orbital for B as well. It's clear that it's an S orbital as it is very low in energy (-6.54kJ/mol) and because of its round shape.
Energy levels descend down the table in order of increasing energy level
| Orbital Number | LCAO | "Real" MO | Energy of "Real" MO/a.u. | Energy of "Real" MO/ kJ mol -1 |
| 1 |  |
 |
-0.57221 | -1500 |
| 2 |  |
 |
-0.42902 | -1130 |
| 3 |  |
 |
-0.42902 | -1130 |
| 4 |  |
 |
-0.19830 | -520 |
| 5 |  |
 |
+0.7745 | +2030 |
| 6 |  |
 |
+0.7745 | +2030 |
| 7 |  |
 |
+0.8819 | +2320 |
We can see that LCAO, though it is an qualitative analysis, is a surprisingly good rough match with the quantitative results from Gaussian. LCAO certainly doesn't account for the merging of electron densities which does not give it the smooth flowing shapes of the Gaussian pictures. Instead it gives us orbital overlaps. For the "real" MOs, we can see that proximity to same or different phases warps the shape of the atomic orbitals. In 6, the out of phase interaction of the p and s orbitals warps their respective shapes to shift density away from each other and resulting in a node between the out of phase orbitals. Whereas in 3, the opposite applies, where the atomic orbitals merge together as a result of their in-phase interactions. It is This shows that qualitative LCAO is sufficient for a first approximation for "visualising" molecular orbitals and also predicting the relative energy levels of simple molecules.
NH3 analysis
NH3 analysis
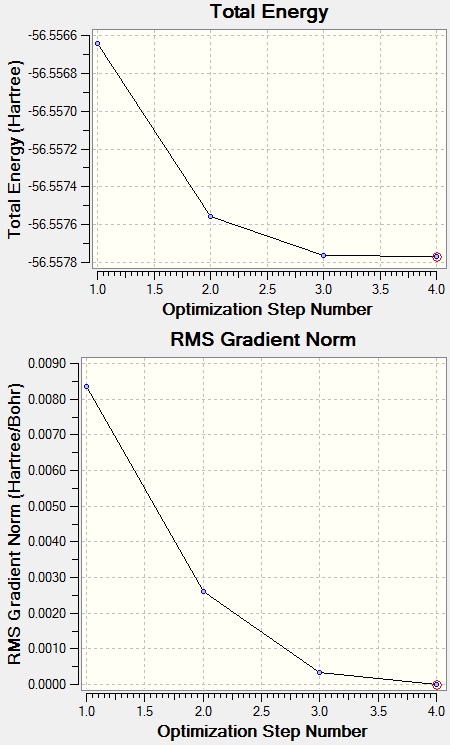
NH3 was opitimised with Opt+Freq the following method:
| Method | Ground State | DFT | Default Spin | B3LYP |
| Basis Set | 6-31G | d | p | |
| Charge | 0 | Spin | Singlet |
File:DongwhiKim NH3 ULTRAFINE.LOG
Bond length before optimisation: 1.00A
Bond length after optimisation: 1.02A
Bond angle before optimisation: 109.47
Bond angle after optimisation: 105.75
| File Name | DongwhiKim_NH3_ULTRAFINE |
| File Type | .chk |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G (d,p) |
| Charge | 0 |
| Spin | Singlet |
| Total Energy | -56.557769 a.u. |
| RMS Gradient Norm | 0.000003 a.u. |
| Dipole Moment | 1.85Debye |
| Point Group | C1 |
| Job cpu time | 0 days 0 hours 0 minutes 9.0 seconds |
Item Value Threshold Converged?
Maximum Force 0.000006 0.000015 YES
RMS Force 0.000004 0.000010 YES
Maximum Displacement 0.000014 0.000060 YES
RMS Displacement 0.000009 0.000040 YES
Predicted change in Energy=-1.141612D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7446 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7446 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7446 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8637 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
NH3 Vibrational analysis
Low frequencies --- -0.0129 -0.0023 -0.0017 7.1033 8.1047 8.1050 Low frequencies --- 1089.3834 1693.9368 1693.9368
| Number | Form of Vibration | Frequency/cm-1 | Intensity | Symmetry Point Group |
| 1 |  Wagging (All H move in and out of plane, N is stationary) |
1090 | 145 | A1 |
| 2 |  Rocking (2 H move asymmetrically and the last H moves at a symmetrically to 1 of the H, but with a greater range of motion ) |
1690 | 14 | E |
| 3 |  Modified scissoring (2 H move symmetrically, 3rd H moves at a perpendicular angle)
|
1690 | 14 | E |
| 4 |  Symmetric Stretching (All H move stretch symmetrically from N, which remains stationary) |
3460 | 1 | A1 |
| 5 |  Asymmetric Stretching (2 H stretch away from/to the N centre asymmetrically, 3rd H is stationary) |
3590 | 0.2699 | E |
| 6 |  Asymmetric Stretching (2 H stretch away from/to the N centre symmetrically, 3rd H stretches away from/to the B centre, asymmetrically to the other 2 H) |
3590 | 0.2699 | E |
Again, the stretching modes have higher frequencies as they are more energetic.
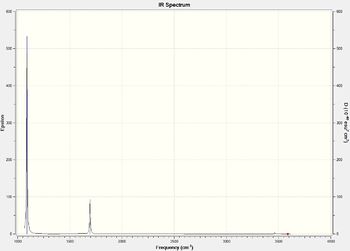
NH3 MO Analysis
File:DONGWHIKIM NH3 ULTRAFINEMO.LOG
The first orbital is the filled S orbital of the N (-10 kJ/Mol).
Energy levels descend down the table in order of increasing energy level.
| Orbital Number | MO | Energy of "Real" MO/ kJ mol 1 |
| 2 |  |
-2220 |
| 3 |  |
-1180 |
| 4 |  |
-1180 |
| 5 |  |
-670 |
| 6 |  |
+210 |
| 7 |  |
+440 |
| 8 |  |
+440 |
NH3 NBO Analysis
File:DONGWHIKIM NH3 ULTRAFINEMO.LOG
Charge limits were: -1.000 to +1.000.
Summary of Natural Population Analysis
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
N 1 -1.12514 1.99982 6.11104 0.01429 8.12514
H 2 0.37505 0.00000 0.62250 0.00246 0.62495
H 3 0.37505 0.00000 0.62250 0.00246 0.62495
H 4 0.37505 0.00000 0.62250 0.00246 0.62495
=======================================================================
* Total * 0.00000 1.99982 7.97852 0.02166 10.00000
The natural charge value 0 reflects the molecule's uncharged nature. The core value ~2 shows that there 2 electrons which are not bonding, (1s of N). The valence value ~8 reflects the 8 electrons in bonding MOs. The Total value of the Total value: 10, shows the 10 electrons in the entire system, including 1s of N. The numbers are not whole numbers because Gaussian views the molecule in terms of electron density which is modified by electronegativity (of which N>H), thus even though N has 6 valence electrons, the valence population is slightly larger than 6, as N is more electronegative and attracts the electron density in a covalent bond more closely to itself.
Bond Orbital/Coefficients/Hybrids
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.99909) BD ( 1) N 1 - H 2
( 68.83%) 0.8297* N 1 s( 24.86%)p 3.02( 75.05%)d 0.00( 0.09%)
0.0001 0.4986 0.0059 0.0000 0.0000
0.0000 0.8155 0.0277 -0.2910 0.0052
0.0000 0.0000 -0.0281 -0.0087 0.0013
( 31.17%) 0.5583* H 2 s( 99.91%)p 0.00( 0.09%)
0.9996 0.0000 0.0000 -0.0289 0.0072
2. (1.99909) BD ( 1) N 1 - H 3
( 68.83%) 0.8297* N 1 s( 24.86%)p 3.02( 75.05%)d 0.00( 0.09%)
0.0001 0.4986 0.0059 0.0000 -0.7062
-0.0239 -0.4077 -0.0138 -0.2910 0.0052
0.0076 0.0243 0.0140 0.0044 0.0013
( 31.17%) 0.5583* H 3 s( 99.91%)p 0.00( 0.09%)
0.9996 0.0000 0.0250 0.0145 0.0072
3. (1.99909) BD ( 1) N 1 - H 4
( 68.83%) 0.8297* N 1 s( 24.86%)p 3.02( 75.05%)d 0.00( 0.09%)
0.0001 0.4986 0.0059 0.0000 0.7062
0.0239 -0.4077 -0.0138 -0.2910 0.0052
-0.0076 -0.0243 0.0140 0.0044 0.0013
( 31.17%) 0.5583* H 4 s( 99.91%)p 0.00( 0.09%)
0.9996 0.0000 -0.0250 0.0145 0.0072
The data shows that there are 3 bonds, 1 lone pair and 1 non-bonding orbital. There are 3 N-H bonds, of which the N contributes ~69% of the electron density and the H contributes the rest. The coefficients of each individual atomic orbital show that the orbitals from N are sp3 hybridised as they get ~75% contribution from p and ~25% contribution from s. The coefficients for each bonding orbital show how much each atomic orbital from each atom contributes to the bond.
4. (1.99982) CR ( 1) N 1 s(100.00%)
1.0000 -0.0002 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000
This is the 1s on the N.
5. (1.99721) LP ( 1) N 1 s( 25.38%)p 2.94( 74.52%)d 0.00( 0.10%)
0.0001 0.5036 -0.0120 0.0000 0.0000
0.0000 0.0000 0.0000 0.8618 -0.0505
0.0000 0.0000 0.0000 0.0000 -0.0310
This shows that the lone pair on the N is also held in an sp3 hybridised orbital.
Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis
Threshold for printing: 0.50 kcal/mol
E(2) E(j)-E(i) F(i,j)
Donor NBO (i) Acceptor NBO (j) kcal/mol a.u. a.u.
===================================================================================================
within unit 1
5. LP ( 1) N 1 / 16. RY*( 1) H 2 1.01 1.43 0.034
5. LP ( 1) N 1 / 17. RY*( 2) H 2 0.67 2.17 0.034
5. LP ( 1) N 1 / 20. RY*( 1) H 3 1.01 1.43 0.034
5. LP ( 1) N 1 / 21. RY*( 2) H 3 0.67 2.17 0.034
5. LP ( 1) N 1 / 24. RY*( 1) H 4 1.01 1.43 0.034
5. LP ( 1) N 1 / 25. RY*( 2) H 4 0.67 2.17 0.034
As there is no value > 20kcal/mol, ther is no significant mixing of the orbitals.
Natural Bond Orbitals (Summary)
The following shows the energy level of the filled orbitals. As expected, the N-H bonds are the same in energy (-0.60417 au, -1586.25kJ/mol), the non-bonding 1s of N is the lowest in energy (-14.16768 au, 37197.24kJ/mol) and the lone pair is highest in energy (-0.31757 au, -833.78kJ/mol), which would explain why NH3's reactivity is greatly due in part to the lone pair.
Molecular unit 1 (H3N)
1. BD ( 1) N 1 - H 2 1.99909 -0.60417
2. BD ( 1) N 1 - H 3 1.99909 -0.60417
3. BD ( 1) N 1 - H 4 1.99909 -0.60417
4. CR ( 1) N 1 1.99982 -14.16768
5. LP ( 1) N 1 1.99721 -0.31757 16(v),20(v),24(v),17(v)
21(v),25(v)
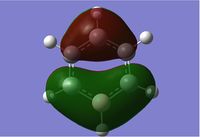
NH3BH3 Analysis
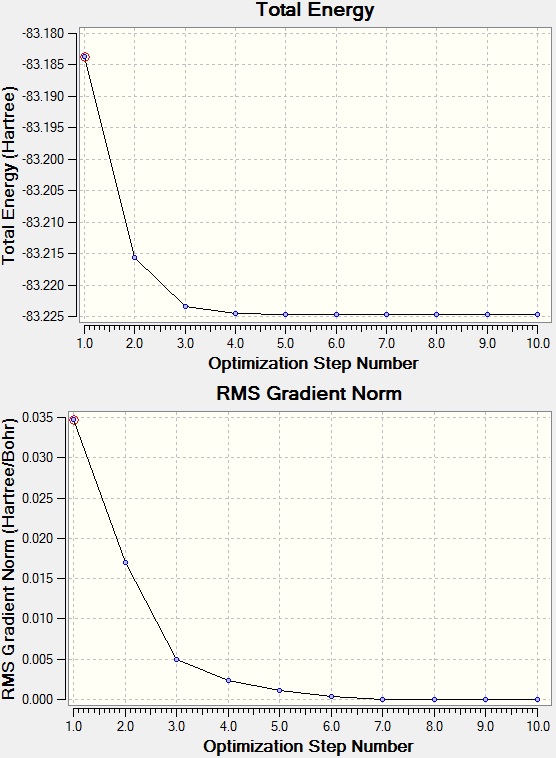
Optimisation and Frequency Analysis
| Method | Ground State | DFT | Default Spin | B3LYP |
| Basis Set | 6-31G | d | p | |
| Charge | 0 | Spin | Singlet |
File:DONGWHIKIM NH3BH3 OPT+FREQ.LOG
| File Name | DongwhiKim_NH3BH3_Opt+Freq |
| File Type | .chk |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G (d,p) |
| Charge | 0 |
| Spin | Singlet |
| Total Energy | -83.22468911 a.u. |
| RMS Gradient Norm | 0.00000131 a.u. |
| Dipole Moment | 5.56 Debye |
| Point Group | |
| Job cpu time | 0 days 0 hours 0 minutes 12.0 seconds |
Item Value Threshold Converged?
Maximum Force 0.000002 0.000015 YES
RMS Force 0.000001 0.000010 YES
Maximum Displacement 0.000029 0.000060 YES
RMS Displacement 0.000015 0.000040 YES
Predicted change in Energy=-1.254689D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,7) 1.0185 -DE/DX = 0.0 !
! R2 R(2,7) 1.0185 -DE/DX = 0.0 !
! R3 R(3,7) 1.0185 -DE/DX = 0.0 !
! R4 R(4,8) 1.2098 -DE/DX = 0.0 !
! R5 R(5,8) 1.2098 -DE/DX = 0.0 !
! R6 R(6,8) 1.2098 -DE/DX = 0.0 !
! R7 R(7,8) 1.6677 -DE/DX = 0.0 !
! A1 A(1,7,2) 107.8748 -DE/DX = 0.0 !
! A2 A(1,7,3) 107.8748 -DE/DX = 0.0 !
! A3 A(1,7,8) 111.0241 -DE/DX = 0.0 !
! A4 A(2,7,3) 107.8748 -DE/DX = 0.0 !
! A5 A(2,7,8) 111.024 -DE/DX = 0.0 !
! A6 A(3,7,8) 111.0239 -DE/DX = 0.0 !
! A7 A(4,8,5) 113.874 -DE/DX = 0.0 !
! A8 A(4,8,6) 113.8739 -DE/DX = 0.0 !
! A9 A(4,8,7) 104.5972 -DE/DX = 0.0 !
! A10 A(5,8,6) 113.874 -DE/DX = 0.0 !
! A11 A(5,8,7) 104.5973 -DE/DX = 0.0 !
! A12 A(6,8,7) 104.5973 -DE/DX = 0.0 !
! D1 D(1,7,8,4) -180.0006 -DE/DX = 0.0 !
! D2 D(1,7,8,5) -60.0006 -DE/DX = 0.0 !
! D3 D(1,7,8,6) 59.9995 -DE/DX = 0.0 !
! D4 D(2,7,8,4) -60.0005 -DE/DX = 0.0 !
! D5 D(2,7,8,5) 59.9995 -DE/DX = 0.0 !
! D6 D(2,7,8,6) -180.0004 -DE/DX = 0.0 !
! D7 D(3,7,8,4) 59.9994 -DE/DX = 0.0 !
! D8 D(3,7,8,5) -180.0006 -DE/DX = 0.0 !
! D9 D(3,7,8,6) -60.0005 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Low frequencies --- -4.0188 -0.0003 -0.0001 0.0015 1.2321 3.9060 Low frequencies --- 263.3726 632.9622 638.4319
Comparison of Energies of NH3, BH3, NH3BH3
| Species | Bond Energy/ au | Bond Energy/kJ mol-1 |
| NH3 | -56.5577687 | 148490 |
| BH3 | -26.6153236 | 69880 |
| NH3BH3 | -83.2246891 | -218510 |
Thus the predicted value for NH3BH3 is: -83.1730924 a.u. (-218370 kJ mol-1) The calculated value for NH3BH3 is -83.22468911 a.u.(-218510 kJ mol-1) and therefore the difference is: 0.05159675 a.u (140 kJ mol-1), which is the bond enthalpy of The literature value of 122.55 kJ mol-1 for the bond enthalpy of B-N, from Leroy et. al [3] shows that our guess was quite good. The literature source had calculated the value from a least squares method via the MULFRA program. Perhaps next time a more suitable basis set could be used. A better basis set would give us a view closer to reality as it would lower the energy of the potential energy surface by characterising the core orbitals more accurately. This was why the literature value has a lower value than our calculated value.
Errors in Calculations
In our calculations, the errors for energy were around ± ~10kJ mol-1 or 3.8088 x 10-3 a.u. For dipoles the error margins were: ±0.01Debye For frequencies: ±10cm-1 For angles: ±0.1 degrees For bond distances: 0.01A Intensities were rounded to whole numbers.
Aromaticity
The concept of aromaticity is covered qualitatively in our lecture course through a MO theory based on LCAO but a quantitative view has never been comprehensively understood. Therefore we decided to carry out an analysis of the charge distribution on benzene and its analogues, compare some of the MOs of the analogues to benzene and visualise the MO diagram of benzene with the LCAO visualisation method.
Benzene
Optimisation and Frequency Analysis
Benzene was opitimised with Opt+Freq the following method:
| Method | Ground State | DFT | Default Spin | B3LYP |
| Basis Set | 6-31G | d | p | |
| Charge | 0 | Spin | Singlet |
Keyword used: integral=grid=ultrafine.
File:DongwhiKim BenzeneFreq+Opt.log
| File Name | DongwhiKim_BenzeneFreq+Opt |
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G (d,p) |
| Charge | 0 |
| Spin | Singlet |
| Total Energy | -232.25820415 a.u. |
| RMS Gradient Norm | 0.00000849 a.u. |
| Dipole Moment | 0.00Debye |
| Point Group | C1 |
| Job cpu time | 0 days 0 hours 10 minutes 9.0 seconds |
Proof of convergence:
Item Value Threshold Converged?
Maximum Force 0.000013 0.000015 YES
RMS Force 0.000004 0.000010 YES
Maximum Displacement 0.000052 0.000060 YES
RMS Displacement 0.000017 0.000040 YES
Predicted change in Energy=-1.961204D-09
Optimization completed.
-- Stationary point found.
Frequency analysis data:
Low frequencies --- -4.7117 -0.0005 0.0002 0.0004 5.2722 6.2063 Low frequencies --- 414.5308 414.5721 621.0881
MO Analysis
The energy levels were found out by running an Energy calculation with NBO set to "full NBO" and with the keywords "pop=full" https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/21878
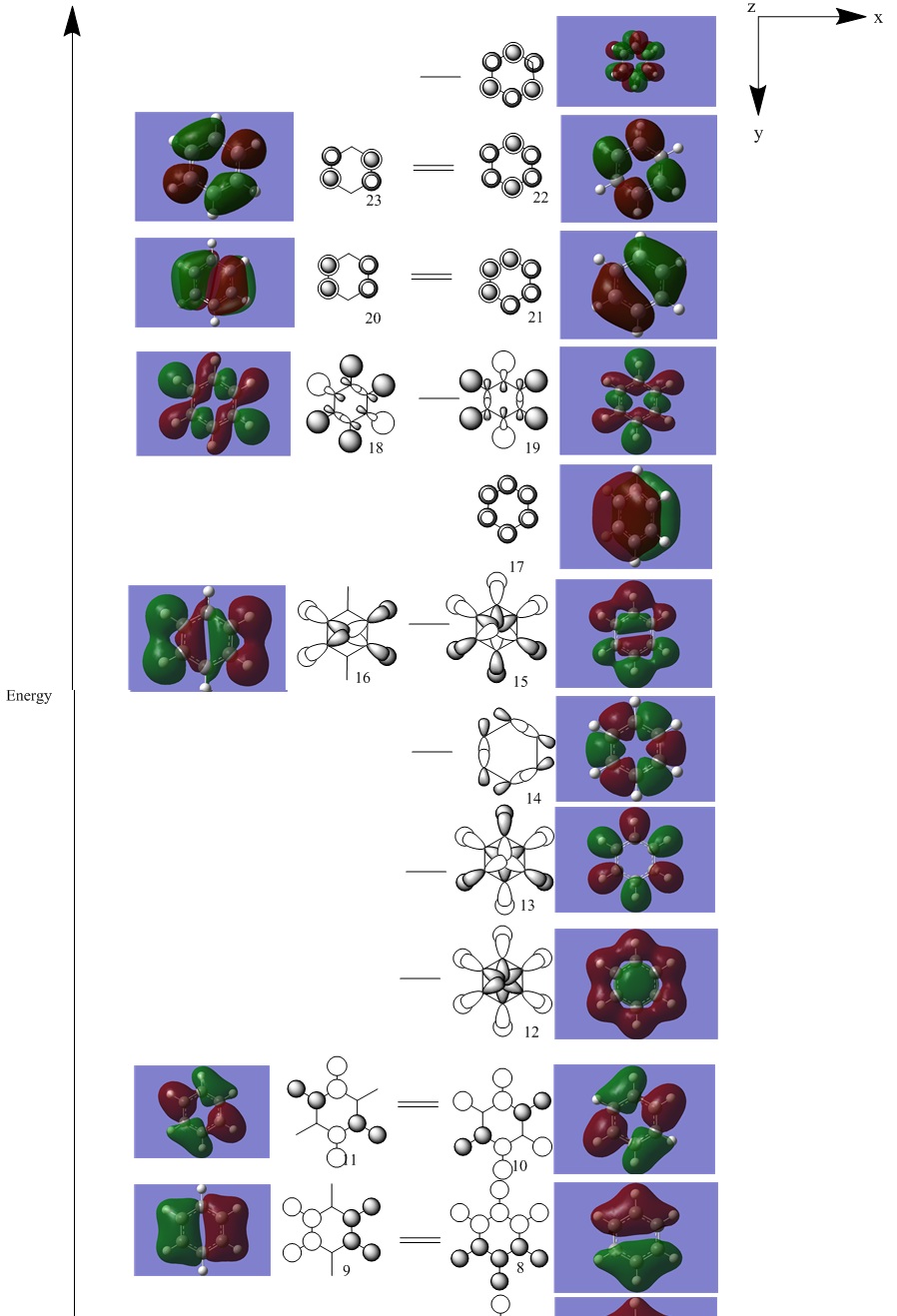
The pi-system is made up of MO: 17, 20-23 and 27. 22 and upwards are anti-bonding orbitals in the pi-system. The pi-system shows the aromaticity of benzene as they are formed by the overlap of co-planar p-orbitals. The occupancy of only the bonding pi-MOs and their delocalisation shows that the pi electron density is spread throughout the entire carbon chain. The Huckel theory states that the reactivity of benzene molecules are dominated by the pi-system and that the pi and sigma systems can be dealt separately. As the HOMO are the pi-MOs, this is the reason why the Huckel approximation is valid. The rest of the system are the sigma orbitals which are interleved between the pi-system.
Boratabenzene
Optimisation and Frequency Analysis
Boratabenzene was opitimised with Opt+Freq the following method:
| Method | Ground State | DFT | Default Spin | B3LYP |
| Basis Set | 6-31G | d | p | |
| Charge | 0 | Spin | Singlet |
Keyword used: integral=grid=ultrafine.
File:DongwhiKim BoratabenzeneFreq+Opt.log
| File Name | DongwhiKim_BoratabenzeneFreq+Opt |
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G (d,p) |
| Charge | -1 |
| Spin | Singlet |
| Total Energy | -219.02052299 a.u. |
| RMS Gradient Norm | 0.00000532 a.u. |
| Dipole Moment | 2.85 Debye |
| Point Group | C1 |
| Job cpu time | 0 days 0 hours 10 minutes 34.9 seconds |
Proof of convergence:
Item Value Threshold Converged?
Maximum Force 0.000006 0.000015 YES
RMS Force 0.000003 0.000010 YES
Maximum Displacement 0.000044 0.000060 YES
RMS Displacement 0.000016 0.000040 YES
Predicted change in Energy=-1.002817D-09
Optimization completed.
-- Stationary point found.
Frequency analysis data:
Low frequencies --- -7.1813 -0.0004 0.0002 0.0002 3.7588 4.3237 Low frequencies --- 371.2985 404.4152 565.0737
MO Analysis
The energy levels were found out by running an Energy calculation with NBO set to "full NBO" and with the keywords "pop=full" https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/21880
Pyridinium
Optimisation and Frequency Analysis
Pyridinium was opitimised with Opt+Freq the following method:
| Method | Ground State | DFT | Default Spin | B3LYP |
| Basis Set | 6-31G | d | p | |
| Charge | 0 | Spin | Singlet |
Keyword used: integral=grid=ultrafine.
File:DongwhiKim PyrdiniumFreq+Opt.log
| File Name | DongwhiKim_PyrdiniumFreq+Opt |
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G (d,p) |
| Charge | +1 |
| Spin | Singlet |
| Total Energy | -248.66806092 a.u. |
| RMS Gradient Norm | 0.00000124 a.u. |
| Dipole Moment | 1.87 Debye |
| Point Group | C1 |
| Job cpu time | 0 days 0 hours 10 minutes 45.4 seconds |
Proof of convergence:
Item Value Threshold Converged?
Maximum Force 0.000003 0.000015 YES
RMS Force 0.000001 0.000010 YES
Maximum Displacement 0.000020 0.000060 YES
RMS Displacement 0.000006 0.000040 YES
Predicted change in Energy=-6.782434D-11
Optimization completed.
-- Stationary point found.
Frequency analysis data:
Low frequencies --- -9.4678 -3.2446 -0.7134 -0.0009 -0.0008 0.0005 Low frequencies --- 391.9004 404.3357 620.1999
MO Analysis
The energy levels were found out by running an Energy calculation with NBO set to "full NBO" and with the keywords "pop=full" DOI: 10042/21879 https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/21879
Borazine
Optimisation and Frequency Analysis
Borazine was opitimised with Opt+Freq the following method:
| Method | Ground State | DFT | Default Spin | B3LYP |
| Basis Set | 6-31G | d | p | |
| Charge | 0 | Spin | Singlet |
Keyword used: integral=grid=ultrafine.
File:DongwhiKim BorzaineFreq+Opt.log
| File Name | DongwhiKim_BorzaineFreq+Opt |
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G (d,p) |
| Charge | 0 |
| Spin | Singlet |
| Total Energy | -242.68459859 a.u. |
| RMS Gradient Norm | 0.00000358 a.u. |
| Dipole Moment | 0.00 Debye |
| Point Group | C1 |
| Job cpu time | 0 days 0 hours 10 minutes 36.3 seconds |
Proof of convergence:
Item Value Threshold Converged?
Maximum Force 0.000008 0.000015 YES
RMS Force 0.000002 0.000010 YES
Maximum Displacement 0.000058 0.000060 YES
RMS Displacement 0.000022 0.000040 YES
Predicted change in Energy=-1.057972D-09
Optimization completed.
-- Stationary point found.
Frequency analysis data:
Low frequencies --- -8.3090 -4.6145 -0.0007 0.0003 0.0009 5.2367 Low frequencies --- 289.5659 289.6387 404.4359
MO Analysis
The energy levels were found out by running an Energy calculation with NBO set to "full NBO" and with the keywords "pop=full" https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/21878
NBO Analysis of Benzene, Boratabenzene, Pyridinium and Borazine
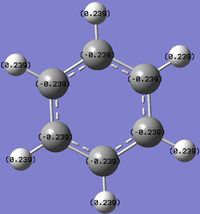
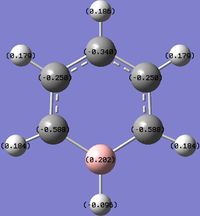
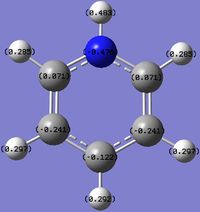
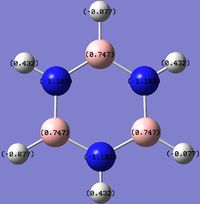
An NBO analysis of benzene and its analogues was carried out to visualise the distribution and balancing of charge among the molecules.
| Benzene | Boratabenzene | Pyridinium | Borazine | |
| Charge Distribution |  |
 |
 |
|
| Limits | -0.239 to +0.239 | -0.588 to +0.588 | -0.483 to +0.483 | -1.102 to +1.102 |
| Charge Distribution in Numbers |  |
 |
 |
|
For benzene, there is a uniform distribution of charge around the molecule. However for the analogues, the relative electronegativities influence the charge on the atoms. Being bonded to a more electronegative atom will render it more positive as the more electronegative atom will attract the electrons in the covalent bond more strongly. This can be used to explain the following effects:
- C on C-H being more positive than H.
- B on B-H being more positive than H.
- B on C-B (boratabenzene) being more positive than C.
- H on N-H (pyridinium) being more positive than H on C-H (pyridinium).
And other similar ones.
It is clear that the negative charge on boratabenzene is delocalised over the C ortho to the Boron, as the charge of the rest of the molecule, except from the B and H (B-H) have similar to values in benzene but the ortho C are far more negative (vs. benzene). The positive charge is spread amongst the H, as shown by their less positive charge. For pyridinium the positive charge is delocalised mainly over the ortho carbons, especially on the H on N-H and to a lesser extent the Hydrogens, as the C are positive and the H are slightly more positive compared to benzene. The high positive charge on the H in N-H is due to N's greater electronegativity. Interestingly, on the negative boratabenzene, the ortho C changed charge by 0.349 (vs. benzene) and on the positive pyridinium the ortho C changed charge by 0.3018. In the case of borazine, charge is highly localised on each B, N and H. The differences in charges arise due to the same reasons described above, as N is more electronegative than B.
Interestingly for benzene, the analysis of the level of occupancy shows interesting characteristics about Gaussian's view of benzene. Benzene:
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.98098) BD ( 1) C 1 - C 2
( 50.00%) 0.7071* C 1 s( 35.20%)p 1.84( 64.76%)d 0.00( 0.04%)
-0.0001 0.5932 -0.0079 0.0006 0.6632
-0.0035 0.4545 0.0355 0.0000 0.0000
0.0145 0.0000 0.0000 0.0081 -0.0109
( 50.00%) 0.7071* C 2 s( 35.20%)p 1.84( 64.76%)d 0.00( 0.04%)
-0.0001 0.5932 -0.0079 0.0006 -0.6856
-0.0310 -0.4200 0.0177 0.0000 0.0000
0.0157 0.0000 0.0000 0.0053 -0.0109
2. (1.98098) BD ( 1) C 1 - C 6
( 50.00%) 0.7071* C 1 s( 35.20%)p 1.84( 64.76%)d 0.00( 0.04%)
-0.0001 0.5932 -0.0079 0.0006 0.0209
-0.0309 -0.8037 -0.0180 0.0000 0.0000
-0.0032 0.0000 0.0000 -0.0163 -0.0109
( 50.00%) 0.7071* C 6 s( 35.20%)p 1.84( 64.76%)d 0.00( 0.04%)
-0.0001 0.5932 -0.0079 0.0006 -0.0620
-0.0325 0.8015 0.0147 0.0000 0.0000
-0.0002 0.0000 0.0000 -0.0166 -0.0109
3. (1.66518) BD ( 2) C 1 - C 6
( 50.00%) 0.7071* C 1 s( 0.00%)p 1.00( 99.96%)d 0.00( 0.04%)
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.9997 -0.0133
0.0000 0.0107 -0.0163 0.0000 0.0000
( 50.00%) 0.7071* C 6 s( 0.00%)p 1.00( 99.96%)d 0.00( 0.04%)
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.9997 -0.0133
0.0000 0.0090 0.0173 0.0000 0.0000
4. (1.98306) BD ( 1) C 1 - H 7
( 62.04%) 0.7876* C 1 s( 29.57%)p 2.38( 70.39%)d 0.00( 0.04%)
0.0003 -0.5436 -0.0126 0.0010 0.7471
-0.0130 -0.3814 0.0066 0.0000 0.0000
0.0135 0.0000 0.0000 -0.0098 0.0105
( 37.96%) 0.6161* H 7 s( 99.95%)p 0.00( 0.05%)
-0.9997 -0.0014 -0.0203 0.0104 0.0000
5. (1.98098) BD ( 1) C 2 - C 3
( 50.00%) 0.7071* C 2 s( 35.20%)p 1.84( 64.76%)d 0.00( 0.04%)
-0.0001 0.5932 -0.0079 0.0006 0.7252
0.0290 -0.3471 0.0208 0.0000 0.0000
-0.0143 0.0000 0.0000 0.0085 -0.0109
( 50.00%) 0.7071* C 3 s( 35.20%)p 1.84( 64.76%)d 0.00( 0.04%)
-0.0001 0.5932 -0.0079 0.0006 -0.7065
-0.0001 0.3837 0.0357 0.0000 0.0000
-0.0125 0.0000 0.0000 0.0109 -0.0109
6. (1.66519) BD ( 2) C 2 - C 3
( 50.00%) 0.7071* C 2 s( 0.00%)p 1.00( 99.96%)d 0.00( 0.04%)
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.9997 -0.0133
0.0000 0.0105 -0.0164 0.0000 0.0000
( 50.00%) 0.7071* C 3 s( 0.00%)p 1.00( 99.96%)d 0.00( 0.04%)
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.9997 -0.0133
0.0000 -0.0195 -0.0012 0.0000 0.0000
7. (1.98306) BD ( 1) C 2 - H 8
( 62.04%) 0.7877* C 2 s( 29.57%)p 2.38( 70.39%)d 0.00( 0.04%)
-0.0003 0.5437 0.0126 -0.0010 -0.0433
0.0008 0.8377 -0.0146 0.0000 0.0000
-0.0017 0.0000 0.0000 -0.0166 -0.0105
( 37.96%) 0.6161* H 8 s( 99.95%)p 0.00( 0.05%)
0.9997 0.0014 0.0012 -0.0227 0.0000
8. (1.98098) BD ( 1) C 3 - C 4
( 50.00%) 0.7071* C 3 s( 35.20%)p 1.84( 64.76%)d 0.00( 0.04%)
0.0001 -0.5932 0.0079 -0.0006 -0.0620
-0.0325 0.8016 0.0147 0.0000 0.0000
0.0002 0.0000 0.0000 0.0166 0.0109
( 50.00%) 0.7071* C 4 s( 35.20%)p 1.84( 64.76%)d 0.00( 0.04%)
0.0001 -0.5932 0.0079 -0.0006 0.0209
-0.0309 -0.8037 -0.0180 0.0000 0.0000
0.0032 0.0000 0.0000 0.0163 0.0109
9. (1.98306) BD ( 1) C 3 - H 9
( 62.04%) 0.7877* C 3 s( 29.57%)p 2.38( 70.39%)d 0.00( 0.04%)
-0.0003 0.5437 0.0126 -0.0010 0.7039
-0.0123 0.4563 -0.0080 0.0000 0.0000
0.0152 0.0000 0.0000 0.0068 -0.0105
( 37.96%) 0.6161* H 9 s( 99.95%)p 0.00( 0.05%)
0.9997 0.0014 -0.0191 -0.0124 0.0000
10. (1.98098) BD ( 1) C 4 - C 5
( 50.00%) 0.7071* C 4 s( 35.20%)p 1.84( 64.76%)d 0.00( 0.04%)
-0.0001 0.5933 -0.0079 0.0006 -0.6631
0.0035 -0.4545 -0.0355 0.0000 0.0000
0.0145 0.0000 0.0000 0.0081 -0.0109
( 50.00%) 0.7071* C 5 s( 35.20%)p 1.84( 64.76%)d 0.00( 0.04%)
-0.0001 0.5932 -0.0079 0.0006 0.6856
0.0310 0.4199 -0.0177 0.0000 0.0000
0.0157 0.0000 0.0000 0.0053 -0.0109
11. (1.66518) BD ( 2) C 4 - C 5
( 50.00%) 0.7071* C 4 s( 0.00%)p 1.00( 99.96%)d 0.00( 0.04%)
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.9997 -0.0133
0.0000 -0.0195 -0.0008 0.0000 0.0000
( 50.00%) 0.7071* C 5 s( 0.00%)p 1.00( 99.96%)d 0.00( 0.04%)
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.9997 -0.0133
0.0000 0.0087 0.0174 0.0000 0.0000
12. (1.98306) BD ( 1) C 4 - H 10
( 62.04%) 0.7876* C 4 s( 29.57%)p 2.38( 70.39%)d 0.00( 0.04%)
-0.0003 0.5436 0.0126 -0.0010 0.7472
-0.0130 -0.3814 0.0066 0.0000 0.0000
-0.0135 0.0000 0.0000 0.0098 -0.0105
( 37.96%) 0.6161* H 10 s( 99.95%)p 0.00( 0.05%)
0.9997 0.0014 -0.0203 0.0104 0.0000
13. (1.98098) BD ( 1) C 5 - C 6
( 50.00%) 0.7071* C 5 s( 35.20%)p 1.84( 64.76%)d 0.00( 0.04%)
-0.0001 0.5932 -0.0079 0.0006 -0.7252
-0.0290 0.3471 -0.0208 0.0000 0.0000
-0.0143 0.0000 0.0000 0.0085 -0.0109
( 50.00%) 0.7071* C 6 s( 35.20%)p 1.84( 64.76%)d 0.00( 0.04%)
-0.0001 0.5932 -0.0079 0.0006 0.7065
0.0001 -0.3837 -0.0357 0.0000 0.0000
-0.0125 0.0000 0.0000 0.0109 -0.0109
14. (1.98306) BD ( 1) C 5 - H 11
( 62.04%) 0.7877* C 5 s( 29.57%)p 2.38( 70.39%)d 0.00( 0.04%)
0.0003 -0.5437 -0.0126 0.0010 -0.0433
0.0008 0.8377 -0.0146 0.0000 0.0000
0.0017 0.0000 0.0000 0.0166 0.0105
( 37.96%) 0.6161* H 11 s( 99.95%)p 0.00( 0.05%)
-0.9997 -0.0014 0.0012 -0.0227 0.0000
15. (1.98306) BD ( 1) C 6 - H 12
( 62.04%) 0.7877* C 6 s( 29.57%)p 2.38( 70.39%)d 0.00( 0.04%)
0.0003 -0.5437 -0.0126 0.0010 0.7039
-0.0123 0.4564 -0.0080 0.0000 0.0000
-0.0152 0.0000 0.0000 -0.0068 0.0105
( 37.96%) 0.6161* H 12 s( 99.95%)p 0.00( 0.05%)
-0.9997 -0.0014 -0.0191 -0.0124 0.0000
This shows that all the C-H bonds are sp2 hybridised, as shown by the ~30% contribution from s and ~70% contribution from p orbital. 6 of the C-C bonds are sp2, 3 of the C-C bonds are purely p overlaps. This shows that the figures from the analysis represent a snapshot of the bonding picture within benzene as we know through visualisation of the MOs that benzene has a delocalised pi-bond made up of p-orbital overlaps.
NBO Analysis of Benzene, Boratabenzene, Pyridinium and Borazine
| Benzene | Boratabenzene | Pyridinium | Borazine | |
| MO 8 |  |
 |
 |
|
| LCAO |  |
 |
|
|
| Energy/a.u. | -0.74000 | -0.46083 | -1.02631 | -0.83517 |
| Energy/kJ mol-1 | -1940 | -1210 | -2690 | -2190 |
| MO 12 |  |
 |
 |
|
| LCAO |  |
|
 |
|
| Energy/a.u. | -0.51686 | -0.28948 | -0.79009 | -0.55137 |
| Energy/kJ mol-1 | -1360 | -760 | -2070 | -1450 |
| MO 21 |  |
 |
 |
|
| Energy/a.u. | -0.24690 | -0.01095 | -0.50847 | -0.27593 |
| Energy/kJ mol-1 | -650 | -30 | -1330 | -720 |
| LCAO |  |
 |
|
|
For MO 8, all of the MOs are sigma overlaps which are bonding orbitals. They are formed from the overlap of s-orbitals. All show a nodal region. Benzene has a nodal plane across the molecule while the analogues have a nodal region bisecting the uppermost non-carbon atom. The nodal region splits the analogue molecules asymmetrically because the boratabenzene and pyridinium each have 5 fewer cv symmetry planes than benzene and borazine has 3 fewer cv symmetrical planes than benzene. The 2 lobes on pyridinium and boratabenzene are of roughly similar sizes. However, the lobe centering B is far larger than the lobe centering N.
For MO12, all of the MOs are sigma overlaps, formed by the overlap of s and p orbitals. There is also slight pi-overlap as shown by the ring-like phase around the central phase, as shown in benzene. In boratabenzene the "outer ring" of overlap isn't completely circular (or donut-like), as is the case with benzene. This is because because the boratabenzene has 5 fewer cv mirror planes compared to benzene. The MO on pyridinium is very similar to that of benzene, however there is no contribution from the p orbital of the para H. The borazine MO is the most distinctive out of the analogues, due to the very small contribution of the p orbitals from B. The common feature seems to be the overlap of the p orbitals within the centre of the rings for benzene and its analogues.
For MO 12, all of the MOs are pi overlaps which are bonding orbitals. This is a bonding orbital very similar to that of MO 8. However the overlaps are all of pi-symmetry and it's formed by p orbital overlap. Even the shapes of the lobes are very similar to MO 8.
Stabilisation of molecular orbitals(from most to least stabilised): pyridinium, borazine, benzene, boratabenzene. This order reflects the stabilisation of individual molecular orbitals due to the electronegativity of different substituents. By replacing C with a more electronegative substituent N (pyridinium), the MOs were lowered in energy. The opposite was true for replacing C with B. Out of the analogues, borazine matched the benzene's MOs' level of stabilisation because they are both neutral, borazine has only 3 fewer cv symmetries than benzene. The equal number of B and N in borazine allowed the even distribution of charge around the molecule.
Due to the loss of symmetry, pyridinium and boratabenzene have also lost degeneracy in their MOs. Out of the valence orbitals, boratabenzene has only 1 pair of degenerate MOs and pyridinium has 3 pairs of degenerate orbitals.
Conclusion
By modelling 4 different aromatic systems, we were able to compare their charge distributions, molecular orbitals and quantitatively visualise their aromaticity, whereas before with an LCAO based version of MO theory, we were able to develop only a qualitative picture. By using a quantitative method (Gaussian), we were able to see that the pi-MOs which affords a molecule its aromaticity is in fact interleved between a sigma-bonding framework of the rest of the ring molecule. From our first steps we can easily envisage investigating larger more complex aromatic systems with multiple charges.
Notes and References
- ↑ H. Heather, "The Boron Elements: Boron, Aluminum, Gallium, Indium, Thallium", Rosen Publishing Group., 2009
- ↑ F.A. Cotton, "Advanced Inorganic Chemistry", Wiley., 1988
- ↑ G. Leroy, M. Sana, C. Wilante , "Evaluation of Bond Energy Terms for the Various Types of Boron-Nitrogen Bonds", Theor Chim Acta, 1983, 85, 1555