Rep:Mod:dk2016
Introduction to molecular modelling 2
NH3 molecule:
Part 1:
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy (E(RB3LYP)): -56.55776873 a.u.
RMS Gradient: 0.00000323
Point group: C3V
Optimised H-N-H Bond angle: 105.745o
Optimised N-H Bond length: 1.01798Å
Item Value Threshold Converged?
Maximum Force 0.000006 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000014 0.001800 YES
RMS Displacement 0.000009 0.001200 YES
Predicted change in Energy=-1.141655D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7446 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7446 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7446 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8637 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
NH3 |
The optimisation file is linked to here
Part 2:
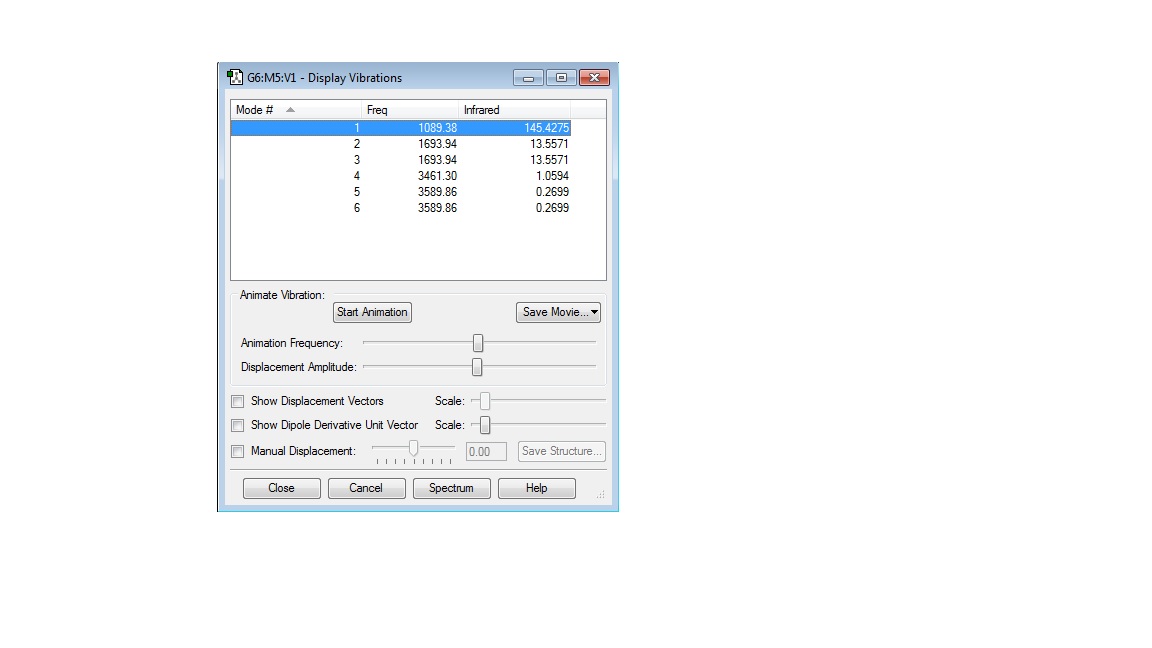
How many modes do you expect from the 3N-6 rule? 6
Which modes are degenerate (ie have the same energy)? 2 & 3 are degenerate as they have the same frequency of vibration (1693.94Hz). The same applies to 5 & 6, they are degenerate because they have the same frequency of vibration (3589.86Hz).
Which modes are "bending" vibrations and which are "bond stretch" vibrations? 1,2 & 3 are bending vibrations. 4,5 & 6 are bond stretch vibrations.
Which mode is highly symmetric? 4
One mode is known as the "umbrella" mode, which one is this? 1
How many bands would you expect to see in an experimental spectrum of gaseous ammonia? 4
In the NH3 molecule, I would expect the Nitrogen atom to have a negative charge due to the presence of the lone pair on the atom. However, the Hydrogen atoms would have a slight positive charge because the Nitrogen atom is more electronegative than the Hydrogen atoms, thus the electron density is withdrawn from the Hydrogen atom.
Nitrogen atom charge: -1.125e
Hydrogen atom charge: 0.375e
Part 3:
N2 molecule
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy (E(RB3LYP)): -109.52412868 a.u.
RMS Gradient: 0.00000060
Point group: D*H
Optimised N-N Bond angle: 180o
Optimised N-N Bond length: 1.10550Å
This measured bond length for the N2 molecule seems to be accurate with a literature value of 1.0975±0.0001. This data is from the following website: http://www.wiredchemist.com/chemistry/data/molecular-parameters
There is one mode of vibration for the N2 molecule, it oscillates at a frequency of 2457.33Hz
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.401001D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
N2 |
H2 molecule
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy (E(RB3LYP)): -1.17853936 a.u.
RMS Gradient: 0.00000017
Point group: D*H
Optimised H-H Bond angle: 180o
Optimised H-H Bond length: 0.74279Å
There is one mode of vibration for the H2 molecule, it oscillates at a frequency of 4465.68Hz
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
H2 |
E(NH3)= -56.55776873 a.u.
2*E(NH3)= -113.11553746 a.u.
E(N2)= -109.52412868 a.u.
E(H2)= -1.17853936 a.u.
3*E(H2)= -3.53561808 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -113.11553746 - (-109.52412868 + -3.53561808) = -0.0557907 a.u.
ΔE= -146.47849401 kJ/mol
Gaussian has used theoretical analysis rather than experimental results to determine the enthalpy change for this reaction. This means that through the use of mathematics we are making an estimation, we have a molecule of NH3, N2 and H2 in a vacuum and then we have calculated the energy of these molecules. As a result of the method used to determine the enthalpy of formation for NH3, the experimental value is different to that which I collected. The literature value of -92.4kJmol-1 is quite different and this is due to the reasons I have explained above. The literature value has been collected using experimental method and so is more reliable and accurate than mine achieved through computational analysis. This figure was obtained from: http://www.ausetute.com.au/haberpro.html
The product ammonia is more stable than the reactants as the enthalpy change of formation is negative, meaning more energy is released by the formation of the new bonds in the NH3 molecule than is required to break the bonds in the N2 and H2 molecules.
Parts 4 & 5:
H2 molecule
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy (E(RB3LYP)): -291.88802760 a.u.
RMS Gradient: 0.00000002
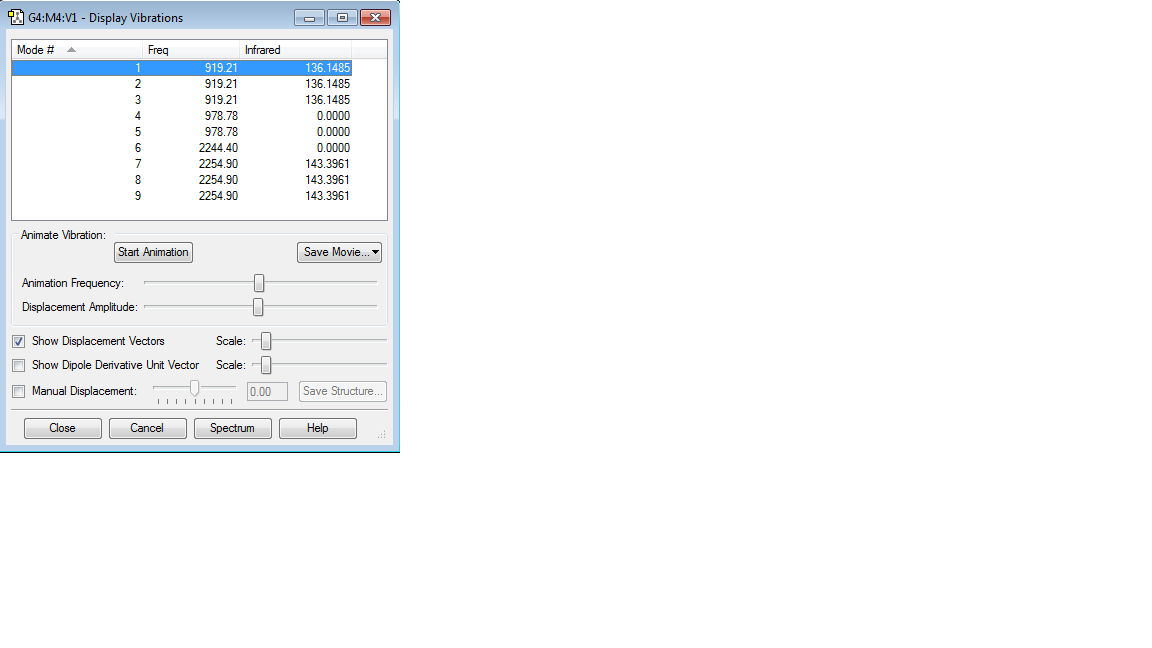
Point group: TD
Optimised H-Si-H Bond angle: 109.471o
Optimised Si-H Bond length: 1.48485Å
Charge on the Si atom: 0.336e
Charge on the H atom: -0.084e
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-2.452335D-14
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.4849 -DE/DX = 0.0 !
! R2 R(1,3) 1.4849 -DE/DX = 0.0 !
! R3 R(1,4) 1.4849 -DE/DX = 0.0 !
! R4 R(1,5) 1.4849 -DE/DX = 0.0 !
! A1 A(2,1,3) 109.4712 -DE/DX = 0.0 !
! A2 A(2,1,4) 109.4712 -DE/DX = 0.0 !
! A3 A(2,1,5) 109.4712 -DE/DX = 0.0 !
! A4 A(3,1,4) 109.4712 -DE/DX = 0.0 !
! A5 A(3,1,5) 109.4712 -DE/DX = 0.0 !
! A6 A(4,1,5) 109.4712 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -120.0 -DE/DX = 0.0 !
! D2 D(2,1,5,3) 120.0 -DE/DX = 0.0 !
! D3 D(2,1,5,4) -120.0 -DE/DX = 0.0 !
! D4 D(3,1,5,4) 120.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
SiH4 |
The optimisation file is linked to here
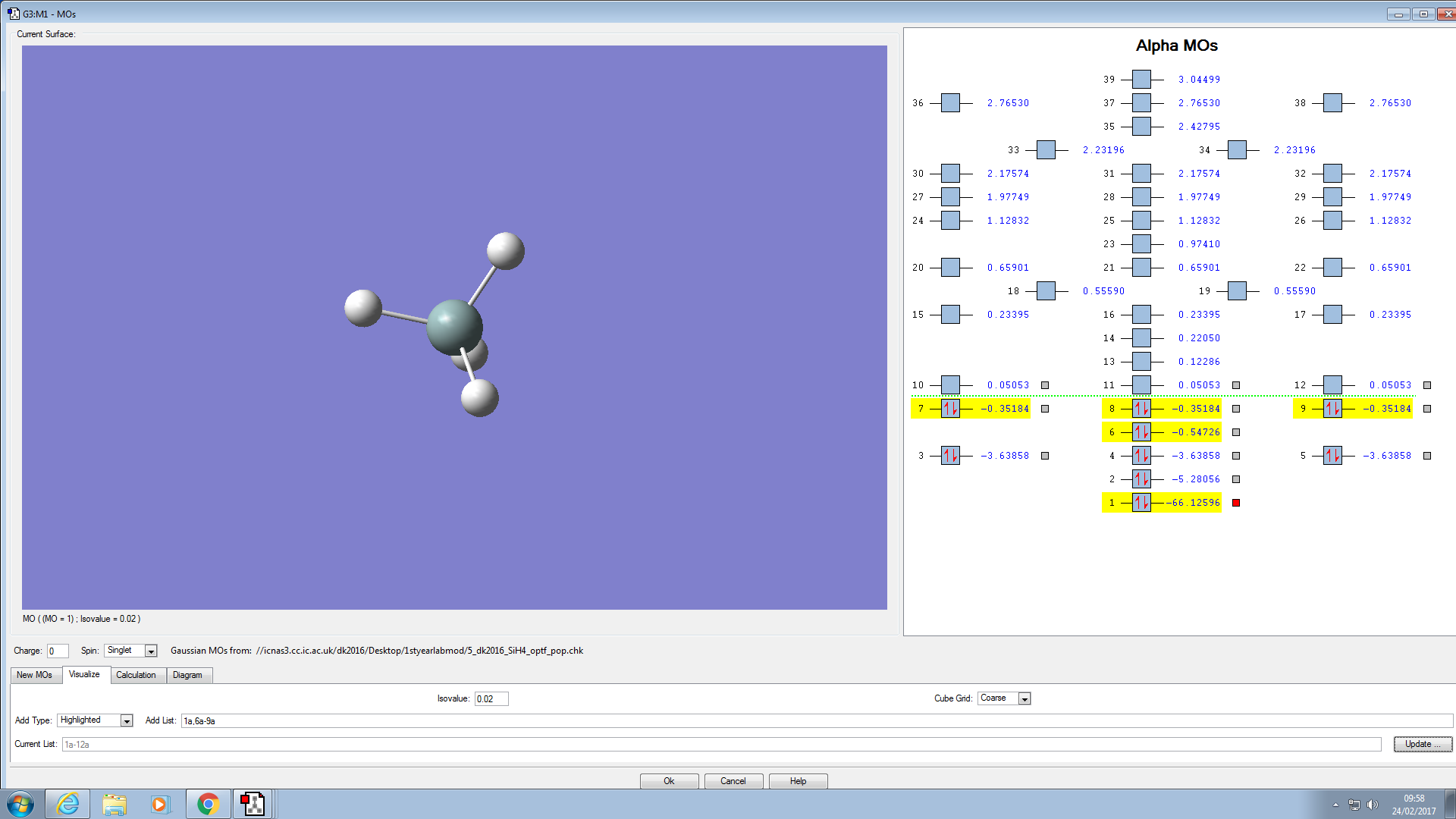
MOs in SiH4:
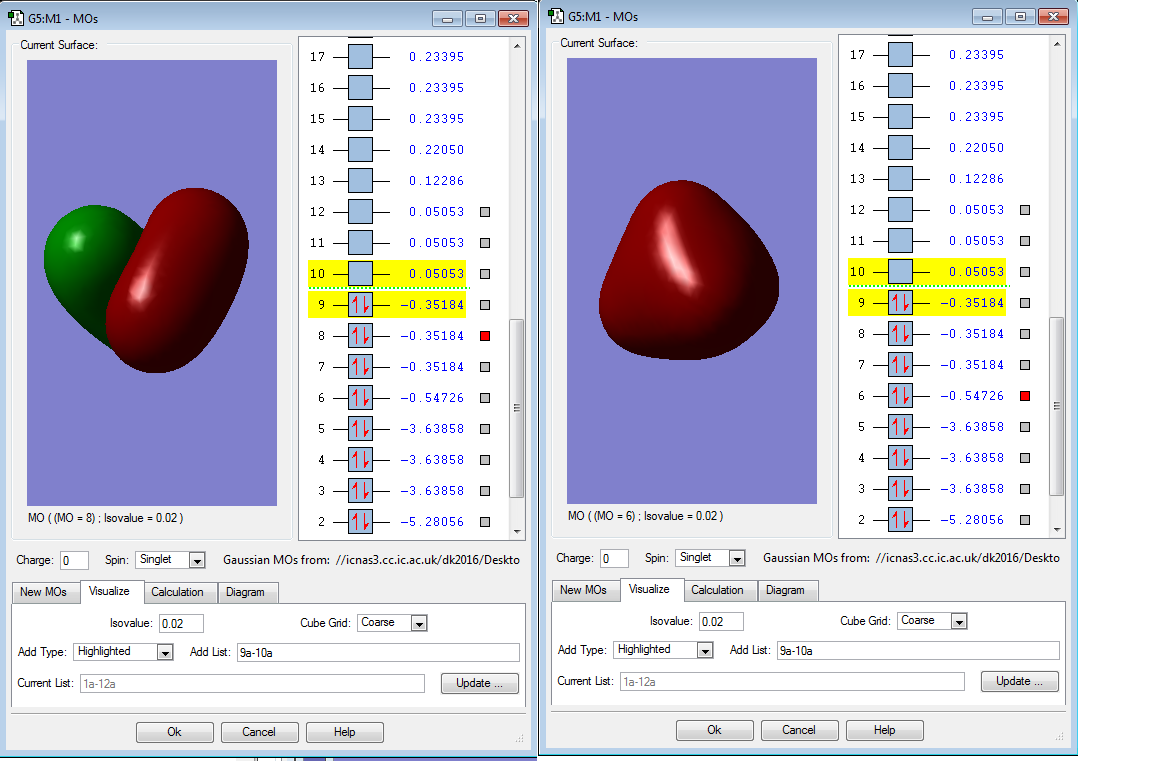
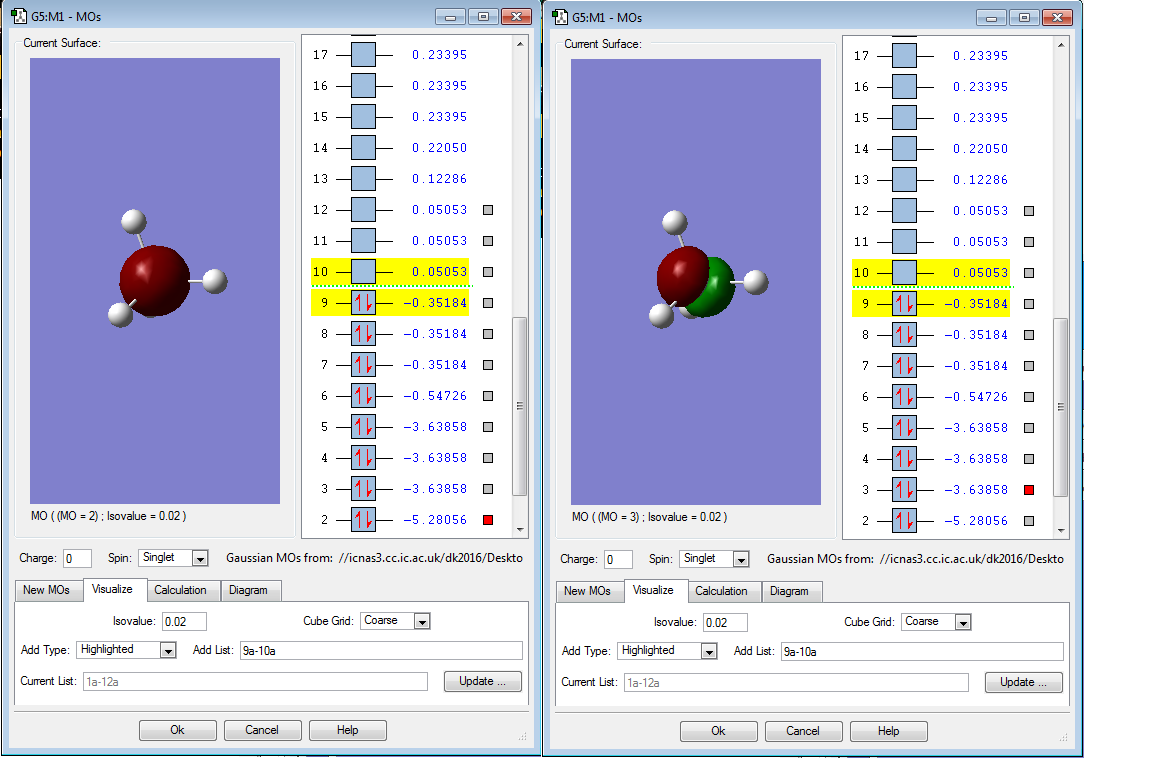
Below are the molecular orbitals I found for SiH4:
Molecular orbital 8 is the HOMO, this is because it is occupied and is the MO closest in energy to the LUMO. However, it is degenerate with MO 7 and 9, so they are both HOMOs also. Molecular orbital 6 is occupied but is too deep in energy to interact with the LUMO. MO 6 is a bonding orbital that is composed of the 4 Hydrogen 1s orbitals. The tetrahedral shape of the orbital mirrors the positions of the Hydrogen atoms around the central Si atom.
Molecular orbital 8 is also a bonding orbital, composed of 2 Hydrogen 1s orbitals and a Silicon p orbital.
Molecular orbital 10 is the LUMO, this is because it is unoccupied and is the lowest energy unoccupied orbital available (0.05053 a.u.). It is a bonding orbital
Molecular orbitals 2 and 3 are deep in energy (-5.28056 a.u. and -3.63858 a.u. respectively). They are too deep in energy to be considered for the HOMO. Also, as they are both occupied with a pair of electrons they cannot be LUMOs. Molecular orbitals 3,4 and 5 are degenerate with different orientations in space. Molecular orbital 2 is a large spherical shape and is a non-bonding orbital like MO 1. The Atomic orbital that contributes to this MO is 2s. For MO 3, the Atomic orbital that contributes to this Molecular orbital is 2p, this is proven by there being 3 degenerate Molecular orbitals.
Molecular orbital 1 is non-bonding and very deep in energy and is hidden inside the atom in this diagram. As it is so deep in energy (-66.12596 a.u.) indicating it is a Si 1s orbital. The character of this orbital is shown by the very low energy, 1s orbitals are very penetrating and are very close to the nucleus so experience a high electrostatic force of attraction. Thus, the orbital is very deep in energy.