Rep:Mod:dior101
Transition States and Reactivity
This module will utilise various computational methods using Gaussian, in order to predict the product outcome by studying the reaction coordinate pathways. This will be aided by a close examination of the possible transition state structures and their respective energies, vibrational frequencies, molecular orbitals and geometric parameters.
The Cope Rearrangement
The Cope rearrangement of 1,5-hexadiene was developed by Arthur C. Cope; it is a [3,3]-sigamtropic rearrangement, but its mechanistic reaction route has previously been ambiguous. By examining the reaction’s potential energy surface (PES), this exercise illustrates why it is now widely accepted that the rearrangement occurs via a concerted transition state. This is achieved by identifying the lowest energy minima and transition structures from the PES, employing computed calculations within Gaussian. The transition states identified in this reaction will either adopt a chair or boat conformation, which will be examined using methods such as Hartree-Fock (HF) and density functional theory (DFT).
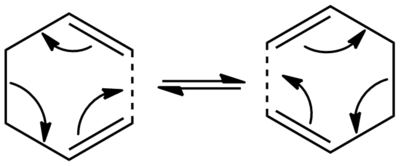
Optimising the Reactant and Product
Initially, rough anti-periplanar (180 o linkages across the central four central carbons) and gauche (60 o linkage) conformers of 1,5-hexadiene were drawn into Gaussview, which were both then tidied up using the clean function. The two structures were optimised using the Hartree-Fock method, with a 3-21G basis set that employs a Gaussian distribution to define the radial distribution functions. Once optimised, the conformers were identified by their point groups and labelled according to Appendix 1.
| Conformer | Optimised Structure | Energy (/Hartrees) | Appendix 1 Energies (/Hartrees) | Energy (kcal mol-1) | Point group | ||
| anti2 | -231.69254 | -231.69254 | -1.45 x 105 | Ci | |||
| Gauche3 | -231.69266 | -231.69266 | -1.45 x 105 | C1 |
The results from the table above show that the gauche conformer is in fact more stable than the anti structure by 1.2 x 10-4 Hartrees. Assumingly, anti2 would be the more sterically preferred conformer, but gauche3 shows favourable orbital overlap conferring overall stability to the conformer. This is evident by the orientation of the C=C π-orbital, which donates electron density to the adjacent C-H σ* orbital.
The 1,5-hexadiene structures drawn and optimised thus far have corresponded to two of the lowest energy conformers of the molecule, but there is another anti-periplanar conformer which is lower in energy than ‘’anti2’’. This was drawn in Gaussview and optimised using the HF method and 3-21G basis set. The resulting lowest energy anti conformer was then compared against the reference conformer, anti1, and the results are shown in the table below.
| Conformer | Optimised Structure | Energy (/Hartrees) | Appendix 1 Energies (/Hartrees) | Energy (kcal mol-1) | Point group | ||
| anti1 | -231.69260 | -231.69260 | -1.45 x 105 | C2 |
The slightly lower energy of anti1 compared to anti2 is rather insignificant; however, the extra stability of anti1 is conferred by the orthogonal orientation of one of the C=C bonds, which relieves some steric hindrance within the structure.
To illustrate how imperative different methods and basis sets make to the optimisation calculations and the final geometry of the structure, anti2 will be subjected to a higher level optimisation. This is achieved employing the DFT B3LYP method, with a 6-31G* basis set.
| Parameter | ||
|---|---|---|
| Energy (/Hartrees) | -231.69253528 | -234.61171040 |
| Energy (/kcalmol-1) | 1.45 x 105 | 1.47 x 105 |
| Bond length (C1=C2) | 1.31615 | 1.33350 |
| Bond length (C2-C3) | 1.50888 | 1.504025 |
| Bond length (C3-C4 central) | 1.55292 | 1.54806 |
| Bond length (C4-C5) | 1.50889 | 1.50425 |
| Bond length (C5=C6) | 1.31614 | 1.33351 |
| Dihedral angle (C1=C2-C3-C4) | -114.62091 | -118.61043 |
| Dihedral angle (C2-C3-C4-C5) | 179.96099 | -180.00000 |
| Dihedral angle (C3-C4-C5=C6) | 114.67825 | 118.61057 |
The DFT/B3LYP/6-31G* method produces a higher stability anti2 conformer, since its energy is 2 x 103 kcal/mol lower than the HF/3-21G counterpart. However, since different basis sets are employed it is rather unfair to compare the energies from each optimisation, so the geometries of the anti2 conformers will be compared instead.
The bond lengths are quite similar to each other, but it is interesting to note that the double bond lengths derived from the DFT/B3LYP/6-31G* optimisation are well in agreement to the literature values, whereas the single bond lengths for the HF/3-21G conformer correspond slightly better to the literature[1]. In addition to this, the DFT/B3LYP/6-31G* method generates larger dihedral angles, particularly seen by the first and third angles. This highlights the significance of conducting calculations at a higher level theory to obtain a more accurate impression of the geometry of the minimum energy conformer.
Frequency Analysis
Frequency analysis is the second derivative of the potential energy curve, thus, it is imperative to run in order to identify the success of the calculation. The system is at a minimum when all frequencies computed are positive; if one frequency is negative, the system has reached a transition state; if there are more than one negative frequencies, the calculation has failed to find a critical point.

What’s more, frequency analysis provides a means to compare calculated energies with experimental quantities. The DFT/B3LYP/6-31G* method will be employed to conduct such analysis.
| Form of Energy | at 298.15 K (/Hartrees) | at 0 K (/Hartrees) | ΔE, 298.15 K - 0 K (/Hartrees) | ΔE, 298.15 K - 0 K (/kcal mol-1) |
| Sum of electronic and zero-point energies | -234.469204 | -234.468767 | -4.37 x 10-4 | -6.55 x 10-2 |
| Sum of electronic and thermal energies | -234.461857 | -234.461431 | -4.26 x 10-4 | -6.38 x 10-2 |
| Sum of electronic and thermal enthalpies | -234.460913 | -234.460487 | -4.26 x 10-4 | -6.38 x 10-2 |
| Sum of electronic and thermal free energies | -234.500777 | -234.500328 | 4.49 x 10-4 | -6.74 x 10-2 |
By studying the above table, it is evident that the anti2 conformer is slightly more stable at room temperature than at absolute zero, with respect to all types of energies. The sum of electronic and zero-point energies is somewhat constant for both temperatures, which is expected since E=Eelec + ZPE. The electronic and thermal energies and enthalpies are more negative at the higher temperature due to the addition of the positive thermal corrections (RT= H – E) and/or the corresponding increased contributions from the translational, vibrational and rotational energy modes. The sum of electronic and thermal free energies shows the largest difference due to the entropic contribution to the free energy, which is dependent on temperature (i.e. G= H – TS). It is interesting to note how the IR spectra at the two differing temperatures scarcely change.
 |
 |
This exercise has depicted how informative frequency analysis can be, especially when acquiring relevant energies of molecules or transition structures. The methodology shows how one can adjust the temperature, pressure or isotopic mass in order to study possible kinetic or thermodynamic reactions under different conditions, which may not be experimentally viable.
Optimising the Transition States
The C2h chair and C2v boat transition states of the Cope Rearrangement will now be optimised via a selection of different methods that demonstrate various computational techniques.
The Chair TS
In order to optimise the chair transition state, an allyl, CH2CHCH2, fragment was drawn into Gaussview and optimised through the HF/3-21G method. The optimised structure was then copied and pasted twice into a new window, and aligned in a manner to resemble the chair transition state in Appendix 2. The distance between the terminal ends of the fragments was then set to 2.20 Å. An Opt+Freq calculation is then carried out on this guessed transition structure through the HF/3-21G method to a TS (Berny). The optimisation is achieved by calculating the force constants only once, while the keywords Opt=NoEigen prevents the calculation from crashing if the guess structure is too inaccurate, which would cause more than one imaginary frequency being detected.
The next method employs the Redundant Coordinate Editor on Gaussview, which freezes the coordinates of the two sets of terminal carbons (i.e. where the new σ-bond is formed and where the old σ-bond is broken during rearrangement), and minimises the rest of the molecule. This is achieved by defining these atoms as Bond→Freeze Coordinate, where the atom distances were also set to 2.2 Å. When the molecule is fully relaxed, the reaction coordinate can be unfrozen by changing Bond→Freeze Coordinate to Bond→Derivative. This can now be optimised once again to TS (Berny), but here the force constants are never calculated.
The data obtained from both methods are very similar, since both identify the same transition state. The minute difference in the energies and bond lengths is negligible. Computed vibrational frequencies are only accurate to the closest integer, implying that both methods produce an imaginary frequency at -818 cm-1. This vibrational mode shows an asynchronous bond formation, as evident by the C-C bond being formed whilst another C-C bond is being broken. This is expected for the pericyclic Cope Rearrangement. It is interesting to note how both methods generate the same/very similar results, even though they were derived from such different theories. The first method relies on calculating the force constant matrix (Hessian) in the first optimisation step, which is then recalculated during the remainder of the optimisation. On the other hand, the frozen coordinate method does not require calculating the whole Hessian; instead, the reaction coordinate must be differentiated in order to estimate the initial force constant matrix. This saves computing time, but the drawback occurs when the guessed structure is not accurate enough.
The Boat TS
The boat transition state will be optimised using the QST2 method, which derives the transition structure by interpolating between the reactant and product molecules. The “anti2’’ 1,5-hexadiene conformer is opened up in two simultaneous windows, and orientated so that one acts as the reactant, whilst the other, the product. It is also vital that the atoms are manually labelled correctly for this technique, since a failure to number the carbons correctly could lead to producing the wrong transition structure. The Gaussian job was set to Opt+Freq to a TS (QST2) via the HF/3-21G method, but the calculation failed. This is because the calculation only considered translating the top allyl fragment; it did not consider the possibility of a rotation about the central carbon bonds. The resulting checkpoint file resembled a dissociated chair transition structure.
In order to overcome the failed calculation, the geometries of both the reactant and product structures had to be adjusted. In both molecules, the central C2- C3- C4- C5 dihedral angle was set to 0o, whilst the C2- C3- C4 and C3- C4- C5 angles were both set to 100o. The QST2 calculation was now ready to be performed again.

| Optimised TS Structure | |||
|---|---|---|---|
| Terminal C-C bond length (/Å) | 2.14042 / 2.14081 | ||
| Energy (/Hartrees) | -231.60280218 | ||
| Energy (kcal mol-1) | -1.45 x 105 | ||
| Imaginary frequency (cm-1) | -839.548 | ||
| Vibration | 
|
Intrinsic Reaction Coordinate
The Intrinsic Reaction Coordinate (IRC) allows one to follow the minimum energy path from the transition structure to its local minimum on a potential energy surface. This enables one to predict the structure each transition state will produce. The transition structures take incremental geometric steps in the direction of the steepest energy surface gradient, which creates a succession of points until the minimum is reached (i.e. zero gradient).
In this exercise, an IRC calculation will be performed on the “chair” transition state, where the reaction coordinate will be computed in the forward direction only, since the molecule is symmetric. The number of points along the IRC will be set to 50 to ensure a minimum has been reached post-calculation. However, two different calculations will be carried out: one which measures the force constant matrix only once and the other which measures it always.
| Calculated force constants once | Calculated force constants always | |||||
| Structure at the last point of the IRC | ||||||
| Number of Points along IRC | 26 | 47 | ||||
| Energy (/Hartrees) | -231.68908039 | -231.69166426 | ||||
| IRC Reaction Coordinate Graphs | 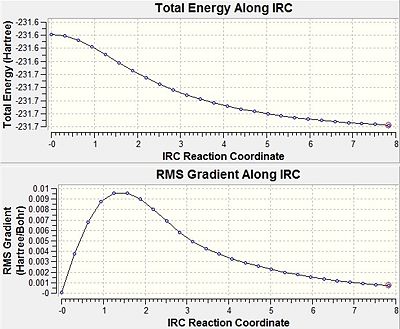 |

|
The initial method, where the force constant matrix was measured once, showed the calculation ending after the 26th cycle. The IRC calculation was evidently incomplete as the minimum on the potential energy surface was not reached. This can be seen by looking at the final step along the IRC pathway, which shows a failure to form an asymptote, as well as a RMS gradient relatively larger than zero. What’s more, the frequency analysis of the final step structure shows one imaginary frequency, thus, it is still a transition structure and a minimum has not been found.
In the second method, where the force constant matrix is measured at every step, the IRC calculation is able to distinguish whether it is moving along the minimum energy pathway; moreover, it can adjust the pathway while going down the potential energy surface when necessary. This method is computationally expensive, but it is more reliable than the first. The IRC reaches a minimum by the 47th step, which is seen by a near zero gradient and an asymptotic pathway. The 1,5-hexadiene minimum structure produced by the IRC calculation looked similar to the C2 gauche (gauche2) conformer, which is quantified by matching energies. The frequency analysis supports that the found minimum is in fact heading towards the gauche2 conformer, since real frequencies indicate a minimal energy structure. Therefore, this suggests that gauche2 is the geometry the chair transition state links.
| HF/3-21G | DFT/B3LYP/6-31G* | |||||
|---|---|---|---|---|---|---|
| Structure | Electronic energy (/Hartrees) | Sum of electronic and zero-point energies at 0 K (/Hartrees) | Sum of electronic and thermal energies at 298.15 K (/Hartrees) | Electronic energy (/Hartrees) | Sum of electronic and zero-point energies at 0 K (/Hartrees) | Sum of electronic and thermal energies at 298.15 K (/Hartrees) |
| anti2 (reactant) | -231.692535 | -231.539524 | -231.532562 | -234.611710 | -234.468767 | -234.461857 |
| Chair TS | -231.619322 | -231.466677 | -231.461320 | -234.556983 | -234.414929 | -234.409008 |
| Boat TS | -231.602802 | -231.450936 | -231.445303 | -234.543093 | -234.402342 | -234.396008 |
| Theory Level | HF/3-21G | HF/3-21G | B3LYP/6-31G* | B3LYP/6-31G* | Expt. |
| Temperature | at 0 K | at 298.15 K | at 0 K | at 298.15 K | at 0 K |
| ΔE Chair (/Hartrees) | 0.072854 | 0.073213 | 0.053838 | 0.054727 | - |
| ΔE Chair (kcal mol-1) | 45.716585 | 45.9418609 | 33.7838623 | 34.3417183 | 33.5 ± 0.5 |
| ΔE Boat (/Hartrees) | 0.088588 | 0.089733 | 0.066425 | 0.068617 | - |
| ΔE Boat (kcal mol-1) | 55.5898212 | 56.3083197 | 41.6823257 | 43.0578268 | 44.7 ± 2.0 |
The higher level theory, DFT/B3LYP/6-31G*, gives results which are much more consistent with the experimental findings, due to the more computationally expensive optimisations. However, generally the calculations are in accordance with the literature values. Since the chair transition state has a lower activation energy to that of the boat, it implies the Cope rearrangement occurs through the chair TS. Thus, the reactant initiates from the anti2 conformer, rearranges to yield the chair transition structure, and then goes onto forming the gauche2 conformer.
| Transition State | Chair | Boat | ||||||||||
| Theory Level | HF/3-21G | DFT/B3LYP/6-31G* | HF/3-21G | DFT/B3LYP/6-31G* | ||||||||
| Optimised Structure | ||||||||||||
| Labelled Structures |  |
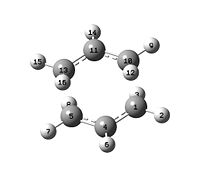 |
 |

| ||||||||
| Newly formed C-C bond length (/Å) | 2.02012 (C5-C13) / 2.01993 (C1-C10) | 1.96757 (C5-C13) / 1.96756 (C1-C10) | 2.14081 (C3-C4) / 2.14042 (C1-C6) | 2.20663 (C3-C4 and C1-C6) | ||||||||
| Internal C=C bond length (/Å) | 1.38931 / 1.38936 / 1.38943 / 1.38926 | 1.40750 | 1.38128 / 1.38134 / 1.38127 / 1.38135 | 1.39323 | ||||||||
| Fragment angle (/o) | 120.51244 (C1-C4-C5) | 119.95410 (C1-C4-C5) | 121.67887 (C1-C2-C3) | 122.27010 (C1-C2-C3) | ||||||||
Diels Alder Reactions
The methods and techniques learnt in the previous exercise will be used to now study the Diels-Alder reaction between cis-butadiene and ethylene. The cycloaddition proceeds through a single cyclic, concerted transition state, where two σ-bonds are formed between the conjugated diene and dienophile. Hence, the process is classified as a [4s+2s] cycloaddition, due to the number of π-electrons involved in the process. The number of π-electrons also helps determine whether the reaction progresses via a Huckel transition state or a Mobius TS, as only the Huckel topology will be allowed by the system.

The π-orbitals from the ethylene (i.e. the dienophile) form new σ-bonds to the π-orbitals of the butadiene molecule (the diene). In terms of molecular orbitals, this is possible since the HOMO/LUMO of one fragment interacts with the HOMO/LUMO of the other fragment to create one bonding and one anti-bonding MO. When the HOMO of one reactant interacts with the LUMO of the other reactant, the reaction is allowed. However, in order for an adequate interaction, there must be significant overlap density between the two orbitals. If the two orbitals have different symmetry properties, the reaction will be forbidden since there is no overlap density. The nodal properties of the molecular orbitals assist in predicting how the cycloaddition will occur.
The reactant structures of the Diels-Alder cycloaddition, cis-butadiene and ethylene, were drawn into Gaussview and initially optimised through the semi-empirical/AM1 method. Whilst this optimisation method provides a decent starting point, the theory level will be later be increased to DFT/B3LYP/6-31G* in order to obtain more reliable, accurate results. The QST2 optimisation will not be revisited in this exercise because this technique requires labelling the carbon atoms of the reagents and product perfectly, which is very time consuming. Additionally, if the numbering is incorrect the calculation will fail. Without doubt, the high level theory of the DFT method will help determine how this reaction proceeds.
| Optimised Reagent | Energy of Molecule (/Hartrees) | Molecular Orbital | Qualitative MO | Computed MO | Symmetry with respect to the plane | Energy of MO (/Hartrees) |
| 0.04880164 | LUMO |  |
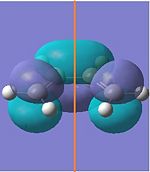 |
Symmetric | +0.017 | |
| HOMO |  |
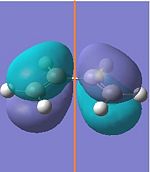 |
Anti-symmetric | -0.343 | ||
| 0.02619723 | LUMO |  |
 |
Anti-symmetric | +0.052 | |
| HOMO |  |
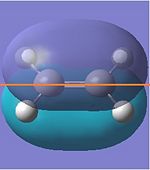 |
Symmetric | -0.387 |
Since the HOMO/LUMO symmetries for the two reagents are reversed, possible interactions can only occur between the cis-butadiene HOMO and the ethylene’s LUMO, or the cis-butadiene’s LUMO and the ethylene HOMO. This will ensure significant overlap density, which will allow the reaction to proceed. Moreover, the conservation of orbital symmetry states that the symmetry of a new orbital formed by the overlap of two orbitals must remain the same as the symmetry of the original orbitals.
Transition State Analysis
A guess transition structure was set up in Gaussview, and the distances between the fragment termini were set to 2.2 Å, via the frozen coordinate technique. An Opt+Freq job was performed on the structure, using two different levels of theory: the semi-empirical/AM1 method and the DFT/B3LYP/6-31G* method. The frozen coordinate technique was run in a similar manner to en earlier exercise in this module; the new bonds formed are frozen and the remaining structure is optimised to a minimum, after this the coordinates are unfrozen and they too are optimised, but to a TS (Berny).
| Optimisation Method | ||
| Energy (/Hartrees) | 0.11162912 | -234.54389566 |
| Bond Lengths |  |

|
| Imaginary Frequency (/cm-1) | -956.13 | -525.822 |
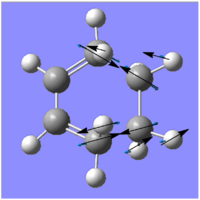 |
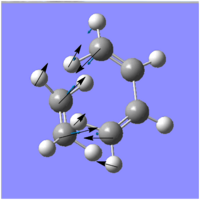
| |
| Lowest Real Frequency (/cm-1) | 146.863 | 135.675 |
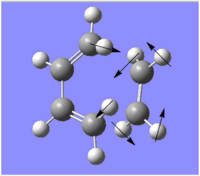 |
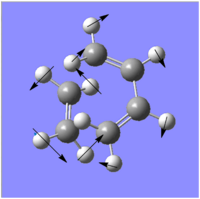
| |
| LUMO |  |
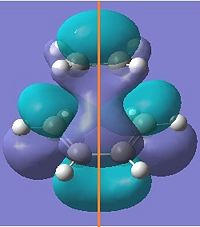
|
| HOMO | 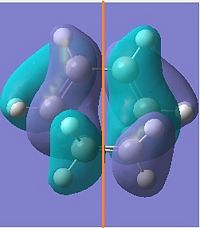 |
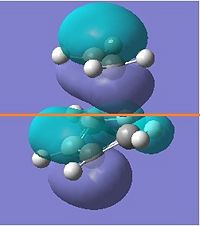
|
The new C-C bonds formed are reasonably longer in the DFT calculations than the semi-empirical C-C bond lengths, by approximately 0.15 Å. The larger bond length signifies a lower potential energy gradient to the TS giving that transition state a reduced total energy. Hence the DFT/B3LYP/6-31G* calculation arrives at a more stable transition structure than the semi-empirical/AM1 optimised TS. However, when examining the two theories, both newly formed bonds within each method are very similar in length, suggesting the synchronous nature of the bond formation. This is reinforced by the imaginary vibrational mode, showing the concerted formation of the two new bonds, which is expected for the pericyclic Diels-Alder reaction.
The internal carbon bonds of the transition state reveal interesting observations too. The carbon single bonds are shorter than the literature sp3 C-C bond lengths of 1.54 Å[1] by 0.14 Å, whereas the double bonds are longer than the typical sp 2 C=C bond length of 1.34 Å[1], by 0.04 Å. The inconsistent bond lengths show that the carbons in the transition state do not show proper covalent bonding, but since the lengths are smaller than the sum of two carbon Van der Waals radii[2] (3.44 Å), it is clear the carbons do still share electron density.
The DFT/B3LYP/6-31G* method carries out calculations to a greater degree of accuracy, which has already been touched upon this module. Since the purpose of computational chemistry is to obtain the most realistic, accurate results without being too computationally expensive, the results obtained from the density functional theory will be adopted for the activation energy comparisons.
The transition state LUMO has an energy of +0.023 Hartrees and it is symmetric with respect to the plane, whilst the HOMO is anti-symmetric with respect to the plane and is stabilised by -0.323 Hartrees. If one examines the MO images in more detail, one can observe that the TS LUMO is constructed of the “cis-“butadiene LUMO and the ethylene HOMO. The HOMO of the TS originates from the HOMO of the “cis-“butadiene and the LUMO of ethylene. Both resulting MOs of the transition state have the same symmetries as the orbitals overlapping to form them, which conserves orbital symmetry. Thus, the TS HOMO and LUMO correspond to the σ-bonding and σ* anti-bonding orbitals respectively.
The TS HOMO shows The HOMO and LUMO orbitals of the two reactants align suprafacially, therefore the phase distribution of both orbitals match. Hence, the reaction is allowed. This is verified since it is a 6 π-electron procehttps://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:dior101&action=edit§ion=10ss (4n+2) which proceeds under thermal conditions. The reaction will progress in a disrotatory fashion via a Huckel topology; this would be demonstrated in a substituted system.
ΔE Analysis
In order to calculate the activation energy required for the reaction, the reagents were re-optimised using the higher level theory of DFT/B3LYP/6-31G*.
| DFT/B3LYP/6-31G* Optimised Molecule | Energy (/Hartrees) | |
| cis-Butadiene | -155.98595591 | |
| Ethylene | -78.58745828 | |
| cis-Butadiene and ethylene combined | -234.57341419 | |
| Transition structure | -234.54389566 | |
| Activation energy (ΔE / Hartrees) | 0.0295185 | |
| Activation energy (ΔE / kcal mol-1) | 18.52314236 |
The activation energy computed is in accordance to the literature findings at 0 K[3]). However, the computed calculations should be taken as a substitute for experimental findings, since Gaussian can easily produce errors when manipulating the data, as well as this the programme fails to deal with non-idealities.
Cyclohexa-1,3-diene Cycloaddition with Maleic Acid
In order to study the regioselectivity of the Diels-Alder reaction, the [4+2] cycloaddition of maleic anhydride with cyclohexa-1,3-diene will be studied. The reaction can lead to the formation of an endo or exo product, depending on the orientation of the fragments when they react.
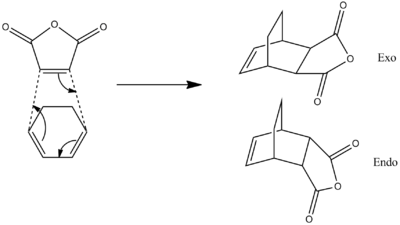
The reaction is kinetically controlled, hence, the outcome of the product is determined by the energy barrier to the reaction, which is found by studying the transition state energies. The reaction pathway with the lowest energy transition state will form the major product.
Both exo and endo transition states were drawn in Gaussview and an optimisation and frequency calculation was run. This was achieved by initially employing the semi-empirical/AM1 method and the frozen coordinate technique, which froze the forming bond distances to 2.2 Å. The bonds were unfrozen and optimised to a TS (Berny). Both TS were then re-optimised using the same method but a higher theory level of DFT/B3LYP/6-31G*; the additional keyword Opt=NoEigen ensured the calculation did not crash if more than one imaginary frequency was detected.
| - | exo | endo | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Semi-empirical/AM1 | DFT/B3LYP/6-31G* | Semi-empirical/AM1 | DFT/B3LYP/6-31G* | |||||||||
| Energy (/Hartrees) | -0.05041830 | -612.67931070 | -0.05150450 | -612.68339647 | ||||||||
| Structure | ||||||||||||
| C-C bond forming length (/Å) | 2.17 | 2.29 | 2.16 | 2.27 | ||||||||
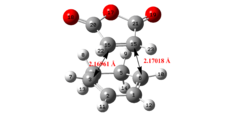 |
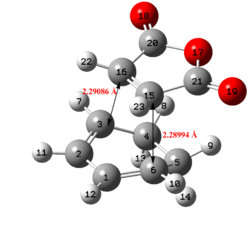 |
 |

| |||||||||
| Imaginary Frequency (/cm-1) | -812.983 | -448.555 | -806.423 | -446.623 | ||||||||
 |

| |||||||||||
Besides from the already noted differences in the varied theory levels, the C-C bond forming length between the two fragment termini are very similar in the endo and exo transition states. In addition to this, the imaginary vibrational mode shows that the bond forming in both reactions is synchronous, which is typical for the concerted Diels-Alder cycloadditions.
The endo TS is stabilised by approximately 2.56 kcal mol-1 compared to the exo TS. However, instinctively, this is not obvious. One would expect the exo TS to be more stable since it experiences less strain.
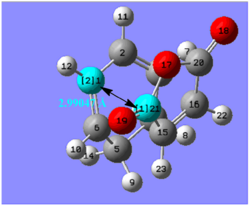
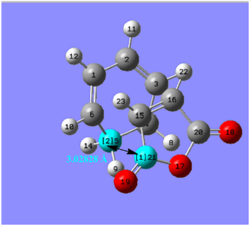
This is shown by the distance between the cyclohexa-1,3-diene ring and the –(C=O)-O-(C=O)- maleic anhydride fragment, which is 2.99 Å in the endo transition state and 3.03 Å in the exo TS. The smaller distance between the two bulky fragment groups should confer steric hindrance to the endo TS structure, therefore increasing its energy.
However, the vicinal hydrogens on the CH2-CH2 of the cyclohexa-1,3-diene ring are below the plane and next to the maleic anhydride, in the exo TS. This confers greater hindrance to the structure, counteracting any stability it achieved by being further away from the –(C=O)-O-(C=O)- fragment than the endo. Hence, the endo transition state is the more favourable of the two, rendering the endo product the major product of the reaction [4].
The preference for an endo TS as a kinetic effect is supported by secondary orbital overlap too. This involves the frontier orbitals that are not directly involved in forming the bonds in the reaction, instead they interact with each other through space. In the endo TS there are additional orbital interactions that result to the stabilisation of the transition state.

One may assess the molecular orbitals to check if they are in agreement with the previous discussion.
| Molecular Orbital | exo | endo | ||||
|---|---|---|---|---|---|---|
| Semi-empirical/AM1 | DFT/B3LYP/6-31G* | Symmetry with respect to plane | Semi-empirical/AM1 | DFT/B3LYP/6-31G* | Symmetry with respect to plane | |
| LUMO | 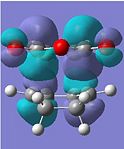 |
 |
Anti-symmetric | 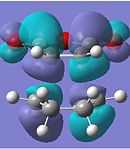 |
 |
Anti-symmetric |
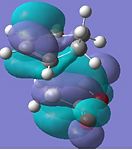
| HOMO | 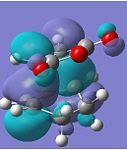 |
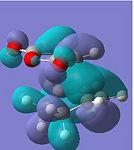 |
Anti-symmetric | 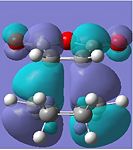 |
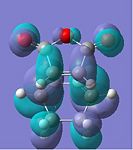 |
Anti-symmetric |
| HOMO-1 | 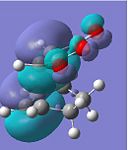 |
 |
Anti-symmetric |  |
 |
Anti-symmetric |
The HOMOs of both transition states symbolise the σ-bonding, which is formed between the two reactants. However, the HOMO of the endo TS fails to show any significant secondary orbital overlap, which is expected. Instead, in the HOMO-1 of the endo TS, the oxygen atoms from the maleic anhydride seem to interact with the forming π-bond. This may increase the stabilisation of the endo TS, since in the exo transition structure, the forming π-bond is geometrically unavailable for any form of secondary interactions.
Conclusion
To conclude, computational methods have provided an accessible and somewhat reliable means to predict the reaction pathways studied in this module. If one was able to use more computationally expensive calculations, it is no wonder why there is a growing interest in this field of chemistry.
References
- ↑ 1.0 1.1 1.2 G. Schultz, I. Hargitta, J. Mol. Struc., 1995, 346, pp. 63-69.[1]
- ↑ M. Mantina, A. C. Chamberlin, R. Valero, C. J. Cramer, D. G. Truhlar, 1995, 346, pp. 63-69.[2]
- ↑ V. Guner, K. S. Khuong, A. G. Leach, P. S. Lee, M. D. Bartberger, K. N. Houk, J. Phys. Chem. A, 2003, 107 (51), pp. 11445–11459.[3]
- ↑ Ian. Fleming, Frontier Orbitals and Organic chemical reaction, John Wiley and Sons Ltd., 1976, p.106-109
Digital Repositories
- IRC (always) DOI:10042/to-6244
- IRC (once) DOI:10042/to-6245
- DFT/B3YLP/6-31G* exo DOI:10042/to-6246
- DFT/B3YLP/6-31G* endo DOI:10042/to-6247
- Semi-empirical/AM1 exo DOI:10042/to-6248
- Semi-empirical/AM1 exo DOI:10042/to-6249


