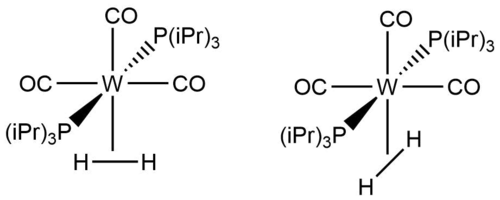Rep:Mod:dialekticnomaterialisticen
NH3
Optimisation Setup
Calculation Method: B3LYP
Basis set: 6-31G(d,p) - medium accuracy
Type of calculation: OPTF
Optimisation Results
Calculation method: RB3LYP
Type of calculation: FREQ
Basis set: 6-31G(d,p)
Total Energy (RB3LYP): -56.55776 a.u.
RMS Gradient: 0.00000485 a.u.
Dipole Moment: 1.8467 D
Point Group: C3v
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
The optimisation file can be found here.
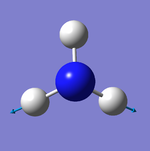
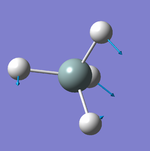
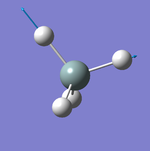
Geometry of the Optimised Molecule
Bond Length: 1.02 Å
H-N-H Bond Angle: 106°
Optimised ammonia molecule |
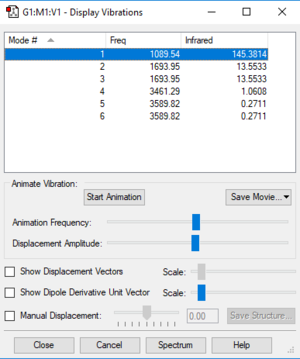
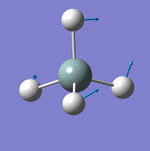
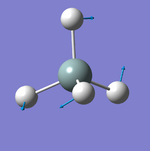
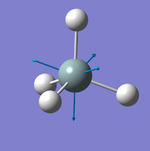
Vibrations Display
Vibration Analysis
| wavenumber (cm-1 | symmetry | intensity (a.u.) | image | vibration type | notes |
|---|---|---|---|---|---|
| 1090 | A1 | 145 |  |
bending | "umbrella" mode |
| 1694 | E | 14 |  |
bending | degenerate |
| 1694 | E | 14 |  |
bending | |
| 3461 | A1 | 1 |  |
stretching | highly symmetric |
| 3590 | E | 0 |  |
stretching | degenerate |
| 3590 | E | 0 |  |
stretching |
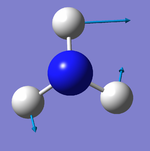
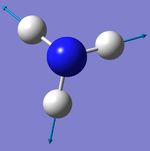
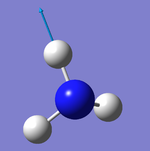
The number of vibrational modes for a non-linear molecule is 3N - 6, where N is the number of atoms in the molecule. For ammonia N = 4, and we expect to see 6 vibrational modes. Our computational analysis found all 6 of them.
Compared to this calculation, an experimental IR spectrum of NH3 would only show two bands. A strong band would be seen for the vibration at 1090 cm-1, and a weak band for the two degenerate vibrations at 1694 cm-1. The three "stretching" vibrations would not be observed as their intensity is too low.
Charge distribution
Dipole moment: 1.8466 D
Charge on N atom: -1.125 e
Charge on H atom: 0.375 e
As expected nitrogen, the more electronegative element, has the negative charge, while the positive charge is distributed over the hydrogen atoms. This is due to nitrogen atoms having a higher effective nuclear charge and therefore exhibit a stronger attraction towards electrons in the hydrogen 1s orbital.
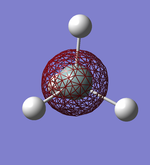
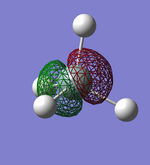
Molecular Orbitals
| Image | Energy (eV) | Contributing AO | Bonding character | Ground state e- | other |
|---|---|---|---|---|---|
 |
-14.31 | N 1s | non-bonding | occupied | |
 |
-0.84 | N 2s + 3x H 1s | bonding | occupied | |
 |
-0.45 | N 2px +3x H 1s | bonding | occupied | degenerate |
 |
-0.45 | N 2py + 3x H 1s | bonding | occupied | |
 |
-0.25 | N 2pz + 3x H 1s | bonding | occupied | HOMO |
This shows what orbitals actually look like, compared to hybridisation which is just a mathematical tool. Combining all but the orbital in the first row of the table is equivalent to combining the 4 sp3 orbitals.
N2
Optimisation Setup
Calculation Method: B3LYP
Basis set: 6-31G(d,p)
Type of calculation: OPTF
Optimisation Results
Calculation Method: RB3YLP
Basis set: 6-31G(d,p)
Total Energy (RB3LYP): -109.52413 a.u.
RMS Gradient: 0.00000060 a.u.
Dipole Moment: no
Point Group: D∞h
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
The optimisation file can be found here.
Geometry of the Optimised Molecule
Bond Length: 1.11 Å
Optimised nitrogen molecule |
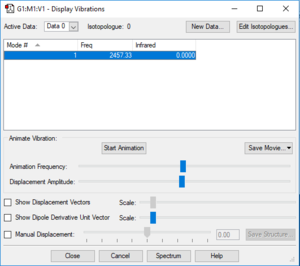
Vibrations Display
Vibration Analysis
| wavenumber (cm-1 | symmetry | intensity (a.u.) | image | vibration type | notes |
|---|---|---|---|---|---|
| 2457 | SGG | 0 |  |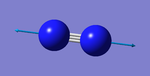
stretching | not IR active |
Charge distribution
Dipole moment: 0
Charge on N atom: 0
N2 is a homonuclear diatomic molecule. This results in it having no dipole moment. Additionally, stretching the bond does not produce a change in the dipole moment and the molecule is therefore IR inactive.
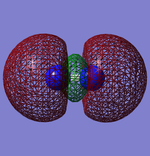
Molecular Orbitals
| Image | Energy (eV) | Contributing AO | Bonding character | Ground state e- | other |
|---|---|---|---|---|---|
 |
-14.45 | 2x N 1s | weakly bonding | occupied | |
 |
-14.45 | 2x N 1s | weakly anti-bonding | occupied | |
 |
-1.12 | 2x N 2s | bonding | occupied | |
 |
-0.55 | 2x N 2s | anti-bonding | occupied | |
 |
-0.46 | 2x N 2p | bonding | occupied | 2 degenerate orbitals |
 |
-0.43 | 2x N 2pz | bonding | occupied | HOMO |
 |
-0.02 | 2x N 2p | anti-bonding | empty | 2 degenerate orbitals, LUMO |
 |
0.41 | 2x N 2pz | anti-bonding | empty |
This confirms what we learned in the Chemical Bonding and Structure course. Due to the 2s and 2p orbitals in nitrogen being close enough in energy orbital mixing occurs, which results in the two degenerate π bonding orbitals having an energy of -0.46 eV compared to the bonding σ orbital with an energy of -0.43 eV.
H2
Optimisation Setup
Calculation Method: B3LYP
Basis set: 6-31G(d,p)
Type of calculation: OPTF
Optimisation Results
Calculation Method: RB3YLP
Basis set: 6-31G(d,p)
Total Energy (RB3YLP): -1.17854 a.u.
RMS Gradient: 0.00000017
Dipole Moment: no
Point Group: D∞h
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
The optimisation file can be found here.
Geometry of the Optimised Molecule
Bond Length: 0.74 Å
Optimised hydrogen molecule |
Vibrations Display
Vibration Analysis
| wavenumber (cm-1 | symmetry | intensity (a.u.) | image | vibration type | notes |
|---|---|---|---|---|---|
| 4466 | SGG | 0 |  |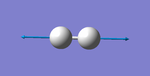
stretching | not IR active |
Charge distribution
Dipole moment: no
Charge on H atom: no
H2 is a homonuclear diatomic molecule. This results in it having no dipole moment. Additionally, stretching the bond does not produce a change in the dipole moment and the molecule is therefore IR inactive.
Molecular Orbitals
| Image | Energy (eV) | Contributing AO | Bonding character | Ground state e- | other |
|---|---|---|---|---|---|
 |
-0.43 | 2x H 1s | bonding | occupied | HOMO |
 |
0.10 | 2x H 1s | anti-bonding | empty | LUMO |
Coordination in a Transition Metal Complex
Adapted from IChO 2019 Preparatory Problem no. 5.
In the Kubas complex (σ2-Dihydrogen)-tricarbonyl-bis(tri-isopropylphosphine)-tungsten (CEJDEA), one of the ligands is a H2 molecule. The H-H bond length in this ligand molecule is 0.755 Å, compared to the usual 0.74 Å in gaseous dihydrogen.
The complex offers two different orientations of H2. The H-H bond can either be parallel to the OC-W-CO bond (y-axis) or the P-W-P bond (x-axis). If we consider the dehydrogenated complex as a square pyramidal structure we can assign the energy order of the d-orbitals due to ligand splitting as:
dxy < dyz < dxz < dz2 < dx2-y2
This is due to the CO ligand splitting the d-orbitals more strongly than P(iPr)3.
We can explain the bonding of H2 to the complex by considering the possible orbital overlap of the d-orbitals with the σ and σ* orbitals of H2. The σ orbital can interact with the eg orbitals and the σ* orbital can interact with the t2g orbitals of the complex. As the σ orbital shares some of its electron density with the eg orbitals the H-H bond is weakened and therefore longer. A longer bond also ensures more optimal overlap with the much larger 5d orbitals.
Analysing the complex according to crystal field theory gives us some information on the bonding, but tells us little about the orientation of H2. CO is a strongly splitting ligand, but so is P(iPr)3. The overall energy difference in the orbital interactions would therefore be small, but would favour H-H being along the P-W-P axis (orbitals more available). But P(iPr)3 can represent a steric obstacle for H2 and this could overcome the difference in ligand strength. As W is in row 6 of the periodic table, where rules of thumb aren't the most effective anymore, we can't exclude the potential interaction of the W 6s orbital. A way of determining what the favoured configuration of the complex is, is performing an energy minimisation calculation of the complex.
[I submitted the structure of the complex to Gaussian trying to perform an optimisation of energy only - Gaussian aborted the process every time after a few seconds with: Sever Error Message # 2070. I couldn't do this calculation in time for the lab submission, but would love to have someone explain to me where I went wrong in setting up the calculation.]
Investigation of H2 as a ligand has a practical application. Storing hydrogen in a complex as the one above provides an alternative to storing it as a highly compressed gas or a liquid that requires very low temperatures. The complex investigated here only stretches the H-H bond by a small amount, indicative of a relatively weak interaction. Practically, the complex easily dissociates and is also easily regenerated.
Haber-Bosch Process Energy Calculation
E(NH3) = -56.55777 a.u.
2 * E(NH3) = -113.11554 a.u.
E(N2) = -109.52413 a.u.
E(H2) = -1.17854 a.u.
3 * E(H2) = -3.53562 a.u.
ΔE = 2 * E(NH3) - [E(N2) + 3 * E(H2)] = -0.05579 a.u. = -146.5 kJ mol-1
The calculation shows that the product (ammonia) has a lower energy than the reactants (nitrogen and hydrogen gas) and is therefore more stable. The calculated value is quite a bit larger than the enthalpy of the Haber-Bosch process (approx - 90 kJ/mol). This is a combined result of small errors in the individual optimisations and is expected.
Silane SiH4
Optimisation Setup
Calculation Method: B3LYP
Basis set: 6-31G(d,p)
Type of calculation: OPTF
Optimisation Results
Calculation Method: RB3YLP
Basis set: 6-31G(d,p)
Total Energy (RB3LYP): -291.88803 a.u.
RMS Gradient: 0.00000003 a.u.
Dipole Moment: no
Point Group: Td
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
The optimisation file can be found here.
Geometry of the Optimised Molecule
Si-H Bond Length: 1.48 Å
Optimised H-Si-H Bond Angle: 110 °
Optimised silane molecule |
Vibrations Display
Vibration Analysis
| wavenumber (cm-1 | symmetry | intensity (a.u.) | image | vibration type | notes |
|---|---|---|---|---|---|
| 919 | T2 | 136 |  |
bending | degenerate |
| 919 | T2 | 136 |  |
bending | |
| 919 | T2 | 136 |  |
bending | |
| 979 | E | 0 |  |
bending | degenerate, IR inactive |
| 979 | E | 0 |  |
bending | |
| 2244 | A1 | 0 |  |
stretching | IR inactive |
| 2255 | T2 | 143 |  |
stretching | degenerate |
| 2255 | T2 | 143 |  |
stretching | |
| 2255 | T2 | 143 |  |
stretching |
From 3N - 6 we get 9 vibrations, as seen in the table above. Two bands of approximately the same strength would be seen in the IR spectrum of silane. One at 919 cm-1 and one at 2255 cm-1 for both triples of degenerate vibrations. The other vibrations are IR inactive.
Charge distribution
Dipole moment: 0
Charge on Si atom: 0.629 e
Charge on H atom: -0.157 e
Si is more electropositive than H and in this case therefore the negative charge is spread over the H, and Si has a partial positive charge.
Compare this to the charges in methane (calculated and confirmed using the same calculations as for all other molecules on this wiki) where the charge on C is -0.930 and +0.233 on each H. The reversed bond polarity in silane compared to methane gives it some interesting properties. E.g. silane is pyrophoric - it undergoes spontaneous combustion in air, while methane requires an outside source for ignition.
Molecular Orbitals
| Image | Energy (eV) | Contributing AO | Bonding character | Ground state e- | other |
|---|---|---|---|---|---|
 |
-5.28 | Si 2s | non-bonding | occupied | |
 |
-3.64 | Si 2p | non-bonding | occupied | 3 degenerate orbitals |
 |
-0.55 | Si 3s + 4x H 1s | bonding | occupied | |
 |
-0.35 | Si 3p + 4x H 1s | bonding | occupied | 3 degenerate orbitals, HOMO |
 |
0.05 | Si 3p + 4x H 1s | anti-bonding | empty | 3 degenerate orbitals, LUMO |
 |
0.12 | Si 3s + 4x H 1s | anti-bonding | empty |
Marking
Note: All grades and comments are provisional and subject to change until your grades are officially returned via blackboard. Please do not contact anyone about anything to do with the marking of this lab until you have received your grade from blackboard.
WELL DONE! Very nice wiki, good work. If you would like to know what went wrong with your complex calculation please send the .com file and the .log file to me! (rr1210@ic.ac.uk)
Wiki structure and presentation 1/1
Is your wiki page clear and easy to follow, with consistent formatting?
YES
Do you effectively use tables, figures and subheadings to communicate your work?
YES
NH3 1/1
Have you completed the calculation and given a link to the file?
YES
Have you included summary and item tables in your wiki?
YES
Have you included a 3d jmol file or an image of the finished structure?
YES
Have you included the bond lengths and angles asked for?
YES
Have you included the “display vibrations” table?
YES
Have you added a table to your wiki listing the wavenumber and intensity of each vibration?
YES
Did you do the optional extra of adding images of the vibrations?
YES
Have you included answers to the questions about vibrations and charges in the lab script?
YES
N2 and H2 0.5/0.5
Have you completed the calculations and included all relevant information? (summary, item table, structural information, jmol image, vibrations and charges)
YES
Crystal structure comparison 0.5/0.5
Have you included a link to a structure from the CCDC that includes a coordinated N2 or H2 molecule?
YES
Have you compared your optimised bond distance to the crystal structure bond distance?
YES
Haber-Bosch reaction energy calculation 1/1
Have you correctly calculated the energies asked for? ΔE=2*E(NH3)-[E(N2)+3*E(H2)]
YES
Have you reported your answers to the correct number of decimal places?
YES
Do your energies have the correct +/- sign?
YES
Have you answered the question, Identify which is more stable the gaseous reactants or the ammonia product?
YES
Your choice of small molecule 5/5
Have you completed the calculation and included all relevant information?
YES
Have you added information about MOs and charges on atoms?
YES
Independence 1/1
If you have finished everything else and have spare time in the lab you could: Check one of your results against the literature, or Do an extra calculation on another small molecule, or Do some deeper analysis on your results so far
You did lots of independent work well done!