Module 3 - Transition States and Reactivity

This module is an exploration of the techniques available in gaussian to model transition states and qualify reactivity in terms of these transition states. In the first section the Cope Rearrangement of 1,5-hexadiene is examined, and in the second section the diels-alder reaction will be scruitinised.

Part 1(i) Cope Rearrangement of 1,5-hexadiene: Conformers of 1,5-hexadiene

The cope rearrangement is a [3,3] sigmatropic rearrangement; a thermally activated pericyclic reaction. In most cases a single, lower energy product will be the major product, however in this report it is a degenerate isomerisation with both starting material and product of equal energy.

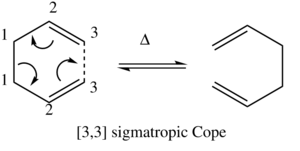
This reaction was studied to explore transition states and their computational accesibility, and to explore the usefulness of computational chemistry in conformational analysis.

Optimisation of 1,5-hexadiene

A molecule of 1,5-hexadiene was drawn in guassview with an approximately anti-periplanar linkage. The molecule was cleaned using the clean tool and optimised at the 3-21G level.

Anti-Periplanar C_i
File type/link	.chk
Calculation type	FOPT
Method	RHF
Basis Set	3-21G
Energy (au)	-231.6925351
Gradient (au)	0.00003372
Point Group	C_i
Calculation Duration (min)	0.62

A second molecule was drawn in gaussview, this time with an approximately gauche linkage, cleaned and optimised at the 3-21G level.

Gauche C₁
File type/link	.chk
Calculation type	FOPT
Method	RHF
Basis Set	3-21G
Energy (au)	-231.6926612
Gradient (au)	0.00000588
Point Group	C₁
Calculation Duration (min)	0.62

The energies obtained are consistant with those found in appendix 1 of the lab script to 5 decimal places.

One might expect that the anti-periplanar conformation would be lowest in energy, by placing the most sterically demanding groups furthest away from each other. In fact, it is observed that gauche conformation shown above is lower in energy by 0.079 kcal.mol^-1. This demonstrates the importance of electronic effects when considering conformational analysis, which can usurp the purely steric factors.

The anti-periplanar molecule of C_i symmetry was subsequently optimised at the higher level 6-31G basis set.

Anti-Periplanar C_i
File type/link	.chk
Calculation type	FOPT
Method	RB3LYP
Basis Set	6-31G(d)
Energy (au)	-231.6117050
Gradient (au)	0.00001370
Point Group	C_i
Calculation Duration (min)	0.62

Comparison of Data

Anti-Periplanar C_i comparison
Atoms	3-21G Bond Length	6-31G(d) Bond Length
1(C) - 2(H)	1.0747	1.0885
1(C) - 1(H)	1.0734	1.0869
1(C) - 2(C)	1.3162	1.3335
2(C) - H(3)	1.0769	1.0919
C(2) - C(3)	1.5090	1.5042
C(3) - H(4)	1.0848	1.0980
C(3) - H(5)	1.0856	1.0997
C(3) - C(4)	1.5527	1.5482
C(4) - H(6)	1.0856	1.0997
C(4) - H(7)	1.0848	1.0980
C(4) - C(5)	1.5090	1.5042
C(5) - H(8)	1.0769	1.0919
C(5) - C(6)	1.3162	1.3335
C(6) - H(9)	1.0734	1.0869
C(6) - H(10)	1.0747	1.0885

Anti-periplanar C_i Anlysis
Atoms	3-21G Bond Angles	6-31G(d) Bond Angles
H(1) - C(1) - H(2)	116.31	116.47
H(1) - C(1) - C(2)	121.82	121.67
H(3) - C(2) - C(3)	115.52	115.71
C(2) - C(3) - H(4)	109.98	109.77
C(2) - C(3) - H(5)	109.98	109.79
H(4) - C(3) - C(4)	109.40	109.61
H(5) - C(3) - C(4)	108.34	108.19
C(3) - C(4) - H(6)	108.34	108.19
C(3) - C(4) - H(7)	109.40	109.61
H(6) - C(4) - H(7)	107.71	106.65
H(6) - C(4) - C(5)	109.98	109.79
H(7) - C(4) - C(5)	109.98	109.77
C(4) - C(5) - H(8)	115.52	115.71
H(8) - C(5) - C(6)	119.67	118.97
C(5) - C(6) - H(9)	121.87	121.86
C(5) - C(6) - H(10	121.82	121.67

It can be observed that variations in the bond lengths are of the order of 0.01 Å, and variations in bond angles of the order of 0.2°. These are relatively insignificant when considered in terms of the molecule. Of much greater importance, however, is the change in calculated energies. The calculation run at 3-21G places the molecule 50.72 kcal.mol^-1 lower in energy than the 6-31G optimisation, demonstrating the importance of appropriately chosen basis sets.

Frequency Analysis

With the consequent uncertainty driven by variation between basis sets it's very useful to have an experimentally measurable quantity. Gaussian can calculate the vibrational spectrum of molecules, as has been carried out here for the anti-periplaner conformer. Along with the vibrations shown in the image below, a set of numbers is also obtained from the .log file (included here).

 Sum of electronic and zero-point Energies=           -234.469218
 Sum of electronic and thermal Energies=              -234.461860
 Sum of electronic and thermal Enthalpies=            -234.460916
 Sum of electronic and thermal Free Energies=         -234.500844

These provided more detailed energetics on the molecule. The first number is the potential energy at 0 K, including the zero-point energy. The second is the energy at 298.15 K and 1 atm pressure taking into account the concomitant rotational,vibrational and translational energies. The third contains a correction for RT (H = E + RT), and the last one contains the entropic contribution to the free energy (G = H - TS)

Part 1(ii) Cope Rearrangement of 1,5-Hexadiene: Finding the Transition State

Chair Transition State - Hessian Method

The transition state can be considered as two CH₂CHCH₂ allyl fragments partially bonded to one another.

This allyl fragment was drawn in gaussview and optimised at the HF/3-21G level.

Allyl Fragment CH₂CHCH₂
File type/link	.chk
Calculation type	FOPT
Method	UHF
Basis Set	3-21G
Energy (au)	-115.8230400
Gradient (au)	0.0000235
Point Group	C2v
Calculation Duration (min)	0.43

The optimised fragment was then copied and pasted twice into a new molecule group and manually manipulated to resemble the chair transition state. The terminal carbons were set approximately 2.2 Å apart and a calculation set up to optimise the molecule to a transition state.

The transition state is a peak of the potential energy surface that corresponds to the lowest energy barrier the molecule must pass through in order for the reaction to proceed. In this method, the force constant matrix (or Hessian) is calculated at the beginning of the computation to inform on the direction of negative curvature, and thus guide through the reaction coordinate. This requires the starting structure to be sufficiently similar to the transition state otherwise the potential energy surface will be so dissimilar as to cause the computation to proceed in the wrong direction.

The Opt+Freq calculation was run at HF/3-21G and is summarised below:

Chair Transition State
File type/link	.chk
Calculation type	FREQ
Method	RHF
Basis Set	3-21G
Energy (au)	-231.6193216
Gradient (au)	0.0000529
Point Group	C2h
Calculation Duration (min)	0.1

Bond length between the allyl fragments was 2.02 Å and a frequency of -818 cm^-1 was obtained corresponding to the transition state shown below.

Chair Transition State Bond-Freezing Method

This method uses the ability to freeze bonds between fragments, to effectively allow two simultaneous optimisations, followed by a calculation of the transition state.

The allyl fragments were once again aligned in an aproximately chair conformation. They were manipulated such that the terminal carbons were approximately 2.2 Å away from the other fragment, and the bonds frozen in the redundant coordinate editor. These are optimised at the HF/3-21G level.

Chair Transition State
File type/link	.chk
Calculation type	FOPT
Method	UHF
Basis Set	3-21G
Energy (au)	-231.6155863
Gradient (au)	0.0031609
Point Group	C_2h
Calculation Duration (min)	0.52

The frozen bonds are once again edited in the redundant coordinate editor to inform the computation to calculate the derivitive along the reaction coordinate (along this bond). Opt+Freq was run at HF/3-21G and the results summarised below.

Chair Transition State
File type/link	.chk
Calculation type	FOPT
Method	UHF
Basis Set	3-21G
Energy (au)	-231.6193222
Gradient (au)	0.0000300
Point Group	C_2h
Calculation Duration (min)	0.1

This method also produced an imaginary vibration of magnitude 818 cm^-1 shown below:

Boat Transition State QST2 Method

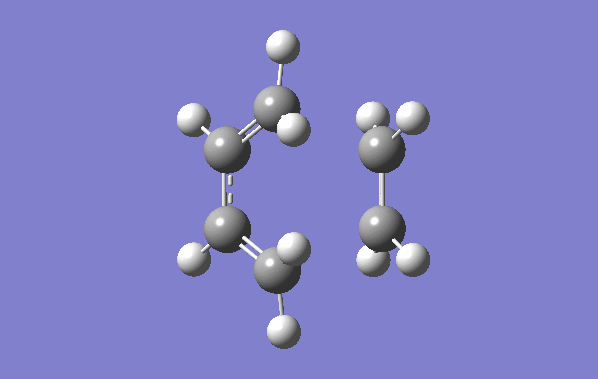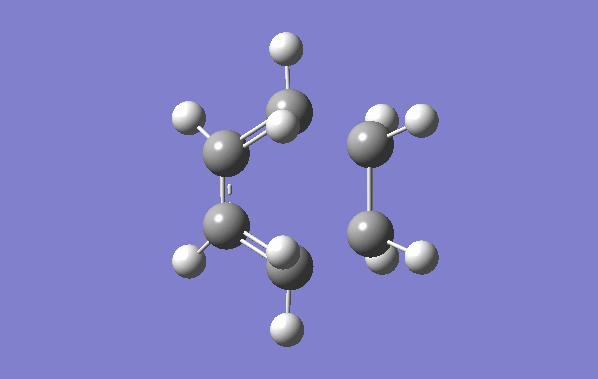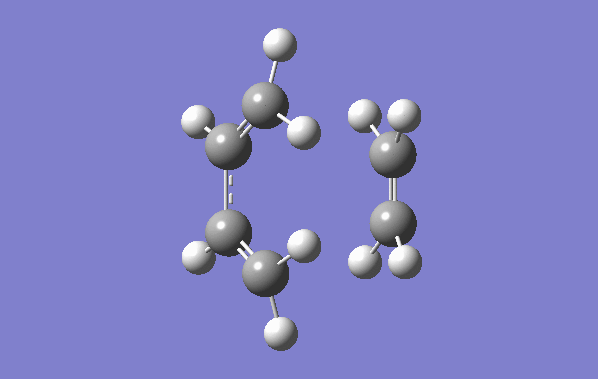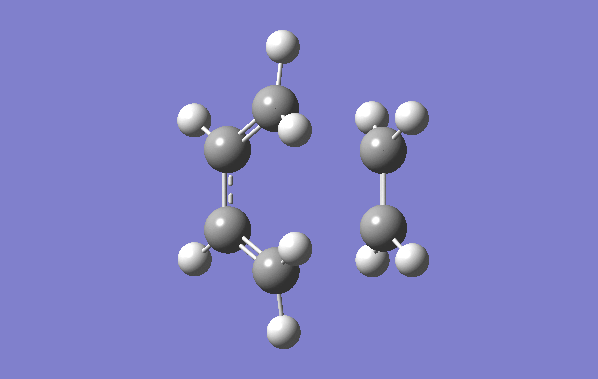
The QST2 method allows a transition state to be located between two molecules. The anti-periplanar molecule optimised from earlier was pasted twice into gaussview within the same molecule group. The numbering of the atoms was altered in the atom list so the two molecules corresponded to the reactants and products of a cope rearrangement as shown below:

The Opt+Freq QST2 calculation was run at the HF/3-21G level, however the structure obtained was not the expected product.

Boat Transition State
File type/link	.log
Calculation type	FREQ
Method	RHF
Basis Set	3-21G
Energy (au)	-231.4635038
Gradient (au)	0.0000148
Calculation Duration (min)	0.18

The calculation didn't consider rotation of the central carbon bonds and consequently gave an anomalous result. The input was altered manually changing the C2-C3-C4-C5 dihedral angle to 0° and the C2-C3-C4 and C3-C4-C5 angles to 100° and the calculation repeated.

Boat Transition State
File type/link	.log
Calculation type	FREQ
Method	RHF
Basis Set	3-21G
Energy (au)	-231.6028025
Gradient (au)	0.0000000
Calculation Duration (min)	0.58

This calculation gave an imaginary vibration of magnitude 840 cm^-1 that is shown below:

Part 1(iii) Cope Rearrangement of 1,5-hexadiene: Using the Intrinsic Reaction Coordinate

It is almost impossible to manually predict which conformers of 1,5-hexadiene are connected through the transition states calculated above. Theoretically, however, this can be acheieved by considering the gradient of the potential energy surface. The steepest slope from the transition state should reach a minimum at the conformer that passes through that transition state. The slope is accordingly measured at a designated interval (once at the beginning, or throughout the calculation) to try and guide the computation into the relevant minimum.

Chair IRC

The optimised chair transition state was loaded in gaussian, and a new calculation set up to run the IRC. The default points calculated was changed to 50 and the force constants were calculated at each step. While this is computationally more intensive it is a more reliable method than only calculating the force constants at the beginning. The direction was also set to forwards only, because the reaction is a rearrangement and symmetrical with respect to reaction coordinate from the transition state.

The computation was seen to converge in 44 steps and gave the gauche conformer 2 from appendix 1. The calculation summary, progress of the IRC and the final minimum conformer are shown below:

Chair Transition State IRC
File type/link	.log
Calculation type	FREQ
Method	RHF
Basis Set	3-21G
Energy (au)	-231.4635038
Gradient (au)	0.0000148
Calculation Duration (min)	0.18

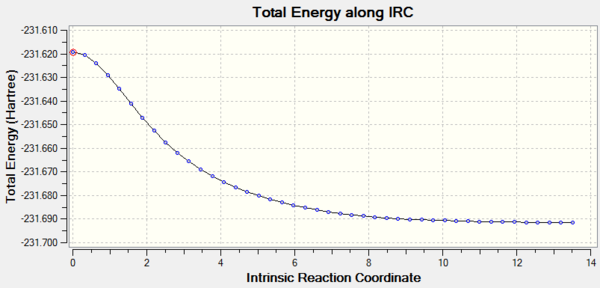
The path of the IRC can be understood visually from these graphs:

The total energy along the reaction coordinate decreases as we move down the potential energy surface from the high energy transition state through to the low energy well of optimised 1,5-hexadiene. The gradient, measured as root mean squared is initially maximised (first hump) before approaching zero at the stationary point of the minimum representing the gauche conformer above.

Using this data, the activation energy, E_a can be calculated by taking the difference in energy between the transition state and the relevant gauche conformer. It is found that at the HF/3-21G level, E_a = 45.34 kcal.mol^-1

As demonstrated earlier, however, the lower level basis sets such as those used here give a notably different energy to higher level basis sets such as 6-31G. The transition state and relevant conformer were then re-optimised at this higher level and E_a calculated again, this time to be 33.36 kcal.mol^-1. The literature value of 33.5 ± 0.5 kcal.mol^-1 ^[1] is in poor agreement with the lower level prediction, but excellent agreement with the more rigorous 6-31G treatment.

Boat IRC

The same method was undertaken for the boat transition state, at the 3-21G level with 100 points. The calculation converged in 45 steps and the results are summarised below:

Boat Transition State IRC
File type/link	.log
Calculation type	IRC
Basis Set	3-21G

The animation above at the 3-21G level shows that it is the same gauche conformer that passes through the boat transition state.

The reaction was run a second time at the 6-31G level, and was observed to converged after 70 iterations.

Boat Transition State IRC
File type/link	.log
Calculation type	IRC
Basis Set	6-31G

This higher level IRC calculation suggests it is a different conformer connected through the transition state, instead being the anti-4 conformer as labelled in appendix 1 of the lab script.

In both instances force constants were set to calculate always. The assumption is that the lower level basis set lacked the necessary precision to find the correct minimum, however just as 3-21G may have taken a mis-step, so too may 6-31G!

The calculated E_a for the two levels are:

3-21G E_a = 50.31 kcal.mol^-1

6-31G E_a = 41.66 kcal.mol^-1

Part 2(i) Diels-Alder Reaction of Butadiene and Ethene

The Diels-Alder reaction is a 4πs + 2πs pericyclic reaction proceeding via a concerted mechanism between a diene and a dieneophile. Pericyclic reactions can be categorised as either thermally or photochemically promoted, where each category can be rationalised in terms of orbital symmetry. A Thermally promoted pericyclic reaction occurs with conservation of orbital symmetry, while a photochemically driven pericyclic reaction occurs with inversion of orbital symmetry. This restriction for the Diels-Alder reaction dictates that the HOMO of the diene and the LUMO of the dieneophile be of the same symmetry.

First a molecule of butadiene was optimised using the semi-empirical AM1 basis set.

Butadiene
File type/link	.fchk
Calculation type	FOPT
Method	RAM1
Basis Set	ZDO
Energy (au)	0.0487853
Gradient (au)	0.0000028

Imagining a plane perpendicular to the C2-C3 bond, the butadiene HOMO is antisymmetric and the LUMO symmetric with respect to this plane.

Butadiene MOs
HOMO	LUMO


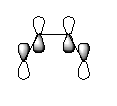
AS	S

Ethene by comparison has a symmetric HOMO and an antisymmetric LUMO.

The optimised butadiene fragment and an ethene fragment were positioned approximately in the correct position with ca. 2.2 Å between terminal carbons. The terminal positions were frozen in place using the redundant coordinate editor and the fragments initially optimised at the HF/3-21G level.

Butadiene
File type/link	.log
Calculation type	FOPT
Method	RHF
Basis Set	3-21G
Energy (au)	-231.6064802
Gradient (au)	0.0055469

Calculation of the transition state using the AM1 method was attempted at this point, however the computation failed. The fragment was then optimised at the HF/6-31G level

Butadiene
File type/link	.chk
Calculation type	FREQ
Method	RHF
Basis Set	6-31G
Energy (au)	-232.7995374
Gradient (au)	0.0000065

Calculation of the transition state using Opt+Freq at the AM1 level now succeeded, summarised below:

Butadiene
File type/link	.log
Calculation type	FREQ
Method	RAM1
Basis Set	ZDO
Energy (au)	0.1116556
Gradient (au)	0.0000676

An imaginary frequency of magnitude 956 cm^-1 was computed, shown below.

The transition state demonstrates the concerted, symmetric bond formation across the molecule to form cyclohexene.

The HOMO and LUMO of the transition state were also calculated and are plotted below.

Butadiene - Ethene Transition State MO


AS	S

It can be seen that the HOMO is, as expected, antisymmetric with respect to the plane outlined before.

A summary of the bond lengths obtained are shown below. The values in brackets are the literature values for the isolated compounds:

In areas where bond order decreases through the transition state there is significant lengthening compared to the isolated bond length. Conversely at sites where bond order increases through the transition state the is shortening compared to the literature values. The Van der Waals radius of for carbon is 1.70 Å, which along with the other data suggest the bonding is a hybrid between sp² and sp³. The symmetry of these bond lengths reflected in the plane bisecting the ethene bond also adds weight to the concerted mechanism of synchronous C-C σ-bond formation across the molecule, with bonds on either side lengthening or contracting equally.

According to Woodward-Hoffman rules, if the reaction proceeds with conservation of orbital symmetry it is "allowed" and thermally activated. This pericyclic reaction, with 4n+2 electrons (n = 1) falls into this category.

The intrinsic reaction coordinate can also be used in this case to follow the course of the reaction, however the asymmetry with respect to the transition state requires it be calculated in both directions.

Butadiene IRC
File type/link	.log
Calculation type	IRC
Method	RAM1
Basis Set	ZDO

Using the data obtained from the IRC calculation of activation energies is possible. In the Diels-Alder reaction between butadiene and ethene E_a calculated using the AM1 method was 23.24 kcal.mol^-1. This is in moderate agreement with a literature value of 25.1 kcal.mol^-1 at 0 K ^[2]

Part 2(ii) Diels-Alder Reaction of Cyclohexa-1,3-diene and Malaeic Anhydride

This Diels-Alder reaction poses an interesting question of selectivity. 2 Isomers can be formed in the reaction, summarised below:

Which isomer forms depends on if the reaction is under kinetic or thermodynamic control. This section will be an examination of the energetics of this reaction and a subsequent rationalisation of experimental data.

First the diene and the dieneophile were optimised using the AM1 method and the molecular orbitals plotted below.

Molecular Orbitals of Malaeic Anhydride and Cyclohexa-1,3-diene
Cyclohexa-1,3-diene HOMO	Cyclohexa-1,3-diene LUMO	Malaeic Anhydride HOMO	Malaeic Anhydride LUMO

AS	S	S	AS

As before, the transition states were calculated using the frozen bond method outlined earlier.

Exo Diels-Alder

The 2-fragment molecule was first optimised at the HF/3-21G level with bonds frozen in the redundant coordinate editor.

Exo-Diels Alder
File type/link	.log
Calculation type	FOPT
Method	RHF
Basis Set	3-21G
Energy (au)	-605.6044401
Gradient (au)	0.0026759

The frozen bonds were removed and a transition state calculated as before using the AM1 semi-empirical method.

Exo Diels Alder
File type/link	.log
Calculation type	FREQ
Method	RAM1
Basis Set	ZDO
Energy (au)	-0.0504184
Gradient (au)	0.0000451

An imaginary frequency of magnitude 812 cm^-1 was calculated corresponding to the synchronous C-C σ-bond formation. The vibration is shown below:

The molecular orbitals of the HOMO and LUMO were also plotted:

Molecular Orbitals of Malaeic Anhydride and Cyclohexa-1,3-diene Exo-Product
HOMO	LUMO

AS	AS

Forward and reverse IRC calculation was undertaken at the AM1 level and was used to calculate the activation energy for the reaction.

Exo-Diels Alder
File type/link	.log
Calculation type	IRC
Method	RAM1

The activation energy was calculated to be 28.21 kcal.mol^-1 using the AM1 method.

Endo Diels Alder

The Endo isomer was first optimised at the HF/3-21G level

Endo-Diels Alder
File type/link	.log
Calculation type	FOPT
Method	RHF
Basis Set	3-21G
Energy (au)	-605.5108821
Gradient (au)	0.0017313

The transition state was then calculated using the AM1 method

Endo-Diels Alder
File type/link	.log
Calculation type	FREQ
Method	RAM1
Basis Set	ZDO
Energy (au)	0.0515047
Gradient (au)	0.0000228

A frequency of -806 cm^-1 was calculated corresponding to the imaginary vibration below:

The following molecular orbitals were obtained for the transition state:

Molecular Orbitals of Malaeic Anhydride and Cyclohexa-1,3-diene Endo-Product
HOMO	LUMO

AS	AS

An IRC calculation was run in both directions and was seen to converge in 106 steps.

Endo-Diels Alder
File type/link	.log
Calculation type	IRC
Method	RAM1

An activation energy of 26.91 was calculated using the AM1 method.

Part 2(iii) - Diels-Alder Reaction of Cyclohexa-1,3-diene and Malaeic Anhydride Analysis of Results

In this reaction, as is often the case in chemistry, there are numerous effects each favouring a different isomer to varying extents.

The first effect to be considered is the effect of steric congestion, observable in the molecular orbitals of the transition state HOMOs.

Molecular Orbitals of Malaeic Anhydride and Cyclohexa-1,3-diene Endo-Product
ENDO	EXO

In the endo isomer there is a strongly anti-bonding through space interaction between the flanking oxygens of the malaeic anhydride and the delocailsed anti-bonding orbital of the cyclohexadiene. By contrast no such interaction is present in the exo form because of the repositioning of the oxygen atoms relative to the diene unit beneath. This will inevitably have the effect of raising the energy of the transition state for the endo isomer relative to the exo isomer.

However, in opposition works the "secondary orbital effect". ^[3] This is the participation of orbitals not directly involved in bond breaking or making within the transition state and is summarised below:

This effect is large enough to reverse the previously expected transition state energies and cause the endo isomer to have a lower energy than the exo isomer by 0.68 kcal.mol^-1

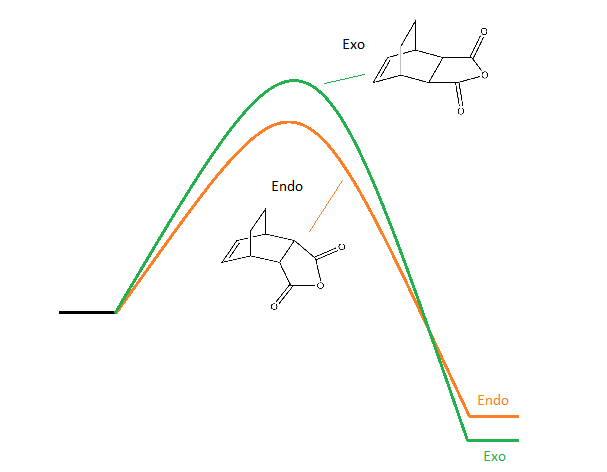
While the endo isomer has the lower energy transition state, it is the exo isomer that has a lower energy product, summarised in the diagram below:

The energy difference in the products is 0.68 kcal.mol^-1 (from IRC calculation).

It can now be understood that the major product of the reaction depends on whether the reaction occurs under kinetic or thermodynamic control: under kinetic control the major product is the endo isomer because of the lower activation energy. The exo isomer could be favoured by placing the reaction instead under thermondynamic control and letting the reaction fully equilibrate.

References

↑ R. Hoffman, W. Stohre, J. Am. Chem. Soc., 1971, 93, 6941
↑ K. N. Houk, Y. Lin, F. K. Brown, J. Am. Chem. Soc, 1986, 108, 554
↑ R. Gleiter, M. C. Bohm, Pure & Appl. Chem., 1983, 55, 237

[1] R. Hoffman, W. Stohre, J. Am. Chem. Soc., 1971, 93, 6941

[2] K. N. Houk, Y. Lin, F. K. Brown, J. Am. Chem. Soc, 1986, 108, 554

[3] R. Gleiter, M. C. Bohm, Pure & Appl. Chem., 1983, 55, 237

[1]

[2]

[3]