Inorganic Computational Report Part 1 - Getting to know Gaussian

Gaussview 5.0 was used in this introduction to computational chemistry to investigate a series of compounds. Optimisations, Frequency and Population analysis was explored and interpretation of these results undertaken.

Energy calculations have an error of approximately 10 kJ.mol^{-1^{(0.0038 atomic units), bond lengths to approximately 0.01 Å, bond angles to 0.1° and dipole moments to 0.01 Debye. Frequency calculations are accurate to around 10%, but are quoted to the nearest integer, as are their intensities by tradition, though their accuracy is substantially less than this.}}

Optimisations

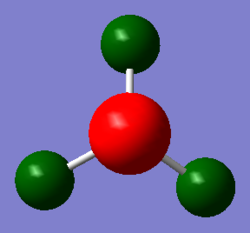
BH₃

A molecule of BH₃ was modeled and optimised using the B3LPY method. Initial optimisation was conducted with the 3-21G basis set, then a second with the higher level 6-31G(d,p) set. The full .log files for the 3-12G and 6-31G(d,p) is provided.

BH₃
File type	.log
Calculation type	FOPT
Method	RB3LYP
Basis Set	3-21G
Energy (au)	-26.4622634
Bond Length (Å)	1.1935
Gradient (au)	0.00020672
Dipole Moment	0.0
Point Group	D3H
Calculation Duration (min)	0.55

 Item               Value     Threshold  Converged?
 Maximum Force            0.000413     0.000450     YES
 RMS     Force            0.000271     0.000300     YES
 Maximum Displacement     0.001610     0.001800     YES
 RMS     Displacement     0.001054     0.001200     YES
 Predicted change in Energy=-1.071764D-06
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  1.1935         -DE/DX =    0.0004              !
 ! R2    R(1,3)                  1.1935         -DE/DX =    0.0004              !
 ! R3    R(1,4)                  1.1935         -DE/DX =    0.0004              !
 ! A1    A(2,1,3)              120.0            -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              120.0            -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              120.0            -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)            180.0            -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------

What is an "optimisation"?

When optimising a molecule, gaussian is effectively scanning the potential energy surface of the molecule for minima. An option on gaussian allows reading of intermediate geometries so you can visualise the iterative process of finding a minimum. Below is a diagram showing the course of the calculation in energy and gradient.

A minimum on the potential energy surface will have a gradient of zero, so the gradient shown here is a measure of how deep into the minimum the optimisation lies.

The choice of basis set is crucial to the quality of the optimisation. Just like a basketball won't fit in a snooker pocket, an unwieldy basis set is unlikely to settle in a genuine energy minimum. Using higher level basis sets is, however, a more computationally challenging task so optimisations are usually run first at a lower level before moving to a more sophisticated basis set.

BH₃ further optimisation

Subsequent optimsation of BH₃ using a higher level basis set, 6-31G(d,p), was undertaken.

BH₃
File type	.log
Calculation type	FOPT
Method	RB3LYP
Basis Set	6-31G(d,p)
Energy (au)	-26.6153236
Bond Length (Å)	1.1923
Gradient (au)	0.00000235
Dipole Moment	0.0
Point Group	D3H
Calculation Duration (min)	0.35

  Item               Value     Threshold  Converged?
 Maximum Force            0.000005     0.000450     YES
 RMS     Force            0.000003     0.000300     YES
 Maximum Displacement     0.000019     0.001800     YES
 RMS     Displacement     0.000012     0.001200     YES
 Predicted change in Energy=-1.304899D-10
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  1.1923         -DE/DX =    0.0                 !
 ! R2    R(1,3)                  1.1923         -DE/DX =    0.0                 !
 ! R3    R(1,4)                  1.1923         -DE/DX =    0.0                 !
 ! A1    A(2,1,3)              120.0            -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              120.0            -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              120.0            -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)            180.0            -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------

TlBr₃

The use of pseudo-potentials was explored in the optimisation of TlBr₃. The calculation was run on the high powered computer (HPC) system, and the result posted in "D-space" - an online repository for permanent storage of crystallographic, computational, and spectrascopic data.

TlBr₃
File type	.log
Calculation type	FOPT
Method	RB3LYP
Basis Set	LANL2DZ
Energy (au)	-91.2181285
Bond Length (Å)	2.6510
Gradient (au)	0.00000090
Dipole Moment	0.0
Point Group	D3H
Calculation Duration (min)	0.15

  Item               Value     Threshold  Converged?
 Maximum Force            0.000002     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000022     0.001800     YES
 RMS     Displacement     0.000014     0.001200     YES
 Predicted change in Energy=-6.084107D-11
 Optimization completed.
    -- Stationary point found.

BBr₃

This basis set, LANL2DZ, differentiates between first row atoms and heavier atoms, running D95V, a medium level basis set on light elements, and Los Alamos ECP (a pseudo potential) on heavier ones.

A molecule of BBr₃ was then modeled using the 6-31G(d,p) basis set for Boron, and LanL2DZ for Bromine by manually altering input file. The optimisation .log file is available, and key results summarised below:

BBr₃
File type	.log
Calculation type	FOPT
Method	RB3LYP
Basis Set	Gen
Energy (au)	-64.4364530
Bond Length (Å)	1.9340
Gradient (au)	0.00000382
Dipole Moment	0.0
Point Group	D3H
Calculation Duration (min)	0.61

 Item               Value     Threshold  Converged?
 Maximum Force            0.000008     0.000450     YES
 RMS     Force            0.000005     0.000300     YES
 Maximum Displacement     0.000036     0.001800     YES
 RMS     Displacement     0.000023     0.001200     YES
 Predicted change in Energy=-4.026780D-10
 Optimization completed.
    -- Stationary point found.

Comparison of Calculated Data

Optimised Bond Lengths
	BH₃	BBr₃	TlBr₃
Bond Length (Å)	1.192	1.934	2.651
Lit. Bond Length (Å)	1.19001 ^[1]	1.893(5) ^[2]	2.52 ^[3]

The trend in bond length observed can rationalised according to the orbitals participating in bonding. In BH₃ the small 1s/2p orbitals overlap effectively forming a strong, compact bond. Altering the ligand in BBr₃, the 2p/4p overlap is substantially worse, leading to the the more diffuse, longer bond computed. Similarly, altering the core atom to Tl, even worse 6p/4p overlap leads to the lengthening presented.

Interestingly, the disparity in calculated and experimental bond length can be seen to increase as more heavier atoms are involved; a reflection of the difficulty involved in computing results for heavy atoms.

Frequency Analysis

Gaussian can also calculate vibrational absorptions, which as well as allowing comparison to experimental results, also indirectly gives feedback on the quality of the optimisations.

Just as energy minima were calculated using the first derivative of the potential energy, the frequencies are calculated by taking the second derivative. A matrix 3N by 3N of force constants is diagonalised to produce 3N "vibrations". It's known that a non-linear molecule exhibits 3N-6 vibrations so some of these vibrations must be incorrect. Within these vibrations are 3 translations and 3 rotations which, ignoring relativity, should be of zero energy. These are quoted as "low frequencies" and deviations from zero indicate non-ideal optimisation. In practice low frequencies of zero are almost never found, but it provides a method to quantify the quality of the optimisations.

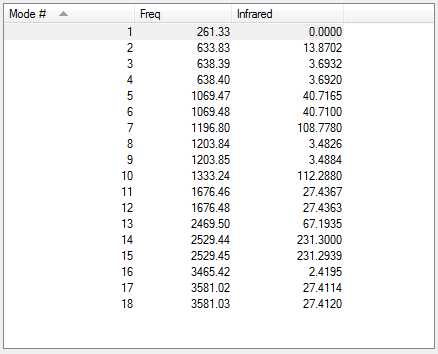
BH₃

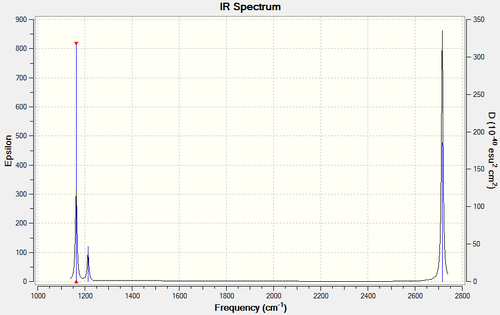
The full frequency analysis for BH₃ is available Below is the calculated IR spectrum and a summary of expected streches.

IR streches for BH₃
No	Form of Vibration	Frequency	Intensity	Symmetry in D_3h point group
1	All 3 hydrogen atoms are uniformly displaced symmetrically in a plane above and below the original molecule. (B-H Wag)	1163	93	A’’
2	2 hydrogen atoms move symmetrically towards and away from one another within the plane of the BH₃ structure while the third hydrogen remains stationary. (B-H Scissor)	1213	14	E’
3	1 hydrogen atom swings from side to side within the plane of the molecule, while the remaining two hydrogen atoms remain relatively stationary, displaced slightly by the recoil of the molecule. (B-H Rock)	1213	14	E’
4	All 3 hydrogen atoms are displaced uniformly, concurrently relative to the central boron within the plane of the molecule. (B-H symmetric stretch)	2582	0	A₁’
5	2 hydrogen atoms are displaced with equal magnitude, but opposing direction relative to boron, while the third hydrogen remains stationary. Maximum displacement for H_A achieved during minimum displacement for H_B. Stretch is within the plane of the molecule (B-H asymmetric stretch)	2715	126	E’
6	2 hydrogen atoms are displaced with equal magnitude, and direction relative to boron, while the third hydrogen atom is displaced both oppositely with respect to boron and to a greater magnitude. (B-H Asymmetric Stretch)	2715	126	E’

  Low frequencies ---   -0.9033   -0.7343   -0.0055    6.7375   12.2491   12.2824
 Low frequencies --- 1163.0003 1213.1853 1213.1880

TlBr₃

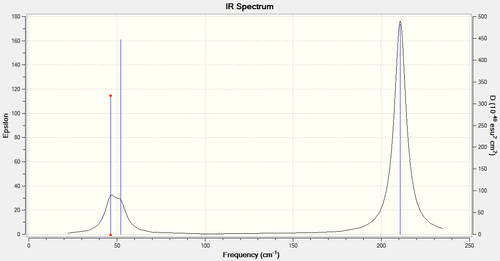
The .log file for the frequency analysis can be accessed via the[D-space link.] A summary of the calculated vibrations along with a predicted IR spectrum are included below.

IR streches for TlBr₃
No	Form of Vibration	Frequency	Intensity	Symmetry in D_3h point group
1	2 bromine atoms move symmetrically towards and away from one another within the plane of the TlBr₃ structure while the third bromine remains stationary. (Tl-Br Scissor)	46	4	E’
2	1 bromine atom swings from side to side within the plane of the molecule, while the remaining two bromine atoms remain relatively stationary, displaced slightly by the recoil of the molecule. (Tl-Br rock)	46	4	E’
3	All 3 bromine atoms are uniformly displaced symmetrically in a plane above and below the original molecule. (Tl-Br Wag)	52	6	A₂’’
4	All 3 bromine atoms are displaced uniformly, concurrently relative to the central thalium within the plane of the molecule. (Tl-Br symmetric stretch)	165	0.00	A₁’
5	2 bromine atoms are displaced with equal magnitude, but opposing direction relative to thalium, while the third bromine remains stationary. Maximum displacement for Br_A achieved during minimum displacement for Br_B. Stretch is within the plane of the molecule (Tl-Br asymmetric stretch)	211	25	E’
6	2 bromine atoms are displaced with equal magnitude, and direction relative to thalium, while the third thalium atom is displaced both oppositely with respect to thalium and to a greater magnitude. (Tl-Br Asymmetric Stretch)	211	25	E’

  Low frequencies ---   -3.4213   -0.0026   -0.0004    0.0015    3.9367    3.9367
 Low frequencies ---   46.4289   46.4292   52.1449

Comparison of Calculated Data

"Missing" peaks

Both BH₃ and TlBr₃ produced 6 computed vibrational frequencies, however the spectra provided show only 2-3 peaks. This can be attributed to a number of factors. Firstly the requirement for a given vibration to be infra-red active is a change in dipole over the course of oscillation. The symmetric sretches involve no net change in dipole hence the zero intensity oberserved for both molecules. Another factor is the presence of degenerate streches - in both molecules there are degenerate bends and streches at identical wavenumbers that cannot be individually resolved. Finally some streches are sufficiently close in energy to cause incomplete resolution of individual peaks leading to the observed spectra.

Analysis

The vibrations of the two molecules share many features, while demonstrating poignent diferences. Most notably the wavenumbers of equivalent absorptions are very different. For example the A₂‘‘ wag is observed at 52.14 cm^-1 for TlBr₃ and 1163.00cm^-1 for BH₃. This huge difference of over 1100 cm^-1 is reflected in other equivalent vibrations and can be rationalised in a number of ways.

Bond strength in the form of the force constant is proportional to the wavenumber according to the equation below, so a higher number correlates to a stronger bond. The 1s/2p orbitals involved in the bonding of BH₃ are small, compact and electron dense allowing for effective σ overlap accounting for the relatively large wavenumber observed. By comparison the large diffuse 4p/6p orbitals largely responsible for the bonding in TlBr₃ overlap poorly, hence the weak bond and low wavenumber observed.

In the same equation frequency can be seen to be inverseley proportional to μ, the reduced mass. There is a sizeable increase in reduced mass moving from BH₃ to TlBr₃ also contributing substantially to the observed disparity.

$\bar{ν} = \frac{1}{2 π c} \sqrt{\frac{k}{μ}}$

$μ = \frac{m_{1} . m_{2}}{m_{1} + m_{2}}$

Where k is the force constant and μ is the reduced mass.

The absorptions for the molecules can broadly be seperated into two groups; one at a lower energy and one at a higher energy. The 3 lowest energy vibrations for both molecules are wags, scissors and rocks. The 3 highest energy vibrations for both molecules are symmetric or asymmetric streches. This pattern is generally observed - bends occur at a lower stretching frequency than stretches. ***These can be considered in terms of their displacement from the central atom. By considering the bond as 2 masses connected by a spring, the follwing expression for a simple harmonic oscillator can be obtained:

$E = \frac{k x^{2}}{2}$

Where x is the displacement from the equilibrium bond length.

According to this model the energy (and thus frequency) of absorption is proportional to the square of displacement from its equilibrium position, x. Bends (wags, scissors, rocks) demand a smaller displacement in the equilibrium bond length, while streches (symmetric, asymmetric) require a significant peturbation. The reduction in the required extention and contraction from the equilibrium length in bends versus streches can explain the disparity in observed wavenumbers for the respective absorptions.

There is also a subtle reordering of the computed vibrations: in BH₃ the lowest energy absorption is a the B-H wag, while for TlBr₃ the analogous wag is at a higher wavenumber than the scissor and rock close in energy to it. This could be because of the notably shorter B-H bond length. The short, compact B-H bond has far less freedom within the plane of the molecule to scissor and rock, but plenty of room above and below the plane of the molecule to wag. By comparison TlBr₃ has far more space in the plane of the molecule owing to the longer, more diffuse Tl-Br bond, which allows the rock and scissor to drop in energy below the wag.

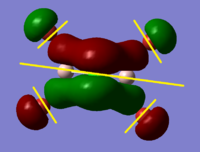
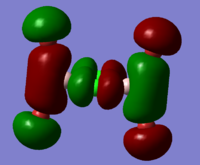
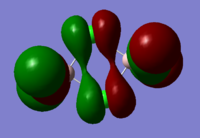
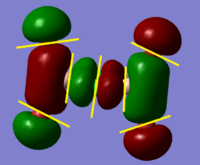
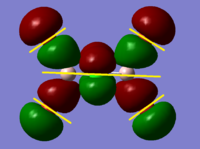
BH₃ Molecular Orbital Calculation

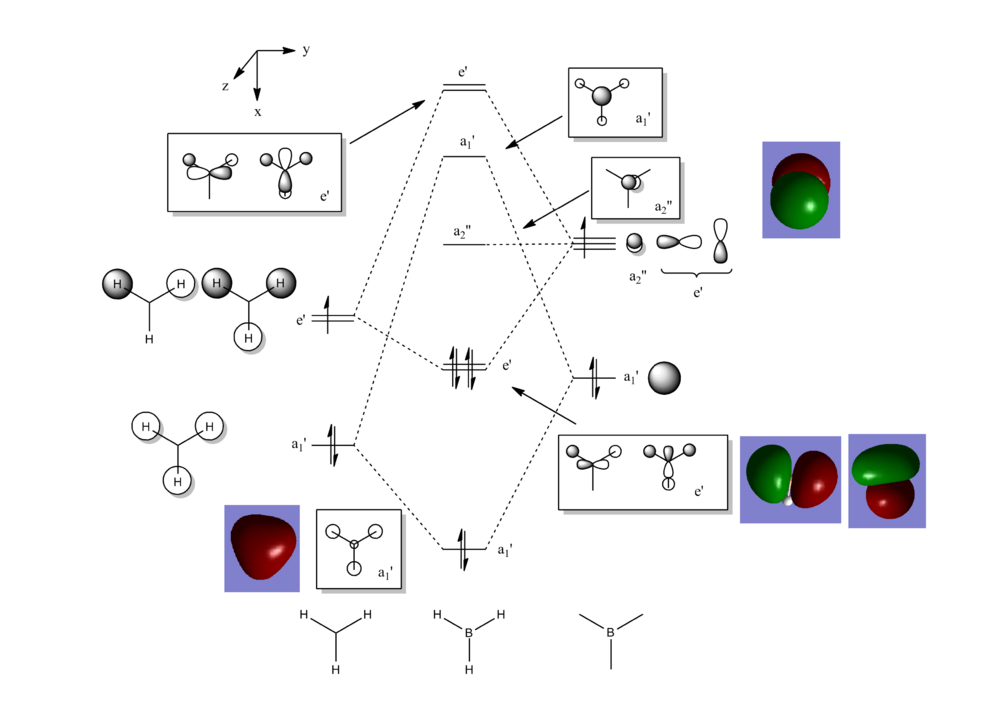
Another very useful feature of gaussian allows calculation of molecular orbitals. D-space link is provided as well as an MO diagram.

The diagram is primarily constructed using the familiar LCAO method for qualitative analysis. The computed, quantitative orbitals are displayed also up to the LUMO level (neglecting core MO). The "real" orbitals show remarkable similarity to those produced using the LCAO method for this relatively simple molecule considering the simplifications employed. The qualitative diagrams fail to accurately depict the dispersion of the MO, however human interpretation of these could easily suggest such a structure with a modicum of theoretical knowledge. Based on this example LCAO would appear to be an effective simplification of molecular orbital theory for small, simple molecules.

Natural Bond Order Analysis of NH₃

Optimisation

NH₃ was optimised using the 6-31G(d,p) basis set. The .log file is available here.

NH₃
File type	.log
Calculation type	FOPT
Method	RB3LYP
Basis Set	6-31G(d,p)
Energy (au)	-56.5577687
Bond Length (Å)	1.0180
Gradient (au)	0.00000185
Dipole Moment	1.847
Point Group	CS
Calculation Duration (min)	0.67

 Item               Value     Threshold  Converged?
 Maximum Force            0.000003     0.000450     YES
 RMS     Force            0.000002     0.000300     YES
 Maximum Displacement     0.000019     0.001800     YES
 RMS     Displacement     0.000011     0.001200     YES
 Predicted change in Energy=-6.948882D-11
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  1.018          -DE/DX =    0.0                 !
 ! R2    R(1,3)                  1.018          -DE/DX =    0.0                 !
 ! R3    R(1,4)                  1.018          -DE/DX =    0.0                 !
 ! A1    A(2,1,3)              105.7453         -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              105.7453         -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              105.7441         -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)           -111.8646         -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------

NH₃ Frequency Analysis

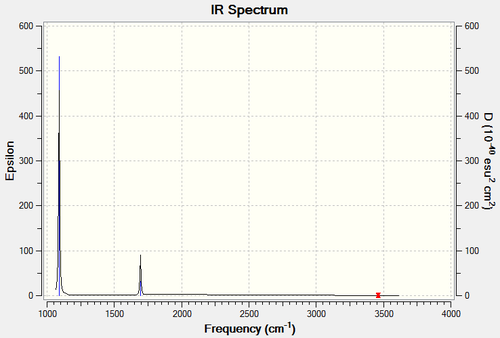
Subsequent frequency analysis is summarised below. The .log file is available, and the computed infra-red spectrum presented.

 Low frequencies ---   -3.3743   -0.0015   -0.0012    0.0004    2.8146    3.9533
 Low frequencies --- 1089.3396 1693.9258 1693.9323

NBO analysis

Full population analysis was carried out on the optimised NH₃ molecule and subsequent NBO analysis probed the bonding in the molecule.(.log file) and .chk file are available.

The image below depicts the charge distribution in a molecule of NH₃ where green shows positive charge and red shows negative charge. (Charge distribution ±1.125)

The natural charge for each atom can also be obtained and is as follows:

N = -1.125 3H = 0.375

NH₃BH₃

NH₃BH₃ was optimised in two steps using the 3-21G then 6-31G(d,p) basis set.

3-21G Optimisation

NH₃BH₃
File type	.log
Calculation type	FOPT
Method	RB3LYP
Basis Set	3-21G
Energy (au)	-82.7666158
Gradient (au)	0.00014023
Dipole Moment	5.840
Point Group	C1
Calculation Duration (min)	0.97

Item               Value     Threshold  Converged?
 Maximum Force            0.000343     0.000450     YES
 RMS     Force            0.000095     0.000300     YES
 Maximum Displacement     0.001724     0.001800     YES
 RMS     Displacement     0.000805     0.001200     YES
 Predicted change in Energy=-8.543345D-07
 Optimization completed.
    -- Stationary point found.

6-31G(d,p) Optimisation

NH₃BH₃
File type	.log
Calculation type	FOPT
Method	RB3LYP
Basis Set	6-31G(d,p)
Energy (au)	-83.2246867
Gradient (au)	0.00019726
Dipole Moment	5.571
Point Group	C1
Calculation Duration (min)	0.63

  Item               Value     Threshold  Converged?
 Maximum Force            0.000270     0.000450     YES
 RMS     Force            0.000149     0.000300     YES
 Maximum Displacement     0.001636     0.001800     YES
 RMS     Displacement     0.000775     0.001200     YES
 Predicted change in Energy=-1.697922D-06
 Optimization completed.
    -- Stationary point found.

Frequency Analysis

Subsequent vibrational analysis of the optimised file yielded the spectrum shown below. The .log file is attached, and low frequencies recorded.

 Low frequencies ---  -14.5112   -0.0003    0.0005    0.0010    3.7286    4.1571
 Low frequencies ---  261.5551  633.8271  638.3935

Bond Energy Calculations

The energies of the molecules are summarised in the table below, all expressed in atomic units (au)

Bond Energy Summary
Molecule	Energy (au)
BH₃	-26.6153236
NH₃	-56.5577687
NH₃BH₃	-83.2246867

The bond association energy in forming this dative covelant bond can be calculated using E(NH₃BH₃) - [E(NH₃) + E(BH₃)] = -0.0515944 au

-0.0515944 au x 2625.5 = -135.46 kJ.mol^-1

The negative value shows the adduct is, enthalpicly, more stable than the monomer constituents.

The literature value is ***

Inorganic Computational Report 2 - Lewis Acids and Bases Mini-Project

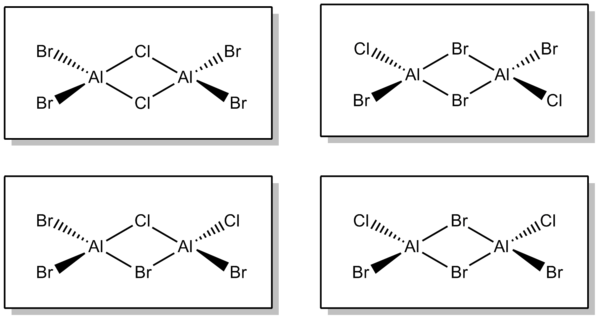
BH₃ is an electron deficient species and will dimerise to form B₂H₆ bridging through hydrogen atoms. Analagous lewis acids also tend to form oligomers, as will be explored in this mini project. The energetics surrounding the dimerisation of AlClBr₂ will be investigated, and subsequent analysis on the oligomeric species undertaken. (This is different from the molecule suggested in lab script due to a reading error, but Dr. Hunt has allowed me to use the analysis I conducted on these species). There are four different isomers of this compound summarised below:

Optimisations

All four isomers will be optimised fully using the 6-31G(d,p) basis set for aluminium and chlorine, and the LanL2DZ method for bromine, carried out by manually altering the gaussian input file. Typical input file modification is demonstrated below:

 Al 0
6-31G(d,p)
****
Cl 0
6-31G(d,p)
****
Br 0
LanL2DZ

Br 0
LanL2DZ

Tight convergence criteria were enforced in order to produce the most accurate prediction possible.

Incorrect point groups were assigned by gaussian during optimisations, so the correct symmetry is given in the summaries in square brackets. This symmetry was the enforced for the subsequent frequency analysis.

Isomer 1 - (AlBr₂(μ-Cl))₂

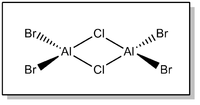Full .log file available at D-space repository

(AlBr₂(μ-Cl))₂
File type	.log
Calculation type	FOPT
Method	RB3LYP
Basis Set	GEN
Energy (au)	-1458.3511699
Gradient (au)	0.00000045
Dipole Moment	0.000
Point Group	C1 [D2h]
Calculation Duration (min)	5.33

  Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000015     YES
 RMS     Force            0.000000     0.000010     YES
 Maximum Displacement     0.000024     0.000060     YES
 RMS     Displacement     0.000008     0.000040     YES
 Predicted change in Energy=-2.649685D-11
 Optimization completed.
    -- Stationary point found.

Isomer 2 - cis-ClBrAl(μ-Br)₂AlBrCl

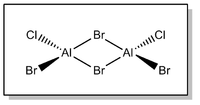Full .log file available at D-space repository

cis-ClBrAl(μ-Br)₂AlBrCl
File type	.log
Calculation type	FOPT
Method	RB3LYP
Basis Set	GEN
Energy (au)	-1458.3412190
Gradient (au)	0.00000004
Dipole Moment	0.177
Point Group	C1 [C_2v]
Calculation Duration (min)	8.11

 Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000015     YES
 RMS     Force            0.000000     0.000010     YES
 Maximum Displacement     0.000005     0.000060     YES
 RMS     Displacement     0.000002     0.000040     YES
 Predicted change in Energy=-1.099844D-13
 Optimization completed.
    -- Stationary point found.

Isomer 3 - trans-ClBrAl(μ-Br)₂AlBrCl

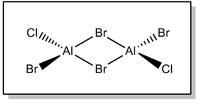Full .log file available on D-space

trans-ClBrAl(μ-Br)₂AlBrCl
File type	.log
Calculation type	FOPT
Method	RB3LYP
Basis Set	GEN
Energy (au)	-1458.3412426
Gradient (au)	0.00000021
Dipole Moment	0.0000
Point Group	C1 [C_2h]
Calculation Duration (min)	7.25

Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000015     YES
 RMS     Force            0.000000     0.000010     YES
 Maximum Displacement     0.000004     0.000060     YES
 RMS     Displacement     0.000001     0.000040     YES
 Predicted change in Energy=-1.307817D-12
 Optimization completed.
    -- Stationary point found.

Isomer 4 - ClBrAl(μ-Cl)(μ-Br)AlBrCl

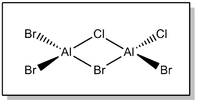The full .log file is available on D-space

ClBrAl(μ-Cl)(μ-Br)AlBrCl
File type	.log
Calculation type	FOPT
Method	RB3LYP
Basis Set	GEN
Energy (au)	-1458.3459916
Gradient (au)	0.00000258
Dipole Moment	0.120
Point Group	C1
Calculation Duration (min)	2.77

 Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000015     YES
 RMS     Force            0.000001     0.000010     YES
 Maximum Displacement     0.000039     0.000060     YES
 RMS     Displacement     0.000019     0.000040     YES
 Predicted change in Energy=-2.897124D-10
 Optimization completed.
    -- Stationary point found.

Monomer - AlClBr₂

Full .log file available in D-space

AlClBr₂
File type	.log
Calculation type	FOPT
Method	RB3LYP
Basis Set	GEN
Energy (au)	-729.1582437
Gradient (au)	0.00000160
Dipole Moment	0.104
Point Group	C2V
Calculation Duration (min)	1.57

 Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000015     YES
 RMS     Force            0.000002     0.000010     YES
 Maximum Displacement     0.000017     0.000060     YES
 RMS     Displacement     0.000007     0.000040     YES
 Predicted change in Energy=-4.998618D-11
 Optimization completed.
    -- Stationary point found.

Relative Energies

Because all calculations were conducted under identical conditions relative energies can be calculated. By comparing the calculated energies of the dimers the most stable species can be identified.

	AlBr₂(μ-Cl))₂	cis-ClBrAl(μ-Br)₂AlBrCl	trans-ClBrAl(μ-Br)₂AlBrCl	ClBrAl(μ-Cl)(μ-Br)AlBrCl	AlClBr₂
Absolute Energy (au)	-1458.3511699	-1458.3412190	-1458.3412426	-1458.3459916	-729.1582437
Relative Energy (kJ.mol^-1)	0	26.13	26.06	13.60	---

It can be seen from the data above that the most stable species are those with the most chloride-bridges; each one stabilises the molecule by approximately 13 kJ.mol^-1 over an equivalent bromide. This can be rationalised in terms of the electron density of the constituent orbitals; the diffuse 3p orbital primarilly used by bromine in bond formation will overlap more poorly with the aluminium 2p orbital than the chlorine 2p orbital. This ineffective overlap will lead to a weaker bond, and confer the increase in energy observed.

The dissociation energy of the dimers into the monomers can also be calculated in an analogous fasion to ammonia-borane above: E(AlBr₂(μ-Cl))₂) - 2(E(AlClBr₂)) = -0.0346825 au =-91.06 kJ.mol^-1

The negative dissociation energy corresponds to the monomer being unstable with respect to the dimer just as the lewis acids considered earlier behave.

Frequency Analysis

Frequency analysis was conducted on all the species identified and optimised above to confirm the structures as genuine minima, and to conduct subsequent analysis on the results. The intensities are quoted to 2 decimal places in order to give the reader information on the number of IR active modes, however it should be noted that measurements are far less accurate than this and are generally reported to the nearest integer.

Isomer 1 - Br₂Al(μ-Cl)₂AlBr₂

The full .log file for the frequency analysis is available on D-space.

 Low frequencies ---   -1.7095   -0.7915   -0.0020   -0.0015   -0.0008    1.9968
 Low frequencies ---   15.3634   38.7845   59.6734

The simulated spectrum along with a summary of the observed stretches are given below:

IR streches for Br₂Al(μ-Cl)₂AlBr₂
No	Form of Vibration	Frequency	Intensity	Symmetry in D_2h point group
1	Terminal Al-Br₂ rock symmetrically causing a recoil in the Al-Cl-Al unit that looks like a small wag	15	0.34	B_2u
2	Terminal Al-Br bonds twist. Across the molecule the two AlBr₂ groups can be seen to twist asymmetrically.	39	0.00	A_u
3	Terminal Al-Br bonds scissor with a small concomitant elongation of the Al-Cl bridging bonds in recoil.	60	0.00	A_g
4	Bridging Al-Cl-Al bonds twist.	83	0.00	B_1g
5	Terminal Br-Al-Br bond scissor asymmetric across the molecule.	96	8.29	B_3u
6	Terminal bromine atoms move symmetrically above and below the plane of the Br-Al-Br bonds (Al-Br wag)	101	6.68	B_1u
7	Bridging Cl-Al-Cl bond twist	105	0.00	B_3g
8	Terminal Br-Al-Br wag asymmetric across the molecule	145	0.00	B_2g
9	Bridging chlorine atoms bend above and below the plane of the Al-Cl-Al unit (Al-Cl-Al wag)	148	4.73	B_2u
10	Bridging Al-Cl-Al bond scissoring with small concomitant recoil in the Al-Br terminal unit.	158	0.00	A_g
11	Bridging Cl-Al-Cl symmetric stretch, asymmetric with respect to the other Al atom. Max Cl-Al_a-Cl bond length at min Cl-Al_b-Cl bond length. Concomitant symmetric Al-Br stretch, again asymmetric across the molecule, possibly in recoil.	243	5.98	B_3u
12	Bridging Cl-Al-Cl asymmetric stretch	260	0.00	B_2g
13	Bridging Al-Cl bond stretch with concomitant Cl-Al-Cl scissoring	291	0.00	A_g
14	Bridging Cl-Al-Cl symmetric stretch, asymmetric across the central unit.	400	462.92	B_3u
15	Bridging Cl-Al-Cl asymmetric stretch, symmetric across the central unit.	407	138.68	B_1u
16	Bridging Cl-Al-Cl symmetric stretch, symmetric across the central unit.	445	0.00	A_g
17	Terminal Br-Al-Br asymmetric stretch, asymmetric across the molecule	491	0.00	B_1g
18	Terminal Br-Al-Br asymmetric stretch, symmetric across the molecule	502	288.63	B_2u

Isomer 2 - cis-ClBrAl(μ-Br)2AlBrCl

The full .log file is available on D-Space

Low frequencies ---   -0.7759    0.0008    0.0015    0.0017    1.2915    1.4902
 Low frequencies ---   12.9489   50.1427   71.1759

The simulated spectrum along with a summary of the vibrations is given below:

IR streches for cis-ClBrAl(μ-Br)₂AlBrCl
No	Form of Vibration	Frequency	Intensity	Symmetry in C_2v point group
1	Terminal group rock (Cl-Al-Br rock), with concomitant bridging bromide distortion.	13	0.23	A₁
2	Terminal group twist, asymmetric across the molecule.	50	0.00	A₂
3	Terminal group scissor, with small concomitant bridging-wag	71.1	0.01	A₁
4	Bridging Br-Al-Br twist with concomitant terminal bromide rock. Stationary terminal chloride.	73	0.46	B₁
5	Bridging Al-Br-Al twist with concomitant recoil in terminal groups	90	0.31	B₂
6	Terminal Al-Cl wag, symmetric across the molecule	99	3.19	B₁
7	Terminal Al-Cl rock, asymmetric across the molecule	110	6.92	B₂
8	Bridging Al-Br-Al wag with small concomitant terminal group rock	123	4.78	A₁
9	Terminal Cl-Al-Br group wag, asymmetric across the molecule	125	0.00	A₂
10	Bridging Al-Br-Al scissor	152	0.03	A₁
11	Bridging Br-Al-Br asymmetric stretch, asymmetric across the molecule	193	0.00	A₂
12	Bridging Br-Al-Br symmetric stretch, asymmetric across the molecule	216	56.85	B₂
13	Bridging Br-Al-Br symmetric stretch, symmetric across the molecule	219	0.93	A₁
14	Bridging Br-Al-Br asymmetric stretch, symmetric across the molecule	334	147.39	B₁
15	Bridging Br-Al-Br symmetric stretch, asymmetric across the molecule with a concomitant symmetric Br-Al-Cl terminal group stretch, asymmetric across the molecule	397	346.87	B₂
16	Bridging Br-Al-Br symmetric stretch, symmetric across the molecule, with concomitant symmetric Br-Al-Cl terminal group stretch, symmetric across the molecule	427	29.07	A₁
17	Terminal Br-Al-Cl asymmetric stretch, asymmetric across the molecule	569	31.27	B₂
18	Terminal Br-Al-Cl asymmetric stretch, symmetric across the molecule	579	281.65	A₁

Isomer 3 - trans-ClBrAl(μ-Br)₂AlBrCl

The full .log file for the frequency analysis is available on D-Space

 Low frequencies ---   -1.5133   -0.0007   -0.0003    0.0006    0.3376    0.9592
 Low frequencies ---   13.1602   47.9000   67.3966

The simulated spectrum along with a summary of the frequencies are given below:

IR streches for trans-ClBrAl(μ-Br)₂AlBrCl
No	Form of Vibration	Frequency	Intensity	Symmetry in C_2v point group
1	Terminal Cl-Al-Br rock with concomitant Al-Br-Al wag	13	0.24	B_u
2	Terminal Cl-Al-Br twist asymmetric across the molecule	48	0.09	A_u
3	Terminal Cl-Al-Br scissor with minimal Al-Cl motion, symmetric across the molecule. Concomitant minor Br-Al-Br bridging group scissor	67	0.00	A_g
4	Bridging Br-Al-Br twist with concomitant Cl-Al-Br terminal group twist, possibly as recoil	76.4	0.00	B_g
5	Terminal Cl-Al-Br wag, symmetric across the molecule with major contribution from Cl, minor Br movement.	97	3.57	A_u
6	Terminal Al-Cl rock, symmetric across the molecule.	98	0.00	A_g
7	Terminal Cl-Al-Br scissor, asymmetric across the molecule	105	5.23	B_u
8	Terminal Al-Cl rock, symmetric across the molecule with concomitant bridging Al-Br-Al wag. Stationary terminal Br.	123	6.94	B_u
9	Terminal Br-Al-Cl wag, asymmetric across the molecule	125	0.00	B_g
10	Bridging Br-Al-Br scissor, symmetric across the molecule, with concomitant Cl-Al-Br scissor possibly in recoil	151	0.00	A_g
11	Bridging Br-Al-Br asymmetric stretch, asymmetric across the molecule. Stationary terminal units.	193	0.00	B_g
12	Bridging Br-Al-Br symmetric stretch, asymmetric across the molecule with concomitant terminal Cl-Al-Br scissor possibly as recoil	216	57.81	B_u
13	Bridging Br-Al-Br symmetric stretch, symmetric across the molecule with concomitant terminal Cl-Al-Br scissor	218	0.00	A_g
14	Bridging Br-Al-Br asymmetric stretch, asymmetric across the molecule. Terminal unit stationary	334	147.40	A_u
15	Bridging Br-Al-Br symmetric stretch, asymmetric across the molecule with concomitant terminal Cl-Al-Br symmetric stretch, asymmetric across the molecule	398	374.31	B_u
16	Terminal Cl-Al-Br symmetric stretch, symmetric across the molecule with concomitant bridging Al-Br-Al scissor, symmetric across the bridging unit	462	0.00	A_g
17	Terminal Cl-Al-Br asymmetric stretch, asymmetric across the molecule with concomitant bridging Al-Br-Al twist. Cl-Al contribution to asymmetric stretch notably larger than Br-Al.	571	0.00	A_g
18	Terminal Cl-Al-Br asymmetric stretch, symmetric across the molecule with concomitant bridging A;-Br-Al wag. Cl-Al contribution to asymmetric stretch notably larger than Br-Al.	576	313.89	B_u

Isomer 4 - ClBrAl(μ-Cl)(μ-Br)AlBrCl

The full .log file for the frequency analysis is available on D-Space

 Low frequencies ---   -0.0028   -0.0024   -0.0018    0.8980    1.4718    1.5432
 Low frequencies ---   14.1416   44.0763   64.0780

The simulated sprectrum as well as a summary of the computed absorptions are shown below. Due to the point group of the molecule being C₁, the symmetry of the vibrations will not be included. Some computed vibrations contain movements on a single side of the plane created by the central bridging section. By tracing the bonds from terminal Br-Al-Al-terminal Br one unit can be seen, while tracing the other terminal Br-Al-Al-terminal Cl the other unit can be seen. In certain vibrations these are observed to move independently and will be referred to herein as "bromine unit" and "chlorine unit" respectively. The bridging bonds can also be split into those on the side of the molecule that bears 2 terminal bromines (bromine side bonds) and 1 terminal bromine and 1 terminal chlorine (chlorine side bonds).

IR streches for ClBrAl(μ-Cl)(μ-Br)AlBrCl
No	Form of Vibration	Frequency	Intensity
1	Bridging group wag (-Al-Cl-Al-Br-)	14	0.29
2	Terminal group twist, asymmetric across the molecule	44	0.02
3	Terminal group scissor, symmetric across the molecule with notably less sscission in the Cl-Al-Br terminal unit	64	0.14
4	Bridging Cl-Al-Br twist with concomitant rock of Al-Br bond. Chlorine remains stationary.	82	0.65
5	Bromine unit rock while chlorine unit remains stationary	88	0.53
6	Terminal group wag, symmetric across the molecule. Cl-Al-Br bromine relatively stationary.	94.6	3.81
7	Terminal group scissor, symmetric across the molecule. Large contribution from Al-Cl bond.	104	6.03
8	Terminal group wag, asymmetric across the molecule.	135	2.74
9	Bridging group wag, symmetric across the molecule. Very large contribution from Al-Cl-Al bond	141	5.03
10	Bridging group scissor, with concomitant terminal group scissor. Large contribution from Al-Cl-Al bond	163	0.39
11	Bridging group asymmetric stretch, asymmetric across the molecule, with larger contribution from Al-Br-Al.	200	16.69
12	Bromine side bonds: Symmetric stretch - larger contributions from Al-Cl bond. Chlorine side bonds: Br-Al stretch with almost no Cl-Al stretch. Br-Al-Br terminal group small symmetric stretch. Br-Al-Cl terminal group stationary.	273	6.76
13	Bridging Al-Cl asymmetric stretch	265	12.58
14	Bridging Br-Al-Cl asymmetric stretch, symmetric across the molecule. Terminal units stationary.	374	148.43
15	Bromine side bridging Br-Al-Cl symmetric stretch, concomitant with terminal Br-Al-Br symmetric stretch. Chlorine side Al-Br stretch, asymmetric with respect to bromise side bridging symmetric stretch. Very little bridging Al-Cl stretch. Br-Al-Cl terminal symmetric stretch with minimal Al-Cl participation.	395	374.40
16	Bridging Br-Al-Cl symmetric stretch, symmetric across the molecule, with concomitant terminal unit symmetric stretch (smaller contribution from Al-Cl).	438	32.49
17	Terminal Br-Al-Br asymmetric stretch. All other atoms relatively stationary, including terminal Br-Al-Cl.	494	131.69
18	Terminal Br-Al-Cl asymmetric stretch with larger contribution from Al-Cl bond. All other atoms relatively stationary.	576	169.39

In-depth Frequency Analysis

The reasons outlined for variation in computed absorptions for equivalent stretches in part 1 also play a major role in this scenario. The double-bridging wag (Isomer 1 [no 9], Isomers 2 and 3 [no 8]) occur at 148 and 123 cm^-1 respectively, which I believe can be attributed largely to the decrease in reduced mass observed moving from isomer 1 (Br) to isomer 2 (Cl). There are, however, other factors that contribute significantly to the calculated vibrations.

In general it is observed that terminal chlorine stretches occur at a greater wavenumber than the bridging chlorine stretches. For example the asymmetric terminal Br-Al-Cl stretch (Isomer 2, 3 and 4 [no 18]) occurs around 575 cm^-1. The highest energy stretch of the bridging chloride (Isomers 1 and 4 [no 16]) occurs at around 440 cm^-1. This can be rationalised by invoking knowledge of the bonding mechanism in these lewis acidic species. Bonding through bridging hydrides and halides occurs via 3-centre-2-electron bonds. This reduces the bond order of the bridged system relative to the classic 2c-2e bond, and accordingly the force constant for the bond is reduced. It can be seen in the equation earlier that the frequency of oscillation is proportional to the square root of the force constant and so as expected, the observed frequency is reduced.

The vibrations of isomer 4 are far more convoluted and difficult to assign precisely because the loss of symmetry has a profound effect on the molecule. The contributions of different bonds are difficult to quantify visually, and accordingly the assignment could be erroneous. This loss of symmetry does, however, have a huge impact on the number of IR active modes, a summary table for which is below.

Number of IR-Active Modes
Isomer	Number of Bridging Chlorines	Symmetry	Number of IR-Active Modes
1 - Br₂Al(μ-Cl)₂AlBr₂	2	D_2h	8
2 - cis-ClBrAl(μ-Br)₂AlBrCl	0	C_2v	15
3 - trans-ClBrAl(μ-Br)₂AlBrCl	0	C_2h	9
4 - Br₂Al(μ-Br)(μ-Cl)AlBrCl	1	C₁	18

It can be seen that as symmetry is broken from D_2h to C₁ there is an increase in IR-active modes. This follows logically from the necessary requirement in an IR-active stretch of a change in dipole moment. A highly symmetric molecule will have planes of symmetry such that a vibration on one side of the molecule may be cancelled out by a stretch opposite in direction but equal in magnitude on the other side of the molecule.

Some particularly interesting aspects of the computed vibrations stand out as worth discussing. Vibration [no 10] present in all isomers as a scissior within the bridging unit whatever the constituent atoms may be shows an interesting relationship between frequency and atomic makeup. Given the trends seen up until this point with regards to reduced mass and frequency, one might expect that moving from Al₂Br₂ to Al₂ClBr through to Al₂Cl₂ there would be an increase in the absorption frequency, however this is not what is observed. The Al₂Br₂ species has absorption at around 152 cm^-1 for the -cis and -trans molecules and the Al₂Cl₂ at 158 cm^-1, while the Al₂ClBr species has absorption at 163 cm^-1. I am unaware of the reason for this disparity, however I would suggest it is due to the small 4-membered ring system and the strain this exerts, particularly in reference to the varying degrees of scissioring motion desired by the Al-Br-Al bond and Al-Cl-Al bond respectively. The marked lack of flexibility in the system and conflicting requirements may raise the overall energy of the vibration giving the result observed. This line of logic intruiged me, and investigating further I can find other examples to tentatively support my idea. Isomer 1 [no 12] and isomer 4 [no 13] show bridging Al-Cl-Al asymmetric stretches. One might tentatively expect that isomer 4, with a more electronegative terminal chlorine, would withdraw electron density from the aluminium rendering the 3c-2e bond weaker leading to a lower wavenumber. In fact the absorptions are isomer 1 - 260 cm^-1, isomer 4 - 265 cm^-1. When visualising these vibrations isomer 4 with a static bromine atom in the bridging system looks particularly strained when compared with isomer 1, so perhaps the Al-Br bonds total non-participation in the stretch produces the unexpectedly high value by introducing strain into the compact ring system as before. Isomer 1 [no 15] Isomers 2, 3, 4 [no 14] is an as X-Al-X asymmetric stretch across the entire bridging unit and shows absorptions at: Isomers 2, 3 - 334 cm^-1; isomer 4 - 378 cm^-1; isomer 1 - 407 cm^-1. This is more in line with the expected pattern according to reduced mass. Following the logic outlined above, I believe this could be because the asymmetric stretches across the entire bridging unit are actually complementary in isomer 4 so the strain experienced in the other stretches by either non-participation of one atom or differing requirements prohibited by geometry, is no longer present. This is, of course, highly speculative and only explored for interest!

Population Analysis of Br₂Al(μ-Cl)₂AlBr₂

A full population analysis was conducted on the lowest energy isomer using the same method as before, and files are available on D-Space.

Selected non-core MOs were selected for more detailed investigation shown below. Non-core MOs are those pertaining to the valence electrons of the species. Al has 3 valence electrons, Br 7 and Cl 7 so the molecule contains 48 valence electrons, which can be distributed between 24 orbitals. Not considered are the 152 core electrons constituting the 78 core MOs. Herein the orbitals are taken from 79 = 1 for simplicity's sake.

Selected Molecular Orbitals of Br₂Al(μ-Cl)₂AlBr₂
Number	Diagram	Description	Diagram of Nodes
10		Highly delocalised strongly bonding orbital with strong bonding through space interactions throughout the Al-Cl bridging unit, encompassing the Al-Br bond. Nodal plane throughout the centre of the molecule incedent with the Al-Cl-Al bridging bonds. 4 nodal points flank the terminal bromine atoms.
14		Moderately delocalised, bonding orbital. Weak bonding through space interaction traverses the bridging unit delocalised across the two bridging chlorine atoms. Strong bonding interaction between aluminium and terminal bromines produces moderately delocalised orbitals on either side of the central unit. Moderate antibonding interaction between the bridging orbital and the terminal orbital. Nodal plane perpendicular to the bridging unit through both chlorine atoms. Nodal points between bridging orbital and Br-Al-Br, and through bromine atoms.
16		Highly localised, very strongly antibonding orbital. Very strong antibonding through space interaction between bridging chlorine and aluminium. Bonding interaction between Al and Br. Smaller orbital contribution from Cl compared to Br.
17		Through space bonding interaction encompasses the terminal unit perpendicular to the Al-Cl bridge producing a delocalised orbital with nodal planes incedent with the Al-Br bonds. Very small orbital contribution from the chlorine atoms, which display antibonding through space interactions both with each other the terminal orbitals. Nodal points found at all Al-Cl bonds as well as through bromine atoms. Possibly slightly bonding.
21		Non-bonding orbital showing localised p orbitals perpendicular to the Br-Al-Br plane, residing on bromine atoms. No through space, antibonding or bonding interactions. Nodal points located on the bromine atoms.

References

↑ K. Kawaguchi, J. Chem. Phys., 1992, 96, 3411,
↑ S. Konaka, T. Ito, Y. Morino, Bull. Chem. Soc. Jpn.,, 1966, 39, 1146, .
↑ J. Blixt, J. Glaser, J. Mink, I. Persson, P. Persson, M. Sandstrom, J. Am. Chem. Soc., 1995, 117, 5089 - 5104

[1] K. Kawaguchi, J. Chem. Phys., 1992, 96, 3411,

[2] S. Konaka, T. Ito, Y. Morino, Bull. Chem. Soc. Jpn.,, 1966, 39, 1146, .

[3] J. Blixt, J. Glaser, J. Mink, I. Persson, P. Persson, M. Sandstrom, J. Am. Chem. Soc., 1995, 117, 5089 - 5104

[1]

[2]

[3]

Inorganic Computational Report Part 1 - Getting to know Gaussian

Optimisations

BH3

What is an "optimisation"?

BH3 further optimisation

TlBr3

BBr3

Comparison of Calculated Data

Frequency Analysis

BH3

TlBr3

Comparison of Calculated Data

"Missing" peaks

Analysis

BH3 Molecular Orbital Calculation

Natural Bond Order Analysis of NH3

Optimisation

NH3 Frequency Analysis

NBO analysis

NH3BH3

3-21G Optimisation

6-31G(d,p) Optimisation

Frequency Analysis

Bond Energy Calculations

Inorganic Computational Report 2 - Lewis Acids and Bases Mini-Project

Optimisations

Isomer 1 - (AlBr2(μ-Cl))2

Isomer 2 - cis-ClBrAl(μ-Br)2AlBrCl

Isomer 3 - trans-ClBrAl(μ-Br)2AlBrCl

Isomer 4 - ClBrAl(μ-Cl)(μ-Br)AlBrCl

Monomer - AlClBr2

Relative Energies

Frequency Analysis

Isomer 1 - Br2Al(μ-Cl)2AlBr2

Isomer 2 - cis-ClBrAl(μ-Br)2AlBrCl

Isomer 3 - trans-ClBrAl(μ-Br)2AlBrCl

Isomer 4 - ClBrAl(μ-Cl)(μ-Br)AlBrCl

In-depth Frequency Analysis

Population Analysis of Br2Al(μ-Cl)2AlBr2

References

BH₃

BH₃ further optimisation

TlBr₃

BBr₃

BH₃

TlBr₃

BH₃ Molecular Orbital Calculation

Natural Bond Order Analysis of NH₃

NH₃ Frequency Analysis

NH₃BH₃

Isomer 1 - (AlBr₂(μ-Cl))₂

Isomer 2 - cis-ClBrAl(μ-Br)₂AlBrCl

Isomer 3 - trans-ClBrAl(μ-Br)₂AlBrCl

Monomer - AlClBr₂

Isomer 1 - Br₂Al(μ-Cl)₂AlBr₂

Isomer 3 - trans-ClBrAl(μ-Br)₂AlBrCl

Population Analysis of Br₂Al(μ-Cl)₂AlBr₂