Rep:Mod:dd1991 physical

Daniel Davies, Year 3 Computational Labs, Physical Module

Introduction

This module was conducted to gain an understanding of transition state modelling in Gaussian. The transition state of a reaction lies at a maximum saddle point along the potential energy surface of the reaction . Experimentally it is not possible to observe these passing states, even with spectroscopic methods, due to there essentially instantaneous lifetimes.

Understanding the transition state of reaction is valuable in assigning reaction mechanisms and also in explain observed kinetics of a certain reaction. Computer modelling allows for for the geometric and energetic parameters of transition states to be predicted. This module will look at locating the transition states in two classes of reactions. The first being Clasion Rearrangements and the second being Diels-Alder reactions.

All energies are quoted in Hartree au units unless otherwise stated (1 Hartree au = 2625.50 kJmol-1 = 627.51 kcalmol). A calculation is considered successful if the RMS gradient value is less than 0.0001

The Cope Rearrangement

The Cope rearrangement is a pericyclic reaction that can be classed as a [3+3] sigmatropic rearrangement Pericyclic reactions are interesting cases to study due to the concerted nature of their reactions that pass through one transition state without forming any intermediates in the process. The reaction of 1,5-hexadiene can be said to go through either one of two transition states, boat or chair.

Cope Rearrangement of 1,5-hexadiene

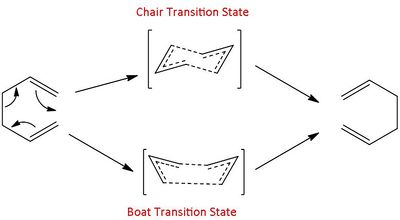
In this section the lowest energy conformers of 1,5-hexadiene were isolated using Gaussian optimisation calculations before attempting to locate the boat and chair transition states.

Optimisation of 1,5-hexadiene conformers

In this section a series of conformers of the 1,5-hexadiene molecule was optimised to investigate which one is most energetically stable. In theory 1,5-hexadiene has 27 conformations it can adopt. Due to symmetry of the molecule and entiomerism of the conformers only 10 are energetically distinguishable. If simply taking into account just the steric interactions in the molecule it would be expected that an anti-peri planar (app) conformation would be most stable due to minimisation of Pauli repulsion. However these interactions are not the only interactions present. Orbital overlap and van der Waals interactions are key in conformational analysis and leads to what is known as the "gauche effect", where a gauche conformer is more stable than an app one.

Each one of the 10 distinguishable conformers of 1,5-hexadiene was constructed using Gaussview and then optimised using a Hatree-Fock method with a 3-21G basis. Details of these calculations and results are given in the following table.

Calculation Information	Anti 1	Anti 2	Anti 3	Anti 4
J-Mol
File Type	.log	.log	.log	.log
Calculation type	FOPT	FOPT	FOPT	FOPT
Calculation Method	RHF	RHF	RHF	RHF
Basis Set	3-21G	3-21G	3-21G	3-21G
Final Energy	-231.69260	-231.69254	-231.68907	-231.69097
Gradient	0.0000130	0.0000190	0.0000419	0.0000077
Dipole Moment	0.20215D	0D	0D	0.2955
Point Group	c1	Ci	C2h	C1
Calculation Running Time	1 min 4 secs	43.9secs	18.8 secs	40.5 secs
D-space	anti 1	anti 2	anti 3	anti4

Calculation Information	gauche 1	gauche 2	gauche 3	gauche 4	gauche 5	gauche 6
J-Mol
File Type	.log	.log	.log	.log	.log	.log
Calculation type	FOPT	FOPT	FOPT	FOPT	FOPT	FOPT
Calculation Method	RHF	RHF	RHF	RHF	RHF	RHF
Basis Set	3-21G	3-21G	3-21G	3-21G	3-21G	3-21G
Final Energy	-231.68772	-231.69167	-231.69266	-231.69153	-231.68962	-231.68916
Gradient	0.0000133	0.0000033	0.0000118	0.0000204	0.0000127	0.0000067
Dipole Moment	0.4557D	0.3804D	0.3405D	0.1281D	0.4438	0.5361D
Point Group	C2	C2	C1	C2	C1	C1
Calculation Running Time	49.8 secs	1 mins 15.2secs	48.3 secs	38.4 secs	1 mins 52.7 secs	2 mins 17.6 secs
D-space	gauche 1	gauche 2	gauche 3	gauche 4	gauche 5	gauche 6

The energies that were calculated above agree with those provided in "Appendix 1" of the instructions. The gauche 3 appears to be lowest energy conformer. The reason for this conformer being more stable than the app is found in the literature and can be attributed to a favourable overlap of the two pi orbitals from the two double bonds. This orbital interaction is clearly seen in the HOMO j-mol visualisation presented below.

Gauche 3 HOMO
Orbital

Optimisation of Anti 2 Conformer Using a Higher Basis Set

The Anti 2 conformer was optimised using the Hatree-Fock calculation method as before, though this time with the higher basis set 6-31G(d). The details of this calculation are given in the following table.

Gaussian Calculation Information
File Type	.log
Calculation type	FOPT
Calculation Method	RHF
Basis Set	6-31G(d)
Final Energy	-234.611702
Gradient	0.00004313 au
Dipole Moment	0.00D
Point Group	Ci
Calculation Running Time	2 mins 10.4 secs
D-space	Anti 2 Higher

Comparison of Anti 2 Geometry
Basis Set	Geometry
HF/321-G
HF/631-G(d)

It is seen that the bond distances and angles do not vary very much between the two basis sets. Yet looking at the energies there is a difference of 2.91916 Hartree units. This energy change is equivalent to 1831.8 kcal/mol, which shows how changing the accuracy of the basis set greatly affects the energy outcome with little visible change in the molecules structure.

Frequency Analysis of Anti 2

Frequency analysis was conducted on the optimised anti 2 conformer (HF/631-G(d)) Anti 2 Freq. The resulting vibrational modes were all positive, this confirms that the conformer is a local minimum along the potential energy surface. In total 42 vibrational modes were observed yet only 21 are IR active. This comes from the point that there must be a change in dipole moment for a mode to be IR active.

Predicted IR Spectrum of Anti 2 Conformer

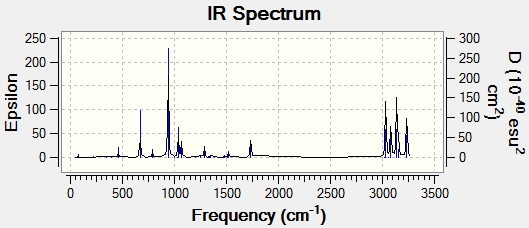
In studying the predicted IR spectrum the peaks that would be of interest are at 1730.95 and 1734.25 wavenumbers. these relate to the symmetric and asymmetric stretches of the two carbon double bonds. The two nodes are visualised below.

Frequency (cm-1)	Vibrational Mode
1730.95 (symmetric)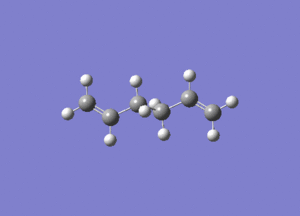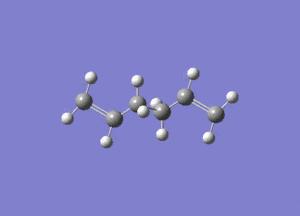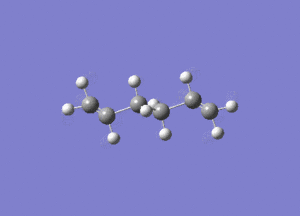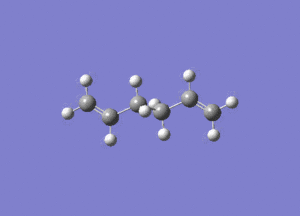
1734.25 (asymmetric)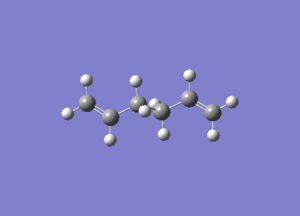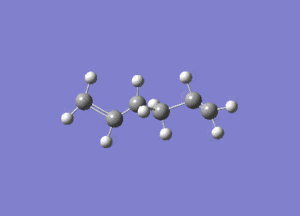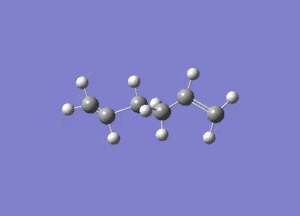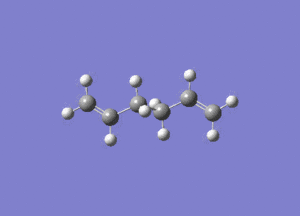

The following thermochemistry data was also obtained from the frequency analysis.

	Energy (au)
Sum of electronic and zero-point Energies	-234.46921
Sum of electronic and thermal energies	-234.46186
Sum of electronic and thermal free energies	-234.50082

Locating the Chair and Boat transition States

Firstly an aryl fragment was optimised (HF/631-G(d))

Calculation Information
J-mol
File Type	.log
Calculation type	FOPT
Calculation Method	UHF
Basis Set	3-21G
Final Energy	-115.82304 au
Gradient	0.00000161 au
Dipole Moment	0.0292D
Point Group	C2v
Calculation Running Time	35.1 sec
D-space	aryl fragment

Optimisation of the Chair Transition State

The optimised aryl fragment was duplicated and the two fragments were arranged in to a chair conformation, with the terminal bond distances set to 0.22 nm. The structure was then optimised with the TS Berny setting using the Hartree-Fock method with a 3-21G basis set. The keyword "opt=noeigen" was added, this stops the calculation from termination if more than one imaginary frequency is detected through the calculation Details of the calculation are given below.

Calculation Information
J-Mol
File Type	.log
Calculation type	FREQ
Calculation Method	RHF
Basis Set	3-21G
Final Energy	-231.61932
Gradient	0.00007526 au
Dipole Moment	0.0292D
Point Group	C2v
Calculation Running Time	29.6 sec
D-space	Chair opt

Frequency analysis of the structure showed an imaginary frequency at -817.8636 cm^-1 which confirms that a transition state has been formed.

Optimisation using Frozen Coordinate Method

The chair transition state was once again located, this time using a frozen coordinated method. Two aryl fragments were arranged into a chair like structure and the terminal bond distances were frozen at 0.22 nm. An optimisation using the TS Berny setting using the Hartree-Fock method with a 3-21G basis set was performed. as before the key words "opt=noeigen" were specified (Chair frozen D-space). the checkpoint file of this calculation was opened and the terminal bonds were unfrozen and set to derivative. The optimisation was performed again as previous, this time however the second derivative of the terminal bond lengths is calculated to determine the terminal bond lengths at which the transition state lies. Details of the final calculation are given below:

Calculation information
J-Mol
File Type	.log
Calculation type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Final Energy	-231.61932
Gradient	0.00005629
Dipole Moment	0D
Point Group	C2h
Calculation Running Time	1 mins, 6.1 secs
D-space	Chair Frozen Method

Frequency analysis showed an imaginary frequency at 818.02 cm^-1, confirming that a transition state has been isolated.

Optimisation of the Boat Transition State

QST2 Method

The QST2 method was used to locate the boat transition state. In this procedure the reactant and product are input and the transition state that is located between these two structures is isolated. Below the anti-2 conformer is seen both as the reactant and the product. It should be noted that care had to be taken when assigning numerical labels to both the carbons and the hydrogens.

An optimisation with the TS QST2 setting was performed using Hatree-Fock method with a 3-21G basis set. Details of this calculation are given below.

Calculation Information
J-Mol
File Type	.log
Calculation type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Energy (RAM1)	-231.61932
Gradient	0.0000391
Dipole Moment	0.0D
Point Group	C2h
Calculation Running Time	15.6 secs
D-space	QST2 method

Frequency analysis shows that an imaginary frequency is present yet looking at the J-mol for this transition state it is clear that the boat conformer had not be located. This can be accounted for by the Gaussian programme's inability to rotate bonds throughout the calculation.

With this failing the reactant and products dihedral angles were set to 0 degrees to resemble the boat transition state. The optimisation to locate the transition state was conducted using the same methods as previous.

Calculation Information'
J-Mol
File Type	.log
Calculation type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Energy (RAM1)	-231.60280
Gradient	0.00003238
Dipole Moment	0.00003238D
Point Group	C2v
Calculation Running Time	13.5 secs
D-space	QST2 Boat

Frequency analysis of the structure showed an imaginary frequency at -839.39 cm^-1, confirming a transition structure being formed. Looking at the J-mol for this structure it can be seen it is the desired boat transition state.

IRC

Intrinsic reaction coordinate analysis was used to find which conformer the chair transition state had emerged from. The calculation takes the structure to a minimum by making small changes to the atomic coordinates as to follow the potential energy surface downwards. The analysis was performed on the chair transition state generated from the frozen coordinate method and was only performed in one direction due to the reactant and product being the same. This was done in 50 steps and the force constants were always calculated for each step. A Hartree-Fock method was used with 3-21G basis set.

Calculation Information
J-Mol
File Type	.log
Calculation type	IRC
Energy (RHF)	-231.68864
Gradient	0.00071154
Dipole Moment	0.0D
Point Group	C2
Calculation Running Time	13 mins 47.8 secs
D-space	Chair IRC

IRC Visualisation	Reaction Coordinate

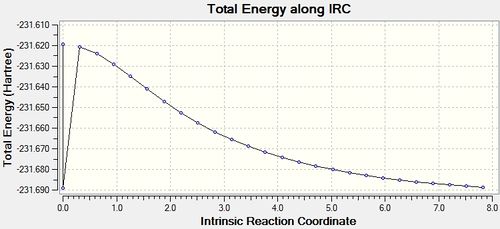
As can be seen from the gradient the calculation was not successful in reaction a minimum. There are different methods of combating this problem. One of which is to further optimise the structure generated from the IRC. This is shown below with the IRC structure being optimised with the TS Berny setting, Hartree-Fock method and with a 3-21G basis set.

Calculation Information
J-Mol
File Type	.log
Calculation type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Energy (RHF)	-231.69199702
Gradient	0.00000286
Dipole Moment	0.680D
Point Group	C2
Calculation Running Time	1 min 1.5 secs
D-space	Chair IRC further OPT

It can be seen from the gradient value of 0.00000286 that the calculation has been successful in isolating the reacting conformer. Another method of successfully isolating the reactant is to perform another IRC analysis as before, though instead of calculating the force constants just at the start of the calculation calculate them throughout the calculation. This was undertaken and the details are shown below.

Calculation Information
J-Mol
File Type	.log
Calculation type	IRC
Energy (RHF)	-231.61932
Gradient	0.0000563
Dipole Moment	0.0D
Point Group	C2
8mins 52.2 secs
D-space	Chair IRC

IRC Visualisation	Reaction Coordinate

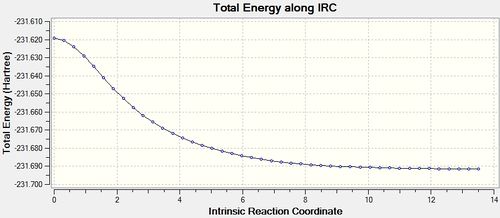
This IRC appears to have been successful with regards to the gradient being 0.0000563.

The outcome of the IRC anaylsis has shown that the transition state leads to the gauche 2 conformer.

Optimising Transition States With a Higher Basis Set

The previously optimised chair transition state from the frozen coordinate method was optimised further using a higher basis set, DFT/6-31G(d).

Calculation Information
J-Mol
File Type	.log
Calculation type	FTS
Calculation Method	B3LYP
Basis Set	6-31G(d)
Energy (RHF)	-234.5569826 au
Gradient	0.00000503 au
Dipole Moment	0.0001D
Point Group	C22h
Calculation Running Time	8 mins 52.4secs
'D-space	Chair 6-31G9(d)

Frequency analysis of the structure showed one imaginary frequency at -565.69 cm ^-1 confirming the structure is a transition state.

For the further optimisation of the boat transition state it was not possible to just copy the structure from the HF/3-21G optimisation and run a DFT/6-31G(d) as the calculation would fail run. For this reason a frozen coordinate method was used to optimise the transition state further. The terminal bonds were initially frozen at 0.22 nm and optimised before being unfrozen and optimised again.

Calculation Information
J-Mol
File Type	.log
Calculation type	FTS
Calculation Method	B3LYP
Basis Set	6-31G(d)
Energy (RHF)	-234.54309
Gradient	0.00003946
Dipole Moment	0.0617D
Point Group	C2v
Calculation Running Time	7 mins 23.6secs
'D-space	Boat 6-31G9(d)

frequency analysis of the structure showed one imaginary frequency at -530.81 cm^-1, confirming the structure is a transition state.

With the frequency analysis of both the chair and boat transition structures the thermochemistry data was obtained.

DFT/6-31G(d)	'Anti-2 reactant	Chair TS	Boat TS
Sum of electronic and zero-point Energies	-234.46921	-234.41493	-234.40234
Sum of electronic and thermal energies	-234.46186	-234.40910	-234.39601
Sum of electronic and thermal free energies	-234.50082	-234.44382	-234.43175

Using this data it was possible to work out the activation energy of the reaction at 298.15K and at 0K, in respect to the anti 2 conformer. This is simply done by finding the difference in energies between the 1,5-hexadiene and the transition states. The activation energies are summarised in the table below.

Transition State	Chair	Boat
Ea 0K	0.05428	0.06687
Ea 298.15K	0.05276	0.06585
Ea 0K (kcal/mol)	34.061	41.962
Ea 298.15K (kcal/mol)	33.107	41.322

These values calculated are near exact to those that are provided in the "appendix 2" of the module instructions. The activation energy of the formation of the chair transition state is significantly lower than the boat suggesting that the chair is the preferred route of reaction. If it is assumed that the product exists in the same conformation as the reactant then under both thermodynamic and kinetic conditions the reaction will proceed through the chair transition state.

Diels-Alder Reaction

Diels-Alder reaction are [6+2] cycloadditions that occur between a conjugated diene and another pi bond, which is known as the dienophile. The reaction leads to the formation of a new six membered ring. These reactions tend to be enthalpically favoured due to the formation of two sigma bonds by the sacrifice of two pi bonds. Although there is a small decrease in the entropy as these reactions proceed they still tend to remain thermodynamically favoured.

The simplest of this class of reaction is the reaction of cis-butadiene with ethene. As these two molecules approach each other there is a need for maximum overlap of the frontier orbitals to proceed to through a transition state to the product, cyclohexadiene. This maximum overlap occurs when the transition state adopts an "envelope" structure.

Simplest Diels-Alder Reaction

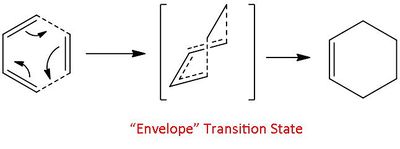
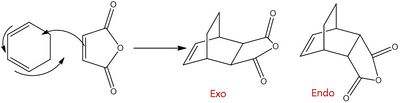
As the reactants become more complicated issues of isomer selectivity arises. This is the case in the reaction of maleic anydride with 1,3-cyclohexadiene. Two products can form, an exo adduct or an endo adduct. Under irreversible kinetic conditions it is known that the endo product is preferred.

Reaction of Maleic Anhydride with 1,3-Cyclohexadiene

cis-Butadiene with Ethene

Optimisation of Cis-butadiene and Ethene

Initially a cis butadiene and ethene molecule where constructed using the fragment tool in Gaussview. Each molecule was indpendantly optimised using an AM1 semi-emperical molecular orbital method. Details of these optimisations are detailed below.

	Ethene	Cis butadiene
J-Mol
File Type	.log	.log
Calculation type	FOPT	FOPT
Calculation Method	RAM	RAM1
Basis Set	ZDO	ZDO
Energy (RHF)	0.02619	0.04879 au
Gradient	0.00000945	0.000089 au
Dipole Moment	0D	0.0414D
Point Group	D2h	C2
Calculation Running Time	7 secs	13.1 secs
D-space		Cis-butadiene

Looking at the HOMO and LUMOs for both cis butadiene and ethene. In the case of cis butadiene the LUMO is symmetrical in terms of the plane of symmetry and the HOMO is anti-symmetrical. For ethene the reverse is true, where the LUMO is anti-symmetrical in terms of the plane of symmetry, while the HOMO is symmetrical. These orbitals mirror well the orbital outcome when using LCAO.

Locating the Transition State using AM1

When modelling the transition state it is beneficial for there to maximum overlap between the the respective HOMO and LUMO of the reactants. This is achieved by the transition state adopted what can be called an "envelope" structure. In Gaussview this envelope structure was constructed using the previosly optimised cis butadiene and ethene. The transition state was optimised using a frozen coordinate method as done in the Claisen rearrangement study, initially freezing the terminal bond distances to 0.22nm. The results of this optimisation are shown below.

Transition State Bond Distances

Calculation Information
J-Mol
File Type	.log
Calculation Type	FREQ
Calculation Method	RAM1
Basis Set	ZDO
Energy (RAM1)	0.11165
RMS Gradient	0.00002495
Dipole Moment	0.5605D
Point Group	C1
Calculation Time	4.7 secs
D-space	Transition State AM1

Frequency Analysis

The frequency analysis of the structure showed an imaginary frequency at -956.00 cm^-1, thus proving that a transition state has been formed. This vibrational mode is visualised below. It can been that the two fragments are approaching each other in a synchronous manner, relating to concerted bond formation. Looking at the lowest real frequency at 147.02 cm^-1 the fragments do not approach each other therefore it is not a bond forming vibrational process.

Imaginary Vibrational Mode-956.00 cm^-1

Lowest Real Vibrational Mode 147.02 cm^-1

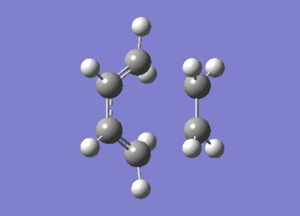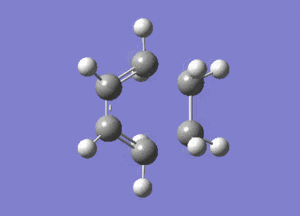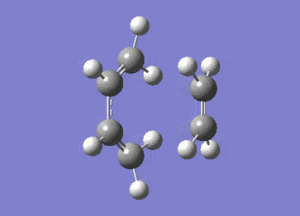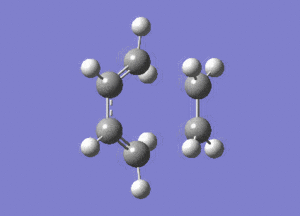
The typical sp³-sp³ bond length is approximately 0.154nm and the typical sp²-sp² carbon bond length is 0.135nm . Looking at the ethene fragment bond length within the transition state its length is 0.138 nm. This is what would be expected of a bond in a transition between a double bond to single bond. The terminal bond distances, 0.212nm are considerable larger than the typical carbon single bond. If it is taken to account that the carbon van der Waals radius is 0.170nm it can be assumed that there is still some degree of bonding interactions between the terminal carbons.

IRC Analysis

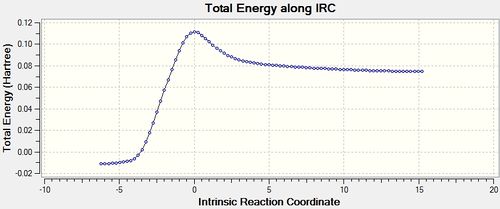
Intrinsic reaction coordinate analysis was performed on the transition state, IRC D-space. This showed that the transition state located was that between the reaction of ethene and cis-butadiene in forming cyclohexene.

IRC Visualisation	Reaction Coordinate

Looking at the reactive coordinate graph there is one transition state. The product, to the left of the graph, is at a lower energy than the reactants, to the right of the graph, indicating that the reaction is thermodynamically favoured.

MO Analysis

Woodman-Hoffman rules can be used to predict whether a pericyclic reaction will occur under thermal or light absorption conditions. For a Diels-Alder reaction under thermal conditions it is necessary that the HOMO of the dienophile and the LUMO of the diene posses the same symmetry as well as the LUMO of the dienophile and the HOMO of the diene.

HOMO-LUMO Interactions of Ethene and Cis-butadiene

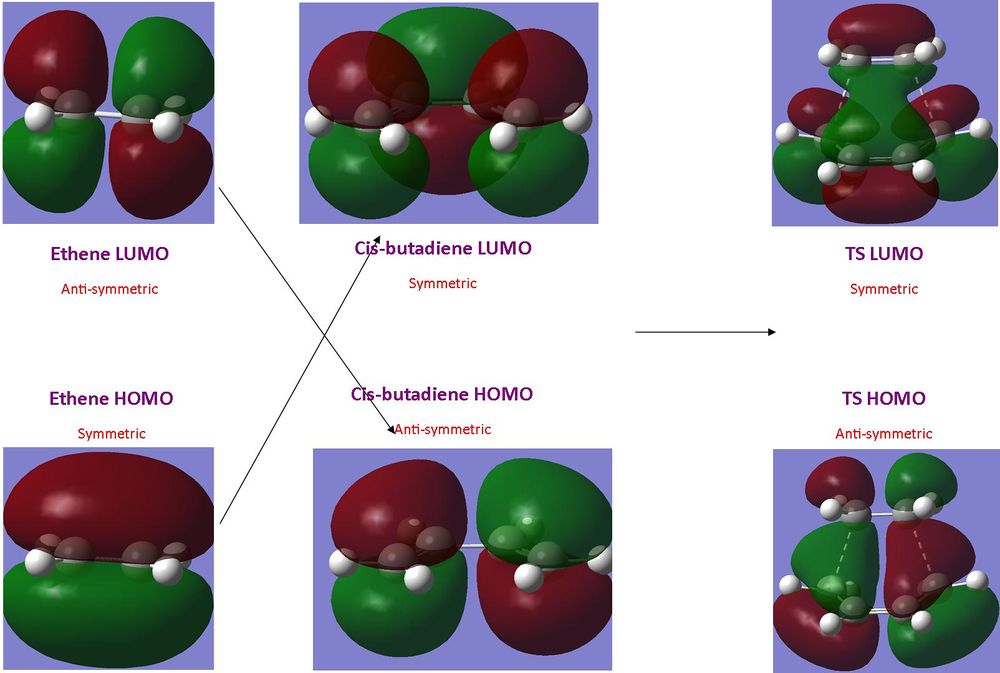
It can be seen in the illustration above that the HOMO of ethene and the LUMO of cis-butadiene are both symmetrical in terms of the plane of symmetry and the LUMO of ethene and HOMO of cis-butadine are anti-symmetrical in terms of the planes of symmetry. This leads to the HOMO in the transition state being formed from the ethene LUMO and the cis-butadiene HOMO, the LUMO of the transition state is formed from the interactions between the ethene HOMO and the cis-butadiene LUMO.

Locating the Transition Stater Between Maleic Anydride and 1,3-cyclohexadiene

Optimisation of Maleic Anhydride and 1,3-cyclohexadiene

As in the previous location of a Diels-Alder transition state both maleic anhydride and 1,3-cyclohexadiene were independently optimised using DFT method and a 6-31G(d) basis set. The details of these optimisations are given below.

	Maleic Anydride	1,3-cyclohexadiene
J-Mol
File Type	.log	.log
Calculation type	FREQ	FREQ
Calculation Method	RB3LYP	RB3LYP
Basis Set	6-31G(d)	6-31G(d)
Energy (RB3LYP)	-379.28954	-233.41891
Gradient	0.00008939	0.0000345au
Dipole Moment	4.0722D	0.378D
Point Group	C2v	C2
Calculation Running Time	3 mins 51.6 secs	2 mins 56.3 secs
D-space	Maleic Anhydride	1,3-cyclohexadiene

Looking at the relative HOMO and LUMOs for the two reactants it can be seen that the LUMO of the maleic anhydride is closer in energy to the HOMO of the 1,3-cyclohexadiene leading to "stronger" interactions between the orbitals. This is due to the electronegativity of the O=C-O-C=O fragment which will lower the energies of the frontier pi orbitals. While these HOMO-LUMO interactions are greater the difference in energy between the HOMO of maleic anhydride and LUMO of 1,3-cyclohexadiene leading to "weaker interactions" between these orbitals. The Klopman-Salem equation dictates that one "strong" interaction and one "weak" interaction is favoured over two "medium" interactions between orbitals.

1,3-cyclohexadiene-Maleic Anhydride HOMO-LUMO Interactions

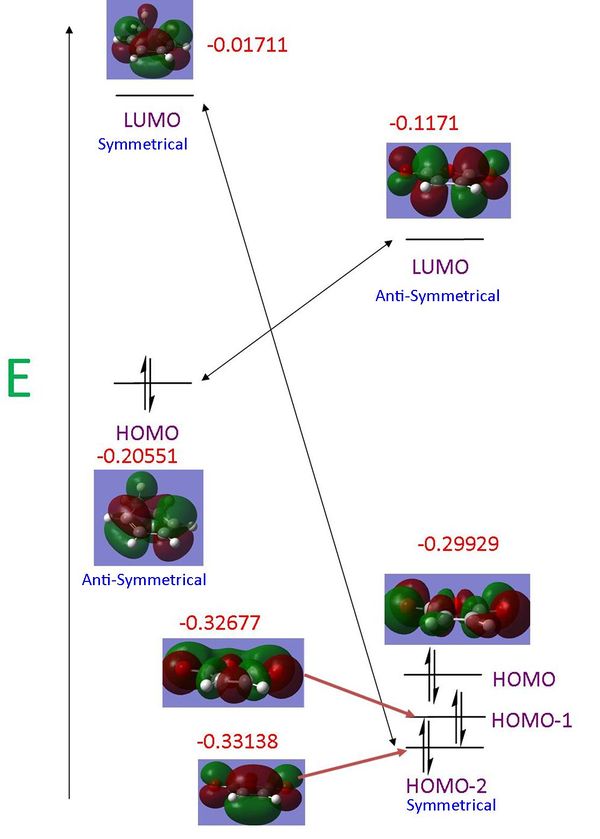
In the case of the maleic anhydride it is not the HOMO involved in the bond formation but the HOMO-2. It should be noted that this is due to the optimisation method used, where the MOs are generated through solving the Schrodinger equation alone. Maleic anhydride was optimised again using a semi-emperical AM-1 method (D-space Maleic Anhydride Semi-emperical). It is seen that in this case the pi orbital involved in the Diels-Alder reaction is in fact the HOMO. The semi-emperical method uses experimentally obtained data and manipulates it when generating the MOs.

Maleic Anydride HOMO Calculated Semi-Empirically

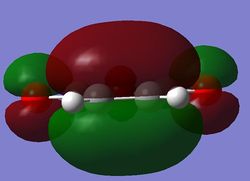
Locating the Exo Transition State

The two transition states were found using the frozen coordinate method conducted previously. Firstly the exo transition state was constructed in gaussview and the terminal bond lengths frozen to a guess length of 0.230 nm. The structure was optimised using the TS Berny optimisation tool with a DFT method and 631-G(d) basis set. The bonds were then unfrozen and then further optimised. Details of this calculation are given below.

Exo Transition State Geometries

Calculation Information
J-Mol
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d)
Energy (RAM1)	-612.67931
RMS Gradient	0.00001514
Dipole Moment	55.071D
Point Group	Cs
Calculation Time	18mins 48.6secs
D-space	Transition State Exo

Frequency analysis of the structure show one imaginary frequency at -448.51 cm^-1, confirming a transition state has been located.

As expected the bond lengths in the newly forming are similar to those in the ethene-cis-butadiene transition state. Though it should be noted that the terminal bond distances are longer in the maleic anhydride transition states. The distance of 0.229 nm is still less than twice the carbon van der Waals radius of 0.340 showing that there is still bonding interactions between the two fragments. Frequency analysis shows that there is an imaginary frequency at -448.51 cm^-1 confirming the calculation has resulted in the transition state.

IRC analysis was conducted on the exo transition state(D-space exo IRC).

IRC Visualisation	Reaction Coordinate

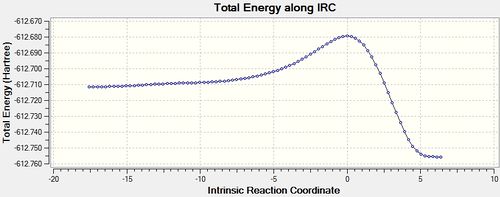
The reaction coordinate profile has the reactants on the left and the products towards the right, this profile indicates that the reaction is thermodynamically favourable.

Locating the Endo Transition state

The endo transition state was locating in the same way as the exo. Firstly the optimised maleic anhydride and the 1,3-cyclohexadiene fragments were positioned together to resemble the endo transition state. The terminal bond distances were set to 0.23 nm, the structure was optimised using the TS Berny optimisation tool with a DFT method and 631-G(d) basis set. the bonds in the resulting structure were unfrozen and a further optimisation was conducted, details of which are given below.

Endo Transition State Geometries

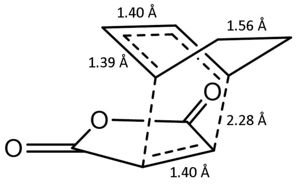
Calculation Information
J-Mol
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d)
Energy (RAM1)	-612.68340
RMS Gradient	0.00001227
Dipole Moment	6.1141D
Point Group	C1
Calculation Time	35 mins 29 secs
D-space	Transition State Endo

Frequency analysis of the structure showed one imaginary frequency at -446.95 cm^-1 confirming a transition state has formed

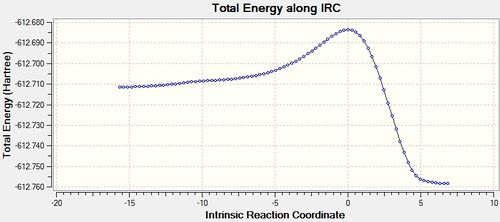
IRC analysis was conducted on the transition state D-space endo IRC

IRC Visualisation	Reaction Coordinate

The IRC shows that the transition state calculated is the one that connects the given reactants and desired products.

DFT/6-31G(d)	'Maleic anhydride+1,3-cyclohexadiene	Endo TS	Exo TS
Sum of electronic and zero-point Energies	-612.52977	-612.50214
Sum of electronic and thermal energies	-612.51940	-612.49179	-612.48766
Sum of electronic and thermal free energies	-612.58644	-612.53833	-612.53427

Product	Endo	Exo
Ea 0K	0.02763	0.03176
Ea 298.15K	0.02761	0.031739
Ea 0K (kcal/mol)	17.336	19.917
Ea 298.15K (kcal/mol)	17.328	19.917

Discussion

When studying the kinetics of a reaction only the energies of the reactants and the transition state need to be considered. From the calculations it has been found that the transition state of the endo lies 2.581 kcal/mol lower in energy that the exo. This stabilisation of the transition state is as a result of secondary orbital overlap occuring in the transition state. In the endo form the formation of the new pi bond lies over the two carbonyl groups of the maleic anydride. A favourable interaction occurs between the lobes of the newly forming pi bond and the lobes of the carbonyl orbitals, overall stabilising the transition state. Looking at the at the terminal bonds the distances between the fragments in the endo transition state are slightly shorter than in the exo. This can be attributed to the secondary orbital overlap drawing the fragments together slightly.

Endo HOMO0-1	Exo HOMO-1
Orbital	Orbital

It is possible to see this secondary orbital overlap in the computed HOMO-1 orbitlal. The pi orbital of the forming pi bond interacts with the in phase pi orbital of the carbonyl, which lies over the oxygen. In the exo HOMO-1 it is clear that this interaction is not present. Both HOMO-1s are symmetric and are therefore formed from interactions between two symmetrical orbitals. These orbitals are HOMO-2 of the maleic anhydride and the LUMO od 1,3-cyclohexadiene.

Conclusion

This project has been successful in introducing basic calculation methods for the study of the transition states in two sets of pericyclic reactions. It has been shown that for the Cope rearrangement the activation energy of going through the chair transition state is 8.225 kcal/mol lower in energy at room temperaure than the boat, implying that this is the favoured reaction route. The second part of the project has looked further into transition states of reactions where there are two possible products. It has been shown that for Diels-Alder reaction between maleic anhydride and 1,3-cyclohexadiene that orbital interactions through the transition state are key in the selectivity of the products.

References

<references>