Rep:Mod:db9127physical

Optimising the Reactants and Products

This project was done to model the Cope rearrangment. In order to do this, we must first model the reactants and products of the reaction. The reaction scheme is shown here:

This reaction can occur via either a boat or a chair transition state. These resemble the conformers of cyclohexane with the same names. The boat transition state is generally accepted to be much higher in energy and therefore less favourable.

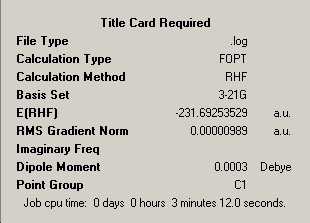
For this reaction the reactant is 1,5-hexadiene. This can occur in many conformers. Firstly, it was optimised for an anti-linkage between the central four carbon atoms. This was done using a HF/3-21G calculation. This created this molecule:

1,5-Hexadiene

The calculation summary is shown here:

The point group of the molecule is actually C_i.

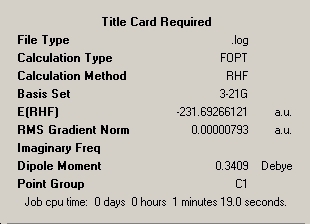
This molecule was then optimised again with a "gauche" linkage in the central four carbon atoms:

1,5-Hexadiene

Here the summary point group is correct. This conformer has a much greater energy than the anti-conformer optimised before. This is due to greater repulsions between non-bonding atoms in the gauche conformer, due to the larger groups being placed closer together. The "anti" conformer already shown should therefore be close to the conformer with the lowest energy, as it has the largest possible dihedral angles between carbon atoms. The alkene group is rotated 60 degrees. This is all anti-1,5-hexadiene, which is the anti2 conformer shown in the appendix of the instructions. This conformer was optimised and found to have an energy of -231.69253529 Hartree. This is the same as the conformer in the appendix.

The anti1 conformer (the first one optimised in this project) was then re-optimised using a higher level of theory, the B3LYP with a 6-31G basis set. This should provide more accurate results. The geometry of the molecule changed very little, implying that for this compound a high level of accuracy is not necessary. The changes that were noted were that the B3LYP model had an energy of -234.55970439 Hartree, ~3 Hartree greater than the HF calculated model. This is a very large difference (~7500kJmol^-1). Also, the HF calculated model had a dipole moment of 0.0003 Debye. This is incorrect, as the molecule should be symmetrical (C_i) and should have no dipole moment. This illustrates well the inaccuracy of the Hartree-Fock level of calculation.

The B3LYP/6-31G level optimised model was then submitted for frequency calculation. This was done using the same level of theory and the same basis set to ensure the correct vibrations were calculated. The calculated IR spectrum for 1,5-hexadiene is shown here:

The peaks at ~3000cm^-1 are all relating to C-H stretches. The large peak at 948cm^-1 is H-C=C bending. The peak at 679cm^-1 is due to C-C=C bending, as are the two peaks at ~1050cm^-1. The peak at 1728cm^-1 is due to C=C stretching.

Thermochemistry The optimised frequency calculation also includes some thermochemical data in the results file. This is recorded here: Sum of electronic and zero-point energies = -234.416245 Hartree Sum of electronic and thermal energies = -234.408955 Hartree Sum of electronic and thermal enthalpies = -234.408010 Hartree Sum of electronic and thermal free energies = -234.447848 Hartree

Optimising the "Chair" and "Boat" transition structures

Firstly, this allyl structure was optimised using HF/3-21G for use as a building block for the transition states:

Allyl

All further optimisations were also done using a HF/3-21G level unless stated otherwise. This optimised allyl was used to create a guess for the "chair" transition state, as shown:

ChairGuess

The distance between the two atoms that were expected to form a bond on the near side was set to 2.2Å. The same was done with the other two atoms expected to form a bond. This structure was then optimised to a transition state. The calculation stopped halfway through so the initial guess transition state was edited slightly to make the calculation easier. This was done by rotating one of the allyl groups to be better aligned with the other. The optimisation process is very sensitive and requires a structure quite close to the final transition state or the calculation will stop. After three changes to the original input, the calculation produced this optimisation of the transition state:

ChairOpt1

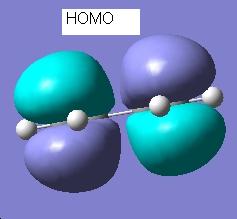
The vibrational frequencies were also calculated as part of the same calculation. An imaginary frequency (one with a negative wavenumber) of magnitude 817.929cm^-1 was found. This corresponds to the formation of the bonds in this reaction, as shown here:

This image clearly shows one bond breaking (the relevant atoms moving apart) as the other bond forms (the atoms moving closer together).

The Chair transition state was then optimised again using a different technique. This technique involves fixing the two bond lengths that are being changed during the reaction, optimising the rest of the molecules, unfixing the bonds and then optimising again. This reduces the amount of computational power required to run the calculations and should also improve the accuracy of the transition state structure. This creates a structure that looks exactly the same as the transitions state first calculated. The reaction bond lengths are the same between the two calculated transition states to 0.0002Å and the dihedral angles across the reaction bonds are the same to within 0.005 degrees. This implies that either method is quite accurate but the second method produced dihedral angles that were 0.009 degrees different from each other, whereas the first method produced dihedral angles that were 0.003 degrees apart. This would imply that the first method was more accurate, as the transition state should be symmetrical and both dihedral angles across the reactive bonds should be the same.

Optimising the "Boat" transition structure

The boat transition structure was optimised using a third method. This involved optimising the reactant and product and using the QST2 method to optimise a transition state from them. The labelling of all atoms has to be the same on the reactant and product for this method to work. The reactant and product used for the calculation are shown here:

This calculation failed. This was due to the limitations of this method, in that it will only work for conformers of the reactant and product that are closer to the reacting conformers. Hence, this reactant and product isomer were submitted to the same technique:

This produced the boat transition state. However, the scan did not complete the frequency calculation due to an error. After this error was fruitlessly searched for, a separate frequency calculation was run on the optimised boat transition state shown:

Boat

This gave an imaginary vibration of magnitude 1016cm^-1, which follows the vectors of the reaction bond formation and breaking in the same way as the chair formation. This greater magnitude implies a greater energy is required for this "vibration" to take place. This is concurrent with the boat transition state being of greater energy.

Optimising the reactant to find the activation energies

The activation energies for the Cope rearrangement via each transition state can be calculated using our transition state models but the reactant is also needed (the activation energy for a reaction is the difference between the transition state and the reactant). However, it is almost impossible to tell which conformation of 1,5-hexadiene is the reactant from the transition states. So a further calculation must be run. This is known as the IRC (Intrinsic Reaction Coordinate) method. The transition state is taken as a starting point and the molecule is changed slightly to a lower energy many times until a minimum energy is reached. This should be the reactant conformer, as energy would be required to change conformation and so, if the calculation stops at the first minimum, it should hit the conformation of the reactant that is closest to the transition states. This was run using the chair transition state calculated with the second method. This produced 50 steps towards the reactant molecule. 50 steps was set as the maximum number of steps so this final step would not have produced the reactant, but it was close enough to optimise the structure from there and avoid using too much computational power and time. This produced this reactant:

Reactant

This is the same as the gauche3 conformer in appendix 1 of the instructions. The reactant energy was -231.69166702 a.u. The chair transition state (as calculated by the first method) energy was -231.61932247 a.u. The chair transition state (as calculated by the second method) energy was -231.61932241 a.u. The boat transition state energy was -230.06026147 a.u. This makes the activation energy for the "chair" mechanism 45.397kcal mol^-1. The activation energy for the "boat" mechanism is 1023kcal mol^-1. This is clearly incorrect, as the experimental value is 44.7kcal mol^-1. Clearly, the gauche3 conformer is not applicable as the reactant for the boat transition state. However, the calculated activation energy for the chair conformation is very close to the value above (46.9kcal mol^-1). This implies that the method has worked correctly and the optimisation of the reactant instead of continuing the IRC method made a minimal difference. Indeed, the energy obtained here is closer to the experimental activation energy of 33.5kcal mol^-1.

Diels-Alder Cycloaddition

cis butadiene was optimised and the HOMO and LUMO were calculated. They are shown here:

The HOMO is clearly antisymmetric to the plane, whereas the LUMO is symmetric to the plane.

The addition of cis butadiene to ethylene was then studied and the transition state optimised using the method that was used to create the "boat" transition state. This was the transition state formed:

Cyclohexene

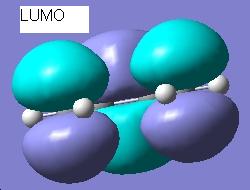
This is formed from the ethylene molecule on the left bonding with the cis butadiene molecule on the right. The two very long single bonds are the bonds being formed. These bonds are longer than the others (2.2095Å compared with 1.370Å) because they were set to be 2.2Å apart when the optimisation was started. However, the bond lengths were not restricted during the calculation. These bonds should be longer than any other bonds in the transition state, as they are single bonds being formed, whereas all the other bonds in the transition state are double bonds being formed or broken. Double bonds are much shorter than single bonds, due to the greater number of electrons present between the two carbon atoms causing an attractive force and screening repulsion. The LUMO of the transition state is shown here:

This clearly shows the HOMO of the ethylene overlapping with the LUMO of the cis butadiene. This is the reaction pathway and it is symmetric. This reaction is allowed because the HOMO of one reactant is overlapping with the LUMO of another. There is significant overlap because the two MOs have the same symmetry. To further illustrate the symmetry of the transition state and the reaction pathway, the imaginary vibration frequency (818cm^-1) is shown here:

It can be seen that the two bonds are formed synchronously. The lowest positive frequency shows the asynchronous movement along these vectors.