Rep:Mod:db9127inorganic
BH3 Introduction Molecule
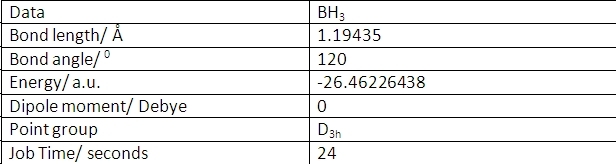
BH3 was optimised using an FOPT calculation type with the RB3LYP method with a basis set of 3-21G. This method means that the molecule is calculated using the Schrődinger equation. This calculates the energy of different geometries and minimises the energy. This geometry with the smallest energy value should be the most stable conformation of the molecule. The basis set 3-21G is a very simple basis set so the calculation will not be extremely accurate but will run quickly. This calculation created a .log file, which gave the optimised geometry and the following information about the optimised molecule:
The molecule is trigonal planar, hence the D3h point group. This gives the bond angle of 120 degrees. BH3 is trigonal planar due to the pz orbital being non-bonding and unoccupied. This is because boron only has 3 electrons and is clearly shown by the molecular orbitals in the later section.
BCl3
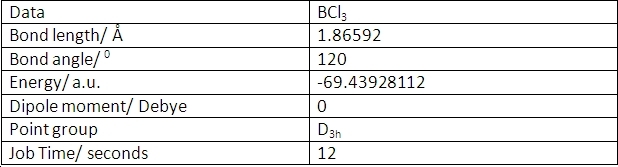
BCl3 was optimised using the same method as BH3. However, the basis set used was LANL2MB. This is a more complex basis set than 3-21G so should give a more accurate optimisation. This gave the following data:
BCl3 has a longer bond length than BH3. This is primarily because chlorine is a larger molecule than hydrogen. It also means that the calculation took less time (12s as opposed to 24s). This is because the optimisation works by moving the atoms from far apart to closer together and the BCl3 took less steps to find the optimised geometry because the final molecule was closer to the starting point of the calculation.
BCl3 also has a much lower energy than BH3. This implies that BCl3 is more stable. This is correct as the energy calculation for a chlorine atom is also far lower than that of a hydrogen atom. This is because chlorine contains more electrons and protons so has greater attractive forces acting on the molecule. The BCl bond is also stronger than the BH bond. This is due to secondary overlap from the lower lying orbitals in the chlorine atoms.
BCl3 has the same geometry as BH3. This is again due to the low number of valence electrons present in a boron atom.
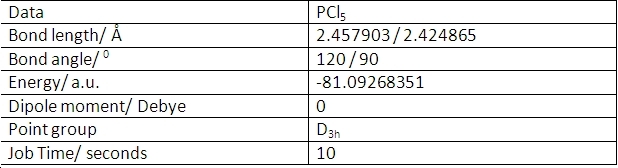
PCl5
PCl5 was optimised using the same method as for BCl3 with the same basis set. The calculation took 34 seconds. This time is because the molecule is more complex than the previous molecules and the Schrõdinger equation takes longer to solve. This gave the following data:
GaussView does not show the P-Cl bonds because the atoms are too far apart. This is merely a graphical issue - the bonds are still there as far as the calculations are concerned. In fact, it is somewhat difficult to define a bond, given that a bond is the overlap of molecular orbitals with the same symmetry to create a lower energy orbital and so-called "non-bonding" orbitals still have some overlap effects with others. Since the gaussian calculation takes into account the molecular orbitals, the definition of a bond does not affect the optimised geometry.
PCl5 is trigonal bipyramidal. The co-ordinates of the atoms are shown here:
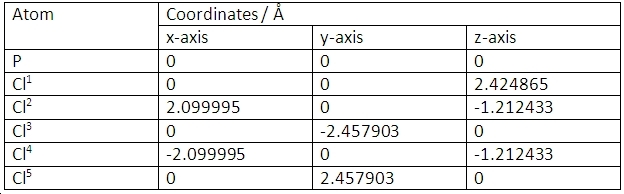
The slightly shorter bond length is for the P-Cl bonds parallel to the y-axis, as denoted by the co-ordinate values. This is because these chlorine atoms are 90 degrees from 3 other chlorine atoms. The equatorial chlorine atoms are 90 degrees from the two axial chlorine atoms and 120 degrees from the other equatorial chlorine atoms so suffer a slightly greater repulsion from them. Hence, they are slightly further from the phosphorus atom and have a slightly weaker bond. This makes the equatorial chlorine atoms more susceptible to substitution reactions.
Vibrational analysis of BH3
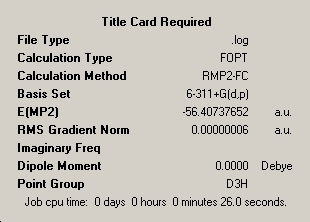
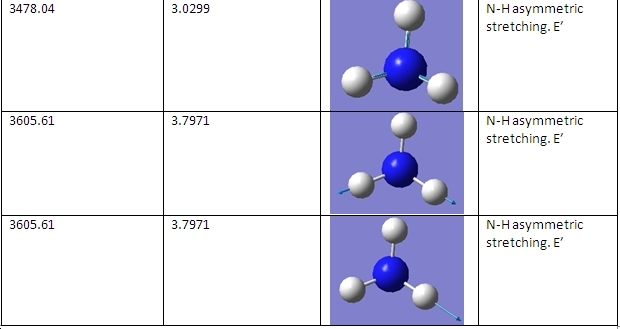
The vibrational frequencies of BH3 were calculated. They are shown here:
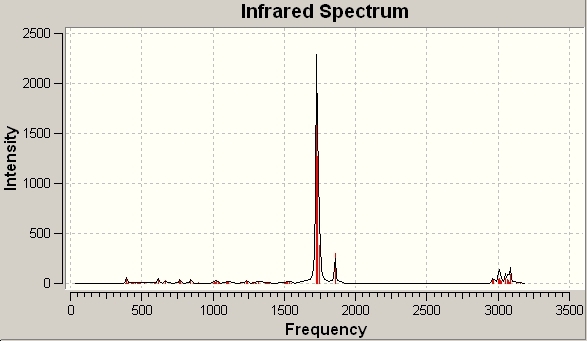
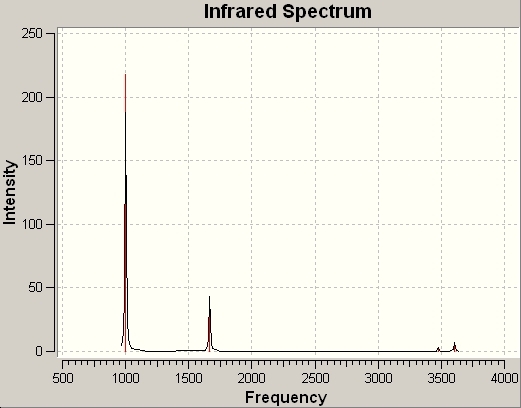
The IR Spectrum for BH3 is shown here:
Only 3 peaks are shown on this spectrum, despite there clearly being 6 vibrations for BH3. This is because the two B-H stretching vibrations occur at the same frequency, as do two of the bending vibrations. The symmetric bending stretch is also not present in the IR spectrum, as it does not change the symmetry of the molecule.
Molecular Orbitals of BH3
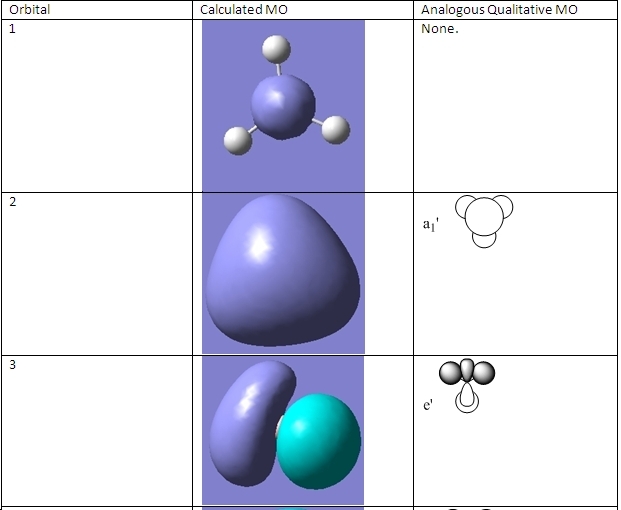
The MOs for BH3 were also calculated using Gaussian and compared to qualitative molecular orbitals. The qualitative MO diagram for BH3 is shown here:
The occupied MOs and LUMO were calculated and are shown here. The other unoccupied orbitals were not calculated as they become more diffuse and therefore have odd forms.
The first calculated MO does not exist. It is there to help the Gaussian calculation by making the molecule BH3-. This is because BH3 has only 6 electrons in the system. The other MOs are analogous with the qualitative MOs shown. These correlate very well, which implies that in the absence of computational software, qualitative MOs are an accurate description of occupied and reactive orbitals. The HOMO orbital can be either orbital 3 or 4 as they both have the same energy (-0.356 a.u.).
All of the occupied MOs are in the same plane as the B-H bonds. This is why BH3 is trigonal planar; the atomic orbitals of boron must have the same symmetry as the atomic orbitals of the hydrogen atoms to form bonds. The first non-planar MO is the LUMO, which is why BH4- is not a planar molecule; the last hydrogen atom bonds with the LUMO which is perpendicular to the plane.
cis- and trans- isomerism of molybdenum complexes
Mo(CO)4L2 complexes were optimised, first loosely using a low level basis set (LANL2MB) and then further using a higher level basis set (LANL2DZ). This was done to make the calculation faster than using a high level basis set immediately. L=piperidine or P(CH3)3. Both the cis and trans isomers were optimised. Unfortunately, the Mo-L bond lengths were too long for GaussView to show them.
The cis-isomers both have slightly increased angles between the L ligands and the CO ligands (91 degrees). This decreases the other inter-ligand angles in the molecule accordingly. The trans-isomers both have all angles at 90 degrees. This difference in angles for the cis-isomers is due to a steric effect from the large CH3 or piperidine groups, repelling the CO ligands.
Literature values for the angles and bond distances in cis-Mo(CO)4(PPh3)2 are shown here compared with the computational values for cis-Mo(CO)4(P(CH3)3)2. The comparison is valid, as we have been using P(CH3)3 as a simplified model for PPh3. This was to lower calculation time and the two ligands should behave similarly.
The literature values were taken from "Steric contributions to the solid-state structures of bis(phosphine) derivatives of molybdenum carbonyl. X-ray structural studies of cis-Mo(CO)4[PPh3-nMen]2 (n = 0, 1, 2)", F. Albert Cotton, Donald J. Darensbourg, Simonetta Klein, and Brian W. S. Kolthammer, Inorg. Chem., 21, (1982), p294-299 DOI:101.1021/ic00131a055
The bond lengths are all very similar. The only major difference is that the PPh3 ligands lie closer to the molybdenum atom. This is because the phenyl rings donate electron density to the phosphorus atom, making it more electron rich and therefore more strongly attracted to the metal centre. The P-Mo-P bond angle for the PPh3 complex is 104.62 degrees. This is far greater than the P-Mo-P bond angle for the P(CH3)3 complex which was 90.93 degrees. The remainder of the bond angles within the computed complex are all ~90 degrees. This shows a large discrepancy from the literature. This is probably due to the simplification of our model, as it removes a large part of the steric effects from the phenyl groups. It may also be because we have not taken into account the presence of d-orbitals in our model. If d-orbitals are taken into account, the calculated P-Mo-P bond angle becomes 92.73 degrees. This is closer to the literature value but implies that the majority of the difference is due to the change in ligand.
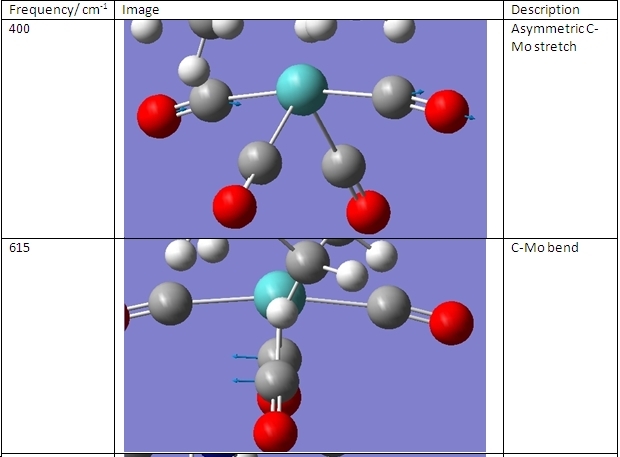
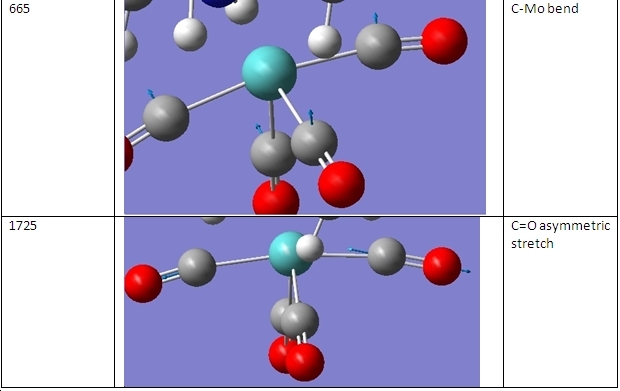
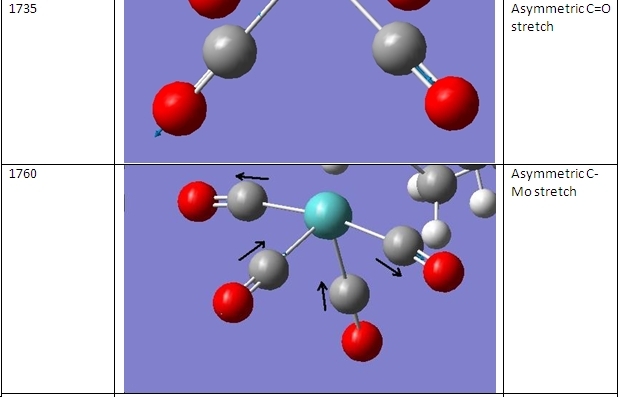
The vibrational frequencies of the cis- and trans- isomers were then calculated. These are shown here:
cis-Mo(CO)4(pip)2
cis-Mo(CO)4(P(CH3)3)2
trans-Mo(CO)4(pip)2
trans-Mo(CO)4(P(CH3)3)2
As can be seen, there are two major comparisons that can be drawn. The first is that the piperidine complexes exhibit four different stretches in the 3000-3300cm-1 region to the two exhibited by the methylphosphine complexes. That is because these vibrations are due to C-H bonds and these are in different environments between these two ligands.
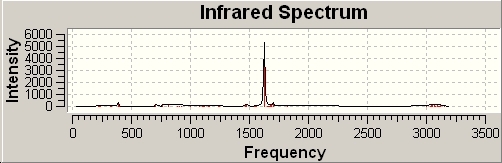
The second comparison to be drawn is that the cis- complexes exhibit a peak at ~1850cm-1 that is not exhibited by the trans- complexes. This stretch is shown below:
In the trans- complexes, this vibration does occur. However, here it is a symmetrical stretch so does not change the dipole moment of the molecule. This means that it is not present on the IR spectrum. The remaining vibrations are assigned in the table below:
Any further peaks were due to various C-H bending vibrations within the ligands.
Following a Reaction Path: The Quantum Nature of Ammonia
Ammonia is an interesting molecule because it readily inverts its structure. This is also true of most trivalent nitrogen atoms but ammonia is easiest to calculate results for and it provides a model for all nitrogen inversion. Ammonia can invert because the activation energy required to reach a trigonal planar transition state is very low. The inversion reaction occurs as shown:
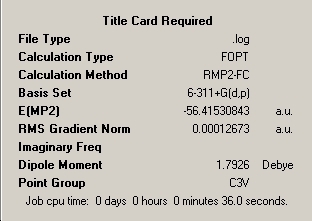
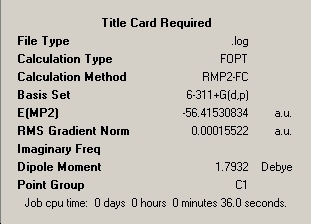
In this section, three isomers of ammonia were optimised and the energies compared. The three isomers were: ammonia in its usually accepted tetrahedral shape; the same shape with one N-H bond length changed to 1.01Å; a trigonal planar ammonia molecule. These isomers will be referred to as 1, 2 and 3 respectively. The summaries of their optimisations are shown here: _____________1____________________________________________2_______________________________________3____________________________
The calculations were then redone using the MP2 method. The same basis set was used to make direct comparison possible. ___________________1____________________________________________2_______________________________________3___________________________
The energy difference between isomers 1 and 2 (the normal geometric state of ammonia and the transition state for inversion) was calculated as ΔE= 16.8595kJmol-1 for the DFT method and ΔE= 20.8252kJmol-1 for the MP2 method of calculation. The literature value for the energy barrier of inversion is 24.3kJmol-1. This implies that the MP2 method is more accurate, as it gives an energy closer to the literature value. However, it should be noted that the basis set chosen makes a very large difference to the energy values (~2000kJmol-1 when changing from 6-31G to 6-311G). The energy also changes slightly each time the optimisation is re-run. Hence, the calculated energy values can never be fully accurate when using either of these methods. A much more complex and time-consuming basis set would be required to achieve a high level of accuracy.
It should be noted also that both of these methods give the energy barrier for inversion as lower than the literature value. This may be due to contributions from neighbouring molecules which the calculations do not take into account.
Vibrational analysis of NH3 isomers
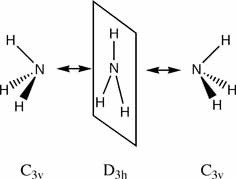
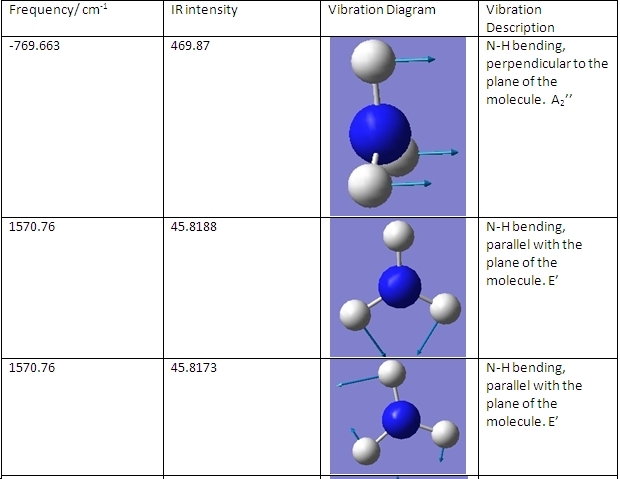
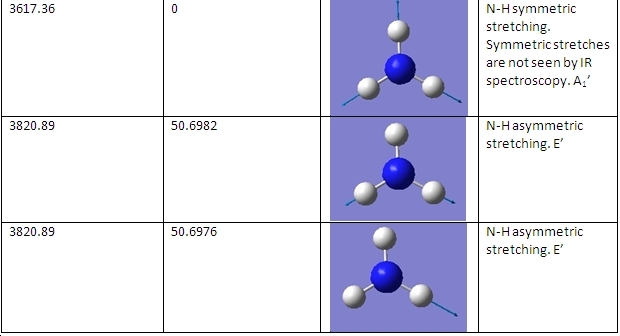
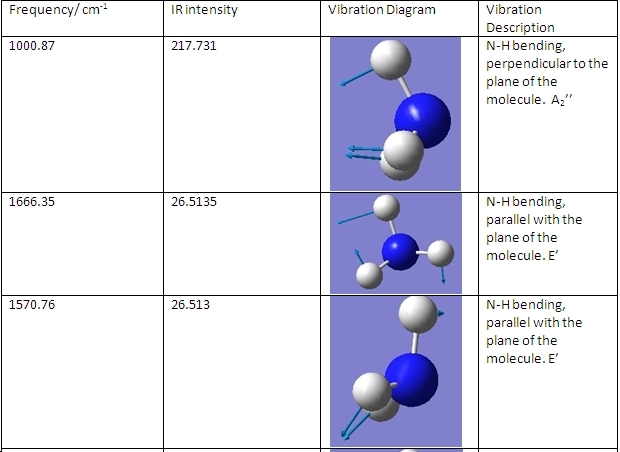
The C3v and D3h models were used to calculate the vibrational frequencies of these conformations for NH3. These vibrations are shown below:
D3h
C3v
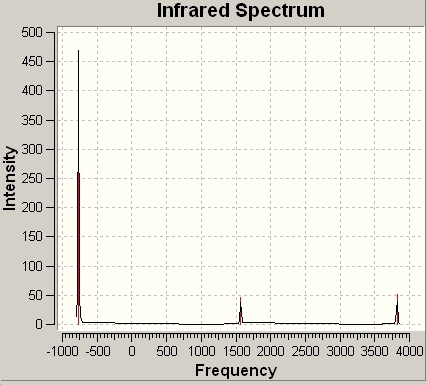
The main differences are the first vibration and the 4th vibration. The first vibration has a greatly different frequency because the D3h isomer vibration changes the dipole moment slightly because the H atoms do not move far from the plane. Because the C3v isomer is already bent, this vibration pushes the H atoms even further from the plane, greatly changing the dipole moment and requiring a greater frequency of vibration. The 4th vibration is different because for the D3h isomer it is a symmetric stretch. This means that it does not show up on IR spectra, as it does not change the dipole moment of the molecule.
The first vibration follows the reaction path (the vectors that the atoms move are the same as those for forming the transition state). This gives it a negative frequency in the transition state, as it requires energy to keep the molecule as it is, rather than to change the molecule.
The IR Spectra of both isomers are shown below: ________________________1_________________________________________________________________2_____________________________________
Mini Project: Fuels of the Future
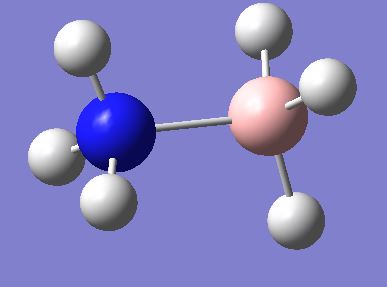
Ammonia borane was optimised in both the eclipsed and staggered conformers. The staggered conformer was found to be more stable by 8.74kJmol-1. This was compared to optimisations of the conformers of ethane, which is-1 isoelectric with ammonia borane. Ethane was found to have a staggered conformer that was more stable by 11.83kJmol-1. This difference is probably due to the increased bond length in ammonia borane. The N-B bond was found to be 1.685Å, while the C-C bond in ethane is 1.544Å. This means that the hydrogen atoms are further apart in ammonia borane than in ethane. Hence, they repel each other less and affect the conformation of the molecule less. Since the orbitals of the hydrogen atoms are the only restraint on the conformation (through repulsion with each other and gauche effects), this makes it easier for ammonia borane to adopt the eclipsed conformation than ethane. The staggered structure of ammonia borane is shown here:
Borane has similar bonding to its isoelectric analog, as the atoms are all bonded via the same number of electrons. They should not have any difference to other molecular orbitals either as the electrons are all the same. However, ammonia borane has a dipole moment of 1.844 Debye, due to the greater electronegativity of nitrogen and the lower electronegativity of boron. This distorts the MOs of ammonia borane, creating greater electron density over the nitrogen atom.