Rep:Mod:db810physical

Transition Structure of the Cope Rearrangement and Diels-Alder [4+2] Cycloadditions

Physical Module 3

Author: Daniel Bisley

Abstract

Introduction to Computational Chemistry

Computational chemistry is the branch of chemistry that applies mathematical, chemical and computing techniques to solve chemical problems. It is a powerful technique that can be used to great effect when certain properties of molecules are required, ranging from electronic structure determinations to potential energy surface calculations. Acquiring such data enables the chemist to form predictions in relation to their reactions before experiments are run, making them better prepared for making observations.

The underlying foundation to all computational chemistry is the Schrödinger equation which can be greatly simplified by applying the Born-Oppenheimer approximation, allowing a wavefunction to be broken down into both electronic and nuclear vibrational and rotational parts. The electronic part of this equation is then solved for electrons only, assuming nuclei are fixed. This greatly reduces the complexity of the algorithms involved in the computational analysis and hence leads to shorter times for a simulated calculation to be made.

Having a large database of chemical compounds at your fingertips is incredible advantageous, especially when the materials under consideration:

• Are too expensive to purchase
• Impose serious health risks (e.g. toxicity, radioactivity)
• Are difficult to synthesise
• Aren't readily available

Optimising Molecules

Figure 1: Potential energy / distance graph for a diatomic molecule.

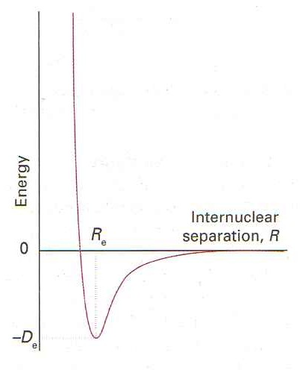
When the Born-Oppenheimer approximation is used on the Schrödinger equation, energy can be obtained as a function of the distance between the fixed nuclei. As the nuclei move closer together, favourable coulombic nuclear-electron interactions result in a decrease in the total energy until a point is reached where the nuclei begin to repel one another, resulting in a rapid increase in energy. This point is known as the equilibrium distance between nuclei and corresponds to a state where there is no force governing which way the nuclei will move relative to each other. For a diatomic, this is summarised in figure 1. This is the potential energy surface (PES) of the molecule and is what is used when carrying out an optimisation in a computational program such as Gaussian™.

From an initial predetermined internuclear distance, Gaussian™ changes this distance and calculates the difference in energy brought about by the change. The gradient at the point is also calculated to determine the force, where the force vector is the negative derivative of potential energy with respect to distance:

$\overrightarrow{F}=-\overrightarrow{\mathrm{\nabla }}U$

When a minimum in energy difference has been determined by sweeping through internuclear distances the gradient will equal zero; indicative of a stationary point and hence equilibrium distance. The length between nuclei in this stable equilibrium state is called the optimised bond distance.

Pseudo-Potentials

For lighter elements, the Schrödinger equation is sufficient to provide reliable results computationally. As the atoms increase in size and mass, relativity starts to affect the calculations which can provide results deviating from expectations.

A way around these relativistic effects is to use a "pseudo-potential" that represents the core electrons in a heavy atom as a function. Although there is an assumption made here that it is the valence electrons alone that determine bonding character, pseudo-potentials are surprisingly accurate.

Basis Sets

A basis set is the linear combination of atomic orbitals needed to define a group of functions to represent molecular orbitals.

When analysing post-second row atoms, where the atomic structure gets more complex, the basis set needs to be improved to describe the electronic structure more accurately. By improving the basis set, the time taken to optimise the molecule increases so there is discrepancy between high accuracy attained and a low CPU times.

The Cope Rearrangement

Figure 2: Overview of the Cope rearrangement mechanism.

The Cope rearrangement is considered a [3,3] sigmatropic rearrangement of 1,5 dienes favoured by the supply of thermal energy, summarised in figure 2 with 1,5-hexadiene, the simplest 1,5-diene.

Mechanistic Controversy

The mechanism governing the Cope rearrangement has been subject to much speculation over the past couple of decades. Scheme 1 represents the the three models that have been the historic focus of mechanistic attention which are also outlined below. These mechanisms involve dissociation to a bis-allyl intermediate, stepwise formation of a diradical tight chair 1,4-diyl intermediate or an aromatic transition state from concerted bond breaking and formation.

Scheme 1: Three proposed mechanism pathways for the Cope rearrangement.

Dissociative Mechanism

The dissociation of 1,5-hexadiene is a radical-based mechanism in which the electron density in the C-3 - C-4 bond is broken evenly to produce a pair of non-interacting allyl radicals. This is followed by their random recombination.

Of the three mechanisms, dissociation is the least credible on thermodynamic grounds. The enthalpy involved in forming an allyl radical is +39.9 ±0.7 kcal mol^-1, meaning two allyl radicals require around +79.7 kcal mol^-1 of energy to form. ΔH_f[1,5-hexadiene] is calculated to be +20.1 kcal mol ^-1, meaning an enthalpy change of +59.6 kcal mol^-1 is required to form the two allyl radicals per mole of 1,5-hexadiene. This is 26.1 kcal mol-1 above the experimental enthalpy of activation of 1,5-hexadiene and so other mechanisms need to be explored to find a better fit to the +33.5 kcal mol^-1 involved in the transition state formation for the Cope rearrangement.

Stepwise Diradical Intermediate Mechanism

An alternative mechanism that was widely championed to be the true pathway for the Cope rearrangement proceeded via a "cyclohexa-1,4-diyl" diradical of C_2h symmetry, where a covalent bond is formed between C-1 and C-6 through radical bond breaking of C-1 - C-2 and C-5 - C-6 alkene bonds. This intermediate then undergoes bond cleavage to either revert to the original 1,5-hexadiene or proceed to the product of rearrangement.

Theoretical calculations put the enthalpy of formation of such a radical at +54.0 kcal mol^-1 , in very close agreement with the experimental +53.6 kcal mol^-1 transition energy value in the Cope rearrangement.

Concerted Aromatic Transition State Mechanism

The final mechanisic proposal is now the most widely accepted through computational calculations; a 6-membered carbon aromatic transition state. Using the B3LYP method with 6-31G* and 6-311+G** basis sets, the energy of the aromatic transition state has been found to be within 1 kcal mol^-1 of the experimental Cope rearrangement enthalpy. Despite this excellent agreement, it is hard (but possible) to determine between the aromatic transition state and the 1,4-diyl intermediate energeticaly using perturbation theory due to the relative flatness of the potential energy surface between 1.64Å and 2.19Å (minimum: 1.85Å)

Both chair and boat transition structures exist for the aromatic transition state:

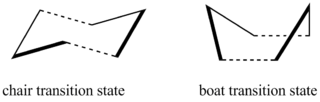
The chair form of the transition state has C_2h symmetry whilst the boat employs C_2v symmetry. Like cyclohexane, the chair structure is expected to be slightly lower in energy than the boat structure due to the minimisation of ring strain and steric effects.

Experimental Aim

The aim of this computational analysis is to calculate the low-energy minima and transition structures on the 1,5-hexadiene potential energy surface to determine a mechanism for the Cope rearrangement. This will be done by optimising the reactant and product 1,5-hexadiene along with both aromatic chair and boat transition states.

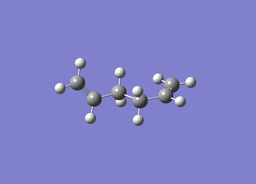
Optimising a Molecule of 1,5-hexadiene

1,5-hexadiene has twelve theoretical conformers, four of which comprise two sets of enantiomeric pairs. Figure X represents these conformations.

Table 1

1,5-Hexadiene Optimisation: 3-21G
Optimised C-C bond length: 1.54371Å Optimised C=C bond lengths: 1.31644Å
File Type	.fch
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Total Energy	-231.69097057 a.u.
RMS Gradient Norm	0.00000304 a.u.
Dipole Moment	0.2955 Debye
Point Group	C1
Job CPU Time	4 minutes 2.2 seconds
DOI:10042/23028

Antiperiplanar Conformation

To begin the analysis, an antiperiplanar arrangement of the two C=C groups for 1,5-hexadiene relative to the central four carbon atoms was drawn in Gaussview™, an interface of the program Gaussian™. This molecule was then optimised at the HF/3-21G level of theory and published to D-space. Table 1 summarises the optimisation procedure.

Table 2

Item Table for 1,5-Hexadiene Optimisation Using a 3-21 Basis Set
Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000002 0.000300 YES Maximum Displacement 0.000674 0.001800 YES RMS Displacement 0.000227 0.001200 YES Predicted change in Energy=-1.733515D-09 Optimization completed. -- Stationary point found.

The above Item table shows that the calculation converged and that a stationary point was found on the potential energy surface. The total energy of the optimised molecule is calculated as -231.69097057 hartrees, corresponding to the anti4 conformer in appendix 1 on the instructions page.

To ensure this stationary point is a minimum, frequency analysis was run on this optimised conformation of 1,5-hexadiene. Table 4 shows that all frequencies are low (within ±15cm^-1) and that none of the larger frequencies are negative; confirmation that a minimum in energy has been achieved.

Table 4

Item Table for 1,5-Hexadiene Frequency Analysis Using a 3-21G Basis Set
Low frequencies --- -2.1226 -0.7752 -0.5520 -0.0007 -0.0006 -0.0005 Low frequencies --- 86.1506 98.5683 153.8017

Table 3: 1,5-Hexadiene Frequency Summary (3-21G)

File Type	.log
Calculation Type	FREQ
Calculation Method	RHF
Basis Set	3-21G
Charge	0
E(RHF)	-231.69097057 a.u.
RMS Gradient Norm	0.00000309 a.u.
Dipole Moment	0.2955 Debye
Point Group	C1
Job CPU Time	32.8 Seconds
DOI:10042/23031

The energy of the molecule after the frequency analysis is similar to that of the optimised 1,5-hexadiene using the 3-21G basis set. This indicates that the frequency analysis was a success and that the molecule was minimised. The "low frequencies" quoted in table 11 are low, which indicates that the motions of the molecule's centre of mass do not significantly interfere with the frequencies we wish to analyse; the first vibration has A symmetry and a frequency of 86.2 cm^-1 which is just over 170,000 times the value of the highest low frequency. These low vibrational frequencies should be as close to zero as possible for the best frequency analysis.

The point group of the molecule was found to be C₁, also in agreement with appendix 1. The Newman projection for this optimised molecule can finally be drawn:

Figure 3: Newman projection for optimised anti4 1,5-hexadiene

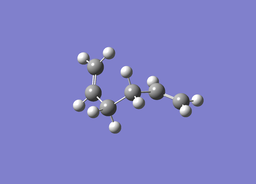
Gauche Conformation

Table 5

1,5-Hexadiene Optimisation: 3-21G
Optimised C-C bond length: 1.54577Å Optimised C=C bond lengths: 1.31666Å
File Type	.fch
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Total Energy	-231.68961574 a.u.
RMS Gradient Norm	0.00001401 a.u.
Dipole Moment	0.4439 Debye
Point Group	C1
Job CPU Time	1 minute 57.6 seconds
DOI:10042/23055

A gauche arrangement of the two C=C groups for 1,5-hexadiene relative to the central four carbon atoms was then drawn in Gaussview™. This molecule was then optimised at the HF/3-21G level of theory and published to D-space. Table 5 summarises the optimisation procedure.

Table 6

Item Table for 1,5-Hexadiene Optimisation Using a 3-21 Basis Set
Item Value Threshold Converged? Maximum Force 0.000027 0.000450 YES RMS Force 0.000008 0.000300 YES Maximum Displacement 0.000991 0.001800 YES RMS Displacement 0.000288 0.001200 YES Predicted change in Energy=-2.507486D-08 Optimization completed. -- Stationary point found.

The above Item table shows that the calculation converged and that a stationary point was found on the potential energy surface. The total energy of the optimised molecule is calculated as -231.68961574 hartrees, corresponding to the gauche5 conformer in appendix 1 on the instructions page.

To ensure this stationary point is a minimum, frequency analysis was run on this optimised conformation of 1,5-hexadiene. Table 8 shows that all frequencies are low (within ±15cm-1) and that none of the larger frequencies are negative; confirmation that a minimum in energy has been achieved.

Table 8

Item Table for 1,5-Hexadiene Frequency Analysis Using a 3-21G Basis Set
Low frequencies --- -0.1894 -0.0005 -0.0003 0.0003 0.1481 0.3476 Low frequencies --- 80.3600 120.0310 136.0630

Table 7: 1,5-Hexadiene Frequency Summary (3-21G)

File Type	.log
Calculation Type	FREQ
Calculation Method	RHF
Basis Set	3-21G
Charge	0
E(RHF)	-231.68961576 a.u.
RMS Gradient Norm	0.00000038 a.u.
Dipole Moment	0.4438 Debye
Point Group	C1
Job CPU Time	33.2 Seconds
DOI:10042/23069

The energy of the molecule after the frequency analysis is very similar to that of the optimised 1,5-hexadiene using the 3-21G basis set. This indicates that the frequency analysis was a success and that the molecule was minimised. The "low frequencies" quoted in table 11 are low, which indicates that the motions of the molecule's centre of mass do not significantly interfere with the frequencies we wish to analyse; the first vibration has A symmetry and a frequency of 80.4 cm-1 which is just over 230 times the value of the highest low frequency. These low vibrational frequencies should be as close to zero as possible for the best frequency analysis.

The point group of the molecule was found to be C₁, also in agreement with appendix 1. The Newman projection for this optimised molecule can finally be drawn:

Figure 4: Newman projection for optimised gauche5 1,5-hexadiene

Identifying Lower Energy Conformers

It is not surprising that the antiperiplanar conformer previously investigated is lower in energy than a corresponding gauche conformation. Both conformers are free from torsional strain, which means the distance between corresponding functional groups in the gauche conformation is smaller than their Van der Waals radii, resulting in unfavourable steric effects that increase the total gauche conformation energy.

Are the calculated anti4 and gauche5 conformations the lowest energy anti and gauche conformers? There are twenty seven theoretical conformations of a six carbon system such as 1,5-hexadiene with equal 60° torsional angles, but only ten of these are unique in this case. All ten of these conformers will have to be optimised at the HF/3-21G level of theory to give a definitive answer as to which conformer can be classed the true minimum (at this level of theory). Table 9 shows the results of these optimisations along with links to the corresponding files. The same methods were used as before to check that the force along the potential energy surface converged at zero.

Table 9: Optimisation Summary Table of 1,5-Hexadiene Conformers at the HF/3-21G Level of Theory

Conformer	Structure	Newman Projection	Point Group	Total Energy/Hartrees HF/3-21G	Relative Energy kcal mol-1	Optimisation Files
gauche1			C2	-231.68771617	3.10	DOI:10042/23077
gauche2			C2	-231.69166701	0.62	DOI:10042/23082
gauche3			C1	-231.69266121	0.00	DOI:10042/23078
gauche4			C2	-231.69153035	0.71	DOI:10042/23084
gauche5			C1	-231.68961574	1.91	DOI:10042/23055
gauche6			C1	-231.68916020	2.20	DOI:10042/23102
anti1			C2	-231.69260220	0.04	DOI:10042/23083
anti2			Ci	-231.69253516	0.08	DOI:10042/23085
anti3			C2h	-231.68907062	2.25	DOI:10042/23086
anti4			C1	-231.69097057	1.06	DOI:10042/23028

It can be seen from table 9 that the gauche3 conformer is in fact lower in energy than all of the antiperiplanar conformers. The energy of this minimum structure has therefore been assigned a relative energy of 0.00 kcal mol^-1 so that the other total energies can be presented with respect to this reference (1 hartree = 627.509 kcal mol^-1).

To account for this surprising preference towards the gauche3 conformation, the three effects that govern confirmation need to be considered.

1) Orbital Overlap / Bond Orientation

Favourable orbital interactions can lower the energy of a particular conformation, especially when considering C-H bonds on neighbouring carbon atoms. Favourable alignment of the σ_C-H and σ*_C-H orbitals in antiperiplanar conformations results in overall stabilisation if the σ-σ* energy gap is sufficiently small. For example, in staggered ethane there are six equivalent anti-periplanar interactions between pairs of a σ_C-H orbital and a σ*_C-H orbital, each of which has a stabilisation energy of around 3.3 kcal mol^-1. As only two electrons are involved in such interactions, the resulting antibonding orbital (which is more destabilising than the bonding orbital is stabilising) is not filled, resulting in overall stabilisation. Gauche interactions are also stabilised by this effect, but it is maximised with antiperiplanar conformations.

2) Pauli Repulsions

The interaction between two occupied σ_C-H orbitals results in overall destabilisation, due to the filled antibonding molecular orbital being more destabilising than the bonding orbital is stabilising. Therefore the pairwise (steric) repulsions can be minimised by adopting an antiperiplanar conformation.

3) Dispertion Forces

Effects 1 and 2 operate at relatively short internuclear distances. At longer non-bonded interatomic distance, dispertion forces take effect as illustrated in figure 1. As the internuclear distance decreases, favourable electron-nuclei interactions lower the interaction energy until a point is reached when the nuclei start to repel one another, increasing the interaction energy at a rapid rate. Therefore the maximum attraction between atoms is equal to the sum of their Van der Waals radii.

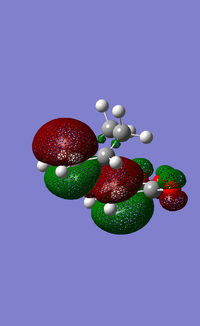
Effects 1 and 2 both favour the antiperiplanar conformation of 1,5-hexadiene, meaning a favourable Van der Waals interaction must result in a decrease in energy for the gauche3 conformation. By inspecting the molecule, it is clear that a vinyl hydrogen atom is in the vicinity of a C=C π orbital, possibly leading to isotropic stabilisation. A molecular orbital analysis was carried out to see if this interaction could be visualised.

Table 10: Comparison of HOMOs for anti2 and gauche3 Conformations

anti2 HOMO (HF/3-21G)	gauche3 HOMO (HF/3-21G)
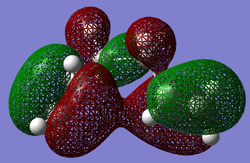
DOI:10042/23100	DOI:10042/23101

The orbitals that are generated are called natural bond orbitals, or NBOs. In 1979, Brunck and Weinhold derived equations to obtain these orbitals, which is the basis of the molecular orbital analysis resulting in the HOMOs we can see in table 10.

It is in fact the interaction between the two terminal C=C π orbitals that results in the strong interaction (lower red lobes) for the gauche3 conformation. The vinyl H-π interactions are present in both conformations. At this level of theory, this is clearly the cause for the lower energy of the gauche3 relative to anti1 and anti2 conformations. However, the conformational theory discussed above still points towards an antiperiplanar minimum in energy. Effect 1 stabilisation in particular, along with that of effect 2 should outweigh this favourable electronic interaction (effect 3). This could suggest that the level of theory is unsuitable for reliable conformational energy analysis. The relative total energy difference between gauche3 and anti1/anti2 conformations is 0.04 and 0.08 kcal mol^-1 respectively at this level of theory, a very small amount of energy. Perhaps the results can be manipulated to fit theory by using a more complex basis set? This was investigated at the B3LYP/6-31G* level with the three conformers that are very close to the minimum energy; gauche3, anti1 and anti2.

Table 11: Optimisation Summary Table of 1,5-Hexadiene Conformers at the B3LYP/6-31G* Level of Theory

Conformer	Structure	Newman Projection	Point Group	Total Energy/Hartrees B3LYP/6-31G*	Relative Energy kcal mol-1	Optimisation Files	Total Energy/Hartrees HF/3-21G	Relative Energy kcal mol-1
gauche3			C1	-234.61132934	0.30	DOI:10042/23109	-231.69266121	0.00
anti1			C2	-234.61180037	0.00	DOI:10042/23106	-231.69260220	0.04
anti2			Ci	-234.61170273	0.06	DOI:10042/23107	-231.69253516	0.08

At the B3LYP/6-31G* level of theory, the positioning of the gauche3, anti1 and anti2 relative energies has changed. Now, both antiperiplanar conformations are lower in energy than the gauche, in line with theory. The total energy for each B3LYP/6-31G* optimised molecule is lower than that of the corresponding HF/3-21G optimisation, but this does not mean that the former are "more stable"; total energy across basis sets can never be compared directly.

The anti1 conformation is now the most stable, being lower in energy than the anti2 by 0.0001 Ha, a much larger amount than the 0.00006 Ha difference between gauche3 and anti1 using the HF/3-21G basis set. An NBO analysis was run again on the gauche3 and anti2 conformations to investigate whether the stabilising π-π interactions are still present in gauche3.

Table 12: Comparison of HOMOs for anti2 and gauche3 Conformations

anti2 HOMO (B3LYP/6-31G*)	gauche3 HOMO (B3LYP/6-31G*)
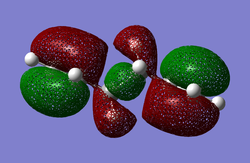DOI:10042/23113	DOI:10042/23112

The two resulting HOMO orbitals look very similar in appearance to the corresponding HF/3-21G HOMO anti2 and gauche3 orbitals. This shows that the change in relative conformational energies between these basis sets is due to the orbital overlap and Pauli repulsion antiperiplanar-favouring effects overriding the gauche-favoured through-space dispersion effect.

Structural Comparison Between Basis Sets

Though energies cannot be directly compared across basis sets, information concerning the structure of a molecule, such as bond angles and bond lengths, can. Table 13 summarises the key internuclear distances and dihedral angles of the anti2 conformation.

Table 13: Structural Comparison of Optimised 1,5-Hexadiene Between Basis Sets

Conformer	C2-C3-C4-C5 Dihedral Angle (°)	H-C3-C4-H Dihedral Angle (°)	C4-C3-C2=C1 Dihedral Angle (°)	C3-C4 Bond Length (Å)	C1=C2 Bond Lengths (Å)
Anti2 (HF/3-21G)	180.00	180.00	114.63	1.55	1.32
Anti2 (B3LYP/6-31G*)	180.00	180.00	118.53	1.55	1.33

What can be seen are very consistent results using the two basis sets. Using the correcr level of theory in computational analysis is vital for the retrieval of accurate results. The bond lengths and dihedral angles for the conformers of 1,5-hexadiene are accurate using both HF/3-21G and B3LYP/6-31G* levels of theory, but the two are not "interchangeable" when considering relative energy.

Frequency Analysis of 1,5-hexadiene

By showing that the negative gradient of the potential energy slope is zero only tells us that a staionary point on the potential energy surface has been reached. To ensure that the stationary point that has been found is a minimum, the second derivative of this slope needs to be taken. If the value is positive, a local minimum has been reached due to the upwards curvature of the gradient either side of the stationary point.

Frequency analysis is essentially the second derivative of the potential energy surface. If all frequencies are positive, then a minimum has been reached. Frequency analysis was carried out on the B3LYP/6-31G* optimised molecules of 1,5-hexadiene in the anti1, anti2 and gauche3 conformations.

Figure 5: Simulated infrared spectrum of anti2 conformer of 1,5-hexadiene

Figure 5 shows how the frequency analysis can be visualised for the anti2 conformer in the form of a simulated infrared spectrum. The lower energy vibrational modes around 1000cm^-1 correspond to bending motions of the molecule whereas relatively high energy bond stretching creates peaks in the 3000-3500cm^-1 region. All the calculated frequencies are real and positive, indicating a minimum was found on the potential energy surface.

As well as indicating that a minimum was reached, vibrational analysis allows important thermochemical data to be extracted. The three conformers also underwent frequency analysis at 0K. This was done by modifying the input file manually for a temperature of 0K and pressure of 1atm. The results from all frequency operations are displayed in the table below.

Table 14: Thermochemical Analysis of 1,5-Hexadiene Conformers with Varying Temperature

	Anti1 Thermochemistry
Temperature (K)	Sum of Electronic and Zero Point Energies (Hatrees)	Sum of Electronic and Thermal Energies (Hatrees)	Sum of Electronic and Thermal Enthalpies (Hatrees)	Sum of Electronic and Thermal Free Energies (Hatrees)	Link to Frequency Files
298.15	-234.469286	-234.461965	-234.461021	-234.500162	DOI:10042/23135
0	-234.469286	-234.469286	-234.469286	-234.469286	DOI:10042/23134
	Anti2 Thermochemistry
Temperature (K)	Sum of Electronic and Zero Point Energies (Hatrees)	Sum of Electronic and Thermal Energies (Hatrees)	Sum of Electronic and Thermal Enthalpies (Hatrees)	Sum of Electronic and Thermal Free Energies (Hatrees)	Link to Frequency Files
298.15	-234.469212	-234.461856	-234.460912	-234.500822	DOI:10042/23139
0	-234.469212	-234.469212	-234.469212	-234.469212	DOI:10042/23136
	Gauche3 Thermochemistry
Temperature (K)	Sum of Electronic and Zero Point Energies (Hatrees)	Sum of Electronic and Thermal Energies (Hatrees)	Sum of Electronic and Thermal Enthalpies (Hatrees)	Sum of Electronic and Thermal Free Energies (Hatrees)	Link to Frequency Files
298.15	-234.468693	-234.461464	-234.460520	-234.500105	DOI:10042/23137
0	-234.468693	-234.468693	-234.468693	-234.468693	DOI:10042/23138

The thermochemical analysis shows that the sum of the zero point energies (E = E_elec + ZPE) is not temperature dependent. This makes sense as this is defined as the potential energy at 0K (including zero-point vibrational energy). As temperature increases away from absolute zero, the sum of the electronic and thermal energies also increase due to the energy going into translational, vibrational and rotational modes (E = E + E_vib + E_trans + E_rot). Entropy also increases with increasing temperature, so the sum of the electronic and thermal enthalpies also increase. This result contains an additional correction of RT (H = E + RT). Finally, when the entropic contribution is considered (G = H - TS) the sum of electronic and thermal free energies decreases relative to that at absolute zero, again due to increases in entropy from the entropic extreme of absolute zero. The fact that the latter three of these energy values are equal to the sum of the electronic and zero-point energies show thermal dependence of these quantities.

Optimising the Chair and Boat Transition Structures

This section will focus on optimising and analysing both chair and boat transition structures of 1,5-hexadiene undergoing the Cope rearrangement. A transition state is a local maximum along the potential energy surface, meaning it is relatively unstable molecule that cannot be observed experimentally. An imaginary frequency is observed upon frequency analysis due to their negative force constant. Under the harmonic oscillator model, the relationship between force constant and frequency (cm^-1) can be represented as follows:

$\overline{\nu }=\frac{1}{2\pi c}\sqrt{\frac{k}{\mu }}$

A negative force constant (k) implies a negative square root value for the corresponding frequency, resulting in an imaginary number and hence imaginary frequency.

Chair

The chair transition structure can be optimised by thinking of it as two allyl fragments (CH₂CHCH₂). An allyl fragment was optimised at the HF/3-21G level of theory (DOI:10042/23157 ) and replicated in the Gaussview™ window so that they can be oriented in a way that mimics the chair transition structure, known as a "guess structure". The distance between the terminal carbon atoms between the two fragments was set to 2.2Å, which is the molecular bond breaking/formation distance.

Two methods can now be used to result in an optimised chair transition structure. If the guess structure was significantly close to the true transition structure of maximum energy, the force constant matrix method can be applied, in which the Hessian is computed in the first step of the optimisation and then updated as the optimisation progresses. If the guess structure isn't as accurate, then this approach may not work. Sometimes a better transition structure can be created by freezing the reaction coordinate (keyword: Opt=ModRedundant) and minimising the rest of the molecule. When the molecule is fully relaxed, the reaction coordinate can be unfrozen and the transition state optimisation started again. This is called the frozen coordinate method.

The table below compares the optimisations of the chair transition state using these two methods. For the force constant matrix approach, an additional keyword of "Opt=NoEigen" was required so that the calculation didn't terminate if two imaginary frequencies were found.

Table 15: Optimisations of 1,5-Hexadiene Cope Rearrangement Chair Transition State with Varying Method

Method	Point Group	Imaginary Frequency (cm-1)	Image of Imaginary Frequency	Optimized Bond Forming/Breaking Separation Distance (Å)	Total Energy of TS (Ha)	Optimisation Files
HF/3-21G (Force Constant Matrix)	C2h	-817.94		2.02	-231.61932247	DOI:10042/23160
HF/3-21G (Frozen Coordinates)	C2h	-818.03		2.02	-231.61932196	DOI:10042/23163 DOI:10042/23164

In this case it is evident that the method used doesn't affect the optimisation results. One negative imaginary frequency was present with each method, indicative of transition structures. The imaginary frequency is the same to the nearest whole wavenumber and the optimised bond formation/breaking bond lengths are identical when comparing the two methods. The imaginary frequency images in table 15 look like the Cope rearrangement.

Boat

To optimise the boat transition structure, the QST2 method needs to be applied to the 1,5-hexadiene molecule. This works by analysing the reactants and products of a reaction, interpolating between the two structures to find a transition state between them. This means that it is vital to number the reactants and products in the same way, as carbon atoms will be rearranged relative to their starting position after the rearrangement process.

The previously optimised HF/3-21G anti2 conformer of C_i symmetry was used and numbered carefully, before optimisation began at the same level of theory. The optimised molecule did not adopt boat structure using this QST2 approach, but rather a dissociated chair structure (shown in table 16). This is due to the process not taking rotational about bonds into account, simply translating the top fragment below itself. This means that these conformations of the product and reactant will never suffice to converge to the boat transition state.

The calculation was run again using a central C2-C3-C4-C5 dihedral angle of 0° followed by C2-C3-C4 and C3-C4-C5 angles of 100°. This makes the current conformation closer to the boat structure than the previous calculation. The optimisation and frequency analysis was run again at the same level of theory (HF/3-21G), this time converging to the desired boat transition state also shown in table 16. One imaginary frequency of -840.01cm^-1 was observed.

Table 16: Optimisations of 1,5-Hexadiene Cope Rearrangement Boat Transition State with Varying Method

Method	Image of Optimised Structure	Point Group	Imaginary Frequency (cm-1)	Image of Imaginary Frequency	Optimized Bond Forming/Breaking Separation Distance (Å)	Total Energy of TS (Ha)	Optimisation Files
HF/3-21G (QST2 - Optimisation 1)		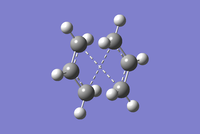C2h	N/A	N/A	2.02	N/A	DOI:10042/23165
HF/3-21G (QST2 - Optimisation 2)		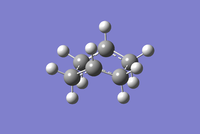C2v	-840.01		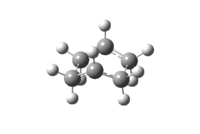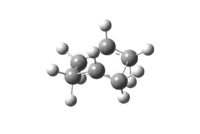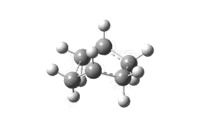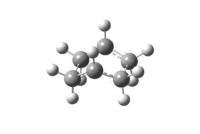2.14	-231.60280197	DOI:10042/23166

Comparison of Chair and Boat Transition States

The first thing that is obvious when comparing the chair transition structure to the boat is the energy difference. The chair has a total energy of -231.619322 Ha whilst the boat's energy is -231.602802 Ha (the energy difference of 0.01652 Ha corresponding to around 10 kcal mol^-1). The boat transition structure is higher in energy than the chair due to the steric clashes that occur as a result of its eclipsed conformation of C-H and C-C bonds, absent from the staggered chair orientation. These energies can be directly compared because the same level of theory was used with the same number of atoms.

The internuclear distances of the bonds being broken and formed are also in line with the energy difference; the boat transition state's 2.14A being longer than the chair's 2.02A (longer bonds implying weaker interaction). The lower imaginary vibrational frequency of the boat orientation (-840cm^-1 compared with -818cm^-1) also suggests a weaker bond.

Finally, the symmetry between the two transition states is also in line with the expected chair and boat point groups of C_2h and C_2v respectively.

Intrinsic Reaction Coordinate (IRC)

The structures of the boat and chair transition states have been analysed. It is now time to see which conformers of 1,5-hexadiene these transition structures connect. To do this, the intrinsic reaction coodinate needs to be followed throughout the reaction, which is the minimum energy path from a transition structure down to its local minimum on a potential energy surface. This creates a series of data points, a result of taking small steps in the direction of the steepest slope on the potential energy surface. Table 17 shows the results of IRC calculations on the frozen-coordinate optimised chair transition structure along with the optimised boat.

The reaction coordinate is symmetrical and so the IRC calculation computed in the forward direction only. The force constants were set to be calculated at every step and the number of steps set to N=50. An HF/3-21G level of theory was once again used.

Table 17: Intrinsic Reaction Coordinate for Chair and Boat Transition Structures ( HF/3-21G)

TS	Final IRC Structure	Energy Graph	Minimum Energy (Ha)	Gradient Graph	Gradient	IRC Files
Chair (N=50)			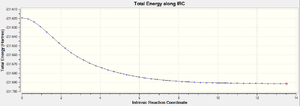-231.69157846		0.00015228	DOI:10042/23201
Boat (N=100)			-231.69262309		0.00013144	DOI:10042/23215

The gradient for the chair IRC calculation is low, but the final energy of the 1,5-hexadiene conformation doesn't correspond to any conformers in table 9. This suggests that the structure hasn't been sufficiently minimised and that the gradient can become even smaller. This molecule underwent an optimisation to a minimum at the HF/3-21G level of theory (DOI:10042/23200 ). The energy of this reoptimised conformation is -231.69166702 Ha, in direct agreement with the gauche2 conformer energy.

An N=100 IRC method was used with the boat as an N=50 method did not reach a satisfactory low value. This was successful, as the energy of -231.69266121 Ha after optimisation (DOI:10042/23216 ) is in excellent agreement with the most stable conformer of 1,5-hexadiene; gauche3.

Reoptimising at a Higher Level of Theory

Both chair and boat transition structures were reoptimised at the higher B3LYP/6-31G* level of theory. The energies cannot be compared between the two basis sets but can be compared between chair and boat with the same basis set.

The table below summarises the reoptimisation results.

Table 18: Energy Values Between Chair and Boat Transition Structures with Varying Level of Theory and Temperature

	Energy values
	HF/3-21G			B3LYP/6-31G*
	Electronic energy / Hatrees	Sum of electronic and zero-point energies/ Hatrees	Sum of electronic and thermal energies/ Hatrees	Electronic energy / Hatrees	Sum of electronic and zero-point energies / Hatrees	Sum of electronic and thermal energies/ Hatrees
		0 K	298.15 K		0 K	298.15 K
Chair Transition State	-231.61932	-231.46670	-231.46134	-234.55698	-234.41493	-234.40901
Boat Transition State	-231.60280	-231.45093	-231.44530	-234.54309	-234.40234	-234.39601
Anti 2 Conformer (Reactant)	-231.69254	-231.53954	-231.53257	-234.61170	-234.46921	-234.46186

From this information the activation energies for each method and transition state can be calculated by taking the difference in energy of the reactant and transition state. These are shown next to the experimental values.

Table 19: Activation Energies of Chair and Boat Transition Structures with Varying Level of Theory

	Activation energies
Method	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Literature
Temperature	0 K	298.15 K	0 K	298.15 K
Chair Activation Energy (kcal/mol)	45.70	44.69	34.06	33.16	33.5 ± 0.5
Boat Activation Energy (kcal/mol)	55.60	54.76	41.96	41.32	44.7 ± 2.0

Both levels of theory suggest that the chair is the lowest energy transition structure. The energy difference between the B3LYP/6-31G* and HF/3-21G levels of theory is rather large, but these cannot be compared directly (as in, the optimisation results for B3LYP/6-31G* cannot be classed as "more stable"). The experimental value for the activation energy is found to be +33.5 kcal mol^-1, corresponding closely to the chair transition structure transition energy. The experimental data are much closer to the B3LYP/6-31G* calculations for activation energy, whch is expected as it is a higher level of theory.

The Diels-Alder [4+2] Cycloaddition

Figure 6: Overview of the Diels-Alder cycloaddition mechanism

The Diels-Alder reaction is an extremely powerful reaction between a conjugated diene and a dienophile (an alkene or alkyne) to form closed-ring alkenes. It is a cycloaddition of pericyclic [_π4_s + _π2_s] nature, driven by the overall formation of two C-C σ-bonds at the expense of two weaker C=C π-bonds. These reactions are reversible and proceed with the supply of thermal energy (the backwards reaction being known as a retro-Diels-Alder reaction). A variant of this reaction in which carbon is replaced with other atoms such as nitrogen is called a hetero-Diels-Alder reaction, a very powerful way to synthesise six-membered heterocycles.

Background Theory

Before computationally simulating Diels-Alder reactions, some theory into the mechanistic process will be presented first so that a more thorough analysis of the results could follow.

The General Stereochemistry of Diels-Alder Reactions

Figure 7: General theoretical TS of a Diels-Alder reaction (no sym.).

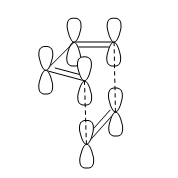
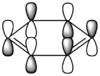
The most simple Diels-Alder cycloaddition reaction is that between butadiene and ethene, shown in figure 6. During the course of the pericyclic reaction, the p-orbitals of the diene form σ-bonds with the p-orbitals of the dienophile to result in stable six-membered ring formation. A way in which this could happen is a head-on approach of the diene towards the dienophile, represented without considering orbital symmetry in figure 7.

The proposed direction of attack and hence transition state of the reaction when this head-on approach is considered shows suprafacial bond formation for both diene and dienophile components. This isn't surprising as a very long flexible conjugated dienophile would be required to even make the possibility of the diene acting as an antarafacial component remote.

Another restraint in the Diels-Alder reaction is the need for the diene to adopt the s-cis conformation to give stable six-membered rings upon heating with the dienophile. If the diene reacted in the s-trans conformation, an impossibly high energy trans- double bond would have to be incorporated into the cyclohexene product. The s-trans form of butadiene is lower in energy than the s-cis form (~1% of butadiene molecules are in the s-cis conformation at room temperature), meaning cyclic dienes on the whole are much more reactive in Diels-Alder reactions as the energy difference between the s-trans and s-cis conformations does not have to be added to the activation energy.

Experimental Findings

Figure 8: The effects of adding a methoxy electron donating group onto the diene in a Diels-Alder cycloaddition on reaction rate.

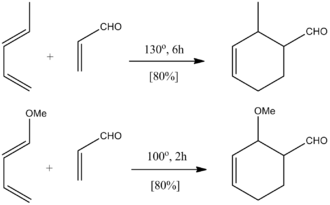
Experimental evidence shows that Diels-Alder reactions are much more likely to take place when electron withdrawing groups (e.g. nitro, nitrile, carbonyl, sulfonyl...) are added to the dienophile and electron donating substituents (amino, alkoxy, mehtyl...) added to the diene. It is possible to have electron donating groups on the dienophile if strong electron withdrawing groups are placed on the diene (an inverse electron demand), but these reactions have been found to not be as efficient. Figure 8 shows how lower temperatures and reaction times can be used when the electron-donating methoxy group is added to butadiene relative its unsubstituted counterpart to achieve equal yield, suggesting a more favoured reaction.

Stereochemistry

The Woodward-Hoffmann Rules

To explain the experimental observations, Roald Hoffmann added to a publication in 1965 by Robert Woodward that explained the stereospecificity of electrocyclic ring opening at the termini of conjugated open chained polyenes. This prompted much stereospecificity interest in other reaction mechanisms such as the Diels-Alder cycloaddition.

Figure 9: LCAO of Diels-Alder transition state.

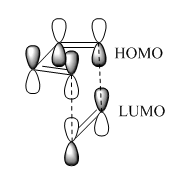
For the reaction to take place, the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) of the diene and dienophile have to interact with one another favourably. As the experimental evidence suggests adding electron donating groups to the diene results in lower reaction rates, the diene can be considered a 'nucleophile'. This means that the HOMO of this species will interact with the LUMO of the 'electrophilic' dienophile.

Butadiene contains four valence π-electrons, whereas ethene contains two. The linear combination of atomic orbitals were drawn so that the suprafacial interaction could then be visualised between the two components (figure 9). The frontier orbitals between HOMO butadiene and LUMO ethene are of perfect symmetry for efficient suprafacial overlap, with ethene approaching the butadiene molecule from below. The overlap between p-orbitals is highly directional, so Diels-Alder reactions classically have large negative entropy changes.

For a ground-state thermal cycloaddition to be allowed, the total number of (4q+2)_s and (4r)_a components need to be odd. For a Diels-Alder reaction reaction, the two components are the π-orbitals of the diene (four electrons) and the π-orbital of the dienophile (two electrons). Both of these components are suprafacial, resulting in a total number of six "s" electrons. This number can be represented in the form (4q+2), and so the sum of the (4q+2)_s and (4r)_a, where q is an integer, is equal to one. As this is an odd number, the reaction is thermally allowed.

Computational Analysis of the Diels-Alder Transition Structure

To confirm that the frontier orbital approach explained by the Woodward-Hoffmann rules govern the reaction mechanism, each reactant will be optimised to a minimum and then combined before a second optimisation is run to yield a maximum on the potential energy surface (i.e. a transition state).

s-cis Butadiene and Ethene

Optimisation of Reactants

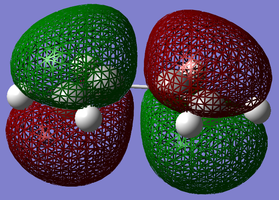
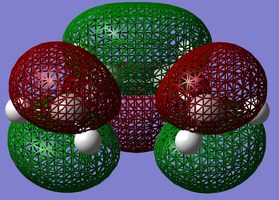
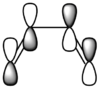
s-cis Butadiene was drawn in Gaussview™ and optimised at the Semi-Empirical/AM1 level of theory. The orbitals are labeled as either symmetric or anti-symmetric with respect to the plane between the central carbon atoms, perpendicular to the bond. LCAO images are placed below the visualised NBO, along with the optimisation file.

Table 20: s-cis Butadiene and Ethene Frontier Molecular Orbitals

Butadiene HOMO	Butadiene LUMO	Ethene HOMO	Ethene LUMO
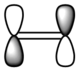Anti-symmetric	Symmetric	Symmetric	Anti-symmetric
DOI:10042/23219		DOI:[1]

For s-cis butadiene, the HOMO is an anti-symmetric molecular orbital with one nodal plane between the two central carbon atoms. The LUMO is a symmetric molecular orbital with two nodal planes between the two terminal C-C bonds. As the LUMO contains an extra nodal plane and hence an extra antibonding interaction, it is obvious why this is higher in energy.

The frontier orbitals for ethene are much less complicated, having a symmetric bonding π MO as the LUMO and an anti-symmetric antibonding π MO (with one perpendicular nodal plane) as the HOMO.

The results of this molecular orbital analysis show that symmetric-symmetric and asymmetric-asymmetric orbital interactions provide good overlap for a transition state to be formed (due to the similar symmetry forming favourable interactions). To investigate how the two components come together to form the transition structure, it will have to be drawn and optimised to a maximum.

Transition State Analysis

In order to optimise the transition state structure, the two previously optimised reactant molecules were opened in the same window of Gaussview™ and oriented in a way that mimics the bonding in the proposed transition state (the "guess structure"). The method used in this calculation is the frozen coordinate method, chosen because the terminal carbons are oriented based on a guess. As the force constant matrix method requires a structure very close to the transition state it loses appeal in this case and the frozen coordinate method wins out.

The transition state in the ethene/butadiene Diels-Alder reaction has an envelope structure to optimise the interaction between the π-orbitals of ethene and those of the conjugated butadiene system. The bond breakage/formation distance was set to 2.0Å and the terminal carbon coordinates frozen so that the rest of the molecule can be relaxed by carrying out a minimisation. A Semi-Empirical/AM1 level of theory was used involving no calculation of force constants during the optimisation. The coordinates were then unfrozen and an optimisation + frequency analysis run to identify a transition state (Berny). Force constants were set to 'calculate never' and a Semi-Empirical/AM1 level of theory used.

Table 21: Ethene and Butadiene Transition State Analysis (Semi-Empirical/AM1)

Image of Optimised Molecule	Frequency (cm-1)	Image of Frequency	Optimized Bond Lengths (Å)	Optimisation Files
	-956.12		Butadiene sp2: 1.38Å Butadiene sp3:1.40Å Ethene sp2: 1.38Å Formation/Breakage Separation: 2.12Å	DOI:10042/23231 DOI:10042/23268
	147.32		N/A	DOI:10042/23231 DOI:10042/23268

One negative imaginary frequency was observed at -956cm^-1, indicating a transition structure has been found. It can be seen from the vibrational analysis of the transition state that the ethene approaches butadiene and forms bonds in a concerted manner, as predicted. It is also worth notating the the ethene molecule approaches the butadiene molecule at an angle of 99.3 degrees, resulting in the "envelope transition structure" previously described.

The bond breakage/separation σ-C-C length was found to be equal 2.12Å for both all terminal carbon atoms between the intial components. This quantifies the observational analysis that the bonds are forming and breaking in a concerted manner at the transition state. The van der Waals radii of two carbon atoms combined is 3.40Å As the bond breakage/separation distance is smaller than this, it shows that the σ-bonds between the carbon atoms have not fully formed.

The C=C sp² bond length (1.38Å) is longer than the ethene C=C literature value of 1.34Å, implying that the ethene bond is being lengthened in the transition structure relative to its ethene starting length. This is in line with the concerted reaction mechanism where bond breakage of ethene is synchronous with the σ-bond formation of the ethene carbon atoms with butadiene.

The C-C sp³ single bond is shorter than the literature value of 1.54Å at the transition structure. This is because the single bond is on its way to becoming a double bond, strengthening it to become shorter, also indicative of the concerted nature of the transition state.

Table 19 also shows the first positive vibrational mode at 147cm^-1. The animation shows the terminal carbon atoms of butadiene and ethene bending towards and away from each other in an asynchronous fashion. The frequency is not the negative one as the transition state corresponds to synchronous bond formation and breakage.

Molecular Orbital Analysis

The molecular orbitals of the transition state between the two components were analysed.

Table 22: s-cis Butadiene and Ethene Transition State Molecular Orbitals

Transition State HOMO	Transition State LUMO
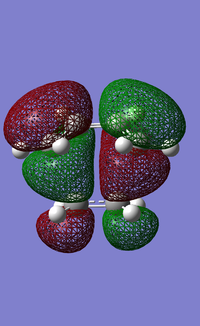Anti-symmetric	Symmetric
DOI:10042/23268

The results in table 20 show that the transition state frontier molecular orbitals consist of an anti-symmetric HOMO and a symmetric LUMO. The prediction was that the HOMO of butadiene (anti-symmetric) interacted with the LUMO of ethene (anti-symmetric) to produce the lowest energy fronteir orbital HOMO transition state (anti-symmetric). This is indeed what the analysis shows, also represented in LCAO form. Woodward and Hoffmann said that symmetry has to be preserved in the reaction plane before and after a pericylic reaction for it to be allowed. We have shown here that these rules are satisfied and so the reaction can proceed with the use of heat. The symmetric molecular orbital contributions to the LUMO of the transition state also satisfy the rule.

1,3-Cyclohexadiene and Maleic Anhydride

Scheme 2: The formation of endo and exo products from a regioselective Diels-Alder reaction.

A Diels-Alder reaction between 1,3-cyclohexadiene and maleic anhydride will now be investigated

Regioselectivity in the Diels-Alder Reaction

When more molecularly complex dienes and dienophiles are used in a Diels-Alder reaction, an issue of regiochemistry presents itself. The diene and dienophile can interact with the dienophile facing one of two ways, best described using an image (scheme 2).

The maleic acid molecule can react with 1,3-cyclohexadiene either with the C-O-C bond facing the C2-C3 bond in the diene or away from it. Two products are formed, called endo and exo.

The endo product is usually higher in energy than the exo due to the introduction of steric clashes between the C-C bond attached diirectly to C=C in the dienophile and the orbitals of the diene system.

Optimisation of Reactants

1,3-cyclohexadiene and maleic anhydride were drawn in Gaussview™ and optimised at the Semi-Empirical/AM1 level of theory. The orbitals are labeled as either symmetric or anti-symmetric with respect to the plane between the central carbon atoms, perpendicular to the bond. LCAO images are placed below the visualised NBO, along with the optimisation files.

Table 23: 1,3-Cyclohexadiene and Maleic Anhydride Frontier Molecular Orbitals

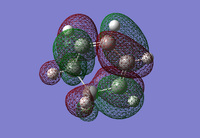
1,3-Cyclohexadiene HOMO	1,3-Cyclohexadiene LUMO	Maleic Anhydride HOMO	Maleic Anhydride LUMO
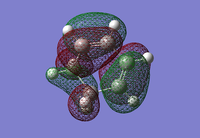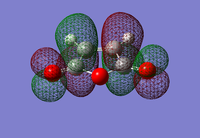Anti-symmetric	Symmetric	Symmetric	Anti-symmetric
DOI:10042/23277		DOI:10042/23278

Just like the previous Diels-Alder reaction that was optimised, the HOMO of the diene has the same anti-symmetric symmetry as the LUMO of the dienophile (maleic anhydride). The expection is that these can combine to form an anti-symmetric HOMO transition state. A transition state calculation will now be carried out to see if this is a correct statement to make.

Transition State Analysis

The transition state was first mimicked by creating both exo and endo products first. Two C-C bonds between the cyclohexadiene and maleic anhydride components were cleaved and placed 2.2Å away from each other, being careful to add double bonds in the correct places. A transition state (Berny) optimisation and frequency analysis were then carried out also at the Semi-Empirical/AM1 level of theory. The resulting optimised transition states are shown in table 21.

Table 24: Maleic Anhydride and 1,3-Cyclohexadiene Transition Structure Analysis

Molecule	Image of Optimised Molecule	Total Energy (Ha)	Imaginary Frequency (cm-1)	Image of Frequency	Optimized Formation/Breakage Bond Length (Å)	Optimisation Files
Exo		-0.05041984	-812.27		2.17	DOI:10042/23294
Endo		-0.05150480	-806.27		2.16	DOI:10042/23293

One imaginary frequency was found in each calculation, so a transition state has been achieved. The animations of the vibrations show the beginnings of a concerted formation of two new C-C σ-bonds at the overall expense of two C=C π-bonds.

Molecular Orbital Analysis

A surprising result is the lower energy endo transition state compared with the exo. When a reaction is under kinetic control, the thermodynamics of the products are irrelevant. The transition state that is the lowest in energy relative to another leads to the kinetic product. A molecular orbital analysis was carried out to see if this can be rationalised.

Table 25: Molecular Orbitals of Exo and Endo Transition States Between Maleic Anhydride and 1,3-Cyclohexadiene

Molecule	HOMO-1	HOMO	LUMO	LUMO+1
Exo
	Symmetric	Anti-symmetric	Anti-symmetric	Symmetric
Endo
	Symmetric	Anti-symmetric	Anti-symmetric	Symmetric

As predicted, the HOMOs of both endo and exo product are anti-symmetric, produced by the combination of the anti-symmetric 1,3-cyclohexadiene HOMO and the anti-symmetric maleic anhydride LUMO. Six electrons are involved in the bonding process and so the reaction is allowed thermally.

Why is the endo transition state lower energy by 0.680 kcal mol^-1 compared to the exo? This can be explained in two ways; one involving a frontier orbital approach and the other involving steric interactions. The latter of these two will be approached first.

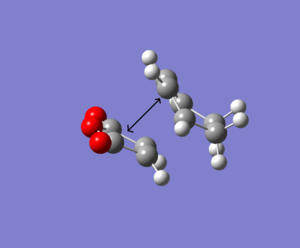
Steric Effects

The table below represents the exo and endo product so that the maleic anhydride is aligned in the same way.

Table 26: Steric Interactions Between Maleic Anhydride and 1,3-Cyclohexadiene Transtion Structure

Endo Product	Exo Product

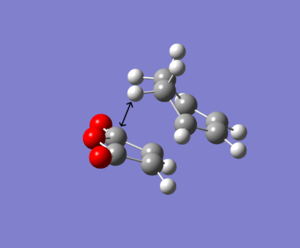In the exo product there is a steric clash with sp³ hybridised carbon. The hydrogen atom is directed towards the C-O-C bond (angle 106 degrees) at a distance below the carbon-carbon van der Waals radii of 3.40Å, resulting in a steric clash hence an increase in electronic energy. In the endo form, the carbons are sp² hybridised (at angle 90 degrees) and so the hydrogen atoms are perpendicular to the C-O-C, avoiding unfavourable steric clashes to lower the energy of the transition state. However, at higher levels of theory the optimisation may align the hydrogen atoms in a more energetically stable orientation.

Secondary Orbital Overlap

The secondary orbital overlap theory is a frontier orbital based theory that can explain why the endo transition state is lower in energy than the exo in this Diels-Alder reaction. If the dienophile contains π-orbitals not involved in the bond breakage/making steps that can be aligned towards the diene's orbitals (also not involved in bond making/breaking steps) then they can interact to stabilise the transition state.

Upon inspection of the HOMOs for both transition structures, no secondary orbital overlaps can be observed. However, a very obvious secondary orbital overlap can be visualied in both LUMO+1 molecular orbitals (table 25), represented by the diffuse red lobes between the two components from the C-O-C bond. An example of a secondary orbital overlap in the HOMO of the endo product, thought to be the reason of its stability, is shown below:

It is clear the computational chemistry has limitations of detecting secondary orbital overlaps in the frontier orbitals at this level of theory. Computational studies have found such interactions to be either non-exitent or extremely weak in nature for a thermal cycloaddition. Higher levels of theory might be able to detect them, or could it be that they do not exist and computational techniques at the B3LYP/6-31G* level of theory are accurate?

Conclusion

Chair and boat transition states of 1,5-hexadiene were successfully optimised at the B3LYP/6-31G* level of theory to result in activation energies of the literature activation energy for the Cope rearrangement (33.5 kcal mol^-1), in support of a concerted pericyclic sigmatropic rearrangement mechanism. Optimising at the B3LYP/6-31G* level of theory produced results 11 kcal mol^-1 closer to this literature value compared with a HF/3-21G method.

The Woodward-Hoffmann rules were satisfied after molecular orbital analysis for a range of diene and dienophiles, showing anti-symmetric symmetry-allowed thermal interactions between the HOMO of the diene and LUMO of the dienophile at the Semi-Empirical/AM1 level of theory. Regioselectivity was then explored, also at the Semi-Empirical/AM1 level of theory, to account for the lower energy endo product for the Diels-Alder reaction between 1,3-cyclohexadiene and maleic anhydride. A possible 'secondary frontier orbital overlap' of the transition state was suggested, though computational methods at this level of theory suggested a steric-based explanation.