Rep:Mod:db810

Bonding and Molecular Orbitals in Main Group Compounds

Inorganic Module 2

Abstract

Introduction to Computational Chemistry

Computational chemistry is the branch of chemistry that applies mathematical, chemical and computing techniques to solve chemical problems. It is a powerful technique that can be used to great effect when certain properties of molecules are required, ranging from electronic structure determinations to potential energy surface calculations. Acquiring such data enables the chemist to form predictions in relation to their reactions before experiments are run, making them better prepared for making observations.

The underlying foundation to all computational chemistry is the Schrödinger equation which can be greatly simplified by applying the Born-Oppenheimer approximation, allowing a wavefunction to be broken down into both electronic and nuclear vibrational and rotational parts. The electronic part of this equation is then solved for electrons only, assuming nuclei are fixed. This greatly reduces the complexity of the algorithms involved in the computational analysis and hence leads to shorter times for a simulated calculation to be made.

Having a large database of chemical compounds at your fingertips is incredible advantageous, especially when the materials under consideration:

• Are too expensive to purchase
• Impose serious health risks (e.g. toxicity, radioactivity)
• Are difficult to synthesise
• Aren't readily available

Optimising Molecules

Figure 1: Potential energy / distance graph for a diatomic molecule.

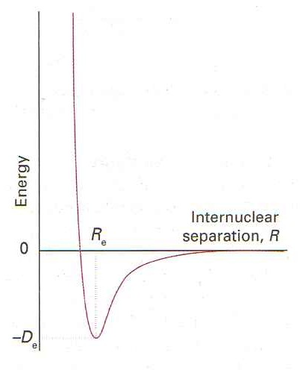
When the Born-Oppenheimer approximation is used on the Schrödinger equation, energy can be obtained as a function of the distance between the fixed nuclei. As the nuclei move closer together, favourable coulombic nuclear-electron interactions result in a decrease in the total energy until a point is reached where the nuclei begin to repel one another, resulting in a rapid increase in energy. This point is known as the equilibrium distance between nuclei and corresponds to a state where there is no force governing which way the nuclei will move relative to each other. For a diatomic, this is summarised in figure 1. This is the potential energy surface (PES) of the molecule and is what is used when carrying out an optimisation in a computational program such as Gaussian™.

From an initial predetermined internuclear distance, Gaussian™ changes this distance and calculates the difference in energy brought about by the change. The gradient at the point is also calculated to determine the force, where the force vector is the negative derivative of potential energy with respect to distance:

$\overrightarrow{F}=-\overrightarrow{\mathrm{\nabla }}U$

When a minimum in energy difference has been determined by sweeping through internuclear distances the gradient will equal zero; indicative of a stationary point and hence equilibrium distance. The length between nuclei in this stable equilibrium state is called the optimised bond distance.

Pseudo-Potentials

For lighter elements, the Schrödinger equation is sufficient to provide reliable results computationally. As the atoms increase in size and mass, relativity starts to affect the calculations which can provide results deviating from expectations.

A way around these relativistic effects is to use a "pseudo-potential" that represents the core electrons in a heavy atom as a function. Although there is an assumption made here that it is the valence electrons alone that determine bonding character, pseudo-potentials are surprisingly accurate.

Basis Sets

A basis set is the linear combination of atomic orbitals needed to define a group of functions to represent molecular orbitals.

When analysing post-second row atoms, where the atomic structure gets more complex, the basis set needs to be improved to describe the electronic structure more accurately. By improving the basis set, the time taken to optimise the molecule increases so there is discrepancy between high accuracy attained and a low CPU times.

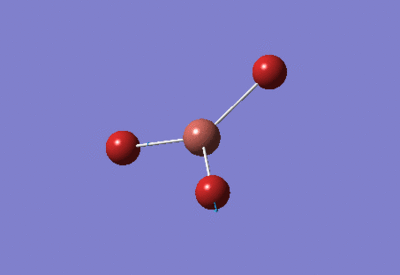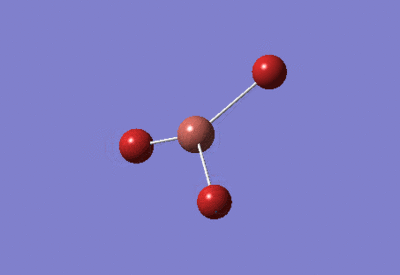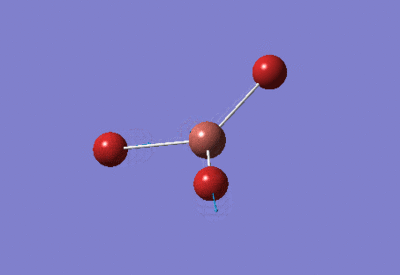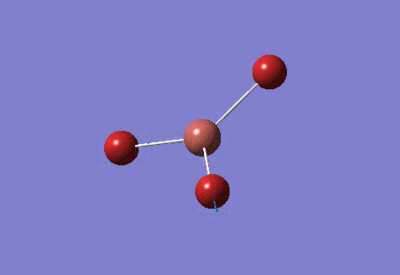
Optimising a Molecule of BH₃

Borane (BH₃) is a trigonal planar molecule with three sp² hybridised bonds and D_3h symmetry. Its vacant p orbital orthogonal to the σ_h plane gives it high Lewis acidity. Free borane is therefore only found in the gas phase as it can readily dimerise to diborane (B₂H₆).

3-21G Basis Set

Table 1

BH3 Optimisation: 3-21G Basis Set
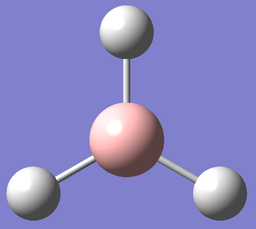
Optimised H-B-H bond angles: 120° Optimised B-H bond lengths: 1.19349Å
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	3-21G
Charge	0
E(RB3LYP)	-26.46226338 a.u.
RMS Gradient	0.00020672 a.u.
Dipole Moment	0.0000 Debye
Point Group	D3h
Job CPU Time	13.0 Seconds
link to .log file

A BH₃ molecule was drawn in GaussView™ (a graphical interface of Gaussian™) and an optimisation calculation was run with internuclear B-H distances set to 1.5Å using the low-accuracy 3-21G basis set, coupled with a B3LYP method.

The summary of the calculation and an image of the optimised molecule are displayed in table 1, which also includes the optimised bond lengths and angles.

Table 2

Item Table for BH3 Optimisation Using a 3-21G Basis Set

Item Value Threshold Converged? Maximum Force 0.000413 0.000450 YES RMS Force 0.000271 0.000300 YES Maximum Displacement 0.001610 0.001800 YES RMS Displacement 0.001054 0.001200 YES Predicted change in Energy=-1.071764D-06 Optimization completed. -- Stationary point found. ----------------------------  ! Optimized Parameters  !  ! (Angstroms and Degrees)  ! -------------------------- --------------------------  ! Name Definition Value Derivative Info.  ! --------------------------------------------------------------------------------  ! R1 R(1,2) 1.1935 -DE/DX = 0.0004  !  ! R2 R(1,3) 1.1935 -DE/DX = 0.0004  !  ! R3 R(1,4) 1.1935 -DE/DX = 0.0004  !  ! A1 A(2,1,3) 120.0 -DE/DX = 0.0  !  ! A2 A(2,1,4) 120.0 -DE/DX = 0.0  !  ! A3 A(3,1,4) 120.0 -DE/DX = 0.0  !  ! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0  ! ------------------------------------------------------------------------------- GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

Table 2 shows the Item table for the optimisation. It is clear from this that there was convergence within the calculation (note the "YES" characters within the table) and that a stationary point was found (note the -DE/DX values reaching 0.0). The optimised H-B-H angle of 120° (diborane lit 120.29) is consistent with trigonal planar geometry and the optimised bond distance of 1.19349Å in good agreement with literature (diborane terminal B-H distance = 1.1968Å)

The optimisation is also represented graphically below. It shows how both the total energy and the RMS gradient (force) change with each step of the optimisation before reaching minimum values.

Figure 2: Graphical representation of the optimisation of borane using the 3-21G basis set.

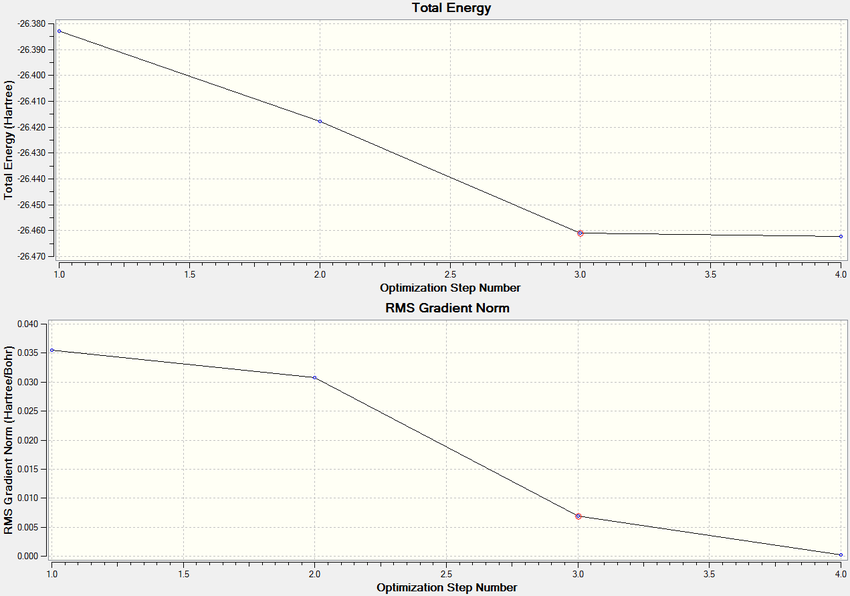
6-31G(d,p) Basis Set

Table 3

BH3 Optimisation: 6-31G(d,p) Basis Set
Optimised H-B-H bond angles: 120° Optimised B-H bond lengths: 1.19143Å
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
E(RB3LYP)	-26.61532252 a.u.
RMS Gradient	0.00021672 a.u.
Dipole Moment	0.0000 Debye
Point Group	D3h
Job CPU Time	11.0 Seconds
link to .log file

The previously optimised molecule was further optimised using the more complex 6-31G(d,p) basis set. Again, a B3LYP method was used. Table 3 summarises the optimisation, which also includes the optimised bond lengths and angles.

Table 4

Item Table for BH3 Optimisation Using a 6-31G(d,p) Basis Set

Item Value Threshold Converged? Maximum Force 0.000433 0.000450 YES RMS Force 0.000284 0.000300 YES Maximum Displacement 0.001702 0.001800 YES RMS Displacement 0.001114 0.001200 YES Predicted change in Energy=-1.189019D-06 Optimization completed. -- Stationary point found. ----------------------------  ! Optimized Parameters  !  ! (Angstroms and Degrees)  ! -------------------------- --------------------------  ! Name Definition Value Derivative Info.  ! --------------------------------------------------------------------------------  ! R1 R(1,2) 1.1914 -DE/DX = 0.0004  !  ! R2 R(1,3) 1.1914 -DE/DX = 0.0004  !  ! R3 R(1,4) 1.1914 -DE/DX = 0.0004  !  ! A1 A(2,1,3) 120.0 -DE/DX = 0.0  !  ! A2 A(2,1,4) 120.0 -DE/DX = 0.0  !  ! A3 A(3,1,4) 120.0 -DE/DX = 0.0  !  ! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0  ! -------------------------------------------------------------------------------- GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

Table 4 confirms that the series has indeed converged. The RMS gradient is also below 0.001, further indicating a convergence. An optimised H-B-H angle of 120° implies a trigonal planar coordination geometry.

It is not surprising to observe the smaller optimised B-H bond distance when the more complex ("better") basis set is used. The energy is also smaller with the 6-31G(d,p) basis set by a value of 0.15305914 a.u. This corresponds to 401.86 kJ/mol, a very large amount of energy considering the bonds are shortened by 0.00206Å! It is therefore important to note that energies of molecules over different basis sets (or pseudo-potentials) or molecules with different numbers of atoms cannot be compared. Only structures with the same number of atoms run with the same basis sets can directly be compared energetically as these values are highly dependent on basis set quality.

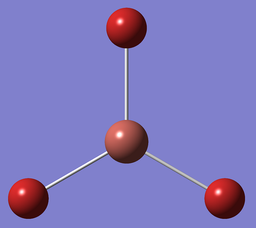
Optimising a Molecule of TlBr₃

Table 5

TlBr3 Optimisation: LanL2DZ Basis Set
Optimised Br-Tl-Br bond angles: 120° Optimised Tl-Br bond lengths: 2.65095Å
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	LanL2DZ
Charge	0
E(RB3LYP)	-91.21812851 a.u.
RMS Gradient	0.00000090 a.u.
Dipole Moment	0.0000 Debye
Point Group	D3h
Job CPU Time	39.7 Seconds
DOI:10042/22721

Thallium (III) bromide is a relatively unstable compound that disproportionates to thallium (II) bromide below 40°C.

LanL2DZ Basis Set

Thallium and bromine are both large atoms with many electrons in their structures; 81 and 35 respectively. A pseudo-potential is required to minimise effects arising from relativity. The medium-level LanL2DZ basis set is perfect for this type of calculation; it uses the D95V basis set for first row atoms and the Los Alamos ECP pseudo-potential on heavier elements.

The optimisation was carried out using a B3LYP method after restricting the geometry of the molecule to D_3h with a "very tight" tolerance to reduce errors in the calculation. This job was sent to Imperial's D-Space and a DOI link is provided in table 5.

Table 6

Item Table for TlBr3 Optimisation Using a LanL2DZ Basis Set

Item Value Threshold Converged? Maximum Force 0.000002 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000022 0.001800 YES RMS Displacement 0.000014 0.001200 YES Predicted change in Energy=-6.084036D-11 Optimization completed. -- Stationary point found. ----------------------------  ! Optimized Parameters  !  ! (Angstroms and Degrees)  ! -------------------------- --------------------------  ! Name Definition Value Derivative Info.  ! --------------------------------------------------------------------------------  ! R1 R(1,2) 2.651 -DE/DX = 0.0  !  ! R2 R(1,3) 2.651 -DE/DX = 0.0  !  ! R3 R(1,4) 2.651 -DE/DX = 0.0  !  ! A1 A(2,1,3) 120.0 -DE/DX = 0.0  !  ! A2 A(2,1,4) 120.0 -DE/DX = 0.0  !  ! A3 A(3,1,4) 120.0 -DE/DX = 0.0  !  ! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0  ! -------------------------------------------------------------------------------- GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

The Item table above shows that there was convergenge in force (-DE/DX). The optimised bond length of 2.65095Å is in agreement with literature (2.52Å) and the Br-Tl-Br optimised angle implies trigonal planar geometry.

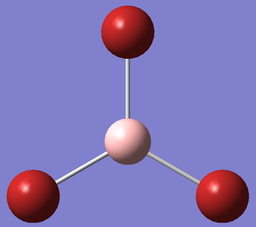
Optimising a Molecule of BBr₃

Table 7

BBr3 Optimisation: Gen Basis Set
Optimised Br-B-Br bond angles: 120° Optimised B-Br bond lengths: 1.93396Å
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	Gen
Charge	0
E(RB3LYP)	-64.43645296a.u.
RMS Gradient	0.00000382 a.u.
Dipole Moment	0.0000 Debye
Point Group	D3h
Job CPU Time	18.3 Seconds
DOI:10042/22805

Boron tribromide is a highly reactive fuming liquid at room temperature which has strong Lewis acid properties.

Gen Basis Set

In this case, there are both heavy and light atoms in the same molecule. A pseudo-potential would need to be applied for the bromine atoms whereas a full basis set for boron is needed. The Gen basis set allows the user to specify basis sets for individual atoms within a molecule. For this optimisation, a 6-31G(d,p) was used for boron and LanL2DZ for bromine with a RB3LYP method. The molecule was created using Gaussview™ with a modified molecule of optimised BH₃ shown in table 3.

Table 8

Item Table for BBr3 Optimisation Using a Gen Basis Set

Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000036 0.001800 YES RMS Displacement 0.000023 0.001200 YES Predicted change in Energy=-4.027671D-10 Optimization completed. -- Stationary point found. ----------------------------  ! Optimized Parameters  !  ! (Angstroms and Degrees)  ! -------------------------- --------------------------  ! Name Definition Value Derivative Info.  ! --------------------------------------------------------------------------------  ! R1 R(1,2) 1.934 -DE/DX = 0.0  !  ! R2 R(1,3) 1.934 -DE/DX = 0.0  !  ! R3 R(1,4) 1.934 -DE/DX = 0.0  !  ! A1 A(2,1,3) 120.0 -DE/DX = 0.0  !  ! A2 A(2,1,4) 120.0 -DE/DX = 0.0  !  ! A3 A(3,1,4) 120.0 -DE/DX = 0.0  !  ! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0  ! -------------------------------------------------------------------------------- GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

The optimised bond length of 1.93396Å is in good agreement with literature (1.89Å). The optimised Br-B-Br angle of 120 supports a trigonal planar geometry. The Item Table above indicates convergence, which is confirmed with the RMS gradient of 0.00000382 a.u. being much lower than 0.001 a.u.

Structure Comparison of BH₃, BBr₃ and TlBr₃

Table 9: Optimised Bond Length Summary

Bond	Bond Length (Å)
B-H	1.19143
B-Br	1.93396
Tl-Br	2.65095

Differences in Bond Length

Table 9 summarises the key bond distance results acquired from the optimisations discussed in the previous section. The B-H bond distance used here is that of the more complex basis set 6-31G(d,p).

When the ligand is changed from hydrogen to bromine with boron as a central atom, the bond length increases. Both hydrogen and bromine are available to donate electrons to form bonds, but a main difference between the two is that hydrogen donates an electron in its 1s orbital whereas bromine donates an electron from a 4p orbital. Though p orbitals in general are more directional than isotropic s orbitals to provide better overlap for electron sharing, the difference in principal quantum number between 4p and the 2sp² orbitals of boron is too large to provide efficient overlap. The stronger overlap with 1s hydrogen is more favourable energetically, which corresponds to a shorter bond length; a difference of 0.74253Å when compared with bromine 4p.

The same principle governs the effects of changing the central atom. Though boron and thallium are both in group 3, the sp² hybridised orbitals of boron used for bonding have a principle quantum number of 2 compared with thallium's 6. Bromine's 4p orbital overlap is much better with 2sp² bromine compared with 6sp² thallium due to the less diffuse nature of this hybridised boron orbital.

Bonding: A Definition

A bond is defined as an interaction between two atoms, whether it being an electrostatic attraction between two ions (i.e. an ionic bond) or an interatomic sharing of electrons between orbitals (a covalent bond). A region of high electron density is found between these two atoms. It is rare to observe solely one type of bonding in an interaction between two different atoms due to small changes in electronegativity shifting the electron density towards one atom. 100% covalence implies full electron density precisely half way between two interacting nuclei.

During certain points in the optimisation of a molecule in Gaussian™, Gaussview™ shows that bonds are not drawn between the atoms. Gaussview™ has predefined values as to what a bond is (perhaps referenced average bond lengths ± a certain value). When the interatomic distance falls into this predefined threshold, bonds are drawn.

Frequency Analysis

BH₃

Table 10: BH₃ Frequency 6-31G(d,p)

File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31(d,p)
Charge	0
E(RB3LYP)	-26.61532364 a.u.
RMS Gradient Norm	0.00000162 a.u.
Dipole Moment	0.0000 Debye
Point Group	D3h
Job CPU Time	8.0 Seconds
link to .log file

Frequency analysis is essential to support the idea that the optimised molecule lies at an energy minimum and is the most stable structure.

The 6-31G(d,p) optimised molecule of borane underwent frequency analysis. The same basis set and the same method must be applied here for the results to be meaningful, so the frequency analysis was done under a 6-31G(d,p) basis set and R3LYP method. The command "int=grid=ultrafine" was inputted as an additional keyword to reduce the noise by reducing the range of electron density. A "very tight" D_3h point group constraint also needed to be applied to reduce low frequency magnitude to provide more meaningful data. Table 10 summarises the frequency analysis on the optimised borane molecule.

Table 11

Item Table for BH3 Frequency Analysis Using a 6-31G(d,p) Basis Set
Low frequencies --- -7.0794 -7.0439 -0.0279 0.0004 0.7084 6.6303 Low frequencies --- 1163.0023 1213.1577 1213.1579

The energy of the molecule after the frequency analysis is similar to that of the optimised borane using the 6-31(d,p) basis set. This indicates that the frequency analysis was a success and that the molecule was minimised. The low frequencies quoted in table 11 are within ±15 cm^-1 which indicates that the motions of the molecule's centre of mass do not significantly interfere with the frequencies we wish to analyse; the first vibration has A2" symmetry and a frequency of 1163.0023 cm^-1 which is just under 165 times the value of the highest low frequency. These six low vibrational frequencies should be as close to zero as possible for the best result frequency analysis.

A non-linear molecule has 3N-6 modes of vibration. The low frequencies represent the "-6" part of the equation, so for a 4 atom molecule such as borane there are 6 vibrational modes that can be visualised. These vibrations are represented in table 12.

Table 12: Vibrational Modes of Borane

Number	Form of Vibration	Frequency (cm-1)	Intensity	Symmetry (D3h Point Group)
1	All 3 hydrogen atoms bend up and down away from the σh plane in a concerted fashion, opposite to the direction to the moving boron atom.	1163.00	92.5654	A"2
2	Two hydrogen atoms rock side to side with whilst another rocks opposite to this motion. The boron atom also moves in the same plane.	1213.16	14.0563	E'
3	Two hydrogen atoms scissor towards eachother whilst the boron and third hydrogen atom bounce in the same plane with no stretching of the bond.	1213.16	14.0557	E'
4	All hydrogen atoms move in and out together in a concerted motion whilst the B atom is stationary. There is no change in dipole moment.	2582.48	0.0000	A'1
5	Two hydrogen atoms stretch away from one another whilst the third is stationary. The boron atom moves towards each bending hydrogen atom in turn.	2715.61	126.3354	E'
6	Two hydrogen atoms stretch with synchronicity towards the boron atom as it moves towards them. The other hydrogen atom stretches towards the boron as the other two hydrogens are stretching away.	2715.61	126.3294	E'

Infrared Spectrum of BH₃

Figure 3: Simulated infrared spectrum of borane.

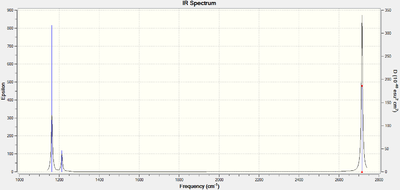
The infrared spectrum of borane can be simulated using the Gaussview™ interface and is shown in figure 3 below.

The spectrum clearly shows three infrared peaks centred around 1163cm^-1, 1213cm^-1 and 2716cm^-1 even though there are six vibrational modes for the molecule. This is because vibrational mode 4 corresponding to a frequency of 2582.48cm^-1 is totally symmetric and results in no change in the dipole moment of the molecule, rendering it IR inactive. Modes 5 and 6 are degenerate with E' symmetry, as are 2 and 3. Degeneracy means that both sets of vibrations correspond to one frequency each because equal energy implies equal frequency under the Planck relation.

The final result is an infrared spectrum comprising of peaks at 1163.00cm^-1, 1213.16cm^-1 and 2715.61cm^-1. These values are consistent with literature, where BH₃ was successfully trapped by the pyrolysis of BH₃CO in Ar matrix to produce infrared peaks at 1125, 1604 and 2808cm^-1.

TlBr₃

A frequency analysis was also run on the previously optimised TlBr₃. The frequency analysis was run with the LanL2DZ basis set, which uses pseudo-potential to model the core electrons as both thallium and bromine are large molecules that experience relativistic effects. Again, a RB3LYP method was used:

Table 14

Item Table for TlBr3 Frequency Analysis Using a LANL2DZ Basis Set
Low frequencies --- -0.0012 -0.0006 0.0000 1.8732 2.6580 2.6580 Low frequencies --- 46.6999 46.7000 51.9500

Table 13: TlBr₃ Frequency Summary (LANL2DZ)

File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Charge	0
E(RB3LYP)	-91.21813024 a.u.
RMS Gradient Norm	0.00000000 a.u.
Dipole Moment	0.0000 Debye
Point Group	D3h
Job CPU Time	36.7 Seconds
DOI:10042/22819

All of the low frequencies are within the range of ±15cm^-1. Each frequency is also positive and much larger than the highest low frequency, which indicates that a minimum has been found in the analysis. The table below shows the values of the low frequencies. The simulated infrared graph shows 3 peaks due to one of the TlBr₃ vibrational modes being IR inactive due to a totally symmetric stretch resulting in no change in dipole moment and four of the six being two degenerate pairs.

Table 15: Vibrational Modes of Thallium Tribromide

Number	Form of Vibration	Frequency (cm-1)	Intensity	Symmetry (D3h Point Group)
1	Scissoring of two hydrogen atoms in-plane.	46.70	3.6815	E'
2	Asymmetric scissoring of three hydrogen atoms.	46.70	3.6815	E'
3	All three hydrogen atoms bend in and out of the sigmah plane.	51.95	5.8464	A"2
4	All hydrogen atoms move in and out together in a concerted motion whilst the thallium atom is stationary. There is no change in dipole moment.	165.27	0.0000	A'1
5	In-plane assymmetric stretch of two hydrogen atoms.	210.75	25.4731	E'
6	In-plane asymmetric stretch of three hydrogen atoms.	210.75	25.4732	E'

Infrared Spectrum of TlBr₃

Figure 4: Simulated infrared spectrum of thallium (III) bromide.

The simulated infrared graph shows 3 peaks (46.7, 51.95 and 210.75cm^-1) because one of the TlBr₃ vibrational modes is IR inactive due to a totally symmetric A'₁ stretch resulting in no change in dipole moment. Four of the six modes are two degenerate pairs; similar to that of the borane infrared spectrum. Two of these peaks were observed in literature (60cm^-1 and 215cm^-1)

Differences Between BH₃ and TlBr₃

One of the most striking differences are the values in stretching frequencies between similar symmetry labels and the ordering of these labels (table X). In TlBr3, two degenerate bending modes of E' symmetry are lowest in energy, 46.70cm^-1 compared with borane's 1163.00cm^-1 lowest energy A"₂ mode. The A"₂ symmetry vibrational mode in TlBr₃ is much lower at 51.95cm^-1. As Thallium and bromine are both large atoms, the reduced mass (μ) of the molecule will be relatively large compared with borane. The issue of comparatively weak overlap within TlBr₃ discussed earlier also weakens the force constant (k) within the bond when the vibration is treated as a quantum harmonic oscillator. Using this model, the frequency of the vibrational mode can be calculated using the following equation:

$\overline{\nu }=\frac{1}{2\pi c}\sqrt{\frac{k}{\mu }}$

Table 16: Vibrational Modes by Symmetry Label

Symmetry Label	BH3 (cm-1)	TlBr3 (cm-1)
A"2	1163.00	51.95
E'	1213.16	46.70
A'1	2582.48	165.27
E'	2715.61	210.75

The reciprocal relationship between the vibrational stretching frequency and the reduced mass of the molecule is consistent with the findings from the simulated infrared spectrum. As the force constant increases (i.e. the bond gets stronger) the frequency of the vibrational mode also increases which is represented by the above equation.

It is also worth noting the differences in frequency between symmetry labels also. The lower energy vibrational modes (A"₂ and the first set of degenerate E') are bending modes whereas the higher frequency A'₁ and E' modes are stretches. This is the case because stretching affects the potential energy (and hence frequency) by altering internuclear distances in bonds (as figure 1 depicts) to a much larger extent than simply altering geometry through bending.

Population Analysis of BH₃

Population analysis was carried out on optimised borane by adding the phrase "pop=full" to the calculation. The below diagram represents the results of the analysis in the form of a molecular orbital diagram. Linear combination of atomic orbitals and the simulated orbitals are shown together. A 6-31G(d,p) basis set was used and the analysis was published to D-space: DOI:10042/22820

Figure 5: Molecular orbital diagram of borane

NBO Analysis of NH₃

An NBO analysis will now be carried out on a molecule of ammonia. Ammonia is a compound containing nitrogen and hydrogen and is a gas at room temperature. It has a characteristic pungent smell and is incredibly versatile amongst all disciplines of chemistry; being the building block of a huge range of pharmaceuticals.

Optimising a molecule of NH₃

Table 17

NH3 Optimisation: 6-31G(d,p) Basis Set
Optimised H-N-H bond angles: 105.748° Optimised N-H bond lengths: 1.01797Å
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
E(RB3LYP)	-56.55776856 a.u.
RMS Gradient	0.00000885 a.u.
Dipole Moment	1.8464 Debye
Point Group	C1
Job CPU Time	42.0 Seconds
link to .log file

An NH₃ molecule was drawn in Gaussview™ and an optimisation carried out directly with the relatively high basis set 6-31G(d,p) as it is a small, simple molecule. A B3LYP method was once again used and no symmetry was applied by using the "nosymm" phrase. Table summarises the results, including a picture of the optimised molecule along with the important optimised bond lengths and angles.

Table 18

Item Table for NH3 Optimisation Using a 6-31G(d,p) Basis Set

Item Value Threshold Converged? Maximum Force 0.000024 0.000450 YES RMS Force 0.000012 0.000300 YES Maximum Displacement 0.000079 0.001800 YES RMS Displacement 0.000053 0.001200 YES Predicted change in Energy=-1.629728D-09 Optimization completed. -- Stationary point found. ----------------------------  ! Optimized Parameters  !  ! (Angstroms and Degrees)  ! -------------------------- --------------------------  ! Name Definition Value Derivative Info.  ! --------------------------------------------------------------------------------  ! R1 R(1,2) 1.018 -DE/DX = 0.0  !  ! R2 R(1,3) 1.018 -DE/DX = 0.0  !  ! R3 R(1,4) 1.018 -DE/DX = 0.0  !  ! A1 A(2,1,3) 105.7413 -DE/DX = 0.0  !  ! A2 A(2,1,4) 105.7486 -DE/DX = 0.0  !  ! A3 A(3,1,4) 105.7479 -DE/DX = 0.0  !  ! D1 D(2,1,4,3) -111.8631 -DE/DX = 0.0  ! -------------------------------------------------------------------------------- GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

The RMS gradient and derivatives in the tables above are both signs that there is convergence in the optimisation. The optimised bond length is consistent with equilibrium bond length in literature (1.08Å)

Frequency Analysis of NH₃

A frequency analysis was then run on the optimised ammonia molecule above. The same method and basis sets were used along with the phrase "int=grid=ultrafine". Table displays the result summary of the frequency analysis.

The item table below shows the low frequencies of the molecule, the first six of which are within the ±15cm^-1 threshold. No negative frequencies were found, meaning the frequency analysis was a success in finding a minimum.

Table 19: NH₃ Frequency Summary (6-31(d,p))

File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31(d,p)
Charge	0
E(RB3LYP)	-56.55776872 a.u.
RMS Gradient Norm	0.00000823 a.u.
Dipole Moment	1.8464 Debye
Point Group	C1
Job CPU Time	33.0 Seconds
link to .log file

Table 20

Item Table for NH3 Frequency Analysis Using a 6-31G(d,p) Basis Set

Low frequencies --- -10.2450 -0.0017 -0.0009 0.0010 9.1073 14.6705 Low frequencies --- 1089.3141 1693.9157 1693.9487 Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering activities (A**4/AMU), depolarization ratios for plane and unpolarized incident light, reduced masses (AMU), force constants (mDyne/A), and normal coordinates: 1 2 3 A A A Frequencies -- 1089.3141 1693.9157 1693.9487 Red. masses -- 1.1800 1.0644 1.0644 Frc consts -- 0.8250 1.7995 1.7996 IR Inten -- 145.4448 13.5608 13.5561 Atom AN X Y Z X Y Z X Y Z 1 7 0.12 0.00 0.00 0.00 0.05 0.04 0.00 0.04 -0.05 2 1 -0.53 -0.21 0.00 0.21 0.12 -0.45 0.16 0.09 0.61 3 1 -0.53 0.11 0.18 -0.24 -0.19 0.27 0.10 -0.63 0.30 4 1 -0.53 0.11 -0.18 0.03 -0.66 -0.36 -0.26 0.00 -0.17 4 5 6 A A A Frequencies -- 3461.2779 3589.7745 3589.9089 Red. masses -- 1.0272 1.0883 1.0883 Frc consts -- 7.2509 8.2633 8.2639 IR Inten -- 1.0589 0.2691 0.2699 Atom AN X Y Z X Y Z X Y Z 1 7 -0.04 0.00 0.00 0.00 -0.03 0.07 0.00 0.07 0.03 2 1 0.18 -0.55 0.00 -0.12 0.30 0.02 0.28 -0.69 0.01 3 1 0.18 0.27 0.47 -0.18 -0.24 -0.38 -0.25 -0.29 -0.53 4 1 0.18 0.27 -0.48 0.31 0.38 -0.65 -0.03 -0.02 0.08

Population Analysis of NH₃

A population analysis was run on ammonia so that the charge distribution of the molecule could be determined, along with molecular orbitals. The population calculation (6-31G(d,p) basis set, RB3LYP method) was uploaded onto D-space and can be accessed here: DOI:1042/22916

Figure 7: Charge distribution within a molecule of optimised ammonia. The red colour represents negative charge whilst the green represents positive charge.

Figure 8: Specific NBO charges within a molecule of optimised ammonia.

Figure 6: Molecular orbitals of ammonia

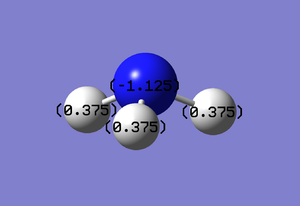
Figure 6 shows the molecular orbitals in order of increasing energy.

The NBO calculations show how charge is distributed within the molecule. In ammonia, the expectation is a formal negative charge based on the nitrogen atom and equal formal positive charges on all three hydrogen atoms. This is due to nitrogen being far more electronegative than hydrogen. Figures 7 and 8 confirm that this is the case in the optimised molecule, with a charge range of -1.0 to +1.0 used in the charge distribution analysis.

Analysis of NH₃BH₃

Optimising a molecule of NH₃BH₃

NH₃BH₃ was optimised using a 6-31G(d,p) basis set and B3LYP method. No symmetry was applied using the "nosymm" phrase. Table 21 presents the summary of the optimisation including key bond lengths and angles, along with an image of the optimised molecule.

Table 21

NH3BH3 Optimisation: 6-31G(d,p) Basis Set
Optimised H-B-H bond angles: 113.88° Optimised H-N-H bond angles: 107.87° Optimised B-H bond lengths: 1.21004Å Optimised N-H bond lengths: 1.01859Å Optimised B-N bond length: 1.66814Å
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
E(RB3LYP)	-83.22469032 a.u.
RMS Gradient	0.00005935 a.u.
Dipole Moment	5.5648 Debye
Point Group	C1
Job CPU Time	1 minute 29.0 seconds
link to .log file

Table 22

Item Table for NH3BH3 Optimisation Using a 6-31G(d,p) Basis Set

Item Value Threshold Converged? Maximum Force 0.000121 0.000450 YES RMS Force 0.000057 0.000300 YES Maximum Displacement 0.000508 0.001800 YES RMS Displacement 0.000294 0.001200 YES Predicted change in Energy=-1.611643D-07 Optimization completed. -- Stationary point found. ----------------------------  ! Optimized Parameters  !  ! (Angstroms and Degrees)  ! -------------------------- --------------------------  ! Name Definition Value Derivative Info.  ! --------------------------------------------------------------------------------  ! R1 R(1,8) 1.0186 -DE/DX = -0.0001  !  ! R2 R(2,8) 1.0186 -DE/DX = -0.0001  !  ! R3 R(3,8) 1.0186 -DE/DX = -0.0001  !  ! R4 R(4,7) 1.21 -DE/DX = -0.0001  !  ! R5 R(5,7) 1.21 -DE/DX = -0.0001  !  ! R6 R(6,7) 1.21 -DE/DX = -0.0001  !  ! R7 R(7,8) 1.6681 -DE/DX = -0.0001  !  ! A1 A(4,7,5) 113.8796 -DE/DX = 0.0  !  ! A2 A(4,7,6) 113.8796 -DE/DX = 0.0  !  ! A3 A(4,7,8) 104.5972 -DE/DX = 0.0  !  ! A4 A(5,7,6) 113.8728 -DE/DX = 0.0  !  ! A5 A(5,7,8) 104.591 -DE/DX = 0.0  !  ! A6 A(6,7,8) 104.591 -DE/DX = 0.0  !  ! A7 A(1,8,2) 107.873 -DE/DX = 0.0  !  ! A8 A(1,8,3) 107.873 -DE/DX = 0.0  !  ! A9 A(1,8,7) 111.0212 -DE/DX = 0.0  !  ! A10 A(2,8,3) 107.8692 -DE/DX = 0.0  !  ! A11 A(2,8,7) 111.0298 -DE/DX = 0.0  !  ! A12 A(3,8,7) 111.0297 -DE/DX = 0.0  !  ! D1 D(4,7,8,1) 179.9998 -DE/DX = 0.0  !  ! D2 D(4,7,8,2) -60.0005 -DE/DX = 0.0  !  ! D3 D(4,7,8,3) 60.0001 -DE/DX = 0.0  !  ! D4 D(5,7,8,1) -59.9967 -DE/DX = 0.0  !  ! D5 D(5,7,8,2) 60.003 -DE/DX = 0.0  !  ! D6 D(5,7,8,3) -179.9964 -DE/DX = 0.0  !  ! D7 D(6,7,8,1) 59.9963 -DE/DX = 0.0  !  ! D8 D(6,7,8,2) 179.996 -DE/DX = 0.0  !  ! D9 D(6,7,8,3) -60.0034 -DE/DX = 0.0  ! -------------------------------------------------------------------------------- GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

The Item table for the optimisation shows there was convergence in the calculation. This is confirmed by looking at the RMS gradient (0.00005935) which is much lower than the threshold 0.001 value.

The optimised H-B-H and H-N-H angles show that the configurations of the ammonia and borane substituents are only mildly affected by the association and that tetrahedral geometries at the N and B centres are not achieved. The optimised B-N bond length of 1.66814Å is in strong agreement with the literature gas-phase B-N length (1.672Å)

Frequency Analysis of NH₃BH₃

A minimum structure was confirmed with frequency analysis. All the six lowest frequencies in the Item table below are within 15cm^-1 and the main frequency modes are all positive (263,633,638, 638, 1069, 1069, 1196, 1204, 1204, 1329, 1676, 1676, 2472, 2532, 2532, 3464, 3581 and 3581cm^-1)

Table 23: NH₃BH₃ Frequency Summary (6-31(d,p))

File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31(d,p)
Charge	0
E(RB3LYP)	-56.55776872 a.u.
RMS Gradient Norm	0.00000823 a.u.
Dipole Moment	1.8464 Debye
Point Group	C1
Job CPU Time	33.0 Seconds
link to .log file

Table 24

Item Table for NH3BH3 Frequency Analysis Using a 6-31G(d,p) Basis Set
Low frequencies --- -3.6746 -3.0944 -0.0010 -0.0007 0.0005 3.4507 Low frequencies --- 263.3378 632.9595 638.4305

Energy Comparison: NH₃BH₃, BH₃ and NH₃

Optimisations have been carried out on NH₃BH₃, BH₃ and NH₃ using the 6-31G(d,p) basis set. This means that each of their energies can be directly compared.

The association energy of NH₃BH₃ is the difference in the calculated energy of NH₃BH₃, and the sum of the molecular components; BH₃ and NH₃.

E(NH₃) = -56.55776856 a.u.

E(BH₃) = -26.61532252 a.u.

E(NH₃BH₃)= -83.22469032 a.u.

ΔE_assoc (NH₃BH₃) = E(NH₃BH₃) - [E(NH₃) + E(BH₃)] = -0.05159924 a.u.

As 1 a.u. = 2625.50 kJmol^-1:

ΔE_assoc (NH₃BH₃) = -135.5 kJmol^-1

Bond association is exothermic and hence thermodynamically favoured. The +135.5 kJmol^-1 needed to break this B-N bond is relatively a low amount of energy, indicating a weak bond, in direct agreenent with the long bond length of 1.66814A calculated from the optimisation relative to N-H and B-H lengths.

The energy of dissociation calculated here is in direct agreement with literature (+140 kJmol^-1)

Mini Project: Ionic Liquids and Designer Solvents

The structures of [N(CH₃)₄]⁺, [P(CH₃)₄]⁺ and [S(CH₃)₃]⁺ were optimised and a frequency, population and NBO calculation was performed on each molecule. The effects of altering the ligands were then investigated by optimisation, frequency and population analysis on [N(CH₃)₃CH₂OH]⁺ and [N(CH₃)₃CH₂CN]⁺. All calculations were performed on the HPC and published to D-Space.

[N(CH₃)₄]⁺

Optimisation

Table 25

[N(CH3)4]+ Optimisation: 6-31G(d,p) Basis Set
Optimised C-N-C bond angles: 109.455° Optimised N-C-H bond angles: 108.878° Optimised H-C-H bond angles: 110.054° Optimised C-N bond length: 1.50936Å Optimised C-H bond lengths: 1.09026Å
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	1
E(RB3LYP)	-214.18127259 a.u.
RMS Gradient	0.00004416 a.u.
Dipole Moment	4.4972 Debye
Point Group	C1
Job CPU Time	4 minutes 52.7 seconds
DOI:10042/22889

An [N(CH₃)₄]⁺ molecule was drawn in Gaussview™ and an optimisation carried out directly with the relatively high basis set 6-31G(d,p). A B3LYP method was used and no symmetry was applied by using the "nosymm" phrase. Table 25 summarises the results, including a picture of the optimised molecule along with the important optimised bond lengths and angles.

Table 26

Item Table for [N(CH3)4]+ Optimisation Using a 6-31G(d,p) Basis Set
Item Value Threshold Converged? Maximum Force 0.000068 0.000450 YES RMS Force 0.000027 0.000300 YES Maximum Displacement 0.000189 0.001800 YES RMS Displacement 0.000079 0.001200 YES Predicted change in Energy=-8.670963D-08 Optimization completed. -- Stationary point found.

The RMS gradient is low and the Item table 26 shows a convergence in the calculation.

Frequency Analysis

The 6-31G(d,p) optimised molecule of [N(CH₃)₄]⁺ underwent frequency analysis. The same basis set and the same method must be applied here for the results to be meaningful, so the frequency analysis was done under a 6-31G(d,p) basis set and R3LYP method. The command "int=grid=ultrafine" was inputted as an additional keyword to reduce the noise by reducing the range of electron density. Table 27 summarises the frequency analysis on the optimised [N(CH₃)₄]⁺ molecule.

Table 28

Item Table for [N(CH3)4]+ Frequency Analysis Using a 6-31G(d,p) Basis Set
Low frequencies --- -5.4773 -2.3150 -0.0003 -0.0002 0.0008 3.9487 Low frequencies --- 183.7597 288.3964 288.9007

The first six low frequencies are low and all the stronger frequencies are positive values, indicative of a minimum [N(CH₃)₄]⁺ structure.

Table 27 - Frequency Analysis [N(CH₃)₄]⁺

File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31(d,p)
Charge	1
E(RB3LYP)	-214.18127322 a.u.
RMS Gradient Norm	0.00000104 a.u.
Dipole Moment	4.4972 Debye
Point Group	C1
Job CPU Time	20 minutes 37.8 Seconds
DOI:10042/22921

Population Analysis

Population analysis was carried out on the optimised molecule of [N(CH₃)₄]⁺ and published to D-space:DOI:10042/22924

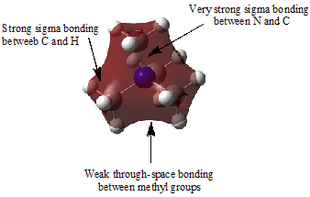
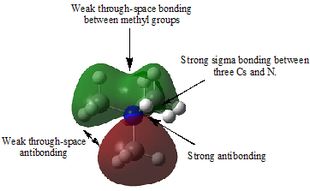
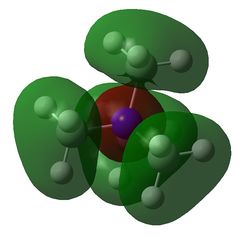
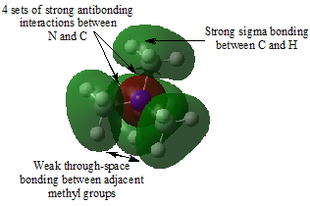
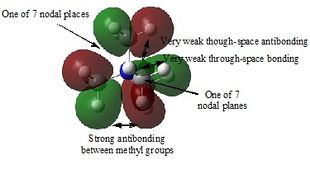
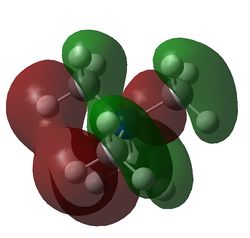
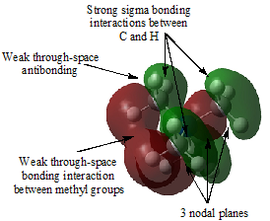
Table 29 shows five different molecular orbitals within the molecule. Some are bonding and others are antibonding. Molecular orbital 21 is the HOMO.

Table 29: Select Molecular Orbitals of [N(CH₃)₄]⁺

MO Number	Energy (a.u)	MO Image	Annotated MO Image	Bonding Description
6				Strongly bonding MO overall. All in-phase interactions and no nodal planes present.
9				Weakly bonding overall due to the presence of one nodal plane.
10				The presebce of 4 nodal planes indicates that this molecular orbital is overall antibonding yet doesn't lie high in energy due to the bonding contributions annotated on the diagram.
18				Molecular orbital 18 is highly antibonding. There are essentially no overall bonding interactions as they are cancelled by weak through space antibonding interactions.
21				There is a lot of bonding and antibonding in this HOMO and so is hard to determine whether this orbital is bonding or antibonding. It could either be non-bonding or slightly antibonding due to three nodal planes.

[P(CH₃)₄]⁺

Optimisation

Table 30

[P(CH3)4]+ Optimisation: 6-31G(d,p) Basis Set
Optimised C-P-C bond angles: 109.525° Optimised P-C-H bond angles: 109.969° Optimised H-C-H bond angles: 109.009° Optimised C-P bond length: 1.81637Å Optimised C-H bond lengths: 1.09333Å
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	1
E(RB3LYP)	-500.82700326 a.u.
RMS Gradient	0.00001657 a.u.
Dipole Moment	2.7342 Debye
Point Group	C1
Job CPU Time	4 minutes 42.2 seconds
DOI:10042/22890

A [P(CH₃)₄]⁺ molecule was drawn in Gaussview™ and an optimisation carried out directly with the relatively high basis set 6-31G(d,p). A B3LYP method was used and no symmetry was applied by using the "nosymm" phrase. Table X summarises the results, including a picture of the optimised molecule along with the important optimised bond lengths and angles.

Table 31

Item Table for [P(CH3)4]+ Optimisation Using a 6-31G(d,p) Basis Set
Item Value Threshold Converged? Maximum Force 0.000032 0.000450 YES RMS Force 0.000012 0.000300 YES Maximum Displacement 0.001162 0.001800 YES RMS Displacement 0.000296 0.001200 YES Predicted change in Energy=-4.016825D-08 Optimization completed. -- Stationary point found.

The RMS gradient is low and the Item table above confirms a convergence.

Frequency Analysis

The 6-31G(d,p) optimised molecule of [P(CH₃)₄]⁺ underwent frequency analysis. The same basis set and the same method must be applied here for the results to be meaningful, so the frequency analysis was done under a 6-31G(d,p) basis set and R3LYP method. The command "int=grid=ultrafine" was inputted as an additional keyword to reduce the noise by reducing the range of electron density. Table Y summarises the frequency analysis on the optimised [P(CH₃)₄]⁺ molecule.

Table 32

Item Table for [P(CH3)4]+ Frequency Analysis Using a 6-31G(d,p) Basis Set
Low frequencies --- -2.5763 -0.0011 0.0008 0.0021 5.2064 7.5840 Low frequencies --- 156.4501 192.0451 192.2812

The first six low frequences are low (between -15 and +15cm^-1) and all the larger vibrational modes are positive. This indicates that the minimum structure for [P(CH₃)₄]⁺ was obtained.

Table 33 - Frequency Analysis [P(CH₃)₄]⁺

File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31(d,p)
Charge	1
E(RB3LYP)	-500.82701172 a.u.
RMS Gradient Norm	0.00000050 a.u.
Dipole Moment	2.7297 Debye
Point Group	C1
Job CPU Time	19 minutes 18.0 Seconds
DOI:10042/22922

Population Analysis

A population analysis was carried out on an optimised structure of [S(CH₃)₃]⁺ and published to D-Space: DOI:22925 .

[S(CH₃)₃]⁺

Optimisation

Table 34

[S(CH3)3]+ Optimisation: 6-31G(d,p) Basis Set
Optimised C-S-C bond angles: 102.771° Optimised S-C-H bond angles: 107.252° Optimised H-C-H bond angles: 111.104° Optimised C-S bond length: 1.82259Å Optimised C-H bond lengths: 1.09137Å
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	1
E(RB3LYP)	-517.68320000 a.u.
RMS Gradient	0.00000972 a.u.
Dipole Moment	5.0148 Debye
Point Group	C1
Job CPU Time	1 minute 38.5 seconds
DOI:10042/22891

An [S(CH₃)₃]⁺ molecule was drawn in Gaussview™ and an optimisation carried out directly with the relatively high basis set 6-31G(d,p). A B3LYP method was used and no symmetry was applied by using the "nosymm" phrase. Table X summarises the results, including a picture of the optimised molecule along with the important optimised bond lengths and angles.

Table 35

Item Table for [S(CH3)3]+ Optimisation Using a 6-31G(d,p) Basis Set
Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.001469 0.001800 YES RMS Displacement 0.000469 0.001200 YES Predicted change in Energy=-1.033595D-08 Optimization completed. -- Stationary point found.

Frequency Analysis

The 6-31G(d,p) optimised molecule of [S(CH₃)₃]⁺ underwent frequency analysis. The same basis set and the same method must be applied here for the results to be meaningful, so the frequency analysis was done under a 6-31G(d,p) basis set and R3LYP method. The command "int=grid=ultrafine" was inputted as an additional keyword to reduce the noise by reducing the range of electron density. Table Y summarises the frequency analysis on the optimised [P(CH₃)₄]⁺ molecule.

Table 37

Item Table for [S(CH3)3]+ Frequency Analysis Using a 6-31G(d,p) Basis Set
Low frequencies --- -3.6594 0.0031 0.0040 0.0040 6.3687 14.5611 Low frequencies --- 162.4884 199.4433 200.7837

The first six low frequences are low (between -15 and +15cm^-1) and all the larger vibrational modes are positive. This indicates that the minimum structure for [S(CH₃)₃]⁺ was obtained.

Table 36 - Frequency Analysis [S(CH₃)₃]⁺

File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31(d,p)
Charge	1
E(RB3LYP)	-517.68327635 a.u.
RMS Gradient Norm	0.00000136 a.u.
Dipole Moment	5.0151 Debye
Point Group	C1
Job CPU Time	9 minutes 16.7 Seconds
DOI:10042/22923

Population Analysis

A population analysis was carried out on an optimised structure of [S(CH₃)₃]⁺ and published to D-Space: DOI:22926 .

Comparison

Structural Comparison

Table 38: Structural Comparison of [N(CH₃)₄]⁺, [P(CH₃)₄]⁺ and [S(CH₃)₃]⁺

Molecule	[N(CH3)4]+	[P(CH3)4]+	[S(CH3)3]+
Gaussview™ Image of Optimised Molecule
C-X bond length (Å)	1.51	1.82	1.82
C-H bond length (Å)	1.09	1.09	1.09
C-X-C bond angle (°)	109.5	109.5	102.8
H-C-H bond angle (°)	110.1	109.0°	111.1°

Table 38 summarises the results obtained from the optimisation calculations for the three molecules.

C-X-C Angles

We shall start by focusing on the central 'X' atom's geometry within each molecule. For both [N(CH₃)₄]⁺ and [P(CH₃)₄]⁺, the C-X-C angle is 109.5°, corresponding to a tetrahedral geometry. The H-C-H bonds in both molecules are also very close to this value so each atom within each of these molecules is part of a tetrahedral geometry. This is not surprising considering that each centre has eight bonding electrons surrounding it and so each bond wishes to be as far apart from the other bonds resulting in tetrahedral geometry. This also shows that steric effects from methyl groups do not intervene with the geometry of the [N(CH₃)₄]⁺ and [P(CH₃)₄]⁺ molecules. The [S(CH₃)₃]⁺ molecule has a C-X-C angle of 102.8°. By inspecting the image of the optimised molecule and considering this C-X-C value, the molecule is said to have a trigonal pyramidal structure, similar to that of ammonia. The sulphur atom has full valence, but only 3 bonding pairs (six electrons). A lone pair is present to achieve this full valence, taking up much more room around the molecule than a bonding pair of electrons. This reduces the angle of the three bonding methyl groups from the desired tetrahedral angle of 109.5° to 102.8°. Each carbon atom is considered to have near-tetrahedral geometry.

C-X Bond Lengths

The bond lengths for C-H bonds within all molecules are 1.09Å. This is not surprising because there is no opportunity for resonance forms or back bonding onto sp³ carbon. Nitrogen is found in group 15 in the second row of the periodic table. Phosphorous is one row down from nitrogen in the same group and sulphur is one group along from phosphorous in group 16. You would therefore expect the nitrogen-based molecule to have the smallest C-X bond length due to the smaller orbitals overlapping with carbon's atomic orbitals much more effectively than the diffuse orbitals of phosphorous and sulphur. This is in agreement with the computational results. In theory, sulphur-based molecule should have the largest C-X bond length due to the orbitals being larger than the phosphorous molecule's. The computational results found the bond lengths to be the same correct to two decimal places. If a more complex basis set was used then a difference between the two C-X lengths to two decimal places may be observed.

NBO Charges

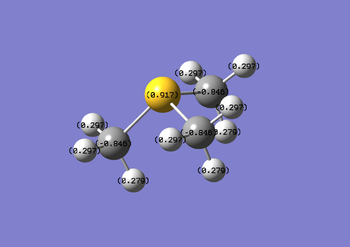
The charge distributions were compared with one another over a colour range of -1.000 to +1.000. Table 39 shows the results of this analysis, along with the NBO charges assigned to each atom within each molecule.

Table 39: NBO Analysis of [N(CH₃)₄]⁺, [P(CH₃)₄]⁺ and [S(CH₃)₃)]⁺

[N(CH3)4]+	[P(CH3)4]+	[S(CH3)3]+

Table 40: Pauling Electronegativity

Atom	Electronegativity (χ)
N	3.04
S	2.58
C	2.55
H	2.20
P	2.19

The differences in charge distribution can be explained by electronegativity. As an atom becomes more electronegative relative to another, the electron density within the bond is shifted towards the more electronegative atom. The greater the extent of electronegativity difference, the greater polarisation of the bond until an extreme is reached where the coloumbic forces between charged atoms dominates the bonding (ionic bonding). Table 40 shows the Pauli negativities for a range of atoms.

Nitrogen is the most electronegative atom compared with carbon, sulphur and phosphorous and so electron density is shifted towards it strongly from carbon resulting in a -0.295 NBO charge. P

Phosphorous is less electronegative than carbon and so the electron density within the P-C bond is shifted towards carbon. A +1.667 NBO charge is therefore assigned to the phosphorous atom.

Sulphur and carbon have similar electronegativities (sulphur being slightly larger) yet there is a significant charge distribution within the molecule. As sulphur is more electronegative than carbon, a slight negative charge placed on the sulphur atom from the three carbons is expected. This is not the case as the sulphur atom has a lone pair which repels electron density away from it, leaving the sulphur atom with a positive NBO charge of +0.917.

Heteroatom Contribution to the C-X Bond

The .log file from the population analysis can help us extract very useful information about the bonds within the cations. The percentage contribution between the two atoms forming a bond can be determined by analysing the "(Occupancy) Bond orbital/ Coefficients/ Hybrids" section of the file. An example is below:

Table 41: % Contribution of X (= N, P or S) to C-X Heteroatom Bond

Cation	X Contribution (%)	C Contribution (%)
[N(CH3)4]+	66.35	33.65
[P(CH3)4]+	40.43	59.57
[S(CH3)3)]+	51.33	48.67

Table 42

C-S Heteroatom Bond Contribution in [S(CH3)3]+

1. (1.98631) BD ( 1) S 1 - C 2 ( 51.33%) 0.7164* S 1 s( 16.95%)p 4.86( 82.42%)d 0.04( 0.63%) 0.0000 0.0001 0.4117 -0.0076 0.0012 0.0000 -0.3441 0.0151 0.0000 0.7354 -0.0324 0.0000 0.4038 0.0259 -0.0380 -0.0263 0.0562 -0.0317 -0.0051 ( 48.67%) 0.6976* C 2 s( 19.71%)p 4.07( 80.16%)d 0.01( 0.14%) 0.0003 0.4437 0.0140 -0.0033 0.3467 -0.0027 -0.7410 0.0058 -0.3635 -0.0098 -0.0204 -0.0102 0.0218 -0.0170 -0.0096

The table represents an S-C bond in [S(CH₃)₃]⁺. 51.33% of the bonding is coming from S whilst 48.67% of the bonding is coming from C. For sulphur, the contribution is roughly 17% s-character and 83% p-character, whereas the carbon contribution is 20% s and 80% p. Using this analysis on all .log files, table B was set up, showing contributions to all C-X heteroatom bonds in the three cations under investigation. There is a direct link between high hetereoatom percentage contribution and low electronegativity, consistent with the NBO charge distribution analysis.

Charge Distribution in [NR₄]⁺

In many pictures, the [NR₄]⁺ cation is depicted with the formal positive charge based on the nitrogen atom, where R is an alkyl group. The "formal" positive charge represents the nitrogen lone pair donating electron density away from the nitrogen atom and onto another. Our NBO analysis on [NR₄]⁺ (R=Me) showed that both nitrogen and the directly bonded carbon atoms both have negative NBO charges associated with them. Inductive effects therefore distribute the formal positive charges onto all hydrogen atoms connected to carbon in the alkyl chain.

Functional Group Effects

Table 43

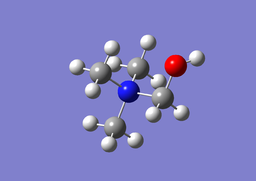
[N(CH3)3(CH2OH)]+ Optimisation
Optimised C-N-C bond angles: 109.594° Optimised H-C-N bond angles: 108.724° Optimised C-O-H bond angle: 111.424° Optimised N-C-O bond angle: 110.550° Optimised C-N1 bond lengths: 1.50377Å Optimised C-N2 bond length: 1.5528Å Optimised C-O bond length: 1.37361Å Optimised O-H bond length: 0.96677Å
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	1
E(RB3LYP)	-289.39470078 a.u.
RMS Gradient	0.00000901 a.u.
Dipole Moment	6.9227 Debye
Point Group	C1
Job CPU Time	38 minutes 13.2 seconds
DOI:10042/22937

The effects of changing a functional group were analysed by adding both electron withdrawing and electron donating groups to the [N(CH₃)₃R]⁺ molecule. Comparison of the charge distributions of the two molecules were carried out and compared to the [N(CH₃)₄]⁺ cation from previous optimisations.

[N(CH₃)₃(CH₂OH)]⁺

Optimisation

The molecule was optimised using a 6-31G(d,p) basis set and B3LYP method. The Item table below shows convergence in the optimisation, further confirmed by the low RMS gradient.

Table 44 [N(CH₃)₃(CH₂OH)]⁺ Frequency Analysis

Item Table for [N(CH3)3(CH2OH)]+ Optimisation Using a 6-31G(d,p) Basis Set
Item Value Threshold Converged? Maximum Force 0.000014 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.001449 0.001800 YES RMS Displacement 0.000452 0.001200 YES Predicted change in Energy=-2.599295D-08 Optimization completed. -- Stationary point found.

Frequency Analysis

Frequency analysis was performed to ensure the optimised structure was a minimum. The low frequencies table below shows that this is the case. All of the higher energetic vibrational modes were positive.

Table 46

Item Table for [N(CH3)3(CH2OH)]+ Frequency Analysis Using a 6-31G(d,p) Basis Set
Low frequencies --- -10.0510 -1.5946 -0.0012 -0.0010 -0.0010 4.8565 Low frequencies --- 130.9961 213.8988 255.5318

Table 45: [N(CH₃)₃(CH₂OH)]⁺ Frequency Analysis

File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31(d,p)
Charge	1
E(RB3LYP)	-289.39470723 a.u.
RMS Gradient Norm	0.0000080 a.u.
Dipole Moment	6.9207 Debye
Point Group	C1
Job CPU Time	26 minutes 15.5 Seconds
DOI:10042/22942

Population Analysis

Population analysis was performed and uploaded onto D-space: DOI:10042/22968

[N(CH₃)₃(CH₂CN)]⁺

Table 43

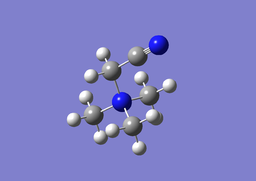
[N(CH3)3(CH2CN)]+ Optimisation
Optimised C-N-C bond angles: 109.594° Optimised H-C-N bond angles: 108.263° Optimised C-C≡N bond angle: 178.844° Optimised N-C-C bond angle: 111.751° Optimised C-N bond length: 1.51427Å Optimised C≡N bond length: 1.15962Å Optimised C-C bond length: 1.45992Å Optimised C-N bond length: 1.52577Å
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	1
E(RB3LYP)	-306.39375724 a.u.
RMS Gradient	0.00008979 a.u.
Dipole Moment	11.7066 Debye
Point Group	C1
Job CPU Time	12 minutes 26.6 seconds
DOI:10042/22941

Optimisation

The molecule was optimised using a 6-31G(d,p) basis set and B3LYP method. The Item table below shows convergence in the optimisation, further confirmed by the low RMS gradient.

Table 44 [N(CH₃)₃(CH₂CN)]⁺ Frequency Analysis

Item Table for [N(CH3)3(CH2OH)]+ Optimisation Using a 6-31G(d,p) Basis Set
Item Value Threshold Converged? Maximum Force 0.000202 0.000450 YES RMS Force 0.000043 0.000300 YES Maximum Displacement 0.001045 0.001800 YES RMS Displacement 0.000284 0.001200 YES Predicted change in Energy=-3.112857D-07 Optimization completed. -- Stationary point found.

Frequency Analysis

Frequency analysis was performed to ensure the optimised structure was a minimum. The low frequencies table below shows that this is the case. All of the higher energetic vibrational modes were positive.

Table 46

Item Table for [N(CH3)3(CH2CN)]+ Frequency Analysis Using a 6-31G(d,p) Basis Set
Low frequencies --- -6.3669 -3.6911 -3.3354 -0.0005 0.0005 0.0013 Low frequencies --- 91.5842 153.8171 211.5424

Table 45: [N(CH₃)₃(CH₂CN)]⁺ Frequency Analysis

File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31(d,p)
Charge	1
E(RB3LYP)	-306.39375724 a.u.
RMS Gradient Norm	0.0000050 a.u.
Dipole Moment	11.7066 Debye
Point Group	C1
Job CPU Time	12 minutes 26.6 Seconds
DOI:10042/22948

Population Analysis

Population analysis was performed and uploaded onto D-space: DOI:10042/22969

df

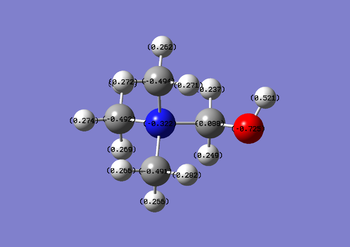
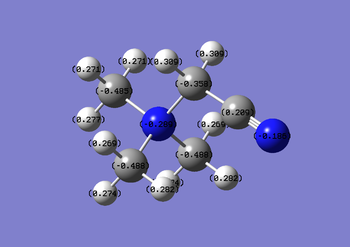
Comparison of [N(CH₃)₄]⁺, [N(CH₃)₃(CH₂OH)]⁺ and [N(CH₃)₃(CH₂CN)]⁺

NBO Charges

Table 39: NBO Charge Distribution Analysis of [N(CH₃)₄]⁺, [N(CH₃)₃(CH₂OH)]⁺ and [N(CH₃)₃(CH₂CN)]⁺

[N(CH3)4]+	[N(CH3)3(CH2OH)]+	[N(CH3)3(CH2CN)]+

Nitrile groups are electron withdrawing, whereas hydroxyl groups are electron donating. It is expected that the inductive effects brought about by these groups will affect the charges of atoms nearby. Increased charge is found on the central N atoms for the OH functionalised cation, the extent of this charge gain is much greater than the extent of the charge loss in the CN functionalised cation (0.027 compared with 0.005). The NBO table spans a colour range of -1.000 to 1.000.

Table 47: HOMOs and LUMOs of [N(CH₃)₄]⁺, [N(CH₃)₃(CH₂OH)]⁺ and [N(CH₃)₃(CH₂CN)]⁺

Cation	HOMO Image	LUMO Image	HOMO Energy (a.u.)	LUMO Energy (a.u.)	Energy Difference between HOMO and LUMO (a.u.)	Energy Difference Between HOMO and LUMO (kJmol-1)
[N(CH3)4]+			-0.57934	-0.13302	0.44632	1171.8
[N(CH3)3(CH2OH)]+			-0.48761	-0.12460	0.36301	953.1
[N(CH3)3(CH2CN)]+			-0.50043	-0.18176	0.31862	836.7

HOMO

From the population analysis results for the three cations it is clear that the OH and CN functional groups both contribute strongly to the HOMO, with little contribution from nitrogen and some methyl groups. For [N(CH₃)₄]⁺, the HOMO is more delocalised over the whole molecule.

Energetically, the HOMOs for both functionalised cations are higher than that of the corresponding methylated cation due to changing atomic orbital energies resulting in a different degree of stabilisation/destabilisation of the molecular orbitals produced.

LUMO

From the population analysis for the three cations, it can be shown that all three LUMOs are delocalised over the whole molecule.

Energetically, the LUMO for [N(CH₃)₃(CH₂OH)]⁺ is higher in energy relative to [N(CH₃)₄]⁺ whereas [N(CH₃)₃(CH₂CN)]⁺ is higher. This is due to different degrees of bonding/antibonding interactions within the changed cations.

HOMO-LUMO Gap

For both functionalised cations, the HOMO-LUMO gap is smaller than that of [N(CH₃)₄]⁺, with [N(CH₃)₃(CH₂CN)]⁺ being the lowest in energy. This would alter the reactivity of the cations. For example, the HOMO controls the energy of an electron loss (oxidation). The larger in energy the LUMO, the less likely reduction will take place. Higher energy HOMOs also correspond to reactive lewis bases, with lower energy LUMOs corresponding to highly reactive lewis acids (e.g. BH₃).