Rep:Mod:daw

Synthesis and Computational Lab: Experiment 1C

Conformational Analysis Using Molecular Dynamics

The Dimerisation and Hydrogenation of Cyclopentadiene

Cyclopentadiene in its simplest form is a useful organic compound, found primarily in metallocenes such as ferrocene and is also used as a precursor to other important organic compounds. Commercially however, cyclopentadiene is available as a dimer as at it dimerises readily at room temperature. When cyclopentadiene dimerises, the dimer produced is governed by the energy of the molecule. By using computational molecular dynamics it is possible to model the energies of the different dimers and justify why one may be prevalent over the others. By studying these energies you can also determine whether the dimer is under kinetic control or thermodynamic control

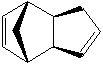
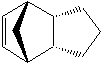
Cyclopentadiene can produce two dimers, endo and exo (1 & 2). By hydrogenating one of the double bonds you can also analyse the energies of the resulting alkenes (3 & 4), and hence deduce which is the most stable kinetically and thermodynamically. As the two double bonds are in different positions, one would expect the energies of the two to consequentially be different. The energies of the different molecules can be modelled computationally using ChemBio3D software which applies an MM2 force field onto the molecules. All energies are given in kcal/mol.

Table 1: Minimised energies for different cyclopentadienes and their hydrogenated products (all energies in kcal/mol)

Molecule Name	Endo Cyclopentadiene Dimer (1)	Exo Cyclopentadiene Dimer (2)	Hydrogenated Alkene (3)	Hydrogenated Alkene (4)
Structure
Stretch	1.2508	1.2851	1.1302	1.2489
Bend	20.8477	20.5805	13.0158	19.1607
Stretch-Bend	-0.8358	-0.8380	-0.5651	-0.8354
Torsion	9.5109	7.6555	12.4117	11.0731
Non 1,4 VDW	-1.5439	-1.4174	-1.0722	-1.6415
1,4 VDW	4.3201	4.2333	4.4400	5.7964
Dipole - Dipole	0.4476	0.3775	0.1410	0.1622
Total Energy	33.9975	31.8764	34.8059	29.2475

The energies of each molecule are broken down into the different effects that are the source of the energy (stretches, torsion etc). Looking first at the dimers, it is clear that the exo dimer (2) has the lowest energy and is therefore the thermodynamic product of the dimerisation. The main difference between the two molecule energies lies in the torsion energy. The endo form has a higher torsional strain due to the two rings being much closer together. Despite this, the endo product is formed more readily than the more thermodynamically stable exo (Commercially available dicyclopentdiene is more than 95% endo).. This means that the dimerisation is under kinetic control. The pi orbitals in the endo transition state align favourably causing the transition state to lower in energy. Therefore the reaction is under kinetic control and hence the endo product is more prevalent. This effect is called the endo addition rule.

Focusing now on the two hydrogenated alkenes, the overall energies of the two molecules are also different. On inspection of the energy breakdown, there are differences in where the source of the energy is. Alkene 3 has more torsional strain but much less bending energy. The cause of these energy differences is the bond angles, which are practically unchanged during hydrogenation due to the rigid nature of the ring structure. In alkene 3 the sp2 hybridised alkene carbons are closer to the favourable bond angle of 120 degrees in VSEPR theory. Therefore it is the thermodynamic product of the hydrogenation.

Atropisomerism in an Intermediate Related to the Synthesis of Taxol

fig. 1: Two atropisomers involved in the synthesis of Taxol

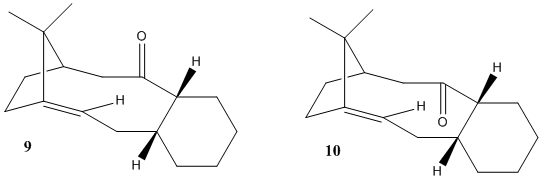
A key drug in the treatment of cancer is Paclitaxel which is used under the commercial name; Taxol. The principle strength of Taxol is its resistance against forms of cancer which do not respond well to conventional chemotherapy. The complete synthesis of Taxol goes via an intermediate which is a mixture of isomers which are dependent on whether the carbonyl group is pointing up or down (see fig. 1). As with cyclopentadiene, when left to stand the racemic mixture favours one isomer and molecules of the other isomerises to produce the more stable compound. This is an example of atropisomerisation. By using computational molecular dynamics on ChemBio3D the energy breakdown of each isomer was obtained to explain this effect.

Like any structure with a six membered ring, the conformation of the ring plays a large part in the behaviour and energy of the molecule. For each of the atropisomers in fig. 1, the cyclohexane ring can be in two different chair conformations as well as two twist-boat confirmations. by minimising the energy in each situation it was possible to compare the conformations. Purely by observing the energy profile of the interconversion between the two chair conformations of cyclohexane it is clear that the most stable conformer will not be the twist boat so only the chair conformers will be considered:

Table 2: Minimized energies of different configurations of an intermediate in Taxol synthesis

	Molecule 9		Molecule 10
	Chair A	Chair B	Chair A	Chair B
Total Energy (kcal/mol)	47.8395	44.2887	42.6828	52.5418

From briefly observing the total energy values it is clear that the most thermodynamically stable atropisomer is a chair conformation of molecule 10 (with the carbonyl pointing away from the bridge). The lowest energy isomers of 9 and 10 were compared by studying the complete energy breakdown to identify where the principal differences lie:

Table 3: Energy breakdowns for lowest energy Taxol transition states (all energues in kcal/mol)

	Molecule 9 (B)	Molecule 10 (A)
Stretch	2.6372	2.6206
Bend	12.5578	11.3394
Stretch-Bend	0.4249	0.3432
Torsion	19.1179	19.6718
Non-1,4 VDW	-1.6077	-2.1619
1,4 VDW	12.8604	12.8721
Dipole-Dipole	-1.7019	-2.0023
Total Energy	44.2887	42.6828

While the energies of the two isomers are similar it is clear that the largest difference lies in the bend energy. The proximity of the isopropyl bridge to the carbonyl in molecule 9 may cause deviation from the ideal sp2 bond angle of 120 degrees. By inspecting these bond angles there was a clear difference. In molecule 10 (A), the angles are 120, 120.3 and 119.7 whereas in molecule 9 (B) they are 120, 121 and 119. Although this difference is slight, it contributes to the deviation of the bonds from their ideal position and hence increases the energy. The overall energy analysis draws the conclusion that the most thermodynamically stable atropisomer is a chair conformer of molecule 10.

The isomerisation during taxol synthesis is not the only phenomenon that affects the reaction. These atropisomers display an interesting property: the alkene double bond reacts very slowly. On small ring systems with a bridge, double bonds adjacent to the bridge undergo considerable strain causing them to react heavily. However on larger ring systems like the one in question, this strain is less so than if the double bond were just a single bond. This "hyperstability" of the alkene is responsible for the lower energy of the bond and hence it is less susceptible to reaction.

Spectroscopic Simulation using Quantum Mechanics

Spectroscopy of an Intermediate Related to the Synthesis of Taxol

fig. 2: Derivatives of the Intermediates in the Synthesis of Taxol

Following on from the energy analysis of the Taxol intermediates, the next step was to use computational techniques to predict the 13C and 1H NMR spectra of derivatives of these intermediates (see fig. 3). When it came to choosing which molecule to analyse, 18 was selected because, as shown in the previous part of the investigation, it is this atropisomer which is the lowest in energy and the most thermodynamically stable. As the last section focused on differentiating between two different atropisomers, it was decided that in this section different conformers would be compared. One chair conformer and one boat were minimised in energy on ChemBio3D. The next stage was to submit the NMR calculation to the HCP supercomputer to compute the NMR prediction. The final output of the calculation was viewed on GaussView 5.0.

In order to determine which conformer was the more accurate, the true experimental NMR values were obtained from the literature before being compared with the artificially predicted results.

fig. 3: Computed 1H NMR of Taxol Chair Conformer

fig. 4: Computed 1H NMR of Taxol Boat Conformer

Table 4: Literature 1H NMR values and computed 1H NMR predictions for different taxol intermediate configurations

Literature NMR Value (ppm)	Boat Conformer NMR Values (ppm)	Chair Conformer NMR Values (ppm)
5.21 (m, 1H)	5.28 (1H)	6.30 (1H)
3.00-2.70 (m, 6H)	3.32 (1H)	3.28 (1H)
2.70-2.35 (m, 4H)	3.22 (1H)	3.21 (1H)
2.20-1.70 (m, 6H)	3.11 - 3.12 (3H)	3.06 (1H)
1.58 (t, 1H)	2.87 (1H)	3.05 (2H)
1.50-1.20 (m, 3H)	2.85 (2H)	3.00 (3H)
1.10 (s, 3H)	2.45 (1H)	2.64 (1H)
1.07 (s, 3H)	2.40 (1H)	2.52-2.53 (3H)
1.03 (s, 3H)	2.30 (1H)	2.51 (3H)
	2.26-2.27 (5H)	2.46 (4H)
	2.09 (1H)	2.40 (1H)
	1.98 (1H)	2.31 (1H)
	1.95 (2H)	2.29 (2H)
	1.84-1.86 (3H)	2.26 (3H)
	1.67-1.68 (3H)	2.24 (4H)
	1.62 (1H)	2.16 (1H)
	1.52 (1H)	2.11 (2H)
	1.47 (2H)	2.00 (1H)
	1.41 (1H)	1.64 (1H)
	1.35 (1H)	1.62 (2H)
	1.16 (1H)	1.53 (1H)
	1.08 (1H)	1.32 (1H)
	1.06 (2H)	1.21-1.22 (3H)
	1.05 (3H)	0.93-0.94 (3H)
	0.96-0.97 (3H)	0.92 (3H)
		0.84 (1H)
		0.55 (1H)

In general it is problematic trying to match the computed nmrs with the literature as the multiplets are very difficult to define. Some peaks in the predicted NMR are purely made up of overlapping multiplets from different signals. However, there are some features that can contribute to deciding which configuration is more appropriate. The first is the singlet at 5.21 in the literature which corresponds to the solitary alkene proton. The value for the boat confirmation is very similar whereas the value for the chair conformer shows a far greater level of deshielding. As well as this, the boat configuration NMR does tend to show signals at similar ppm to the literature, particularly compared to the chair. However, the ambiguity in this particular case does demonstrate why purely computational methods are not always sufficient to predict molecular and reaction behaviour.

fig. 5: Computed 13C NMR of Taxol Chair Conformer

fig. 6: Computed 13C NMR of Taxol Boat Conformer

Table 5: Literature 13C NMR values and computed 13C NMR predictions for different taxol intermediate configurations

Literature NMR Value (ppm)	Boat Conformer NMR Values (ppm)	Chair Conformer NMR Values (ppm)
211.49	211.83	215.37
148.72	148.67	145.29
120.90	118.83	124.20
74.61	89.09	91.01
60.53	67.89	59.72
51.30	56.11	52.95
50.94	55.60	52.80
45.53	50.11	51.16
43.28	48.20	50.28
40.82	44.22	49.85
38.73	42.04	46.54
36.78	37.59	42.03
35.47	35.31	40.59
30.84	31.05	31.01
30.00	28.85	29.63
25.56	28.66	28.84
25.35	25.73	27.05
22.21	25.26	26.59
21.39	23.39	22.01
19.83	21.05	19.77

In contrast to the 1H NMR, the 13C NMR is a lot simpler to analyse and in general the spectra for both the chair and boat are fairly similar with most signals being with 6 ppm of each other. This makes sense as a change in conformation changes hydrogen position by far more than the carbons and therefore the shielding is liable to change by a greater amount. The largest discrepancy comes where the signal ranges between 74 and 91 ppm. This particular carbon is connected to two sulphur atoms which may be the reason why chaging conformation affects the NMR by more than the others. However, the fact neither predicted signal matches the literature imlies that neither conformation is completely accurate.

Gibbs Free Energy

The output from the HPC was also used to find the Gibbs free energy of each molecule. The energy is given in Hartrees/particle which can be converted into kj/mol by using a conversion factor of 2625.49962:

Table 6: Gibbs free enrgies of the chair and boat configurations

Gibbs Free Energy of Boat Conformer (Hartrees/particle)	Gibbs Free Energy of Chair Conformer (Hartrees/particle)
-1651.401387	-1651.423530

It is clear that the chair configuration has a lower Gibbs free energy than that of the boat, providing further evidence that the chair configuration is the most thermodynamically stable.

Analysis of the Properties of the Synthesised Alkene Epoxides

Alkene epoxidation is a process that often requires catalytic action to take place. Two common catalysts used in this reaction are the Shi and Jacobsen catalysts. As with most organic reactions, the configuration of the final product is important as different configurations have different properties. Of course, the correct configuration can be ascertained by carrying out the experiment in the lab, but the properties of potential products can be measured computationally to predict the most stable configuration.

Crystal Structures of Shi and Jacobsen Catalysts

Using the Cambridge Crystal Database and the ConQuest search engine, the crystal structure of the precursor to the Shi catalyst (molecule 21) was analysed to explain its action in the epoxidation. The code for the precursor on the database was NELQEA and by exporting the crystal structure to ChemBio3D, key areas of the molecule were analysed:

Shi_Precursor

Focusing on the anomeric centres, the C-O bond lengths were analysed to give one anomeric O-C-O with bond lengths of 1.38A and 1.44A while the other had lengths of 1.41A and 1.39A. These bond lengths can be explained by the anomeric effect. For the first anomeric centre, the abnormally high bond length of 1.44A is indicative of a weaker bond. Lone pairs on the oxygen in a multi membered ring (5 membered in this case) can donate electron density into axially positioned C-X sigma* orbitals. In this case C-X is the other C-O bond. As electron density is contributed the bond weakens and lengthens hence the value of 1.44A. The anomeric effect is not present at the other anomeric centre as one C-O bond is equatorial to the other. Electron density cannot be donated due to unfavourable overlap and therefore the bond lengths are the same.

The Shi catalyst readily epoxidises trans alkenes but not cis. The reason for this can be investigated by observing the crystal structure. Epoxidation takes place at an oxirane which occupies the same location as the carbonyl in molecule 21. Therefore it is necessary to visualise the approach of an alkene to this part of the molecule. The orientation of the two five membered rings are at 90 degrees to each other so approach by a cis alkene would undergo substantial steric hindrance. The trans alkene however would have a far clearer approach. Hence trans alkenes are more readily epoxidised in the presence of a shi catalyst than cis alkenes.

Shi_Precursor

In the case of the Jacobsen catalyst as seen above, the site of epoxidation is obstructed by the t-butyl groups separated by a significantly small distance of 2.6A. Therefore the approaching alkene needs approach from either above or below. This favours cis alkenes as both R groups can be pointing away from the tBu groups. The cyclohexane ring takes a chair form which alters the symmetry of the crystal structure. For example, the Mn-N bonds are different in length. This could have slight implications in terms of how the epoxidation takes place.

Calculating Epoxide NMR

The final epoxides from the catalytic reactions were then analysed computationally. The epoxides chosen were styrene oxide and trans stilbene oxide. Again ChemBio3D and an mm2 force field were utilised to obtain the lowest energy form of each epoxide and the HCP was used to compute the NMRs of these molecules. Each epoxide has two chiral enantiomers but their NMRs are identical. Therefore 1 enantiomer of each epoxide was analysed:

fig. 7: Computed 13C NMR of Trans-Stilbene Oxide

fig. 8: Computed 1H NMR of Trans-Stilbene Oxide

Table 7: Literature values and computed values for th NMR spectra of trans-stilbene oxide

Literature 1H NMR Value (ppm)	Trans-Stilbene Oxide Computed 1H NMR Values (ppm)	Literature 13C NMR Value (ppm)	Trans-Stilbene Oxide Computed 13C NMR Values (ppm)
7.26-7.45 (m, 10H)	7.45-7.57 (m, 10H)	136.99	134.09
3.86 (s, 2H)	3.54 (s, 2H)	128.44	124.22
		128.19	123.51/123.21
		125.4	123.07/118.26
		62.81	66.43

This is a good demonstration of where the computed NMR prediction matches the literature fairly well. The values for 1H NMR are all within 0.3 ppm of the literature values. Similarly, the 13C computed values are within 5 ppm which is an indicator that the calculation was a success.

fig. 9: Computed 13C NMR of Styrene Oxide

fig. 10: Computed 1H NMR of Styrene Oxide

Table 8: Literature values and computed values for the NMR spectra of styrene oxide

Literature 1H NMR Value (ppm)	Styrene Oxide Computed 1H NMR Values (ppm)	Literature 13C NMR Value (ppm)	Styrene Oxide Computed 13C NMR Values (ppm)
7.32-7.22 (m, 5H)	7.48-7.29 (m, 5H)	137.6	135.13
3.84 (dd, J = 4.0,2.6 Hz, 1H)	3.66 (1H)	128.5	124.13
3.13 (dd, J = 5.5, 4.1 Hz, 1H)	3.11 (1H)	128.1	123.42
2.81 (dd, J = 5.5, 2.6 Hz, 1H)	2.54 (1H)	125.5	122.96/118.27
		52.4	54.06
		51.2	53.48

Again, the literature values match up well with those predicted by the HCP. However, in the case of styrene oxide, the 1H NMR values are not quite as similar to the literature as trans-stilbene oxide. While the NMR can provide plenty of information about the epoxides, the chiral properties remain elusive as there is no difference between the NMR of R and S styrene oxide.

Assigning Configuration to the Epoxides

While the predicted NMRs produced values similar to the literature, it is impossible to determine the configuration of each epoxide from these. However other methods can be used to assign the configuration.

The optical rotation of the epoxides was predicted theoretically by taking the output from the NMR calculation (with optimized geometry) and running a calculation on the HCP which produced the optical rotation. For R,R-trans-stilbene oxide, the optical rotation calculated was 297.90 degrees. This is fairly close to the literature value of 310 degrees using light with a wavelength of 589nm. For R-styrene oxide, the calculated value was -30.36 degrees which is very similar to the value in the literature of -33.3 degrees. The mirror image of these configurations (S,S trans stilbene and S styrene oxide) would have the same magnitude as the original only with the sign changed.

Optical rotation can help differentiate between epoxides. However, In order to determine energy differences, concentration ratios and the overall enantiomeric excess, it is necessary to look at the properties of the reaction transition state. Trans-beta-methyl styrene oxide was selected to be investigated for the shi epoxidation. The computed log output file from the HCP was provided and produced the thermochemical data for the 8 potential configurations (4 R,R and 4 S,S). The lowest free energy of each of these isomers was selected and the change in free energy of transition between R,R and S,S was calculated. Using ΔG=-RTln(K) the equilibrium constant for the transition at room temperature was calculated:

Table 9: Free energies and equilibrium constants for epoxidation of methyl styrene via Shi catalysis

Free energy of R,R configuration (Hartrees/particle)	Free energy of S,S configuration (Hartrees/particle)	Change in Gibb's free energy (R,R - S,S) (kJ/mol)	K
-1343.032443	-1343.024742	-20.218973	3499.37

The equilibrium constant is the ratio of concentrations so by dividing K by K+1 the enantiomeric excess was determined. This calculation resulted in a prediction that the mixture would be 99.97% S,S configuration which is to be expected due to the very large K value and negative ΔG value. Hence it is to be expected that the final product in the epoxidation of trans-β-methyl styrene will be the S,S epoxide.

The same evaluation was made of the Jacobsen transition states. In this case, there are four potential epoxides and again the lowest energy configuration for R,R and S,S were selected.

Table 10: Free energies and equilibrium constant calculation for epoxidation of methyl styrene via Jacobsen catalysis

Free energy of R,R configuration (Hartrees/particle)	Free energy of S,S configuration (Hartrees/particle)	Change in Gibb's free energy (R,R → S,S) (kJ/mol)	K
-3383.254344	-3383.262481	22.266862	1.250418x10-4

Unlike with the Shi catalyst, the positive ΔG and very small K predict a 99.99% excess of the S,S enantiomer under Jacobsen catalysis. This is a good demonstration of where the catalyst does not only lower the reaction activation energy but also has almost complete control over the stereochemistry of the final product.

Investigating the non-covalent interactions in the active-site of the reaction transition state

So far in this investigation, only covalent bond interactions have been considered in the calculation of energies, NMRs and other properties. However, non covalent interactions (NCI) which are defined by the electron density can also be incorporated to produce more realistic solutions. The epoxide transition state chosen to investigate was a configuration of R-Styrene oxide. Firstly the output from the HCP was used to create a new cube file on gaussview. this then made a rotatable image of the transition state which also included the NCI interactions:

fig. 11: R-Styrene Oxide NCI surfaces

The red ring blow the catalyst oxygen is indicative of bond forming in the transition state and therefore is ignored with regards to NCI analysis. More important is the slightly attractive green surface between the styrene and the catalyst. These attractive interactions cover the entire molecule which demonstrates the potential for successful catalysis. The surfaces are green which implies only weak interaction but the slight blue tinge to some areas imply a stronger interaction.

Investigating the Electronic topology (QTAIM) in the active-site of the reaction transition state

The interaction between styrene and the shi catalyst was investigated further using the Quantum Theory of Atoms in Molecules (QTAIM). Avogadro software was utilised to produce the QTAIM image which shows bond critical points (where the electron density is high):

fig. 12: R-Styrene Oxide QTAIM

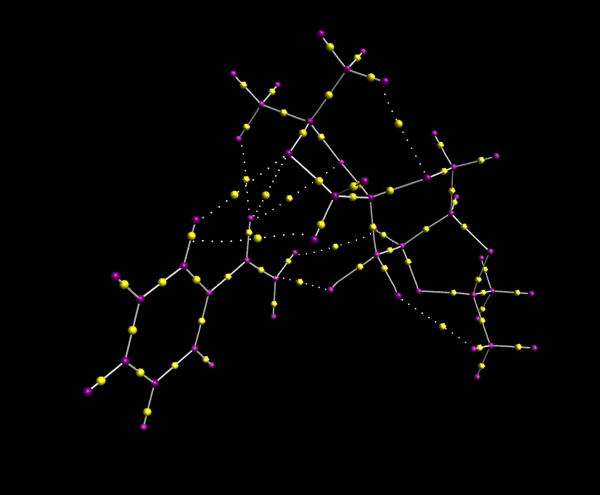
There is no bond critical point (BCP) between the non-terminal, non-aromatic carbon and the catalyst whereas there is one directly between the terminal carbon and the oxygen on the catalyst. This implies that it is this carbon which bonds first in the epoxidation as even though the BCP is weak, it is an indicator of a bond starting to form. QTAIM also describes the nature of the electron density in each bond. In C-C bonds the BCP is central whereas in C-H bonds it lies towards the more electronegative hydrogen and likewise with the electronegative oxygen in C=O bonds. In general there is often weak interaction between oxygen and hydrogen and like the C-C bond the electron density is roughly in the middle of the two atoms when this occurs.

Another Epoxide for Computational Analysis

If this experiment were to be taken further, the same computational analysis could be undertaken on R-(+)-pulegone oxide:

fig. 13: R-(+)-Pulegone Oxide

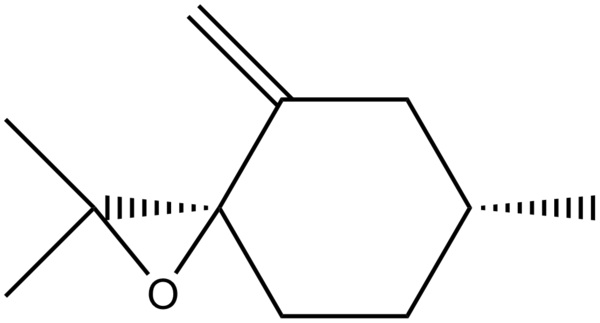
R-(+)-Pulegone, the starting alkene is readily available on Sigma-Aldrich and the literature value of the optical rotation for the epoxide is 853.9 nm in 324 nm light.