Rep:Mod:cwjbear

Modelling transition states

Cameron Jellett

Cope rearrangement: modelling the [3,3]-sigmatropic rearrangement of 1,5-hexadiene

The Cope rearrangement is a [3,3]-sigmatropic shift of 1,5-diene systems, a concerted, suprafacial, pericyclic, heat activated reaction. The case under investigation is a well studied computationally, with several reviews published. The reaction can proceed both in the chair conformation and, the higher energy conformer, boat conformation. It should be noted that

Three transition states are possible: two allyl radicals, an aromatic six-membered ring type system and a 1-4-cyclohexenyl radical as stated by Williams et al. An (earlier) study claim a diradical-type transition state to be the lowest energy for the chair conformation, using the 6-31G* basis set, which is utilised for the tranisition state calculations 1,5-hexadiene for this report. However, the concerted, aromatic transition state will be the mechanism which will be studied.

Optimisation of conformers

Using the Hartree-Fock method and 3-21G basis set, several gauche and anti-periplanar conformers of 1-5-hexadiene were optimised, 6 and 4 of each respectively.

Conformers: Gauche and anti

The different conformers of 1,5-hexadiene were constructed in Gaussview and optimised using the Hartree-Fock/3-21G method/basis set. By drawing the Newman projections and considering the geometry, one would consider the anti-periplanar conformation with the allyl groups facing in opposite directions (shown as anti 2 in the table below) would have the lowest energy configuration. However, this is clearly not the case, indicating the presence of a favorable stereoelectronic interactions between the C=C bonds which are not possible in the anti-periplanar conformations

Conformers (with LOG file)	Image	Central dihedral angle (degrees)	C2C3C4 angle (degrees)	Point group	Ground state energy (a.u)
Anti1 File:ANTI OPT cwj.LOG		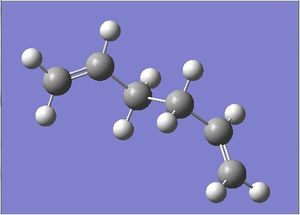180.000	111.367	C2	-231.69260220
Anti 2 File:ANTI2 OPT cwj.LOG		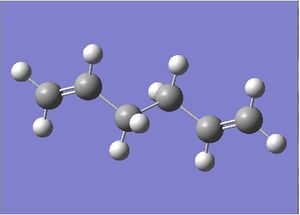180.000	111.343	Ci	-231.69253516
Anti3 DOI:10042/24224		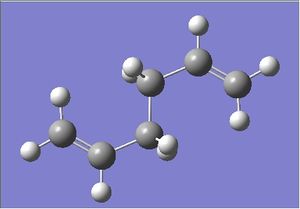180.000	111.367	C2h	-231.68907067
Anti 4 DOI:10042/24225		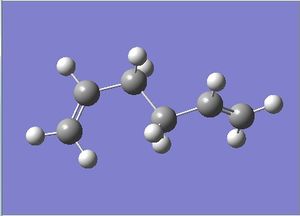180.000	111.343	C1	-231.69097054
Gauche 1 File:GAUCHE OPT cwj.LOG		64.173	112.044	C2	-231.69166702
Gauche 2 File:GAUCHE2 OPT cwj.LOG		63.637	112.382	C2	-231.69153032
Gauche 3 File:GAUCHE3 OPT cwj.LOG		111.772	111.865	C1	-231.69266122
Gauche 4 File:15 GAUCHE4 OPT cwj.log		75.771	116.412	C2	-231.68771617
Gauche 5 DOI:10042/24375		70.228	113.329	C1	-231.68916020
Gauche 6 DOI:10042/24378		71.086	111.973	C1	-231.68961576

The conformation "Gauche 3" has the lowest conformational energy of the possible conformers. However, considering that we are looking at the Cope rearrangement, it is easy to see that this conformer is not important when considering the geometry of the reaction. The anti-conformers have the correct geometry for the reaction. The conformer "anti 2" was re-optimised using a better basis set and different method (DFT/6-31G(d)/B3LYP) for use later on when optimising transition statesFile:15 ANTI2 OPT631G 2.LOG. The dihedral angle remained at 180.000^o but the C₂C₃C₄ angle increased to 112.672^o. The ground state energy also reduced to -234.61170273a.u, but valid direct comparisons of ground state energies can only be made between conformers when the same basis set and method is used.

By visualising some of the MOs from the gauche conformers, the presence of through-space attractive interactions between the C=C double bonds.

Frequency analysis

A frequency analysis was carried out on the DFT/6-31G anti conformer, to ensure that the minima calculated is in fact a minima by ensuring that there are no negative frequencies (this would indicate the presence of a transition state). No negative frequencies were present, indicating that a minima was reached.File:15 ANTI2 FREQ CWJ.LOG

From the output stream file, some thermodynamic parameters can also be found

Thermochemistry

Parameter	value
	at OK	at 298.15K and 1atm
Sum of electronic and zero point energies		-234.469212
Sum of electronic and thermal energies		-234.461856
Sum of thermal and thermal enthalpies		-234.460912
Sum of thermal and electronic free energies		-234.500822

Optimisation of the transition state of the chair and boat conformation

Chair

An allyl fragment (CH₂CHCH₂) was constructed and optimised using the HF/3-21G method and basis set. File:ALLYLFRAGMENT OPT 321G CWJ.LOG

Optimised planar allyl fragment

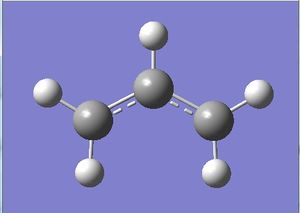
The transition state for the chair conformation (C_2h symmetry) was then constructed approximately using two optimised allyl fragments, with the pair of terminal carbon atoms which form or break bonds at about 2.2A.

The Berney transition state was then optimised and the frequency analysis carried out, for the guessed chair transition state, with the 'opt=noeigen' keyword and the 'once' option in the calculate force constant drop menu selected. Initial attempts failed due to the 'geom=connectivity' keyword which was present at default. The molecule had a ground state energy of -231.61932245a.u and a negative vibration at -817.97cm^-1 showing the motion of the transition state, as expected. File:Chair transitionstate guess 1 cwj.chk

Transition state

.

Another method of optimising the transition state was also used, making use of frozen coodinates File:CHAIR OPT FROZEN BOND.LOGFile:CHAIR TRANSITION FROZEN BOND.LOG. The terminal bonds that were broken/formed in the guessed transition state structure were frozen at ~2.2A and the structure optimised, allowing the remaining atoms to be optimised. The optimised structure then had the bonds changed from 'frozen' to 'derivative' in the redundant bond editor and the Berny transition state optimisation calculation carried out, without the force constants being calculated. The advantage of this technique is that the molecules can be optimised seperately before the calculation of the transition state. This is especially advantageous when the structure of the transition state is unknown.

Both methods give almost identical bond lengths and transition state structures/energies:

Chair conformation

Parameter	Guessed structure (A)	Redundant structure (A)
Terminal carbon lengths	2.02(042)	2.01(985)
C-C bonds	1.38(930)	1.38(933)

Intrinsic reaction coordinate

The IRC calculation for the chair conformation was carried out, initially with 50 steps in the forward direction only, and the force constants only calculated once, showing the positions of the atoms along the potential surface during the reaction. DOI:10042/24159

for initial IRC calculation

The IRC calculation was carried out again with 50 steps, with the force constant recalculated at each step in order to try and obtain a more accurate picture. DOI:10042/24248

for improved IRC calculation

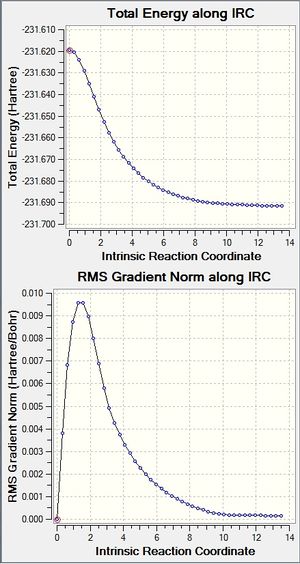
The conformer obtained at the end of the reaction coordinate was "gauche1" from the table of possible conformers.

The Newman projection of the 'final product' for the chair conformation

Boat conformer

The QTS2 method at the HF/3-21G method/basis set was employed for this optimisation, allowing the structure of the reactants and products to be specified explicitly. The transition state given will be interpolated using the lowest energy pathway, which is a limitation of the method as this is an assumption which is not necessarily true.

Initially the C_i anti conformer is used, and the atoms numbered to correspond to the final and initial states. Unfortunately this calculation fails (as expected) due to the final and initial state structures being too far from the actual transition state, which is rectified by changing the dihedral angle by 180^o on both the final and initial states.

The activation energy of reaching the transition state from the initial ground state can then be calculated by finding the difference in energy between the energy of the transition state and the initial state, ensuring that the calculations have the same method and basis set for a valid comparison. The initial state in this case corresponds to "gauche 1", with a ground state energy of -234.61070757 a.u. DOI:10042/24352 . The transition state energy was first optimsed for the HF/3-21G level File:BOAT QST2 OPTANDFREQ 2.LOG, with the structure and vibrations as shown in the animation.

Boat transition state

. However for an accurate estimate of the activation energy, a higher basis set and better method needs to be used, so the structures was reoptimised at the 6-31G*/B3LYP level (ChairDOI:10042/24381 boatDOI:10042/24380 ).

Energies for 6-31G*/B3LYP at 0K

Molecule	Energy (hartrees)	Energy (kcalmol-1)	Experimenal energy (kcalmol-1)
Gauche 1	-234.61070757
Boat transition state	-234.54309271
Chair transition state	-234.55693088
Boat activation energy	0.06761486	42.43	44.7 ± 2.0
Chair activation energy	0.05377669	33.75	33.5 ± 0.5

In both cases, the activation energies are within experimental values at the B3LYP/6-31G* level

Summary of the Cope rearrangement and the methods used

The chair transition state was found to be of a lower activation energy when considering the six membered ring aromatic transition state. Several ways of calculating the energies were used, with correlation on the chair transition state using two methods.

When computing energies, it is important to consider the scope and limitations of the method/basis set employed. The Hartree-Fock method, used for this study, has some important sources of error which need to be noted. This is an ab-initio method used to solve the Schrodinger equation, assuming that the total electronic wavefunction describing the molecule can be split in to a product of the separate wavefunctions(a reasonable approximation), allowing the wavefunction to be solved exactly for a one electron problem and allowing much faster iterative methods to be used in the case of a many-electron problem. However, the biggest source of error for the HF method is due to the lack of consideration of the electron coloumb correlation energy, which is the repulsion of electrons in space due to their charge.

As a result of this, the energy calculated is always higher than the experimental values.

The [2+2]-cycloaddition of ethylene to butadiene

Due to the requirement of a cis conformation for butadiene (approximately 96% at room temperature) and large HOMO-LUMO gap between two unsubstituted alkenes this reaction does not proceed appreciably. However, it can be modelled using computational techniques.

Using the qualitative MO diagrams of ethylene and butadiene, the orbital overlap between the π* of the ethene and the HOMO of the butadiene and the п orbital of the ethene and the LUMO of the butadiene can be seen to be of the correct symmetry for a constructive overlap, as shown in the diagram

The qualitative MO diagram with corresponding calculated MOs

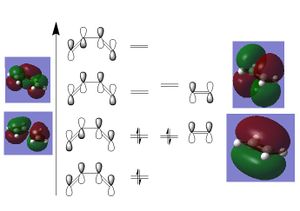
. This frontier orbital analysis of the reaction shows that the reaction is allowed according to symmetry Cis-butadiene was constructed in gaussview and optimised using a semi-emperical method and AM1 basis set. The final structure had a dihedral bond angle of -14.000^o DOI:10042/24235 . The MOs of butadiene were constructed and are in agreement with the predicted symmetry and shape from the qualitative MO diagram.DOI:10042/24379

the HOMO(anti-symmetric) (left) and LUMO (symmetric)(right)

A guessed structure for the transition state was constructed using previous knowledge gained from the MO analysis/cope rearrangement study, with the ethene approaching the cis-butadiene from the top, with the Berny transition state optimisation calculation being carried out (along with the frequency analysis)File:Opt freq tranisition state cwj.log. The transition state obtained was as expected, with a clear vibration showing this along with a negative frequency at 818.37cm^-1. The calculated HOMO/LUMO surfaces suggest that the LUMO of the transition state is the LUMO of the butadiene and the HOMO of the ethene (symmetric) combining and the HOMO is the LUMO of the ethene and the HOMO of the butadiene combining (antisymmetric). These interactions are allowed according the symmetry, showing a good agreement between the predicted and calculated outcome.

This was then reoptimised at a higher basis set and using a more accurate method, more specifically the DFT/B3LYP 6-31G* method/basis setDOI:10042/24366 . This method takes into account the coloumbic correlation energy, and more fundamentally deals with the electron density as opposed to the electronic wavefunctions as in the HF method.

A typical C-C sp³ bond length is 1.530A and a typical C-C sp² bond length is 1.460A . The Van der Waal radius of carbon is 1.70A The length between the bond-forming carbons in the transition state is 2.20956A, longer than the mentioned carbon-carbon bonds and Van der Waal radius, which is not surprising considering that this is the transition state and the bond is not fully formed yet. The negative frequency indicating the transition state is -818.37cm^-1 and the first real vibration is at 166.54cm^-1, corresponding to the two reacants twisting in opposite directions perpendicular to the bonds being formed.

alt text=

The Diels-Alder reaction between maelic anhydride and 1,3-cyclohexadiene: endo vs exo

The reactant structures were drawn in chemdraw and the opt+freq calculations were carried out to find a minima, using the DFT/6-31G* method basis set.(1,3-cyclohexadiene DOI:10042/24218 , maelic anhydrideDOI:10042/24217 ). The endo transition state was guessed and the transition state optimised to the 6-31G*/B3YLP level DOI:10042/24356 . However, the exo transition state was problematic and initial attempts to optimise directly to the 6-31G*/B3YLP level failed, meaning it was optimised to the AM1/3-21G level first DOI:10042/24357 and then reoptimised to the higher basis setDOI:10042/24358 , working on the first attempt.

The endo transition state structure/vibration

The exo transition state structure/vibration

It is clear from experiments that the endo product is favoured, and in the case being studied it is 85% of the product It is important to note that solvent effects are ignored for these calculations, and experimentally it has been found that solvents can greatly affect the rate/product ratio.

The endo transition state HOMO has 4 nodal planes, three of which are shown and the other which is not. Clearly with a nodal plane in between the two reacants, the secondary-orbital overlap effect, which claims that the endo product is favoured due to an energy lowering interaction between the C=O pi* bonds interacting with the HOMO of the diene.

The endo transition state with calculated MO surfacesDOI:10042/24377

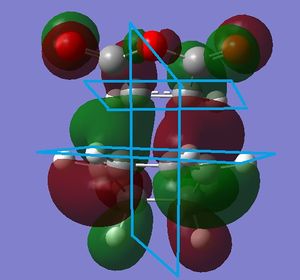
This is also the case for the exo transition state, with the same number of nodal planes and a lack of through space interactions (although this is not predicted for the exo transition state using the secondary orbital overlap idea).

The exo transition state with calculated MO surfacesDOI:10042/24376

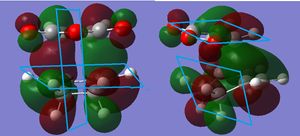
. Indeed the effect has even been considered to be non-existent with solvent and steric effects and hydrogen bonding considered to be the deciding factors

Energies

Molecule/system	Energy (Hartrees)	Energy (kcalmol-1)
Cyclohexa-1,3-diene	-233.41891187
Maelic anhydride	-379.28953546
Exo transition state	-612.67931095
Endo transition state	-612.68339646
Exo transition state activation energy	0.02913638	18.28
Endo transition state activation energy	0.02505087	15.72
endo-exo energy difference	-0.00408551	2.56

However, the literature reported value of 1.2kcalmol^-1, obtained experimentally is less than the value calculated, however, this reaction was carried out in benzene at 80^oC, making the two values difficult to validly compare.