Rep:Mod:cw

Synthesis and Computational Lab: 1C

This page is concerned with the investigation of organic molecules and reactions by molecular modelling. The energies of molecules are used to rationalise proposed reaction pathways and predictions are made for the spectra of compounds.

Conformational Analysis using Molecular Mechanics

The object of molecular mechanics is to predict the energies associated with given molecules, as defined by certain intrinsic constants such as bond force constants and barriers to rotation around specific bonds, together these are known as the force field. There is a fundamental assumption associated with the calculations -that the nuclear and electronic motions are separated (Born-Oppenheimer approximation), which means the computation need only take into account the nuclei of the molecule, drastically simplfying calculations, and allowing the force field to comprise only five contributions. These are the energies associated with

• Bond stretching
• Angle bending
• Torsion
• Non-bonded interactions (van der Waals forces and electrostatic interactions)
• Hydrogen bonding

The hydrogen bonding term has been omitted from these calculations for simplicity. The MMFF94(s) force field is used for these calculations, to optimise the geometry of molecules and produce all the energy values given below. Each energy shows how far from the optimum arrangement the structure is in relation to that parameter, in essence the larger the reported energy (eg bond stretching energy of 3.543 kcalmol⁻¹) the more deviation from the equilibrium bond length, angle, torsion angle, or the presence unfavourable van der Waals or electrostatic interactions. Occasionally the outcome is a negative value, indicating a more stable conformation.

Dimerisation of Cyclopentadiene

Cyclopentadiene is a synthetically useful small organic molecule; often used as a precursor to the cyclopentadienyl ligand it must be 'cracked' before use to break it down from the readily-formed dimer into monomeric molecules. The dimer, dicylopentadiene, exhibits endo/exo isomerism between isomers 1 and 2 based on stereoelectronic stabilisation of the transition state during the reaction, as seen here. Formation is through a Diels-Alder type pericyclic reaction, with the endo isomer being the major product formed. By studying the relative energies of the two isomers we can rationalise how the reaction proceeds - under either thermodynamic or kinetic control. The total static energy is given in Table 1, along with the Total bond stretching energy, Total angle bending energy, Total torsional energy, Total van der Waals energy and Total electrostatic energy, which allow us to understand the reasons behind the energy differences. All units are in kcalmol⁻¹ .

Table 1. Static energies of cyclopentadiene dimers

	exo-dicyclopentadiene (1)	endo-dicyclopentadiene (2)
	File:Cyclopentadiene 1 again.jpg	File:Cyclopentadiene 2.jpg
Bond stretching energy	3.543	3.467
Angle bending energy	30.781	33.191
Torsional energy	-2.723	-2.949
van der Waals energy	12.790	12.357
Electrostatic energy	13.012	14.184
Total energy	55.373	58.191

The exo-isomer is counter-intuitively the lower in energy and more stable, as it is the less predominant form of dicylopentadiene. The only way this can be justified is by concluding that the reaction is under kinetic control, and the endo-isomer formed faster; in this case the ratio of isomeric products formed is dependent on the relative energies of the transition states not of the products. Hence, under these circumstances, it is feasible for the predominant product to be the higher energy isomer. Looking at the individual contributions to the energies both isomers have very similar deviations from the preferred structure of that component, i.e. longer bonds than the equilibrium bond length for the involved atoms, or torsional strain around a twisted bond. The geometrical energies relating to bond stretching, torsion angle and van der Waals forces are all within 0.5 kcalmol⁻¹ , while the clearest distinction is between the angle bending. The endo form has angles bent further away from the natural bond angles, which raises the energy.

Hydrogenation of Dicyclopentadiene

The hydrogenation of the more prevalent endo-dicyclopentadiene is also explored through energy optimisations of the potential products; either of the two double bounds could be hydrogenated. Eventually the molecule would be hydrogenated completely, but the formation of the dihydro-intermediate is the limit of this investigation. The results are summarised in Table 2, all values in kcalmol⁻¹.

Table 2. Static energies of hydrogenated dicyclopentadiene

	dihydro-dicyclopentadiene (3)	dihydro-dicyclopentadiene (4)
	File:Cyclopentadiene 3 hydrogenated.jpg	File:Cyclopentadiene 4 hydrogenated.jpg
Bond stretching energy	3.312	2.823
Angle bending energy	31.935	24.685
Torsional energy	-1.469	-0.379
van der Waals energy	13.637	10.638
Electrostatic energy	5.120	5.147
Total energy	50.446	41.257

Isomer 4 can clearly be seen to be the lower energy hydrogenation product, and therefore the thermodynamic product of the reaction of dicyclopentadiene with hydrogen; in every division the component is nearer its natural value. The greatest contribution to the stability of this isomer is a 7 kcalmol⁻¹ lower energy relating to angle bending, indicating that in this isomer the angles are much nearer to the preferred 109° around a tetrahedral centre. Also, that either the double bond to the right of the diagram is less geometrically strained in comparison to the single bond in isomer 3, or that the new single bond to the left of the diagram is less so in comparison to a double bond at that position. The single bond to the left of the molecule would be expected to supply the greater stabilisation because this end of the molecule contains the bridging cyclopentadiene, thus a double bond here would have expanded and/or compressed angles in order to accommodate the bridge.

Atropisomerism in a synthetic intermediate of Taxol

9 and 10

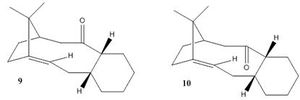
Atropisomerism is an additional form of isomerism; in comparison to endo/exo isomerism, as studied above, the two atropisomers can be isolated, although if left isomerism occurs so that only the more stable isomer remains. Originally reported as 'optical activity due to chirality' , atropisomerism arises when rotation around a bond is restricted, either by bulky substituents or by constraints such as being held in place by a ring. The two isomers 9 and 10 show how the intermediate is primarily synthesised, with the carbonyl group pointing above the general plane of the molecule (as in 9) or beneath (10).

An exploration of which is the more stable isomer is conducted below.

The cyclohexane part of the molecule is key in determining the thermodynamic stability of the isomer as it has strictly defined conformations, with a large range of associated energies. The well known arrangements of cyclohexane can be seen here, where twist-boats and chairs are the only local energy minima, hence calculations to find the lowest energy isomer of the taxol intermediate focused on these conformations.

Figure 3. Conformations of Atropisomer 3

9.1	9.2	9.3
Taxol intermediate 9.1	Taxol intermediate 9.1	Taxol intermediate 9.1

Isomer 9.1 shows the conformation where the carbonyl group points up, with the cyclohexane ring in a stable chair conformation and the rest of the molecule also having staggered as opposed to eclipsed atoms, and favourable gauche interactions. 9.2 is the second conformation to have a cyclohexane chair, this time pointing down from the plane of the molecule generating much higher angle bending and torsional energies as the adjacent ring puckers. The twist-boat isomer, 9.3 is included for comparison; as a twist-boat conformation of cylcohexane it would be expected to be higher in energy.

Table 3. Static energies of intermediate 9

	9.1	9.2	9.3
Bond stretching energy	7.630	8.616	7.930
Angle bending energy	28.266	33.608	29.525
Torsional energy	0.321	3.158	2.765
van der Waals energy	33.144	35.709	34.719
Electrostatic energy	0.303	0.208	0.319
Total energy	70.546	82.929	76.283

The static energies of the respective molecules are included in Table 3. All units are in kcalmol⁻¹. These energies verify that the most stable conformation of the taxol intermediate involves the cyclohexane ring in its stable chair conformation, surprisingly the next most stable involves a twist-boat, inherently less stable, but with reduced angle bending in comparison to 9.2 which suffers from large torsional and angle strain due to the bending of the ring downwards in order to accommodate a chair in that part of the molecule. This also reveals interactions between the rest of the molecule to be non-negligible, particularly with regard to planarity around the double bond.

Atropisomer 10, with the carbonyl pointing 'down' can also be analysed in terms of the cyclohexane ring, and again the results follow the same pattern; a very low energy chair configuration, a chair cyclohexane but suffering from other destablising interactions in the rest of the molecule, and an intermediate-energy twist-boat cyclohexane conformation. Shown in Figure 4.

Figure 4. Conformations of Atropisomer 10

10.1	10.2	10.3
Taxol intermediate 9.1	Taxol intermediate 9.1	Taxol intermediate 9.1

Table 4. Static energies of intermediate 10

	10.1	10.2	10.3
Bond stretching energy	7.598	8.623	7.790
Angle bending energy	18.819	21.768	19.071
Torsional energy	0.247	6.680	3.708
van der Waals energy	33.237	36.047	34.980
Electrostatic energy	-0.053	0.401	-0.063
Total energy	60.553	74.874	66.302

The energies of each conformation is broken down in Table 4. All units are in kcalmol⁻¹ . Between these conformations the evaluation is similar; a chair conformation of the cyclohexane ring to the right hand side gives the greatest stabilisation, although it must be in a position so as not to distort the rest of the molecule, as in 9.2 and 10.2. Interestingly 10.1 and 10.2 have the same total configuration aside from a swapping of the carbons at the front and back of the ring between 'down' and 'up' in the chair configuration in 10.1, and the reverse in 10.2, which brings the ring carbon and its hydrogen atoms into close proximity of the carbonyl oxygen, creating a steric clash. This accounts for the 3 kcalmol⁻¹ difference in the van der Waals energy between the two, as the methylene encroaches on the van der Waals space of the carbonyl.

From this analysis it is easy to ascertain that the two atropisomers exist as 9.1 and 10.1, and that the most stable is atropisomer 10.1. All of the 10 configurations have much lower angle bending energies, while the rest of the energy components are similar.

File:Taxol 10 regioisomer.jpg

Taxol 10.4

These two isomers are exceptionally stable, both exhibiting 'hyperstability' of the bridgehead olefin with the existence of the alkene making the molecule more stable than the corresponding parent alkane. It is possible that all bridgehead alkenes with the double bond in a trans conformation as part of a ring containing ten or more carbon atoms are 'hyperstable', as claimed by Lalitha, Chandrasekhar, and Mehta. The reasons for this are still a topic of debate but could be a result of the 'cage structure' of the alkene. A comparison between 10.1 and the regioisomer 10.4 confirms the hyperstability of the bridgehead alkene; moving the double bond away from a bridgehead position would be expected to create a lower energy molecule, in accordance with Bredt's rule, and yet 10.4 has a total static energy of 74.001 kcalmol⁻¹, almost 14 kcalmol⁻¹ more energetic than 10.1. The stability increase on going from the parent alkane to bridgehead alkene could not be quantified due to constraints on the force field method which do not allow non-isomeric molecules to be compared, although a study has been conducted under different circumstances by J-S Kim. His work rationalises the phenomenon with a change of hybridisation where the alkene meets the bridge reducing large-angle strain and steric clashes. This stabilisation means the intermediate is resistant to hydrogenation, reacting very slowly due to a lack of thermodynamic driving force.

Spectroscopic Simulation using Quantum Dynamics

File:17 and 18.jpg

17 and 18

Table 5. Static energies of intermediates 17 and 18

	17	18
Bond stretching energy	16.434	15.015
Angle bending energy	39.789	30.929
Torsional energy	15.300	9.677
van der Waals energy	51.799	49.390
Electrostatic energy	-7.568	-6.052
Total energy	117.960	100.500

Another way in which computational chemistry has changed the way in which reactions are assessed is through the use of similar software, predicting the spectroscopic data associated with molecules. Comparison with experiential data will verify either a proposed structure of the intended product, or the reaction pathway, should different pathways lead to products differentiatable by spectroscopy. Here, a further two intermediates in the synthesis of Taxol (17 and 18) are compared to find which of the isomers is lower in energy (Isomer 18 is envisioned as the more thermodynamically stable to due its visible similarity to intermediate 10) and the ¹H NMR and ¹³C NMR are predicted. Using the previous methodology the most stable conformation of each isomer has been found, with a chair conformation of the cyclohexane ring on the right, optimised staggering of atoms in the larger ring, maximal planarity of the alkene, and in the case of these isomers near planarity of the dithiane ring which occupies the least sterically crowded area of the molecule. The breakdown of static energies is given in Table 5, all values in kcalmol⁻¹. 18 is shown to much more stable, with the main contributions from a lower angle bending energy, and torsional strain.

Table 6. Gibbs free energies of isomers 17 and 18

Taxol intermediate 17	Taxol intermediate 18
-1036295.14	-1036307.66

Gibbs Free Energy

Further computational simulation of isomers 17 and 18 gives a vibrational analysis of the molecules, by which thermodynamic properties can be calculated. The Gibbs free energy of each isomer is reported in Table 6, in kcalmol⁻¹, supporting the previous conclusion that isomer 18 is lower in energy.

The analysis shows the more stable isomer to be intermdiate 18, thus this molecule was submitted for NMR prediction. The calculated spectra for the chair configuration and twist boat configuration can be viewed via these links, in order that a comparison might be made between the two isomers, the data is summarised in Table 7. Problems arise when simulating spectra of static molecules because molecules are never still but always rotating, bringing some of the protons into the same environment which averages out some of the signals. The most common and obvious examples are the methyl protons, all of which have been assumed to be in equivalent environments, and their three individual signals averaged into one peak, each representing three protons.

Table 7. ¹H NMR comparison for chair and twist-boat conformers of Taxol intermediate 18

Lit. Chemical Shift, multiplicity and integration	Chair Conformation Chemical Shift (ppm), integration	Twist-boat conformation Chemical Shift (ppm), integration
5.21 (m, 1H)	5.97 (1H)	5.48 (1H)
3.00-2.70 (m, 6H)	3.19 (2H)	3.24 (1H)
2.70-2.35 (m, 4H)	3.06 (1H)	3.15 (1H)
2.20-1.70 (m, 6H)	2.96 (1H)	2.97 (2H)
1.58 (t, 1H)	2.77 (3H)	2.82 (1H)
1.50-1.20 (m, 3H)	2.65 (1H)	2.63 (2H)
1.10 (s, 3H)	2.47 (3H)	2.42 (1H)
1.07 (s, 3H)	2.23 (1H)	2.34 (2H)
1.03 (s, 3H)	2.00 (3H)	2.15 (1H)
	1.83 (1H)	2.02 (2H)
	1.58 (1H)	1.89 (1H)
	1.41 (3H)	1.75 (3H)
	1.27 (3H)	1.56 (1H)
	1.25 (3H)	1.44 (3H)
	1.16 (3H)	1.31 (1H)
		1.26 (3H)
		1.16 (3H)

Despite the averaging of the most clear-cut signals that correspond to environments which would be the same in an unfixed molecule, the computational assignment has still produced many more peaks than those reported in literature, making comparison difficult. Easily identifiable is the single alkene proton, recording a signal at 5.21 ppm in a measured sample, both conformers match this closely, in particular the twist-boat conformation of molecule 18. Another good proton to analyse the similarity is chemical shift 1.58 ppm, which is reproduced exactly in the spectrum of the chair-conformation, and very slightly more shielded in the twist-boat (less than 1 ppm). The remaining signals all approximately follow those seen in the literature, although the differences in integration due to overlapping signals being unresolvable experimentally and producing multiplets, creates great difficulty in comparing the shifts of particular proton environments. This highlights the difficulty in using computational NMR methods alone to identify molecules, and to rationalise their properties. The range in chemical shifts produced by calculation corresponds well with the experimental report; both conformers recording slightly higher chemical shifts (differences all <0.5 ppm) as a result of the computational experiment taking place in a hypothetical chloroform solvent while the experimental literature values were recorded in deuterated benzene, having different levels of magnetic activity the solvent difference has caused a slight skew in the calculated peaks. Overall the spectrum of the chair conformation more closely resembles the experimental one, indicating that there is a higher proportion of chair, as-opposed to twist-boat conformers, at any one time in a real sample of Taxol intermediate 18 - as expected due to the greater thermodynamic stability of chair conformations.

The calculated carbon spectra for the chair configuration and twist boat configuration can be viewed via here, the chemical shifts of each atom recorded in Table 8.

Table 8. ¹³C NMR comparison for chair and twist-boat conformers of Taxol intermediate 18

Lit. Chemical Shift	Chair Conformation Chemical Shift (ppm)	Twist-boat conformation Chemical Shift (ppm)
211.49	212.23	209.94
148.72	148.07	149.23
120.90	120.14	118.51
74.61	94.11	91.40
60.53	60.42	64.50
51.30	54.89	55.30
50.94	54.20	54.74
45.53	49.69	50.12
43.28	49.14	45.90
40.82	46.77	41.90
38.73	41.79, integration 2	37.90
36.78	38.74	37.77
35.47	34.13	35.53
30.84	33.64	34.31
30.00	28.15	32.26
25.56	26.46	28.58
25.35	24.54	26.15
22.21	22.62	25.16
21.39	21.71	22.87
19.83		22.46

The outcome of ¹³C NMR calculations is much easier to compare to literature values; the chair and boat conformers have produced exceptionally similar spectra, both with all signals matching the literature values to within 5 ppm. The only exceptions to this are the peak at 74.61 ppm recorded experimentally, which was determined to have much greater shielding at over 90 ppm. Again this reveals a limitation to computational prediction; the atom responsible for these signals is the quaternary carbon linking the six-, and five-membered rings to the right hand side of the molecule. Bonded to both sulphur atoms, the heaviness of these generating spin-orbit coupling, the chemical shift for this carbon becomes very inaccurate. One anomalous result is a peak of integration 2 (41.79 ppm) despite the fact every carbon atom in the chair-conformation (in fact both molecules) is in a different environment but this is simply due to the degeneracy tolerance of the predicted spectrum. Yet another drawback to computational methods, signals within the degeneracy tolerance of 0.5 ppm are automatically condensed together when the two environments are in reality substantially different; one deshielded by adjacency to a sulphur atom , the other, deshielded through space by proximity to the carbonyl oxygen.

Analysis of properties of asymmetrically synthesised alkene epoxides

Catalytic Systems

Shi and Jacobsen catalysts are two important catalysts in asymmetric epoxidation; each catalyses different alkene substrates based on cis/trans conformations, this is a result of the 3D structure of the catalysts themselves, which are analysed below. The 3D Jmol image of Shi catalyst can be found .

File:Shi 21 with atom numbering.jpg

Shi catalyst 21

The bond lengths labelled on the 3D image can be rationalised using the anomeric effect. This occurrence gives an unexpected stability to α-anomers (anomeric oxygen axial) as a result of the donation of a ring oxygen lone pair into the σ* orbital of an antiperiplanar C-O bond. Most commonly seen in six-membered rings, donation of the O(12) lone pair into σ*C(14)-O(8) would be expected to shorten O(12)-C(14) from the standard bond length of 1.43 Å, as well as lengthening and weakening C(14)-O(8) due the increased electron density in the antibonding orbital. This is not seen due to the overriding anomeric effect within the 5-membered ring, which orientates oxygen substituents at an anomeric centre in an axial environment more effectively than in 6-membered rings, with a strongly favourable angle for lone pair-σ* overlap. Firstly, donation from O(7) lone pair into σ*C(19)-O(8) justifies the very long 1.44 Å bond length and shortened 1.38 Å C(19)-O(7), while a second anomeric interaction directly counters the interaction based on the 6-membered ring. Donation from O(8) lone pair into σ*C(14)-O(12) explains the surprisingly short axial O(8)-C(14) 1.39 Å bond length. The orientations of the two 5-membered rings protruding from the Shi catalyst brings to light an explanation as to why it catalyses the epoxidation of trans alkenes, and not cis. Their orientation around the catalytic centre (carbonyl oxygen, replaced by dioxirane functionality in the active species), as seen in the 3D image, means that approach of a cis-alkene would be blocked, and that the face a trans alkenes persents to the catalytic centre, results in chirality .

Jacobsen Catalyst

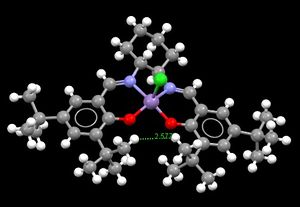
Jacobsen conversely epoxidises cis-alkenes in preference to trans, again as a consequence of parts of the molecule restricting available pathways to the catalytic centre. The Jmol image can be viewed , the static image on the right showing the 2.577 Å gap created by the tert-butyl group substituents on the aromatic ligands, much to small for any alkene to approach from this angle, hence approach can only be from above or below the plane of the molecule. As a cis-alkene can align itself so that the smaller substituents of each end are those pointing towards the Jacobsen molecule, steric hindrance to the reaction can be reduced, while trans-alkenes cannot adopt such a conformation.

Epoxide NMR predictions

The outcome of reactions of two alkenes were also predicted using computationally generated NMR spectra. The epoxidation of trans-alkene, trans-β-methyl styrene, would be catalysed by Shi catalyst due to the differing shapes and constrained geometries of the two catalysts, as explained above. While 1,2-dihydronaphthalene, with the alkene locked in a cis conformation would be catalysed by Jacobsen catalyst. Each epoxide has two enantiomeric forms due to the two chiral centres present in each molecule, however the NMR spectra would appear indistinuishable so only one isomer of each epoxide has been analysed.

File:Trans beta methyl styrene oxide.jpg

The calculated ¹H spectrum for trans-β-methyl styrene oxide and, the ¹³C NMR spectrum can be viewed here. The methyl group signals have been averaged.

Table 9. ¹H and ¹³C NMR comparisons with lit., trans-β-methyl styrene oxide

Lit. 1H chemical shift (ppm), multiplicity and integration	trans-β-methyl styrene oxide 1H chemical shift (ppm), integration	Lit. 13C chemical shift (ppm)	trans-β-methyl styrene oxide 13C chemical shift (ppm)
7.32-7.22 (m, 5H)	7.49 (3)	137.9	134.98
3.55 (d, 1H)	7.42 (1)	128.4	124.07
3.10 (dq, 1H)	7.31 (1)	128.0	123.33
1.42 (d, 3H)	3.41 (1)	125.5	122.80
	2.79 (1)	59.5	122.73
	1.33 (3)	59.0	118.49
		18.0	62.32
			60.58
			18.84

The ¹H calculated peaks correlate very well with those reported in literature; in an experimental setting (molecule constantly rotating as opposed to static) all of the aromatic ring protons have been considered to be in the same environment but the five most deshielded protons of the predicted spectrum all match up to the literature multiplet representing five protons. The remaining signals and integration values all correspond well, a slight shift observed, again due to solvent effects. A similar situation is seen when analysing the ¹³C NMR data, with comparable chemical shifts although fewer experimental values reported, as a result of overlapping peaks generating multiplets, or carbon environments becoming equivalent due to movement of the molecule.

File:Dihydronaphthalene oxide.jpg

The calculated ¹H spectrum and ¹³C NMR spectrum for 1,2-dihydronaphthalene oxide can be viewed here.

Table 10. ¹H and ¹³C NMR comparisons with lit., 1,2-dihydronaphthalene oxide

Lit. 1H chemical shift (ppm), multiplicity and integration	1,2-dihydonaphthalene oxide 1H chemical shift (ppm), integration	Lit. 13C chemical shift (ppm)	1,2-dihydonaphthalene oxide 13C chemical shift (ppm)
7.33 (d, 1H)	7.62 (1H)	137.1	135.39
7.21-7.14 (m, 2H)	7.39 (2H)	132.9	130.39
7.01 (d, 1H)	7.25 (1H)	129.9	126.67
3.78 (d, 1H)	3.56 (1H)	128.8	123.79
3.65 (t, 1H)	3.48 (1H)	128.8	123.53
2.70-2.65 (m 1H)	2.95 (1H)	126.5	121.74
2.45 (dd, 1H)	2.27 (1H)	55.5	52.82
2.39-2.31 (m, 1H)	2.21 (1H)	55.2	52.19
1.70-1.60 (m, 1H)	1.87 (1H)	24.8	30.18
		22.2	29.06

Computation of the predicted outcome of the epoxidation of 1,2-dihydronaphthalene gives an even better comparison to the experimental product. All of the predicted ¹H chemical shifts are within 0.3 ppm of the literature values, indicating a very successful optimisation of 1,2-dihydronaphthalene oxide structure and subsequent calculation, it also demonstrates how the rigidity of the bicyclic structure leads to a conformation which is more static -less stretching, angle bending etc within the molecule, thus the real example (with total freedom of movement) and the static computed one give such similar spectra. Again the ¹³C spectrum has produced an even closer parallel set of peaks, with the same number of carbon environments reported and very low differences between the two sets of signals. The simulation of 1,2-dihydronaphthalene oxide is in general a better one that that of trans-β-methyl styrene oxide because of greater similarity between the computationally generated naphthalene molecule and a physical one.

Calculated Chiroptical Properties

Enantiomers of trans-β-methyl styrene oxide

Enantiomers of 1,2-dihydronaphthalene oxide

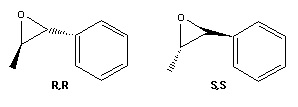
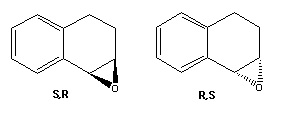
Each of the investigated alkenes has mirror-image versions, which although cannot be differentiated by NMR analysis can be identified through their optical rotation; each will rotate a plane of polarised light in opposite directions, by the same amount. Trans-β-methyl styrene oxide has R,R and S,S configurations, 1,2-dihydronaphthalene oxide has R,S and S,R. The literature value for trans-β-methyl styrene oxide is reported at [α]²⁵_D = +44.3° for the R,R enantiomer, and equivalent in magnitude yet negative for the S,S enantiomer, this is relatively similar to the computed value of 62.6°, the sign being of greatest importance, and revealing that the computationally generated molecule is the R,R enantiomer. The large difference in numerical value is again due to the limitations of predicting properties using computational methods, which is most accurate for α values above 100°, and very sensitive to conformational change. Dihydronaphthalene has a contrasting outcome, the calculated value of -134° differs from the magnitude of literature value ([α]²⁵_D = +129° by a less substantial amount due to the greater accuracy in calculation as the values are so large, and because differences in conformation are likely to be less because of the rigidity of the molecule. The assignment of configuration of the computed molecule is therefore the S,R enantiomer.

Computationally Generated Transition States to Determine Enantiomeric Excess

The relative energies of transition states in the aforementioned catalytic epoxidation reactions will determine unconditionally the preferentially formed enantiomer, and by what enantiomeric excess. By analysing the free energy of transition state the reaction pathway can be determined as it will always follow the lowest energy route; a kinetic phenomenon meaning that the major product of the reaction (which can be determined from the structure of the transition state) can be predicted. Shi catalyst, in its catalysis of trans-alkene epoxidation reactions, has been analysed in terms of the transitions states formed with trans-β-methyl styrene, which could proceed via eight different transition states. Whether the Re or Si face of the alkene is adjacent to the catalyst (designated according to the Cahn-Ingold-Prelog rules for assignation of absolute configuration) , which oxygen atom of the activated dioxirane complex is transferred to the alkene, and whether the phenyl ring of trans-β-methyl styrene is aligned in and endo- or exo- fashion to the fructose ring of Shi catalyst are the three factors, each with two possible outcomes, which need to be taken into consideration.

Table 11. Gibbs free Energies of Shi-trans-β-methyl styrene transition states

	R,R epoxide-forming transition states	S,S epoxide-forming transition states
1	-842759.74	-842757.23
2	-842757.85	-842755.92
3	-842764.13	-842760.99
4	-842766.01	-842761.62

The Gibbs free Energies of all eight possibilities are summarised in Table 11, energies in kcalmol^-1. From this analysis it can be seen that the R,R transition state 4 is the lower in energy, the and both seem to be presenting the same face of the alkene, and reacting with the same oxygen atom of the dioxirane functional group, with a difference in endo-/exo- positioning of the phenyl ring relative to the Shi catalyst. The difference in Gibbs Free Energy of these has been calculated (-18.35 kJmol^-1) in order to evaluate the distribution between the two enantiomers, in other words, the enantiomeric excess. Using Equation 1 the equilibrium constant is calculated which is defined as the ratio of concentrations For the purpose of this calculation, ΔG has been designated G(R,R) - G(S,S), hence K = [R,R]/[S,S].

Equation 1. ΔFailed to parse (syntax error): {\displaystyle ΔG = -RTlnK}

This gave a value of K = 2.243, transformed into an enantiomeric excess using Equation 2. $ee=\frac{(R,R-S,S)}{(R,R+S,S)}\times 100$

This gave an enantiomeric excess of 38.4%, in favour of the R,R isomer, as expected from the transition state relative energies. The jmol 3D images suggest that the R,R epoxide-forming transition state has fewer steric clashes between the phenyl ring and the fructose ring-hydrogens, which a possible explanation for this pathway being favoured.

Table 12. Gibbs free Energies of Jacobsen-1,2-dihydronaphthalene transition states

	S,R epoxide-forming transition states	S,R epoxide-forming transition states
1	-2146943.26	-2146936.99
2	-2146938.87	-2146937.30

The 1,2-dihydronaphthalene epoxidation was chosen for examination of the Jacobsen catalyst transition states in order to continue the investigation into this reaction, as a fixed cis-alkene the reaction should proceed with high yield due to the nature of the catalyst geometry. Four potential transition states exist, corresponding to endo- and exo- orientations of the bicycle, each leading to S,R or R,S enantiomers of the epoxide. The energies of these are presented in Table 12. The transition state structures can be seen via these links, and . Again the Gibbs Free Energy difference has been calculated between the lowest energy transition states for each enantiomer, with a result of -23.81 kJmol⁻¹. Using Equations 1 and 2 gives an equilibrium constant, K = 2.85, which translates into an enantiomeric excess of 48.1% of the S,R configuration. This is confirmed by an examination of the literature which reveals this selectivity to be a result of dihydronaphthalene presenting only its Re face to the Jacobsen catalyst, to minimise steric repulsion. Even bulkier alkene substituents would improve the enantio-selectivity of the epoxidation.

Investigating Non-covalent Interactions in the Transition State

So far in this investigation only formal and partial bonds (in the transition state) have been considered, here non-covalent interactions are also computed in the search for a rationalisation of the stereoselectivity between alkene and catalyst in the transition state. The lowest energy Shi-trans-β-methyl-styrene transition state has been chosen. Non-covalent interactions comprise hydrogen-bonding, electrostatic interactions, and attractive van der Waals forces; including this in analysis of the transition state gives a fuller picture of the interactions, and a more localised breakdown of the energetics of the structure, than the overall free energy. As seen in the picture below several potential isosurfaces can be seen between adjacent areas of the molecule. A colour spectrum ranging from blue (strongly attractive) to red (strongly repulsive) reveals the nature of the non-covalent interactions.

Orbital

Mainly green/blue-green, the interactions are favourable illustrating why the reaction follows a pathway through this, low energy, transition state. Very large areas of attraction can be seen between the substrate and catalyst, in particular between the closest oxygen atoms of the five-membered rings and hydrogens on the methyl, alkene and ring parts of the trans-β-methyl-styrene; likely to be representing hydrogen bonding due to fulfillment of the specific electronegativity requirements for this interaction, and its great stabilising effect. The quantity and specificity of the locations of this hydrogen bonding, acting concertedly, provides a feasible explanation for the stereoselectivity of this transition state pathway. There are also several favourable interactions within the Shi catalyst itself, attractive van der Waals forces between hydrogen atoms, and another hydrogen bond between 1,3-axial hydrogen and oxygen substituents on the fructose ring. All of these greatly outweigh the destabilisation which can be seen in the centre of each ring system of the transition state. The multicoloured oval-shaped isosurface indicates the site where the new bond is forming and thus ignored.

Investigating the Electronic Topology within the Active-Site of the Transition State

The transition state between Shi catalyst and trans-β-methyl-styrene has been further examined using Quantum Theory of Atoms in Molecules (QTAIM), complementary to the Gibbs Free Energy and NCI analysis as it takes into account both covalent and non-covalent interactions. Looking at the electronic distribution distribution, QTAIM identifies points corresponding to several different types of interaction, Bond Critical Points are shown as yellow spheres in the image, representing regions where electron density is at a maximum value, while those with dotted lines depict non-covalent interactions. Six of these weaker interactions (aside from the short, central dotted line between oxirane O and a substrate C) exist between the alkene and catalyst as seen on the right. All of these bar one are attractive van der Waals forces between hydrogen atoms on the two molecules; the remaining dotted line shows hydrogen bonding to an oxygen atom on one of the five-membered rings of the catalyst, substantiating the evidence seen for this in the NCI analysis. These multiple cooperative interactions are almost definitely the rationale behind this transition state forming in this specific conformation; a contribution further to sterics which eplains the enantiomeric excess seen in this range of catalytic epoxidations, although the QTAIM analysis seems to indicate a greater role for other electrostatic interactions as well. The shortest central interaction shows the initiation of bond forming between an oxirane oxygen and the alkene carbon atom furthest from the aromatic ring, implying that this bond is the first formed in epoxidation, possibly as it is sterically more accessible.

Potential Additional Alkenes for Investigation

Pulegone Oxide

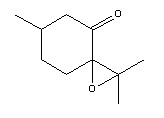
In order to extend the analysis a search was conducted for further alkenes which would produce epoxides which also have easily measurable optical rotation. One such alkene is Pulegone, as a tetra-substituted alkene epoxidation using Shi and Jacobsen catalysts could be compared, as there would be a preference for neither. Pulegone oxide has a reported literature optical rotation of [α] = +10.28° and is a readily available reagent.