Rep:Mod:custardium2802
Module 3
Cope Rearrangement Tutorial
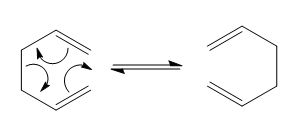
Below is shown the reaction scheme for the Cope rearrangement. This is a [3,3] sigmatropic rearrangement of a 1,5 diene that happens in a concerted manner when the reactant is heated. This reaction involves 6π electrons and follows the 4n+2 rule for aromaticity.
So as to study this reaction, first the possible conformations of the reagent must be optimised, so as to determine which conformer is the most energetically favourable. However, this does not mean that the most energetically favoured one is neccessarily the one that goes on to rearrange; this merely means that this would be the conformation in which the structure is most likely to be found. Then, the possible transition states must be determined and compared.
| Conformer | Structure | Point Group | Energy (hartrees) HF/3-21G |
Relative Energy (kcal/mol) | Energy (hartrees) DFT/6-31G |
Sum of electronic and zero point charge energies at 0K | Sum of electronic and thermal energies at 298.15K and 1atm | Sum of electronic and thermal enthalpies (correction for RT) | Sum of electronic and thermal free energies (entropic contribution to free energy) | Changes in Geometry | |||
| gauche1 |
|
C2 | -231.68772 | 3.1 | -234.55582 | -234.412188 | -234.405138 | -234.404194 | -234.443019 | C=C 1.3158Å to 1.33785Å; C-C: 1.5148Å to 1.5132Å; chain ends distance: 3.515Å to 3.57154Å | |||
| gauche2 |
|
C2 | -231.69167 | 0.62 | -234.55868 | -234.415297 | -234.408051 | -234.407107 | -234.407107 | C=C:1.31564Å to 1.33778Å; C-C: 1.55077Å to 1.55437Å; =C-C: 1.50832Å to 1.50756Å; C=C-C: 124.974o same; chain ends: 4.391Å to 4.5313Å | |||
| gauche3 |
|
C1 | -231.69266 | 0.00 | -234.55934 | -234.415744 | -234.408572 | -234.407627 | -234.447178 | C=C: 1.3163Å to 1.33835Å; =C-C: 1.50756Å to 1.50747Å; C-C: 1.553Å to 1.55657Å; =C-C-C 111.773o to 113.327o</sup. | |||
| gauche4 |
|
C2 | -231.69153 | 0.71 | -234.55849 | -234.414836 | -234.407630 | -234.406686 | -234.445763 | C=C: 1.31642-1.3386Å; =C-C 1.50984 to 1.50827; C-C 1.55533 to 1.55937; =C-C-C 112.388 to 113.999o | |||
| gauche5 |
|
C1 | -231.68962 | 1.91 | -234.55714 | -234.413436 | -234.406340 | -234.405396 | -234.444529 | C=C: 1.31667 to 1.33869Å; =C-C 1.516 to 1.513Å; C-C 1.54571 to 1.5473Å | |||
| gauche 6 |
|
C1 | -231.68916 | 2.20 | -234.55842 | -234.413279 | -234.406162 | -234.405218 | -234.444385 | C=C: 1.3158 to 1.3381Å; =C-C: 1.513 to 1.5115Å; C-C 1.543 to 1.545Å; =C-C-C 113.329o to 114.468o | |||
| anti-1 |
|
C2 | -231.69260 | 0.04 | -234.55977 | -234.416315 | -234.409050 | -234.408105 | -234.447220 | C=C 1.3161 to 1.33818Å; =C-C 1.5089 to 1.5029Å; C-C 1.5523 to 1.5545Å; =C-C-C 111.373o to 112.682o | |||
| anti-2 |
|
Ci | -231.69254 | 0.075 | -234.55970 | -234.416237 | -234.408945 | -234.408001 | -234.447855 | C=C: 1.3163 to 1.3382Å; =C-C 1.5091 to 1.50714; C-C 1.5527 to 1.555; =C-C-C: 111.642o to 112.642o | |||
| anti-3 |
|
C2h | -231.68907 | 2.25 | -234.55771 | -234.414102 | -234.406985 | -234.406041 | -234.444460 | C=C: 1.316 to 1.3385Å; =C-C 1.514 to 1.511; C-C 1.535 to 1.5340Å; =C-C-C: 114.788o to 115.470o | |||
| anti-4 |
|
C1 | -231.69097 | 1.06 | -234.55881 | -234.415255 | -234.408058 | -234.407114 | -234.446573 | C=C: 1.316 to 1.3552Å; =C-C 1.509 to 1.54Å; C-C: 1.543 to 1.54; =C-C-C 110.883o to 109.471o |
In none of the cases did the actual point group change when the molecule was reoptimised, using a more thorough basis set. The HF optimisations found that it was the gauche-3 conformation with the lowest energy, however the DFT optimisations found that it was in fact the anti-1 that had the lowest energy. All of the calorie calculatations were performed with respect to the lowest energy conformations.
Transition State
This concerted pericylic reaction has been found to proceed with three possible transition states: loose boat, loose chair and a diradical tight-chair Delvar-type intermediate structure. According to the literature, these have point groups of C2h, C2h and Cs respectively 1 This was not what was found here, as the boat transition state was found to have C2v symmetry. As this reaction proceeds with 6π electrons, obeying the 4n+2 rule the transition state must be Hueckel, proceeding via suprafacial rotation only.
To generate the first transition state, an allyl of the molecular formula CH2CHCH2 was optimised, using the HF method and the 3-21G basis set. This optimised fragment was then duplicated in another window and the two fragments were oriented into a chair conformation. The distance between the two fragments was made to be 2.2Å. This molecule was then optimised and the frequencies were found, using the HF method and the 3-21G basis set. As this was a transition state, this molecule was optimised to a Berny transition state, with force constants calculated once. Care was taken to imput opt=noeigen, so as to stop the program from crashing after encountering the expected negative vibrational frequencies.
The optimised structure is shown below
| Structure- Chair | Electronic energy (HF/3-21G) at 0 K | Sum of electronic and zero-point energies at 298.15 K(HF/3-21G) | Sum of electronic and thermal energies (HF-3-21G) | Electronic energy (B3LYP/6-31G*) | Sum of electronic and zero-point energies at 0 K (B3LYP/6-31G) | Sum of electronic and thermal energies at 298.15 K(B3LYP/6-31G) | |||
|
-231.619322 | -231.466701 | -231.461341 | -234.505427 | -234.362621 | -234.356705 |
The distance between the fragments was initially given at 2.02Å. All of the C-C bond lengths were given as 1.389Å. The fragments were directly over each other and the angle between within the allyl fragments was 120.492o
An imaginary frequency was found at -818.03cm-1, confirming that this was indeed a transition state. When this vibration was animated, it showed the two fragments moving towards each other in a concerted manner. This transition state has a C2h point group.
This molecule was then constrained so as to make the fragments be 2.2Å apart and then to optimise the rest of the molecule as usual. This optimisation gave C-C bond lengths of 1.381Å.
The constrained transition state was then unfrozen, so that the fragment distance could take the most optimal length. This was found to be: 2.02Å.
Boat Transition State
The fully optimised anti-2 structure from before was used to generate a boat transition state. This was done, by copying the optimised structure into a new molgroup, then adding another molecule to this molgroup. The result was in the form of two molecules in the same window.
This calculation failed, as it produced a transition state reminicent of the previous chair conformation. This is because the program did not take the possible rotation about the bonds into account; it simply translated the allyl fragments. The checkpoint file gave the following structure.
Pentahelicene |
So as to rectify this error, the rotation of the bonds was done for the program and the structures were cleaned.

Now a transition state was computed, using a different method to previously: the QTS2 method. This method works, by generating an intermediate between the imputed reagent and product. This approach differed significantly from the previous method, as a guess transition state was not actually constructed in a window and then optimised with the TS (Berny) method. This is why the numbering of the atoms had to be exactly right, because otherwise the program would imput the wrong coordinates.
| Structure- Boat | Electronic energy (HF/3-21G) at 0 K | Sum of electronic and zero-point energies at 298.15 K(HF/3-21G) | Sum of electronic and thermal energies (HF-3-21G) | Electronic energy (B3LYP/6-31G*) | Sum of electronic and zero-point energies at 0 K (B3LYP/6-31G) | Sum of electronic and thermal energies at 298.15 K(B3LYP/6-31G) | |||
|
-231.602802 | -231.450929 | -231.445300 | -234.493065 | -234.351356 | -234.345053 |
The bond lengths were 1.381Å for the C-C bonds and the distance between the fragments 2.14Å. This structure is entirely eclipsed.
This transition state has C2v symmetry and -231.6028a.u. of energy. This is certainly a transition state, as it has a negative vibrational frequency at -839.959cm-1. The animated vibration shows the fragments approaching each other.
IRC
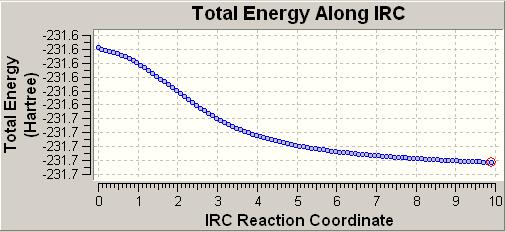
The optimised transition states were then used to perform a further calculation- the IRC (intrinsic reaction coordinate), so as to be able to follow the reaction path. This is done, by taking a set number of steps (initially set at 100) in the forward direction. The IRC function optimises the structure at each stage of the reaction. The calculation is usually performed in both directions, however as this reaction is symmetrical, only the foward direction is needed. The forward direction is defined as being the one in which the transition vector (the direction in which the reactant goes to the transition state) is pointing when the majority of the phase is positive.2 This was done, by using the HF method and the 3-21G basis set.
Once the calculation was completed, the output was checked to make sure that the actual energy minimum had been reached. In most cases, the minimum will not have been reached, so the lowest energy conformer was selected and then reoptimised.
Boat IRC
This was directly set to 100 maxcycles and was sent to scan. The following plot was given:
The lowest energy conformer was initially found to correspond to the gauche 2 structure. The optimised version of this structure was found to be similar in geometry, as well as in energy to the anti-2 structure seen previously. This stucture has an energy of -231.69266a.u. This must mean that it is the anti-2 conformer that undergoes sigmatropic rearrangement, via the boat transition state.
Pentahelicene |
| Structure- anti 2 | Electronic energy (HF/3-21G) at 0 K | Sum of electronic and zero-point energies at 298.15 K(HF/3-21G) | Sum of electronic and thermal energies (HF-3-21G) | Electronic energy (B3LYP/6-31G*) | Sum of electronic and zero-point energies at 0 K (B3LYP/6-31G) | Sum of electronic and thermal energies at 298.15 K(B3LYP/6-31G) | |||
|
-231.69254 | -234.55970 | -234.416237 | -234.408945 | -234.408001 | -234.447855 |
Chair IRC
The same was done for the chair transition state. This gave the following plots:
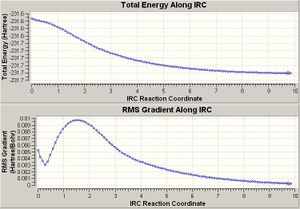
The structure at the far end of the plot (the lowest energy conformation) was then reoptimised. The resulting structure had an energy of -231.69166a.u.
Pentahelicene |
According to the structure and the energy, this optimised structure ressembles the gauche-2 structure. This would mean that when this sigmatropic rearrangement goes via a chair transition, it is the gauche-2 structure that rearranges itself into the chair transition state.
According to the literature, both of these transition states are possible. However, given the structures that the IRC calculations traced the reaction back to, one of these will be higher in energy than the other. This would imply that one of the intermediates is more likely than the other, as there will be more of the conformer that has a lower energy. In this case, that would imply that the reaction is more likely to proceed via the chair transition state than it is to go via the boat.
Activation Energies
*1 hartree = 627.509 kcal/mol
Summary of activation energies (in kcal/mol)
| HF/3-21G | B3LYP/6-31G* | Expt. | |
| at 298.15K | at 298.15 K | at 0K | |
| ΔE (Chair) | 45.94 | 34.056 | 33.5 ± 0.5 |
| ΔE (Boat) | 56.311 | 52.79 | 44.7 ± 2.0 |
The activation energies match well for the chair, but not for the boat. The boat transition state was then reoptimised a further two times, yet the result remained the same.
References
The Diels-Alder Cylcoaddition
The reaction that shall be studied is the following that takes place when the reagent is heated:
This again is a reaction involving 6п electrons, which means this this too will have a Hueckel transition state with only suprafacial components.
2.1 Generation of MOs for cis-butadiene
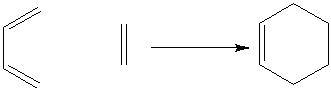
First of all, the molecular orbitals of cis-butadiene were calulated and then the HOMO and LUMO orbitals were visualised, so as to explain the approach the diene takes when the two molecules react. This will help when determining how the transition state for this reaction looks. It must be noted that following optimisation, the molecule was no longer completely flat.
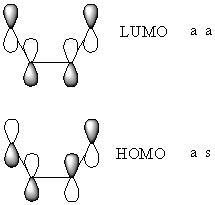
Stereospecific concerted reactions are only allowed when the HOMO/LUMO pairs that interact have the same symmetrical properties, as otherwise they would not overap. The HOMO in this case is that of the cis-butadiene and the LUMO is that of the alkene.
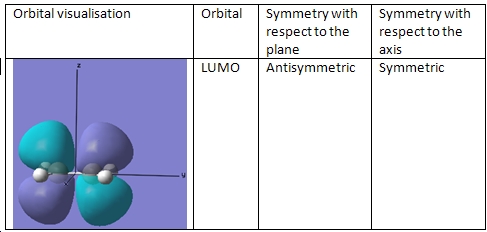
Ethene Molecular Orbitals
As can be seen, the symmetries of the HOMO/LUMO pair are the same, meaning that the reaction between the two molecules can proceed in a stereospecific and concerted fashion.
The reason for which the endo product is favoured over the exo product is because of the secondary orbital overlap that is more favourable in the case of the endo than it is in the exo.
2.2 Generation of the Transition State
To see how the reaction proceeds, the possible transition states must be compared and analysed. First of all, they must have the right approach to allow orbital approach and secondly, they cannot be too high in energy.
In this exercise, the transition state of this reaction will be generated. This will be done, by optimising the two reactants separately and then copying them into the same page and orienting them in an enevelope-type structure. This is then optimised, using the Hartree-Fock method and using the 3-21G basis set.
To find out whether this is a transition state, or not, the optimised molecule will then be used to calculate vibrational frequencies. This will show whether the structure is indeed a transition state, or not, as transition states tend to have imaginary negative vibrational frequencies. The negative vibrational frequency does not actually have any physical meaning- it is merely the result of the algorithm with which this program functions. This particular frequency is imaginary, which in this case is expressed by a negative sign in front of the frequency, however the imaginary vibration corresponds to the motion the molecules undergo when the approach to form the bonds. In that way, much can be found out about the reaction dynamics from this simulation of vibrational frequencies. The motion should also be able to tell you whether the formation of the bonds is synchrous, or asynchrous, which will determine whether or not this reaction fits the strict definition as to what constitutes a pericyclic reaction.
Initially, the HF method with the 3-21G basis set was used and a Berny transition state was generated, taking care to enter opt=noeigen into additional keywords to do opt-freq calculations, however, the output did not resemble the imput molecule. To rectify this, the distance between the fragments was set to 2.5 angstroms and the molecule was optimised, using the same method. Then, the outcome of that scan calculation was then modified to "relax" the bond distances, so that the optimised distance between the fragments in the transition state could also be calculated.
The optimised structure is shown below:
Pentahelicene |
The interfragment distance is 2.21Å, which quite different to the distance at which the fragments were originally constrained. The dashed bond length is 1.39Å as opposed to the usual 1.34Å for a double bond and 1.54Å for a single bond, which clearly shows that this is a double bond in formation. The other double bonds in the cis butadiene part of this fragment are also longer than the usual length at 1.37Å, which also shows that these are in the process of making the transition from double to single bond. The ethene portion of the transition state has a bond length of 1.375Å which shows the same thing. 1 The van der Waal radius of carbon is 1.702 and the distance between the fragment is 2.21Å. This clearly shows that there is significant overlap between the adjacent carbon atoms on the fragments, which confirms that this is a transition state, as this would mean that the carbon atoms are occupying each other's space.
The fact that this is indeed the optimised transition state is shown by the fact that there is a negative vibrational frequency at -817.77cm-1 that shows the motion of the two fragments approaching each other. This shows that this particular cycloaddition is indeed a concerted reaction, so it does fall under the category of percyclic reaction. The next frequency is positive and occurs at 166.624cm-1. This vibrational frequency corresponds to the ethene moving left to right.
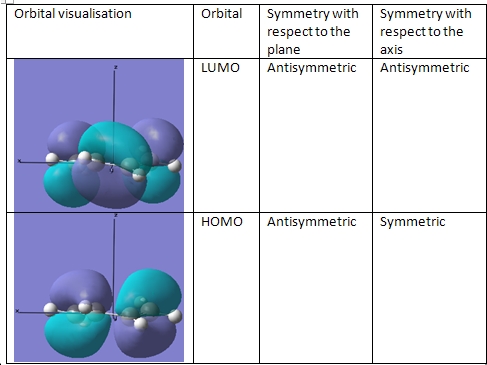
The HOMO was then generated and its symmetry was determined.

2 Element Name list Bond lengths and Radii
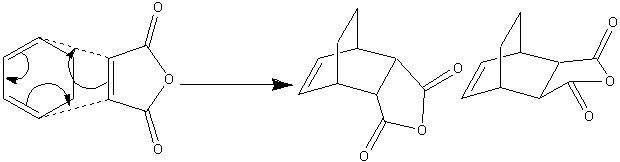
2.3 Study of the Regioselectivity of the Diels-Alder Reaction
In this reaction, the first possible product is 3 exo and the second is 4 endo. However, it is the 4 endo that is most likely to form in this particular reaction. This can only be rationalised with the transition state, as the most favoured transition state is going to be the one that is the lowest in energy. However, this already raises even more questions, as although it is the endo product that is the one that is favoured, the exo product is still formed. As would be assumed, the endo transition state is of a lower energy than the exo transition state, due to the correct orientation that allows the relevant orbitals to overlap. This would mean that the exo state is not oriented in this manner, implying that the orbitals do not overlap well. How does the exo product form, even though the transition state is not of the correct geometry. The fact that it does form implies that the endo exo product is a lot more thermodynamically favoured.
Initially, the transition state was computed, by generating the fragments of the "guess" structure, then using the Hartree-Fock method and 3-21G basis set to do an optimisation and frequency calculation at the same time. This was uploaded as a Berny transition state to SCAN. The problem was encountered when the SCAN had completed- the output looked nothing like the imput, as the molecule had been distorted beyond recognition. For this reason, a different approach was then used to avoid this problem: the imput file was modified to fix the distance between the two fragments at 2.2 angstroms and was then resubmitted to scan. This optimised output file was then modified to unfreeze this distance and was optimised yet again.
The optimised molecules gave negative vibrations that reflected how the fragments approach when they are reacting. This will hopefully give an answer as to just how the exo transition state overcomes its shortcomings in its orientations to react.
Exo Product
Pentahelicene |
This transition state has a distance of 2.26Å between the fragments and has an energy of -605.60 a.u.
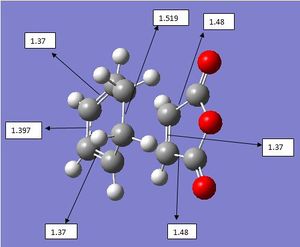

The exo product had a negative vibrational frequency at -647.45cm-1 which shows that this optimised molecule is indeed a transition state. The vibrational motion of this fragment shows that the reaction between the two starting materials is concerted, so this is a truely concerted reaction. However, it must be remembered that the exo product is formed to a lesser extent than the endo product. This can only be rationalised by looking at the orbitals in play.
From this visual representation of the atomic orbitals, it is seen that there are many nodes in the HOMO.
Endo Product
The same was done for the endo product: the transition state was constructed, by modifying the actual endo product. The geometry was first constrained to make the fragment distance be fixed at 2.2Å and then optimised. The difficulty encountered here was that a molecule with two negative vibrational frequencies was generated, which couldn't possibly be correct, even though one of the vibrations showed the movement of the two fragments towards each other. This is because concerted pericylic reactions only have one transition state. So, what was done is the exo output file was copied and the maleic anhydride portion of the transition state was reoriented, so as to make it endo, as it was assumed that the rest of the molecule would then have the correct geometry. The transition state was then optimised as before. Once this calculation was completed, the fragments were unrestrained and reoptimised to give a structure similar to this:
Pentahelicene |
However, this structure was still incorrect, as the problem with there being two negative frequencies persisted (at 611.15 and at -192.94cm-1), despite around ten attempts at reoptimising and reorienting the structure, as well as adding additional keywords, such as opt=noeigentest, which ought to have stopped a further negative frequency from being found.
The animation of the two negative frequencies showed that were these movements combined, this would give the movement of the fragments towards each other in the transition state. The fact that there were two negative vibrational frequencies implied that there was something amiss with the geometry that it failed to correct.
It seemed as though this transition state might be stuck in an energy well- i.e. the optimisation had reached a minimum and so stopped, even though there was another minimum further along. The incorrect structure with its two negative vibrational frequencies was then reoptimised, using the B3LYP method and the 6-31G basis set. The result of this calculation gave somewhat different vibrational frequencies, but there were still two of them, which went to show that the structure was still incorrect. This was then reoptimised again with a 6-311G basis set, hopefully to give a working structure.
This too failed and the job was aborted.
What can be inferred, however is that the endo structure has some constructive overlap of the molecular orbitals that permits this transition state to be stabilied, thus lowering the activation energy of this reaction, whereas as was seen before, the exo product had none, or at most very little stabilisation. This would explain why this reaction primarily gives the endo product. However, what must also be considered, is why the exo product is formed if its transition state is higher in energy than the endo transition state.
So as to find out why the exo product was formed, despite having a transition state of a higher energy, both the endo and the exo products were optimised, using the HF method and the 3-21G basis set. After the initial optimisation, this was then upgraded to the DFT/B3LYP method, using the 6-31G basis set to give a more accurate energy.
The optimised exo product had an energy of -612.5636a.u.; the endo product had an energy of -612.56577. Although these energy differences don't look that substantial, there are 627.509kcal/ mol per hartree. This goes to show that the exo product is more stable than the endo product, meaning that it is the thermodynamically more favoured product and the endo product is the more kinetically favoured product, due to its more favourable transition state. This explains why the exo product even forms.
The next question is: why is the exo form more stable than the endo? This can only be determined, by looking at the molecular orbitals.
When comparing these, it becomes clear that there is more overlap between the combined fragments (atoms 7 and 2 and 9 and 3) in the exo structure than in the endo structure. This would strongly imply that the sigma bond between the joined fragments would be shorter in the exo case than in the endo case. The sigma bonds that joined the two reacants is 1.568Å in the case of the endo structure; in the exo structure it is 1.57Å, significantly shorter.
The fact that the molecular orbitals generated in the transition state do not reflect the stability of the actual product is because the transition state orbitals are not yet fully bonded, so overlap is harder to achieve. It takes more energy to make the reaction go in this way, even if the result is more energetically favourable.