Rep:Mod:csw14TS

Introduction

In this lab, the Gaussian program was used to identify transition states and minima on the potential energy surface of pericyclic reactions. The pericyclic reactions investigated were the [4+2]-cycloaddition, also known as the Diels-Alder reaction, and the cheletropic reaction.

The potential energy surface (PES) is a function that shows the overall energy of the molecule with respect to its configuration. Minima on the PES correspond to favourable, stable configurations of the systems. Generally, there are many local minima on the potential energy surface. However, when perturbed, the system can be optimized further to find the global minimum, or the most stable configuration of the system. Conversely, transition states are high energy configurations that the system can adopt. They appear as maxima on the PES. The molecule corresponding to the transition state is often a transient contorted species.

The gradient at both the minima and transition states is zero with respect to the PES. However, the curvature, or the second derivate of the PES, is different at the two types of points. If the curvature is positive, the point is a minimum. If it is negative, the point is a transition state. The curvature of the PES also relates to the vibrational frequencies of the molecules - thus, transition state structures have a negative frequency.

All structures were initially optimized to the PM6 level. This allowed for faster calculations as this method does not require an atomic basis set to be defined; instead, it relies on empirical data to guess the structures. The structures in exercise 2 were further optimized to the B3LYP/6-31G(d) level. This method uses the density functional theory and gives more rigorous outputs. It is, as a result, more computationally intensive.

Nf710 (talk) 15:12, 10 February 2017 (UTC) Your definition if a TS is a bit confused. How many dimensions are we talking about. A TS is negative curvature in only one of its dimensions.

Exercise 1

In this exercise, the [4+2]-cycloaddition of butadiene and ethene is modelled. The overall reaction involves the dissociation of 2 pi bonds and formation of 2 sigma bonds. The MO diagram of the frontier orbitals of butadiene and ethene and the orbitals of the transition state can be seen below.

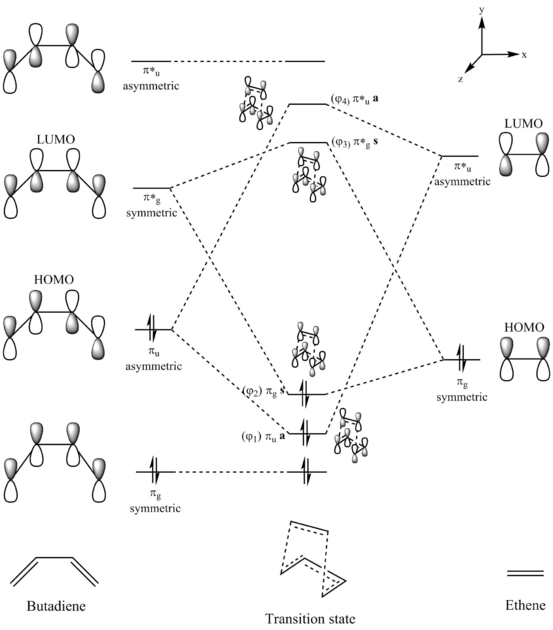
As seen in the diagram, the HOMO and LUMO orbitals of the butadiene and ethene combine to form 4 new transition state MOs. The butadiene and ethene orbitals of the same symmetry combine; the asymmetric butadiene HOMO combines with the asymmetric ethene LUMO while the symmetric butadiene LUMO combines with the symmetric ethene HOMO. As the butadiene LUMO and the ethene HOMO are closer in energy and thus have a larger interaction, the resulting transition state MOs have a larger splitting.

The HOMO and LUMO MOs of butadiene and ethene are shown below.

Butadiene	Ethene
LUMO (MO 12)	LUMO (MO 7)
HOMO (MO 11)	HOMO (MO 6)

The transition state MOs ψ1, ψ2, ψ3, and ψ4 correspond to MO 16, MO 17, MO 18, and MO 19 in the Gaussian computation. They are shown below.

Transition state	HOMO - 1 (MO 16)	HOMO (MO 17)	LUMO (MO 18)	LUMO + 1 (MO 19)

It can be seen from the transition state MOs that the orbitals are combinations of reactant frontier orbitals with the same symmetry. MOs ψ1 and ψ2 were formed from butadiene and ethene orbitals of the same phase, resulting in regions of increased electron density, or bonding interactions, in the transition state. On the other hand, MOs ψ3 and ψ4 were formed from orbitals of different phases, resulting in nodes, or anti-bonding interactions, in the transition state.

Origin of Symmetry Requirements

As stated earlier, symmetric and asymmetric frontier orbitals do not combine with each other, but only with other orbitals of the same symmetry. This symmetry requirement for the formation of molecular orbitals arises from quantum mechanics. The overlap integral S_AB gives the extent of interaction between two orbitals, A and B. It involves the product of a wavefunction and a complex conjugate.

${\mathbf{S}}_{\mathrm{A}\mathrm{B}}=\int {\mathrm{\Psi }}_{\mathrm{A}}^{*}{\mathrm{\Psi }}_{\mathrm{B}}dV$

If both terms in the integral are symmetric or asymmetric, the product will be symmetric and give a non-zero integral. However, if one is symmetric and one is asymmetric, the product will be asymmetric and its integral will be zero. The overlap integral S_AB would thus also be zero, indicating that there is no interaction between the orbitals.

Bond Length Analysis

The C-C bond lengths of butadiene, ethene, and cyclohexene are shown below. The bond lengths are in agreement with typical carbon bond lengths for the respective hybridization modes.

Butadiene	Ethene	Cyclohexene

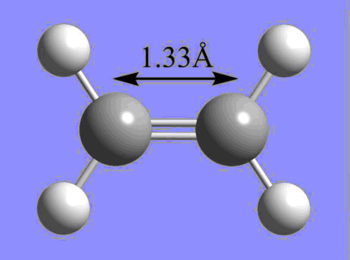
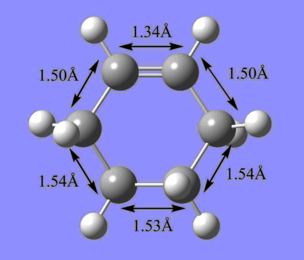
Type of Bond	Typical length (Å)
sp3 C - sp3 C	1.54
sp3 C - sp2 C	1.50
sp2 C - sp2 C	1.34
C Van der Waals radius	1.70

The C-C bond lengths in the transition state are shown below. The bond lengths of the starting materials have become intermediates between C-C single and double bonds. The bond length of the ethene fragment has shortened; the terminal C-C bonds of the butadiene molecule have lengthened and the central bond has shortened. This indicates that electron density is shifting to break the existing pi bonds and form new pi and sigma bonds. The distance between the terminal carbons of the butadiene and the carbons are ethene are less than 2 times the Van der Waals radius of carbon, indicating that bonding interactions are forming between the two fragments.

Transition State

Vibrational Analysis

The vibration of the transition state that corresponds to the reaction path is shown below. The vibration has a negative frequency; because it occurs at a maximum on the potential energy surface, where the curvature is negative, the vibration is also negative. Based on the vibration, it can be seen that the formation of the two new bonds is a synchronous process.

Transition State Vibration

Nf710 (talk) 15:27, 10 February 2017 (UTC) This section was done fairly well, very nice MOs, what was the electron demand? Also your MOs have the wrong symmetry. We state in the script not to use these as it suggests there is a center of inversion which there is not.

Exercise 2

In this exercise, the [4+2]-cycloaddition between cyclohexadiene and 1,3-dioxole is modelled. There are two possible products that can be formed - the endo product and the exo product. The endo product is formed via a transition state where the cyclohexadiene and 1,3-dioxole molecules are overlapping. The exo product is formed via a transition state where the 1,3-dioxole molecule is pointing away from the cyclohexadiene.

The MO diagram of the frontier orbitals of cyclohexadiene and 1,3-dioxole and the orbitals of the transition state can be seen below. While the transition state in the MO diagram shows the overlap that will give the endo product, the frontier orbital interactions and relative energies of the transition state MOs are identical for the transition state of the exo product.

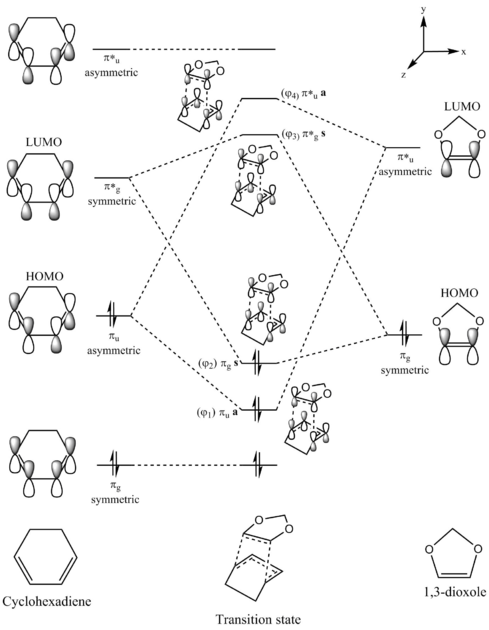
(These symmetry labels are wrong. Just use symmetric/antisymmetric. Not only do they not have an inversion centre, but if they did, your u and g would still be the wrong way around. You need to look up what ungerade and gerade mean Tam10 (talk) 14:10, 8 February 2017 (UTC))

The reaction between cyclohexadiene and 1,3-dioxole is an example of an inverse electron demand Diels-Alder reaction. As the dienophile has electron-donating -OR substituents, the energies of its HOMO and LUMO increase. In this scenario, the interaction between the dienophile HOMO and diene LUMO form the HOMO and LUMO of the transition state.

The new transition state MOs for both the endo and exo product can be seen below. The transition state MOs ψ1, ψ2, ψ3, and ψ4 correspond to MO 40, MO 41, MO 42, and MO 43 for both the endo and exo pathways in the Gaussian computation.

Endo	HOMO - 1 (MO 40)	HOMO (MO 41)	LUMO (MO 42)	LUMO + 1 (MO 43)
Exo	HOMO - 1 (MO 40)	HOMO (MO 41)	LUMO (MO 42)	LUMO + 1 (MO 43)

The HOMO and LUMO of the transition state are both symmetric, indicating that they were formed from symmetric frontier orbitals. The dienophile HOMO and the diene LUMO are symmetric, indicating that they indeed formed the HOMO and LUMO of the transition state. Additionally, the HOMO-1 and LUMO+1 pair are both anti-symmetric, indicating that they were formed from the asymmetric dienophile LUMO and diene HOMO. Thus, the reaction is an example of an inverse electron demand Diels-Alder reaction.

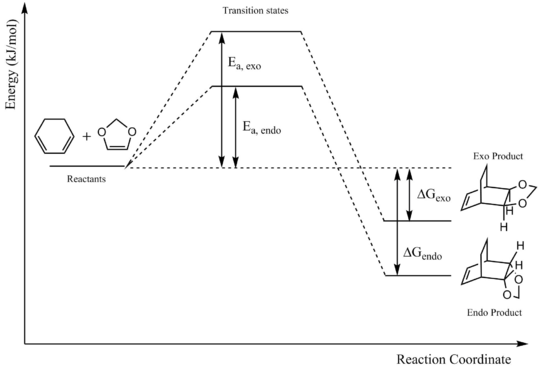
Reaction Profile

The reaction profile of the cycloaddition can be seen below.

Energy gap	Energy (kJ/mol)
Reactants	-1.31x106
Ea, endo	159.82
ΔGendo	67.40
Ea, exo	167.64
ΔGexo	63.81

The endo product is both kinetically and thermodynamically favoured over the exo product. Though it appears be more sterically hindered and thus unstable, the endo transition state may instead be stabilized by secondary orbital interactions, lowering the activation energy barrier. In the HOMOs of the two transition states shown below, it can be seen that there is an interaction between the oxygens of the dienophile and the central carbons of the diene in the endo transition state. The region around the oxygens is out of phase with the rest of the electron density surrounding the dienophile but in phase with the diene; the stabilization provided by the central carbons of the diene may thus have a significant effect in the overall lowering of the transition state energy. This interaction is absent in the exo transition state.

Endo TS HOMO	Exo TS HOMO

Nf710 (talk) 15:35, 10 February 2017 (UTC) Your energies are correct well done and you have come to the correct conclusion. if you look at the sterics the endo is actually less hindered

Exercise 3

In this exercise, the [4+2]-cycloaddition between ortho-xylylene and sulphur dioxide is modelled. Like the reaction in exercise 2, the cycloaddition can result in an endo or an exo product. The subtrates can also undergo a cheletropic reaction, giving a total of three possible products for the reaction between ortho-xylylene and sulphur dioxide.

Like the Diels-Alder reaction, the cheletropic reaction is also a pericyclic reaction. It involves the formation of 2 new bonds to the same atom on one of the reactants. In this case, the xylylene forms 2 new bonds to the sulphur of SO₂.

The reaction coordinates of the endo Diels-Alder, exo Diels-Alder, and cheletropic reactions can be seen below.

Endo	Exo	Cheletropic

It can be seen that bond formation is asynchronous in the Diels-Alder reactions. This may be attributed to the fact that the dienophile is composed of two different heteroatoms. The bond formation is synchronous, however, in the cheletropic reaction as both new bonds are formed with the same heteroatom. It can also be seen that the 6-membered ring of xylylene gains aromaticity over the course of all three reactions. The drive to form an aromatic product may explain the enhanced reactivity of xylylene.

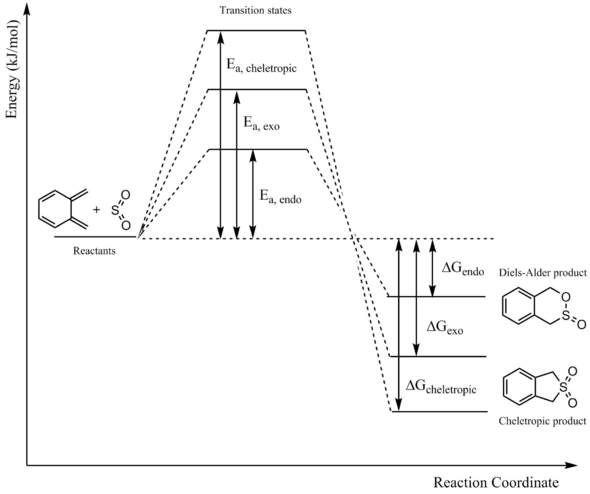
Reaction Profile

A reaction profile with the relative energies of the reactants, transition states, and products can is shown below.

(Nice diagram. Putting values on here would make comparison quicker Tam10 (talk) 14:10, 8 February 2017 (UTC))

Energy gap	Energy (kJ/mol)
Ea, endo	83.43
ΔGendo	97.37
Ea, exo	87.42
ΔGexo	98.00
Ea, cheletropic	105.75
ΔGcheletropic	154.33

(Use signed numbers to indicate the reactions are exothermic Tam10 (talk) 14:10, 8 February 2017 (UTC))

The endo product is the kinetic product for this reaction. Once again, the transition state is most likely stabilized by secondary orbital interactions between the oxygen on SO₂ and the diene. The cheletropic product is the thermodynamic product for this reaction.

Alternative Diels-Alder Reaction

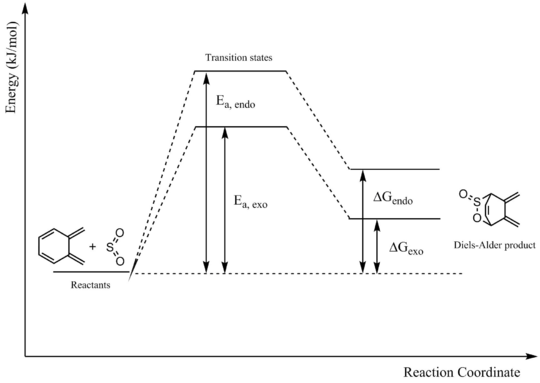
Xylylene has a second diene fragment that can undergo the Diels-Alder reaction with SO₂ to give an endo or an exo product.

The reaction coordinates of the endo and exo Diels-Alder reactions at this site can be seen below.

Endo	Exo

While the reaction is possible, it is both thermodynamically and kinetically unfavourable. As seen in the reaction profile and table of energy values below, the activation energies for both the endo and exo reactions are very high, making them kinetically unfavourable. Additionally, the energies of the products are higher than that of the reactants, making their formation thermodynamically unfavourable. A contributing factor may be that the product does not attain aromaticity like those of the previous reaction.

Energy gap	Energy (kJ/mol)
Ea, endo	121.49
ΔGendo	22.38
Ea, exo	113.65
ΔGexo	17.92