Rep:Mod:crumblanium2802
BH3
Pentahelicene |
* What is the optimised B-Cl bond distance? 1.65Å * What is the optimised Cl-B-Cl bond angle? 120o * What is the file type? .log * What is the calculation type? FOPT * What is the calculation method? 3-21G * What is the basis set? LANL2MB * What is the final energy in atomic units (au)? -26.46a.u. * What is the dipole moment? 0.00Debye * What is the point group of your molecule? D3H * How long did your calculation take? 6 sec
The fact that the screenshot does not show any actual bonds as we know them (i.e. lines between atoms) is because Gaussian rationalises bonds in terms of how close the atoms are to each other and in terms of which atoms are involved in the interaction. From this, Gaussian can make a good approximation as to just how strong the interactions between the atoms are.
The optimisation function works, by finding the lowest possible energy configuration the molecule can have. This is done by the program assessing the bond distance equilibrium, so that nuclear repulsion is balanced out by the favourable electrostatic interactions. The only drawback with this method is that sometimes the molecule can get stuck in an energy well, where the program has calculated a low energy and stays with this configuration, despite the fact that there may be an even more energetically favourable configuration of the molecule. This is because the program goes through all possible configurations and declares the job finished as soon as the gradient confirms there is a minimum. For the actual minimum to be established, the program would have to go through higher energy configurations before reaching another minimum, which it doesn't do, because otherwise it would have to continue ad finitum ed ad nauseum.
Find Information about BCl3
* What is the optimised B-Cl bond distance? 1.775Å * What is the optimised Cl-B-Cl bond angle? 120o * What is the file type? .log * What is the calculation type? FOPT * What is the calculation method? RB3LYP * What is the basis set? LANL2MB * What is the final energy in atomic units (au)? -69.44a.u. * What is the dipole moment? 0.00Debye * What is the point group of your molecule? D3H * How long did your calculation take? 16 sec This molecule was then optimised, using the .log file to give the following graphical representations:
Pentahelicene |
The gradient describes how steep the slope is and what direction it goes it. It is formally described as dy/dx.
Draw your own Molecule
The molecule I chose is AlF3. The information obtained from the summary is the following:
* What is the optimised B-Cl bond distance? 1.65Å * What is the optimised Cl-B-Cl bond angle? 120o * What is the file type? .log * What is the calculation type? FOPT * What is the calculation method? RB3LYP * What is the basis set? LANL2MB * What is the final energy in atomic units (au)? -297.11a.u. * What is the dipole moment? 0.00Debye * What is the point group of your molecule? D3H * How long did your calculation take? 13 sec
Pentahelicene |
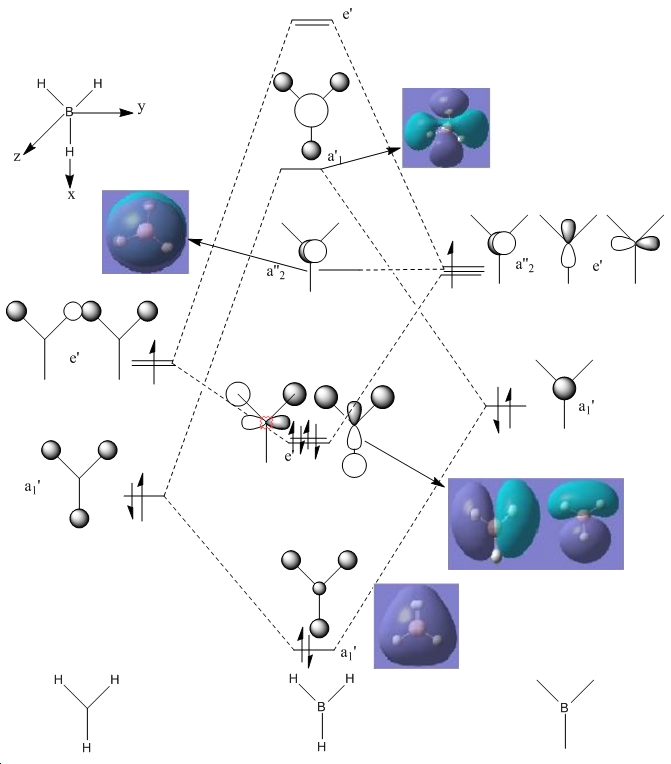
BH3 MOs
Using Gaussview, the occupied molecular orbitals were generated. The program did this, by solving the Schroedinger equation and using this data to generate pictorial representations of the electron density around the atoms. This was done for the occupied orbitals, as well as for the LUMO. However, it must be noted that these calculations are only approximations, as Gaussian cannot fully account for the electron-electron repulsion. So as to try to approximate it, it includes it in the Hamiltonian operator in the Schroedinger equation, without including it in the actual wavefunction product. This means that the wavefunctions generated have no electron-electron interaction. Including it in the Hamiltonian tends to overestimate the energies.
This is the orbital that is lowest in energy. This is the s-orbital of the boron. As can be seen from the energy of this orbital, it is so low that it would not be able to take part in any kind of interaction (-6.73a.u.). This is why it is generally omitted when considering the bonding in the molecule, which is why it is not included on the next image that combines calculated molecular orbitals with the schematic MO diagram. As it is fully symmetrical, it has a'1 symmetry
This is the first bonding interaction. All of the s orbitals of the H's and the boron are overlapping in-phase, resulting in a strong σ interaction. The energy of this orbital is -0.57. This orbital too is fully symmetrical, so it also has a'1 symmetry.
The next two orbitals are degenerate in nature. This is clearly seen, as they both have the same energy (-0.434a.u.) they have e'symmetry.
The orbital below is the LUMO interaction. As this orbital is not filled, it is a lot more diffuse than the others. This orbital is a non-bonding interaction from the pz orbital of the boron. This orbital is higher in energy than the others (-0.076a.u.), yet as can be seen from the sign of the energy, any electrons in that orbital would result in a stabilising force. This is why BH3 is a Lewis acid.
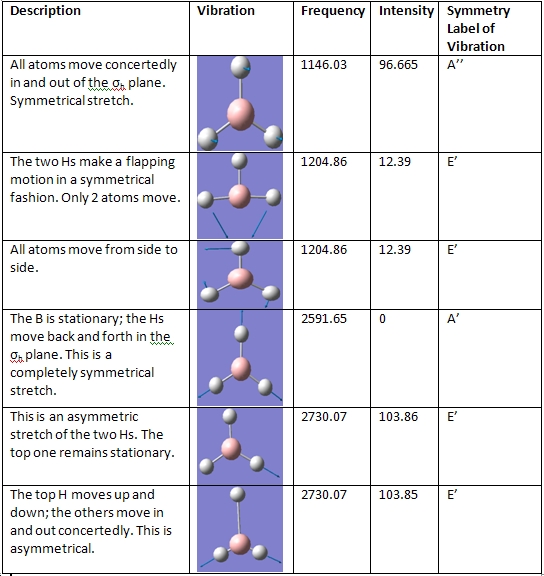
BH3 Frequencies
When comparing these quantitative values with the qualitative MO diagram, they actually match exceptionally well. If anything, the computed values do work better- particularly when explaining why BH3 can accept electrons so easily, which as one would already assume the qualitative method cannot do as well. The actual structures of the MOs do however vary to some extent- some more than others.
Cis and Trans Isomerism
The cis and trans isomers of the molybdenum complex Mo(CO)4L2 were optimised twice to give their geometry. First, the B3LYP method with the LANL2MB basis set was used, then the B3LYP method with the LANL2DZ basis set was used to further optimise the optimisation.
The geometries of these structures were then analysed:
Pentahelicene |
Pentahelicene |
Both of these have C1 symmetry, which shows that they are not symmetrical at all.
Unfortunately, it was impossible to upload the structure to D space, so an objective comparison with an already-existing molecule could not be made.
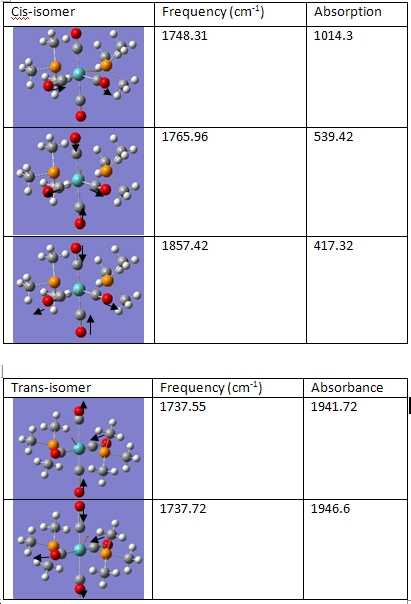
The cis molecule had an energy of -773.3469a.u. and the trans molecule had an energy of 773.3439 a.u. This gives an energy difference of 0.003 a.u. which is 7.87KJ/mol difference.
When the IR frequencies were compared, it was found that the trans- isomer had one major peak and the cis- isomer had that same peak, as well as another smaller peak slightly beyond it at 1857.42cm-1. This can be rationalised in the following manner: the main peak in the IR spectrum is formed by 2 CO stretches. As the frequencies generated by these vibrations are so close to each other, they make the IR spectrum look like this is just one peak, even though it is actually made up of two peaks that are superimposed on each other. The trans- conformation of this molecule has this major peak, yet is lacking the smaller peak that only the cis- isomer has.
Although it looks like these ought to be the same vibrations, as their frequencies are similar, they are actually not the same. This would explain the difference in frequencies. However, when the third frequency is compared with the trans- isomer's vibrations, it is found that there it would be possible to have a fully symmetric stretching frequency for the trans isomer. The reason why it does not show up despite the fact that its cis analogue does is because its symmetry is such that this stretch would not induce a change in dipole. Without a change in dipole, the vibration will not be detected in an IR spectrum
NH3
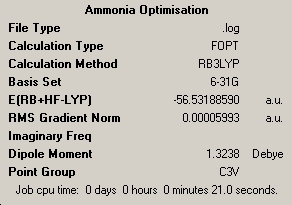
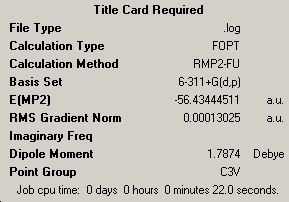
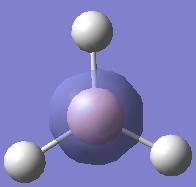
Part 1- Ammonia Symmetry NH3 was drawn and optimised, using Gaussian. The method used was B3LYP and the basis set used was 3-21G. This resulted in the following molecule:
Pentahelicene |
This molecule has C3v symmetry.
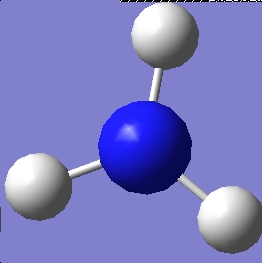
This molecule was then modified, so that one of the bond lengths became 1.01Å, instead of 1.006 which effectively destroyed the symmetry. This molecule was then optimised, ignoring the symmetry to give yield to the following molecule with C1 symmetry.
Pentahelicene |
An already-existing file was then used to create another form of ammonia that had a different symmetry (http://www.ch.ic.ac.uk/hunt/teaching/teaching_comp_lab_year3/nh3_highsym.txt). The molecule generated by this file before optimisation had a "dummy" atom, so as to restrict the geometry.
Pentahelicene |
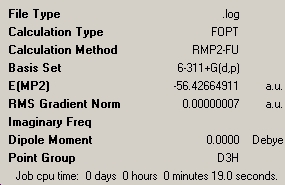
As can be seen from the properties of these molecules, the difference in symmetry has had an effect on them. For one, the geometry of them has been changed, which has resulted in the fact that they have different energies. As can be seen from the summaries of these jobs, the more symmetry elements a structure has, the longer it takes for the calculation to run, as the higher the symmetry, the larger the matrix of the molecule will be, which means that it will take longer to compute the molecule. High-symmetry molecules will simply take a lot more time on the processor.
During optimisation, it is possible for a molecule's symmetry to be broken if this results in a more stable conformation- that is if the symmetry has not been constrained.
Whether or not a molecule adopts a certain shape depends on how energetically favourable it is. After comparing three possible geometries of ammonia, it is concluded that it is indeed the first one (C3v symmetry) that is the most energetically favoured, as it is the one that is closest to 0. This in itself is already a breakdown of the Born-Oppenheimer approximation that takes electrons to be so insignificant that their part to play in molecular dynamics can be ignored. The fact that this molecule has been shown to take on this shape shows that this approximation is not applicable in all cases. The other two isomers have the energies -148424 KJ/mol (C1 symmetry) and 148500 KJ/mol (D3h). These differences in energy may not look particularly substantial in Hartrees, yet they are quite substantial in joules.
The change in symmetry means that there is a change in electronic configuration, as only the orbitals with the same symmetry can combine. From what can be seen from the overall energy calculations, some configurations are more stable than others, meaning that some geometries will be favoured over the others. However, ammonia is a particular case, as it can undergo quantum tunelling, which results in the flipping of the molecule. Simply explained, this by the electron being able to escape (tunnel) from the infinitely high potential walls that are caused by the attractive force of the nucleus. This property has the potential to be extremely useful in the development of "Q-Bit" computers.1
1 [1]
Part 3
These outputs were then compared with what happens when the method, as well as the basis set is changed. Below is the image of the molecule after optimisation:
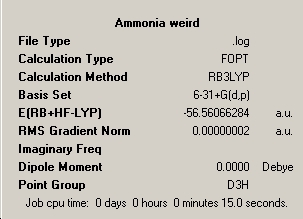
An already-existing file was used to generate an NH3 molecule with a D3h symmetry. This again had a "dummy" atom, so as to restrict the symmetry. This was optimised, using the MM2 method and the 6-311G basis set. The results of these two calculations were compared with the previous ones.
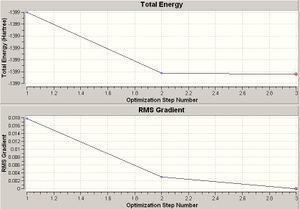
Another file was used to follow the motion of a C3v NH3 molecule becoming D3h. This could then be animated to show the flapping motion of the molecule as the point group changes from one to another. This then gave two graphs; one of them showed how the energy varied, as the molecule "flapped"; the other was a graph of the RMS gradient.
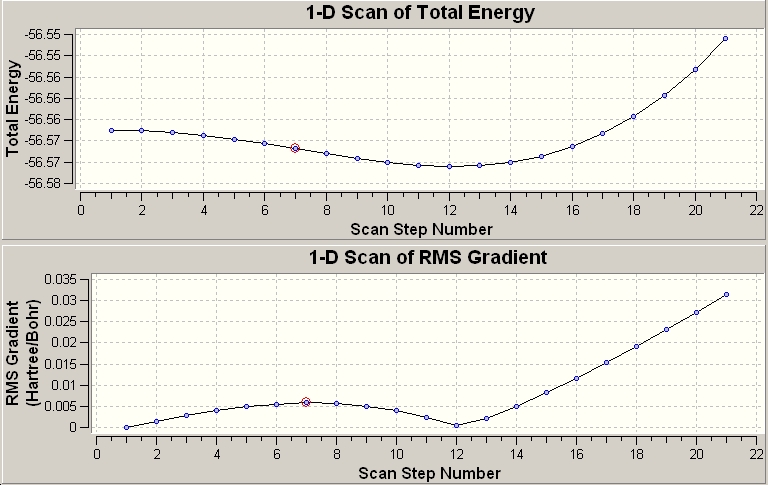
The time taken for the calculations was generally longer than previously. This is because a different basis set was used i.e. a different set of functions was used to approximate an atomic orbital. The fact that it took longer means that more a more complex set of functions was used to map the atomic orbitals, which accounts for the fact that the calculations took longer.
The energy difference between the C3v and the D3h conformations is 20.47KJ/mol. This is in reasonable agreement with literature values, yet it is still rather approximate.1 This means that for the NH3 molecule to invert, it needs an energy imput of 24.3KJ/mol.
The energies of the C3v NH3 changed hugely when the basis set was changed. Indeed, the former is 255.8KJ/mol higher than the latter. This just shows how important it is to have an accurate basis set.
Vibrations
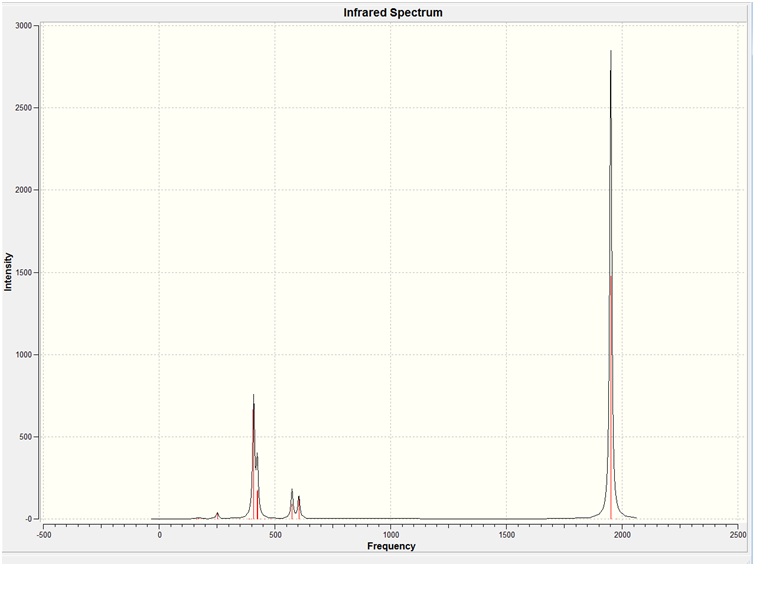
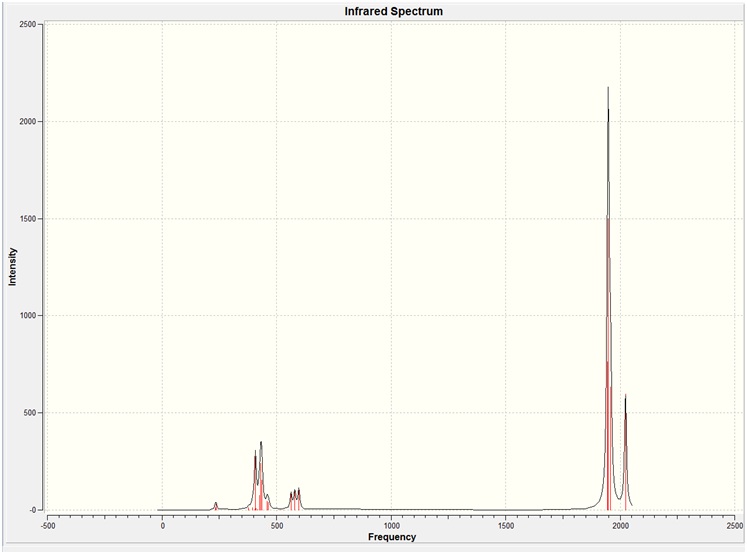
The NH3 molecules that had been optimised previously were used to find the IR spectra for the C3v NH3 molecule, as well as for the d3h molecule. These were compared and contrasted.
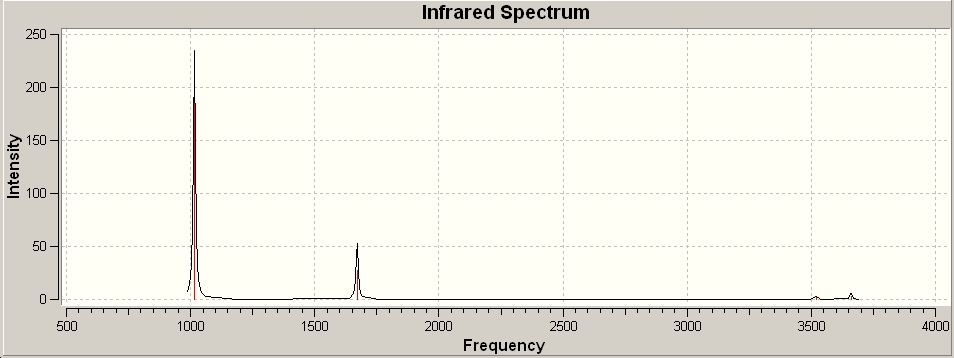
The C3v NH3 yielded the following spectrum:
The same was done for the NH3 with the D3h point group (the transition state). This gave the following IR spectrum:
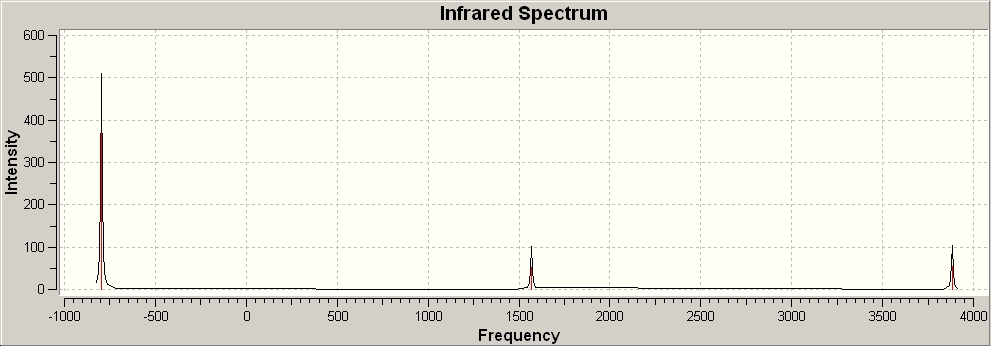
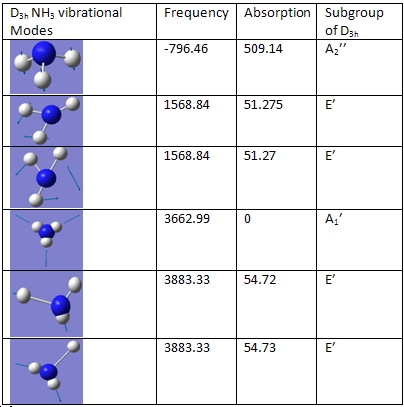
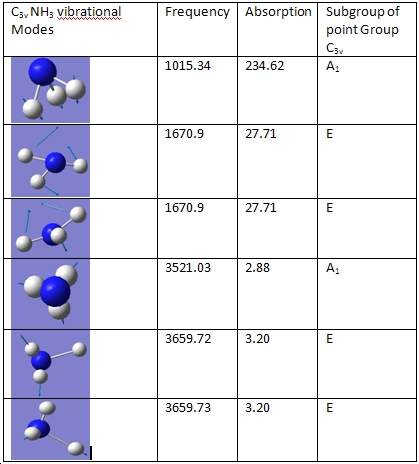
There are 6 vibrational frequencies for both NH3 conformations. However, in the case of the NH3 with D3h symmetry, one of these has a negative frequency, which means that there are 6 positive frequencies for the former conformation and 5 for the latter. From what can be seen from the displacement vectors, the vibrations have the same symmetry elements associated with each other- they vibrate in the same way, except for the first vibrational modes (at 1015 and -796 cm-1 respectively) that have different irriducible representations. The negative vibrational frequency does not actually have any physical meaning- it is merely the result of an algorithm with which this program functions that this particular frequency is rationalised as being negative in character. It is an imaginary vibrational frequency.
These vibrational frequencies compare favourably with those in the literature
The inversion of the molecule is shown in the case of the D3h molecule as the first vibrational mode, where the hydrogen atoms "flap" up and down, while the nitrogen atom remains stationary. This vibration has A2 character. The vibrational mode that corresponds to the inversion reaction in the C3v ammonia molecule is also the first one, where it has A1 symmetry.
Mini Project
The molecule that will be investigated is S2N2, a sulphur nitride that decomposes explosively when struck, or heated above 30oC.1 This molecule is of particular interest, as it polymerises spontaneously at room temperature5. This polymer can conduct electricity in one direction, due to its delocalised nature at room temperature and exhibits superconducting properties at temperatures below the liquid helium temperatures.2,6 This molecule is isoelectronic with both S42+, as well as P2O2. What S2N2 and P2O2 have in common and how they differ will be discussed. This will be done, by examining the bonding, the vibrational frequencies and most importantly, the molecular orbitals, as these will provide the greatest clue as to why the properties of these molecules differ so hugely.
S2N2 decomposes into nitrogen gas and elemental sulphur- the driving force of the reaction of course being the formation of nitrogen gas. This molecule is formed, by passing S4N4 vapour over heated silver wool, pyrex, or glass fibre at 200-300oC.2.The fact that S2N2 polymerises spontaneously to form the polymer shows that the polymerised form is a lot more thermodynamically stable than the monomeric form of the molecule, which shows that the delocalisation of the п orbitals stabilises, as well as the relief of ring strain stabilises the molecule to a huge extent.
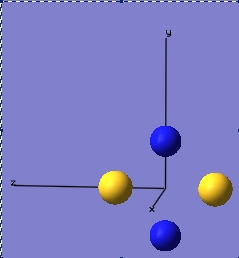
This is the structure of S2N2:
Pentahelicene |
This is actually a delocalised system, which is not visible in ChemDraw. It is widely accepted that there are actually 6 π electrons, rather than 4 as would be implied by the ChemDraw structure. 6X-ray crystallography has shown that this structure is almost square planar in nature.3 Its bond lengths average 1.654Å, which underscores the fact that this is indeed a delocalised structure, as this average bond length coincides almost exactly with average taken from the usual S-N and S=N bonds. 4 According to GaussView, the bond lengths are 1.92Å and have an angle of 87.23o between the bonds. Obviously, Gaussview cannot take the delocalised nature of this molecule into account. What GaussView also got wrong was the point group of the molecule. Experimental data has shown this molecule to have D2h symmetry, whereas GaussView claims that it is actually CS. As all following calculations would be wrong if this geometry is kept, the point group was fixed, so that it would match reality more closely. In this manner, experimental values would successfully be combined with the calculated ones, so that the wheel would not have to be reinvented every time.
With this new optimisation, the point group was indeed D2h, the bond lengths were all 1.81Å and the angles between the atoms were 87.61o. This is still not completely representative of the actual molecule, however part of this excercise is also to see where this model fails and why. Why this model fails is most probably because GaussView does not account for the aromatic nature of this molecule, as it sees it as a collection of fragments that do not interact with each other, whereas this is a molecule with different components that do interact very strongly with one another.
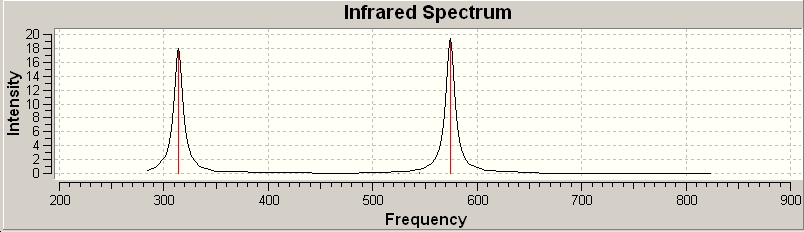
This molecule was then optimised in Gaussview and the IR frequencies were found.
These calculations show that there are only really 2 peaks in the IR; the others have a very low, or negligible absorbance. As it happens, the only IR active vibrations are those with ungerade symmetry, as these are the only ones that induce a change in polarity. This agrees with what has been stated in the literature. However, when comparing these results with those obtained byt the literature, it is found that they are generally lower, implying that the aromaticity of them molecule is not being taken into account6 This is despite the fact that even when the same calculation methods were used as in the literature, the values were still different. The vibrational frequencies also provide a good clue as to how strong the bonds holding the molecule together are.
The fact that the molecule does not optimise to what it ought to be can be explained by the fact that it is stuck in an energy well. Even when the point group and the bond lengths are set and the same basis set is used as in the literature, the optimised structure reverts to a geometry that does not reflect the actual properties of the real molecule. Even when the number of max cycles was increased, the molecule still retained this geometry. Apparently the data from the literature must have overcome this, meaning that they must have had much better processing power and were able to increase the number of cycles even more, so that the next minimum in energy was found.
The bonding of this structure is difficult to account for when only considering valence bond theory, which is why molecular orbital theory has to be used, so as to be able to account for all of the electrons. There are 22 valence electrons in this structure.
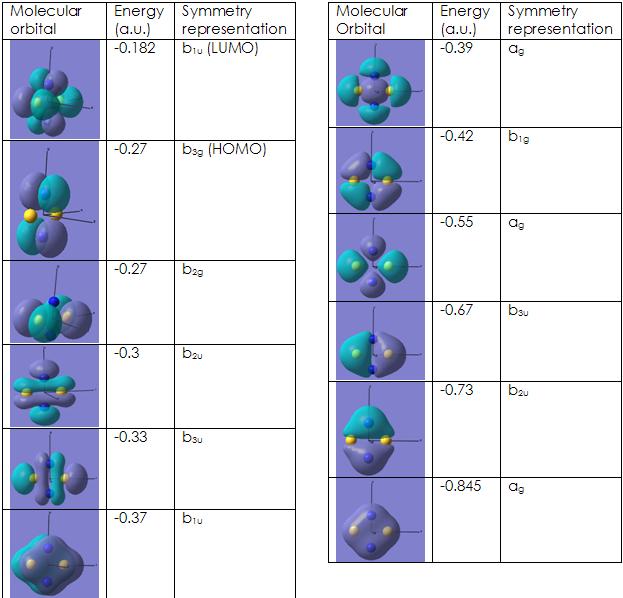
The optimised molecule was then used again to determine the theoretical energies, as well as the structures of the MOs, using the BY3LYP method and the LANL2MB basis set. These structures and their energies are instrumental when finding out just why this molecule is so unstable.
The calculations show that the gap between the HOMO and the LUMO orbitals is not very large. This agrees with what is stated in the literature.6 The molecular orbitals that are of most interest in terms of their contribution to the aromaticity of the molecule are the 3 π orbitals that make this molecule aromatic. These are the HOMO, the HOMO-1 and the HOMO-2. The orbitals that are most interesting in terms of how they contribute to the overall reactivity of the molecule are the LUMO, the LUMO+1 and the LUMO+2, as all three of these molecules are unoccupied, yet are low enough in energy to be able to accomodate electrons. Even though the aromaticity of this molecule has not been fully taken into account, the generation of molecular orbitals ought to be relatively accurate nonetheless.
The visualised molecules were the ones containing the valence electrons and the LUMO (same will apply for the next molecule)
The energies obtained for the MOs are relatively accurate and match literature values quite well. 9
Ideally, S42+ would be analysed to find out how it compares with S2N2, however, Gaussian is not particularly good at optimising molecules that have formal charges, so an uncharged isoelectronic molecule will be used. In this case, this will be P2O2, which will be compared with S2N2
First of all, the square planar optimised structure of P2O2 is going to be optimised and the output of this calculation will be examined. This comparison is valid, as phosphorus is in the same group as nitrogen and oxygen is in the same group as sulphur. The molecule is isoelectronic to S2N2. In the literature, several possible isomers were optimised and compared-some linear7, others cyclised, however as S2N2 is cyclic, it is a cyclised form of the P2O2 that will be compared. It should perhaps be mentioned that this molecule only exists in the realm of the imagination- it has not yet been observed, yet there are papers that have used the same methodology as here to find out what conformation is the most stable.
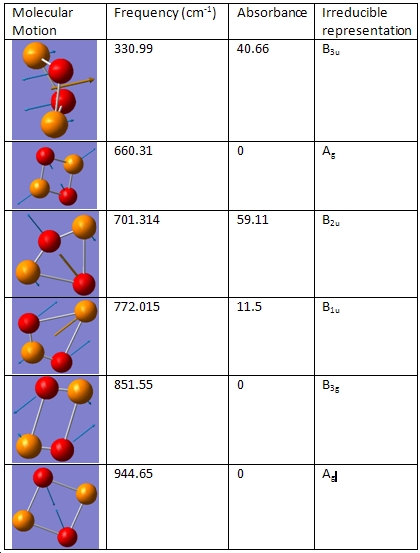
For this optimisation to be successful, the point group symmetry had to be constrained to D2h. The bond lengths were found to be 1.78Å and the bond angles: 80.38o After the initial optimisation, the vibrational frequencies were found.
Pentahelicene |
As with S2N2, the gerade vibrations do not appear on the IR, as they do not induce a change in polarity. This can be seen from the fact that there is no arrow indicating a polar derivative unit vector. When compared with S2N2, it is found that the frequencies are somewhat higher in energy. This can be explained by the fact that phosphorus and oxygen form very strong bonds, as they have better overlap so a higher frequency would be needed to displace this bond. Another difference is that the b1u vibration absorbs a lot more of the incoming radiation than the corresponding vibration in S2N2. There are no negative frequencies, which shows that this molecule is not a transition state- it is at least in theory possible to have this vibration and in theory it ought to be possible to generate this molecule. 8
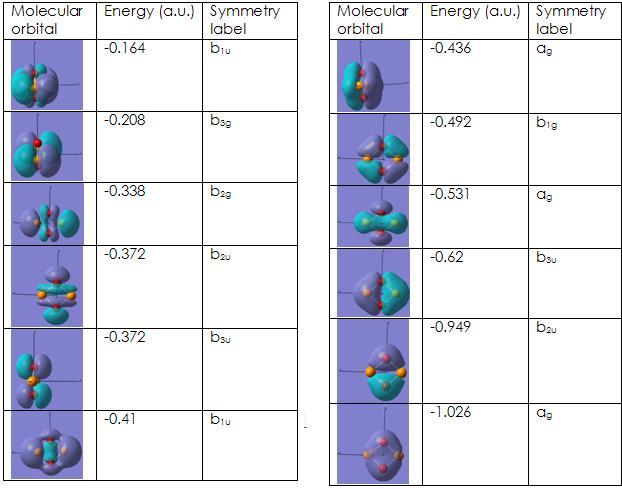
The molecular orbitals were then computed, so as to determine how stable the molecule is. As this molecule is isoelectronic with the previous molecule and also has the same point group, the molecular orbitals ought to look very similar, as only orbitals with the same symmetry can combine. As the difference in electronegativity between the atoms making up the molecules is also similar, the atomic orbitals would have to combine in the same way.
As can be seen, the molecular orbitals do look very similar and they have the same symmetry elements associated with each orbital. From what was found, there was nothing in particular about whether or not P2O2 is aromatic or not, especially seeing as the bond lengths cannot be calculated experimentally. The actual energy of this molecule is given in the calculations as -2187052KJ/mol, which is extremely high in terms of energy.
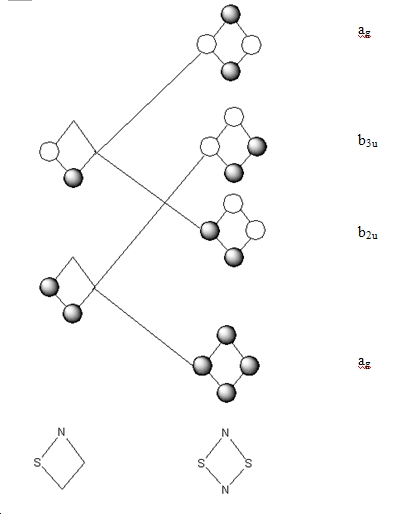
A qualitative MO diagram can be drawn that will be applicable to both molecules, as they have similar polarity disparity, they have the same point group and they are isoelectronic. The MO was generated, by creating fragments and then combining them. The orbitals generated in this way will be compared with the molecular orbitals that were generated by GaussView.
The above qualitative MO diagram for the s orbitals matches perfectly with the calculated version. The p-orbitals, however do not.
When comparing the reactivities of the molecules, S2N2 is most likely to be more reactive, because of the decomposition products. From what can be seen from the IR, P2O2 would have stronger bonds, meaning that it would be less reactive than the former molecule. It is likely that P2 has significant pi contribution to the bonds, yet as this molecule has yet to be made, this will remain unknown. From what is seen in the literature, this molecule has a high biradical character, which would make it very difficult to isolate. This biradical nature cannot be determined by the GaussView calculations, as they do not show this characteristic.
3 D. Scott Warren, Ming Zhao, and Benjamin M. Gimarc, J. Am. Chem. SOC. 195,117, 10345-10352
5 [http://pubs.acs.org/cgi-bin/archive.cgi/inocaj/1976/15/i11/pdf/ic50165a082.pdf C. M. Mikulski, A. G. MacDiarmid, A. F. Garito, and A. J. Heeger,Inorganic Chemistry, Vol. 15, No. 11, 1976]
6 [http://www.sciencedirect.com/science?_ob=ArticleURL&_udi=B6VNG-49NVN1D-3&_user=217827&_rdoc=1&_fmt=&_orig=search&_sort=d&view=c&_version=1&_urlVersion=0&_userid=217827&md5=936c1aa075e04d105380a9caa2fb3a36 Adam J. Bridgeman and Beth Cunningham,Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy Volume 60, Issues 1-2, January 2004, Pages 471-480]
8 [2]