Rep:Mod:cpyx

Introduction

The Gaussian software is a very useful tool in computational chemistry. In the computational physical chemistry lab course, this software was used to optimise the structures of molecules of ammonia, nitrogen, hydrogen as well as the ammonium ion. The bond lengths, bond angles, point groups, final energies and RMS gradient norms of the optimised structures of these species were found. The energies of ammonia, nitrogen and hydrogen were used to determine the reaction energy of the Haber-Bosch process, where ammonia is formed from nitrogen and hydrogen. The vibrations and molecular orbitals of all these species were also analysed using the GaussView software. The atomic charges of ammonia and the ammonium ion were also analysed and compared.

NH₃ molecule

General information

NH3
Calculation	OPTF
Method	B3LYP
Basis Set	6-31G(d,p)
RMS gradient norm (a.u.)	0.00000485
Final energy E (a.u.)	-56.55776873
Point group	C3v
N-H bond length (angstroms)	1.01798
H-N-H bond angle (degrees)	105.741

Optimisation table

Item	Value	Threshold	Converged?
Maximum Force	0.000004	0.000450	YES
RMS Force	0.000004	0.000300	YES
Maximum Displacement	0.000072	0.001800	YES
RMS Displacement	0.000035	0.001200	YES

Predicted change in Energy= -5.986294D-10

The optimisation file is linked to here

Vibrational modes

NH₃ is a non-linear molecule with 4 atoms. Using the 3N-6 rule, I expect to see 3(4)-6 = 6 vibrational modes. The frequencies of these 6 vibrational modes are shown below.

The vibrational modes of NH₃.

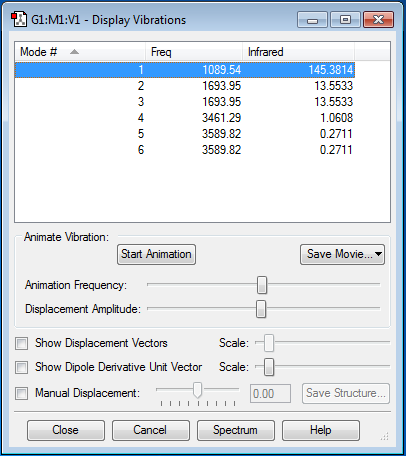
As shown in the table above, some bending and stretching modes have the same frequency, meaning that they have the same energy and are therefore degenerate. Modes 2 and 3 are degenerate, as well as modes 5 and 6.

Modes 1, 2 and 3 are "bending" vibrations whereas modes 4, 5 and 6 are "bond stretch" vibrations. It can be seen from the table above that "bending" vibrations have much lower frequencies as compared to "bond stretch" vibrations.

Mode 4, which is the symmetric stretching of all the N-H bonds, is a highly symmetric mode. Mode 1 is the bending of all the N-H bonds in a similar direction, such that all the bonds bend inwards together or all the bonds bend outwards together. It is known as the "umbrella" mode as the bending is very similar to the way that an umbrella is opened up and closed. As all the N-H bonds bend in a similar direction in mode 1, there is a large change in dipole moment of the molecule, resulting in a high IR intensity of 145.3814.

Although there are 4 distinct vibrational modes, I would only expect to see 2 bands in an experimental IR spectrum of gaseous ammonia. These correspond to mode 1 and degenerate modes 2 and 3. As shown in the right column in the table above, the IR intensities of modes 4, 5 and 6, which are all "bond stretch" vibrations, are very low as compared to the IR intensities of modes 1,2 and 3, which are all "bending" vibrations. The reason for the low IR intensities of the "bond stretch" vibrations as compared to the "bending" vibrations in NH₃ is that "bond stretch" vibrations cause a very small change in dipole moment of this particular molecule, much smaller than the change in dipole moment caused by "bending" vibrations. Therefore, the intensities of the peaks in the IR spectrum corresponding to modes 4,5 and 6 are too low to be seen.

Atomic charges

Atom	Charge
Nitrogen	-1.125
Hydrogen	+0.375

NH₃ is a neutral molecule with covalent bonding between the central nitrogen atom and the hydrogen atoms. As nitrogen is a more electronegative element as compared to hydrogen, the shared electrons in each of the 3 N-H bonds in the molecule will be pulled closer to the central nitrogen atom. These N-H bonds are polar covalent bonds. Thus, I expect the nitrogen atom to take on a negative charge and the 3 hydrogen atoms to all take on the same positive charge, which is really the case as shown in the table above. Adding up all the charges of the nitrogen atom and the 3 hydrogen atoms shown above gives 0, which shows that NH₃ is indeed a neutral molecule.

N₂ molecule

General information

N2
Calculation	OPTF
Method	B3LYP
Basis Set	6-31G(d,p)
RMS gradient norm (a.u.)	0.00000060
Final energy E (a.u.)	-109.52412868
Point group	D∞h
N-N bond length (angstroms)	1.10550

Optimisation table

Item	Value	Threshold	Converged?
Maximum Force	0.000001	0.000450	YES
RMS Force	0.000001	0.000300	YES
Maximum Displacement	0.000000	0.001800	YES
RMS Displacement	0.000000	0.001200	YES

Predicted change in Energy= -3.401087D-13

The optimisation file is linked to here

Display vibrations

Frequency	Infrared
2457.33	0.0000

Only 1 vibrational mode is shown, which is the stretching of the N-N triple bond. As a molecule of N₂ contains only 2 identical nitrogen atoms, it does not have a dipole moment. Therefore, this "bond stretch" vibration does not cause a change in dipole moment and is not detected in IR spectroscopy, resulting in an IR intensity of 0.

Molecular orbitals

When 2 atoms form a molecule, the molecular orbitals (MO) are constructed from atomic orbitals by linear combination. The total number of electrons in the MO diagram is the total number of electrons in the whole molecule. A nitrogen atom contains 7 electrons and has an electronic configuration of 1s²2s²2p³, so the diatomic N₂ molecule has a total of 14 electrons. The covalent bond between the 2 nitrogen atoms in this molecule is a triple bond, so all the 3 electrons in the 2p orbitals in each nitrogen atom are involved in bonding. The 2p electrons form 1 sigma and 2 pi bonds. There is stabilisation in this bonding as the corresponding antibonding orbitals of these bonding orbitals are empty and do not contain electrons. Bonding orbitals have a lower energy while antibonding orbitals have a higher energy than the corresponding atomic orbitals.

Although all the 14 electrons in the N₂ molecule are involved in bonding, the stabilisation achieved by the filling of the 1s and 2s sigma bonding orbitals is cancelled out by the destabilisation caused by the filling of the corresponding antibonding orbitals. This means that the stabilisation of the N₂ molecule as compared to the individual nitrogen atoms is due to bonding between the electrons in all the 2p orbitals in the molecule.

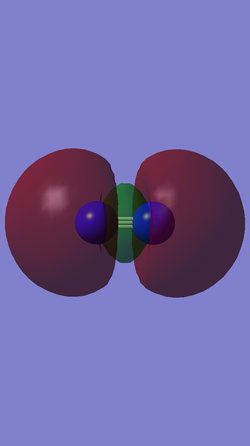
When a molecule donates electrons to another substance, the electrons from the highest occupied molecular orbital (HOMO) are removed so as to remove the most energy from the molecule. Electrons that are donated to the molecule will be placed in the unoccupied molecular orbital with the lowest energy level, known as the lowest unoccupied molecular orbital (LUMO). The table below shows representations of the HOMO and LUMO of N₂.

HOMO	LUMO

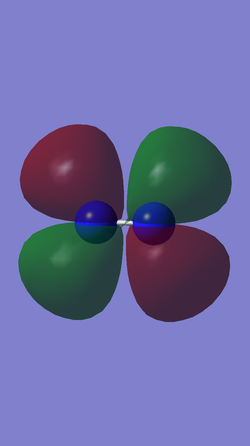
H₂ molecule

General information

H2
Calculation	OPTF
Method	B3LYP
Basis Set	6-31G(d,p)
RMS gradient norm (a.u.)	0.00005270
Final energy E (a.u.)	-1.17853935
Point group	D∞h
H-H bond length (angstroms)	0.74292

Optimisation table

Item	Value	Threshold	Converged?
Maximum Force	0.000091	0.000450	YES
RMS Force	0.000091	0.000300	YES
Maximum Displacement	0.000120	0.001800	YES
RMS Displacement	0.000170	0.001200	YES

Predicted change in Energy= -1.063105D-08

The optimisation file is linked to here

Display vibrations

Frequency	Infrared
4463.86	0.0000

Like N₂, there is only 1 vibrational mode in H₂. In this case, the vibrational mode is the stretching of the H-H bond. As a molecule of H₂ contains only 2 identical hydrogen atoms, it does not have a dipole moment. Therefore, this "bond stretch" vibration does not cause a change in dipole moment and is not detected in IR spectroscopy, resulting in an IR intensity of 0.

The frequency of the "bond stretch" vibration in H₂ is much higher than the frequency of the "bond stretch" vibration in N₂ as the reduced mass of H₂ is smaller than the reduced mass of N₂. Reduced mass is inversely proportional to vibrational frequency.

Molecular orbitals

The table below shows representations of the HOMO and LUMO for the H₂ molecule. An atom of hydrogen contains 1 electron and hydrogen has an electronic configuration of 1s¹. Thus, there are only 2 electrons in a molecule of H₂, and both electrons are involved in sigma bond formation between the 2 hydrogen atoms in the molecule. The HOMO is the sigma bonding orbital and the LUMO is the sigma* antibonding orbital.

HOMO	LUMO

The Haber-Bosch process

The chemical equation for this process is:

N₂ + 3H₂ $\to$ 2NH₃

All data recorded in the table below is in au.

E(NH3)	-56.55776873
2*E(NH3)	-113.11553746
E(N2)	-109.52412868
E(H2)	-1.17853935
3*E(H2)	-3.53561805
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]	-0.05579073

ΔE = -0.05579073 x 2625.5 = -146.478561615 kJ/mol

ΔE is negative, indicating that energy is released from the system to the surroundings when ammonia is formed from the gaseous reactants of nitrogen and hydrogen. This means that the ammonia product is lower in energy and more thermodynamically stable than the reactants. The forward reaction producing ammonia is favoured.

NH₄⁺ ion

General information

NH4+
Calculation	OPTF
Method	B3LYP
Basis Set	6-31G(d,p)
RMS gradient norm (a.u.)	0.00011991
Final energy E (a.u.)	-56.90586436
Point group	Td
N-H bond length (angstroms)	1.02761
H-N-H bond angle (degrees)	109.471

Comparison of H-N-H bond angle between NH₃ and NH₄⁺

The difference between NH₄⁺ and NH₃ is that NH₄⁺ contains 1 more proton. NH₃ and NH₄⁺ are conjugate acid-base pairs, with NH₄⁺ being the conjugate acid and NH₃ being the conjugate base.

Both NH₃ and NH₄⁺ have tetrahedral pseudostructures. NH₄⁺ contains 4 bond pairs and no lone pairs of electrons around the central nitrogen atom. On the other hand, NH₃ contains 3 bond pairs and 1 lone pair of electrons around the central nitrogen atom. Thus, NH₄⁺ has a tetrahedral structure whereas NH₃ has a trigonal pyramidal structure.

According to the Valence Shell Electron Pair Repulsion (VSEPR) theory, lone pair-lone pair repulsions are considered to be stronger than lone pair-bond pair repulsions and lone pair-bond-pair repulsions are considered to be stronger than bond pair-bond pair repulsions. There are no lone pair-lone pair repulsions within a NH₃ molecule and within a NH₄⁺ ion. However, there are lone pair-bond pair repulsions within a molecule of NH₃ due to the lone pair of electrons on the central nitrogen atom and the 3 electron pairs in the 3 N-H bonds. NH₄⁺ does not have any lone pair of electrons on the central nitrogen atom, so there are no lone pair-bond pair repulsions exhibited in NH₄⁺. This results in the H-N-H bond angle in NH₃ being smaller than the H-N-H bond angle in NH₄⁺.

The H-N-H bond angles found by optimisation of the structures of NH₃ and NH₄⁺ are 105.741 degrees and 109.471 degrees respectively. Clearly, the H-N-H bond angle in NH₃ is found to be smaller than the H-N-H bond angle in NH₄⁺. Therefore, these bond angles found are consistent with the VSEPR theory.

Optimisation table

Item	Value	Threshold	Converged?
Maximum Force	0.000232	0.000450	YES
RMS Force	0.000124	0.000300	YES
Maximum Displacement	0.000538	0.001800	YES
RMS Displacement	0.000288	0.001200	YES

Predicted change in Energy= 2.801952D-07

The optimisation file is linked to here

Vibrational modes

NH₄⁺ is a non-linear molecule with 5 atoms. Using the 3N-6 rule, I expect to see 3(5)-6 = 9 vibrational modes. The frequencies of these 9 vibrational modes are shown below.

The vibrational modes of NH₄⁺.

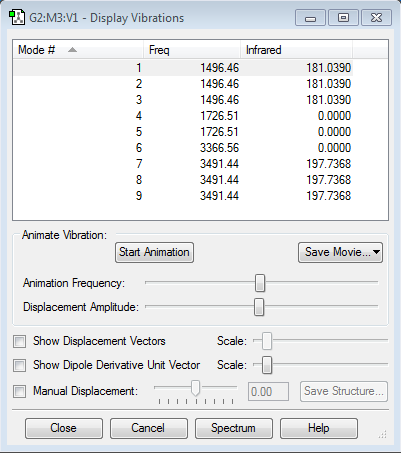
As shown in the table above, some bending and stretching modes have the same frequency, meaning that they have the same energy and are therefore degenerate. Modes 1, 2 and 3 are degenerate, as well as modes 4 and 5. Modes 7, 8 and 9 are also degenerate.

Modes 1, 2, 3, 4 and 5 are "bending" vibrations whereas modes 6, 7 and 8 and 9 are "bond stretch" vibrations. As with ammonia, it can be seen from the table above that "bending" vibrations have much lower frequencies as compared to "bond stretch" vibrations.

Mode 6 is the symmetric stretching of all the N-H bonds. This "bond stretch" vibration does not cause a net change in dipole moment of the tetrahedral ammonium ion, hence it is not detected in IR spectroscopy, resulting in an IR intensity of 0.

However, modes 7, 8 and 9 are assymetric stretches of all the N-H bonds. They cause a net change in dipole moment of the ammonium ion, such that it is larger than the change in dipole moment caused by all the "bending" vibrations. This results in modes 7, 8 and 9 having the greatest IR intensities of 197.7368.

Atomic charges

Atom	Charge
Nitrogen	-0.999
Hydrogen	+0.500

Just as in ammonia, there is covalent bonding in the ammonium ion NH₄⁺ between the central nitrogen atom and the hydrogen atoms. As the nitrogen atom is more electronegative than the hydrogen atoms, it pulls the shared electrons in each of the 4 N-H bonds in the ion closer to itself. These N-H bonds are polar covalent bonds. Thus, I expect the nitrogen atom to take on a negative charge and the 4 hydrogen atoms to all take on the same positive charge, which is really the case as shown in the table above. Adding up all the charges of the nitrogen atom and the 4 hydrogen atoms shown above gives 1.001, which shows that the charge of the ammonium ion is indeed +1.

Comparison of atomic charges between NH₃ and NH₄⁺

Atom	Charge in NH3	Charge in NH4+
Nitrogen	-1.125	-0.999
Hydrogen	+0.375	+0.500

The magnitude of the negative charge on the nitrogen atom is much lower in NH₄⁺ than in NH₃. This is because in NH₄⁺, a pair of electrons is donated from the central nitrogen atom to a hydrogen atom to form a dative bond. However, NH₃ has a lone pair of electrons on the central nitrogen atom. Thus, there is a higher electron density around the nitrogen atom in NH₃ than around the nitrogen atom in NH₄⁺, so the nitrogen atom in NH₃ carries a greater negative charge.

However, the hydrogen atoms in NH₄⁺ carry a greater positive charge than the hydrogen atoms in NH₃. This is because the electrons in the N-H bonds can be pulled closer to the central nitrogen atom in NH₄⁺ as there is no lone pair-bond pair electronic repulsion in NH₄⁺ when there is lone pair-bond pair electronic repulsion in NH₃. Thus, there is a lower electron density around the hydrogen atoms in NH₄⁺ than in NH₃, so the hydrogen atoms in NH₄⁺ carry a greater positive charge.

Molecular orbitals

The molecular orbitals of the ammonium ion were visualised using the GaussView software. Images of 5 of these visualised molecular orbitals were captured and saved as files. They are shown below.

MO 12 This is a high energy unoccupied antibonding MO with an energy of 0.33259 au. This is a positive value, showing that the MO is quite high in energy. A higher p orbital of the nitrogen atom and s orbitals on the hydrogen atoms contribute to this MO. However, the contribution from the s orbitals of the hydrogen atoms is much smaller than the contribution from the particular p orbital of the nitrogen atom. There is unfavourable interaction between a lobe of the p orbital and the s orbitals of the 2 adjacent hydrogen atoms which are both in a different phase from the lobe of the p orbital. This results in the antibonding character of this MO. This MO is similar in structure and has exactly the same energy as 2 other unoccupied antibonding orbitals, which are MO 10 and MO 11. These 3 orbitals are different mainly in terms of their spatial orientation.
MO 9 This is a high energy unoccupied antibonding MO with a slightly high energy of -0.12843 au. A 2p orbital of the nitrogen atom and the 1s orbitals on the hydrogen atoms contribute to this MO, so this is the antibonding combination of the HOMO. The contribution from the 1s orbitals of the hydrogen atoms is larger than the contribution from the 2p orbital of the nitrogen atom. There is unfavourable interaction between a lobe of the 2p orbital and the 1s orbitals of the 2 adjacent hydrogen atoms which are both in a different phase from the lobe of the 2p orbital. This results in the antibonding character of this MO. This MO is similar in structure and has exactly the same energy as 2 other unoccupied antibonding orbitals, which are MO 7 and MO 8. Like the degenerate orbitals of MO 3, MO 4 and MO 5, these 3 orbitals are different mainly in terms of their spatial orientation.
MO 6 This is the LUMO or lowest unoccupied molecular orbital of the ammonium ion with an energy of -0.21003 au. It has a spherical shape, similar to the very low energy filled orbitals. The 2s orbital of nitrogen and the 1s orbitals of the hydrogen atoms contribute to the electron density of this MO. The MO has antibonding character due to the nitrogen atom being in a different phase from all the hydrogen atoms. This is the antibonding combination of MO 2.
MO 5 This is a bonding HOMO or highest occupied molecular orbital of the ammonium ion with an energy of -0.82471 au. A 2p orbital of the nitrogen atom and the 1s orbitals on the hydrogen atoms contribute to this MO. There is favourable interaction between a lobe of the p orbital and the 1s orbitals of the 2 adjacent hydrogen atoms which are in the same phase as the lobe of the p orbital. This results in the bonding character of this MO. This MO is similar in structure and has exactly the same energy as 2 other filled bonding orbitals, which are MO 3 and MO 4. These 3 orbitals are different mainly in terms of their spatial orientation. All the 3 orbitals can be considered HOMOs.
MO 2 This is a filled bonding orbital with a very low energy of -1.24808 au. The 2s orbital of nitrogen and the 1s orbitals of the hydrogen atoms contribute to the electron density of this MO. All the atoms are in the same phase, resulting in the deep bonding character of this MO.