Rep:Mod:cpc112

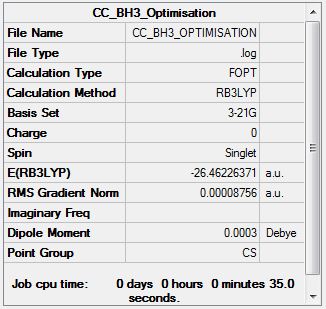
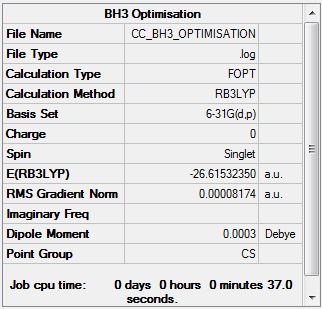
Borane (B3LYP/3-21G)

Optimisation log file here

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000217 0.000450 YES RMS Force 0.000105 0.000300 YES Maximum Displacement 0.000919 0.001800 YES RMS Displacement 0.000441 0.001200 YES Predicted change in Energy=-1.635270D-07 Optimization completed.	Optimised Borane Molecule

Borane - Improved Basis Set (B3LYP/6.21G(d,p))

Optimisation log file here

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000203 0.000450 YES RMS Force 0.000098 0.000300 YES Maximum Displacement 0.000849 0.001800 YES RMS Displacement 0.000415 0.001200 YES Predicted change in Energy=-1.436187D-07 Optimization completed.	Optimised Borane Molecule

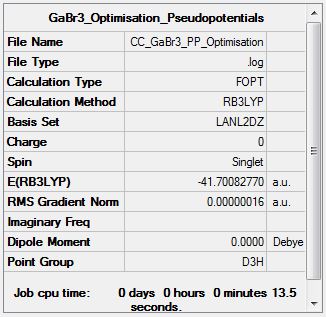
GaBr₃

Optimisation log file DOI:10042/143670

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000003 0.001800 YES RMS Displacement 0.000002 0.001200 YES Predicted change in Energy=-1.307761D-12 Optimization completed.	Optimised Gallium Bromide Molecule

BBr₃

Optimisation log file DOI:10042/143677

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000011 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.000047 0.001800 YES RMS Displacement 0.000031 0.001200 YES Predicted change in Energy=-6.849813D-10 Optimization completed.	Optimised Boron Bromide Molecule

Optimisation log file DOI:10042/143669

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000036 0.001800 YES RMS Displacement 0.000024 0.001200 YES Predicted change in Energy=-4.086282D-10 Optimization completed.	Optimised Boron Bromide Molecule

Geometry Comparison

It is important to note that the values reported for Borane in the following table were obtained via calculations using the improved 6.21G (d,p) basis set.

Geometry Data

Parameter	BH3	GaBr3	BBr3
r(E-X) (Å)	1.19	2.35	1.93
θ(X-E-X) (º)	120	120	120

---

Structural Comparison

The compounds which have been presented above are all of the form EX₃, adopt a trigonal planar (D₃H) structure (consistent bond angle of 120°) and are electron deficient species. This electron deficiency is of vital importance in understanding the chemical and bonding characteristics of these species, in partricular their Lewis acidity. In a purely covalent model, in which contributions from ionic and other sources are assumed negligible, the predicted covalent bond lengths from the literature would be as follows; B-H (115pm), B-Br (204pm), Ga-Br (238pm) ^[1]. This is clearly a crude analysis, however, it is logical that as we progress from BH₃ to BBr₃ to GaBr₃ that the bond length would increase, as predicted by the covalent bond lengths calculated by analysis of the covalent radii of the constituent atoms. The predicted B-H covalent bond length (115pm) appears to be relatively accurate in comparison to the calculated bond length (119pm), with the deviation being accounted for by the combined error range of prediction and calculation, indicating that the bonding in this structure is accurately described by a purely covalent bonding model. It is worthy of note that under standard conditions BH₃ would in fact exist in dimeric form, the bonding characteristics of which are much more complex due to the existence of 3c-2e bridging bonds. The predicted B-Br bond length (204pm) compares less favourably to the calculated bond length (1.93pm) and therefore the deviation cannot be accounted for entirely by the combined error range of prediction and calculation. The deviation from the predicted bond length could be a result of π-stabilisation facilitated by the electron deficiency (Lewis Acidity) of the Boron centre, accepting electron density from the lone pairs of the Bromine substituents. This is not a formal electron donation as may be observed in adducts of Lewis Acids and Lewis Bases, however, Bromine is able to donate electron density from its lone pairs into the vacant sp² hybridised orbital of the Boron centre, increasing the bond order of the B-Br bond which explains the decreased bond length in comparison to purely covalent predictions. The predicted Ga-Br covalent bond length (238pm) again appears to be relatively accurate in comparison to the calculated bond length (235pm), with the deviation being accounted for by the combined error range of prediction and calculation, indicating that the bonding in this structure is accurately described by a purely covalent bonding model as in the B-H example. The Gallium centre has a much larger covalent radius than Boron and therefore the Ga-Br bond length (235pm) is much larger than the B-Br bond length (193pm) and the combination of the decreasing strength of π-bonding with bond length in addition to the decreased overlap of the mismatched orbitals results in a much lower degree of π-stabilisation. The Gallium centre has a lower degree of electron deficiency (Lewis Acidity) and π-stabilisation, therefore the bonding can be accurately described by a purely covalent bonding model as previously stated.

Definition of a Bond

The concept of a chemical bond is one which is hard to define, therefore for the majority of this analysis we will restrict ourselves to the discussion of covalent bonding systems which are most relevant to the examples above. Simplistically, a bond can be seen as merely interaction between two nuclei such that they retain an essentially constant internuclear separation. The Born-Oppenheimer approximation postulates that the energy of of a system is independent of nuclear motion, therefore the Hamiltonian operator does not contain a term relating to the kinetic energy of the nuclei - their positions are assumed fixed. This is merely a simplification and of course does have its limitations, however the primary implication of this approximation is that the electron density instantaneously adapts to any nuclear motion or oscillation. In the vast majority of cases species are represented in the most stable state such that the bonds (represented simply as lines) are at their equilibrium distance and potential energy is minimised. The constituent atoms both contribute electron density which resides primarily between the two positively charged nuclei acting to bring the nuclei to the optimal internuclear distance and hence forming a bond. Therefore, it could be postulated that a chemical bond is merely a region of high electron density, however, it must then be considered that high electron density may also be a result of non-bonding lone pairs outside the internuclear region yielding the following definition of a chemical bond; a region of high electron density between two or more nuclei. As mentioned previously, this applies solely to covalent bonding, without reference or consideration of the effects of ionic or metallic bonding which arise from different phenomena than covalent bonding. In these examples, a definition could be attained by analysis of the electrostatic interactions of ions.

In a broader sense, via application of Molecular Orbital theory, the definition above still applies to a certain degree although there are a few more important factors which are discussed below such that our definition can be applied to all categories of bonding (ionic, covalent, metallic). Firstly, it must be noted that few Molecular Orbitals can be seen to exhibit purely bonding characteristics i.e. there are often both in-phase (bonding) interactions and out-of-phase (ant-bonding) interactions present in a Molecular Orbital. Therefore, the overall bonding character of the Molecular Orbital can only be deciphered by comparison of the relative intensity of the bonding and anti-bonding interactions. In addition, Molecular Orbitals with the greatest symmetry demonstrate an increased degree of bonding character. Despite these extra pieces of information, the Molecular Orbital definition of a bond is still comparatively vague and in order to improve this we must consider the differences between primary and secondary orbital overlap. Primary orbital interaction results in the formation of Natural Bonding orbitals whereas secondary orbital interactions simply indicate stereo-electronic interactions, therefore in defining a bond primary orbital interactions are of primary importance. Therefore, in terms of Molecular Orbital theory a bond can be defined as a region between two nuclei in which Molecular Orbitals with overall bonding character, as defined above, have greater occupation than anti-bonding Molecular Orbitals.

Strength of Bonding Interactions

The strength of bonding interactions is difficult to define due to there being large differences between, for example, the broad categories of ionic and covalent bonding. As mentioned previously these categories of bonding interaction arise from different phenomena, resulting in ionic bonding generally being stronger than covalent bonding, whereas intermolecular hydrogen-bonding interactions are extremely weak even in comparison to covalent bonding interactions. Despite this, it is important to note that few bonds could be defined as either purely covalent or ionic - the bonding characteristics of molecules is a sliding scale such that bonds usually possess some degree of both ionic and covalent character (they are polarised).

Ionic bonding is dependent on the coulombic interaction of oppositely charged ions and is often reported in the form of lattice energies. Ionic bonding is in general the strongest form of bonding interaction, for example, the Li-F bond strength is 1036 kJmol^{-1 [9]}. Even for ionic bonding, this is particularly strong due to the contracted nature of the Li and F orbitals which therefore interact strongly.

At the opposite end of the spectrum is hydrogen bonding which is a very weak interaction, however, it still comes under the umbrella of bonding. Obviously, even within hydrogen there is variation in the strength of interaction - a typical example is water in which the strength of hydrogen bonding interactions is 23.3 kJmol^{-1 [10]}.

For the remainder of this analysis we will again restrict ourselves to consideration of the covalent bonding systems which are most relevant to the previous examples. Within this analysis covalent bonding would be defined as a medium strength interactions, however, even within the region of covalent bonding there is potentially large variations in the strength of bonding interactions. For example, diatomic Nitrogen possesses an extremely strong N-N triple bond (941 KJ^-1) ^[9] within which there is very high electron density in the internuclear region, whereas diatomic halogen species exhibit very weak covalent X-X bonding interactions (F-F: 158 kJmol^-1) ^[9] due to repulsive interactions of the halogen lone pairs in close proximity. The strength of covalent bonding is significantly affected by the efficiency of orbital overlap, which decreases as orbitals become more diffuse down a group, and the difference in electronegativity of the constituent atoms, introducing polarisation to the bond. Even relatively weak covalent bonding interactions such as diatomic Fluorine described above are much stronger than electron-deficient bonding interactions such as the 3c-2e bridging bonds in di-borane.

Gaussian Bonding Interpretation

Gaussian operates a crude definition of bonding in which internuclear separations are compared to pre-determined values which are assumed to constitute a bonding interaction, therefore particularly weak bonding interactions are often not recognised by the software. An example of the limitations of this crude definition is that the B-H (2c-2e) bond in BH₃ and the B-H-B (3c-2e) bond present in B₂H₆ are both assumed to fall within the definition of a simple B-H single bond, however, this is clearly not the case despite bonding interactions being present in both species. Therefore it is likely that low-level Gaussian calculations would fail to optimise the structure of B₂H₆ entirely or recognise the existence of a bonding interaction, resulting in the B-H-B (3c-2e) bond not being represented in the optimised structure. In terms of optimising structures and predicting properties Gaussian is extremely useful, however, the output data still requires interpretation to achieve the desired results.

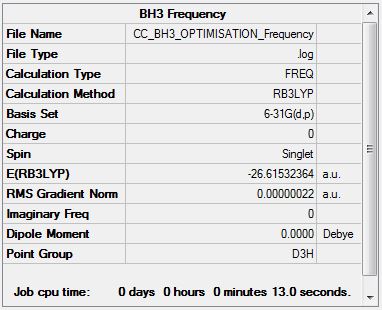
Borane Frequency Analysis

Frequency log file here

Summary Data	Low Modes
	Low frequencies --- -9.6311 -9.6170 -0.1740 0.0005 0.5207 1.0594 Low frequencies --- 1162.9886 1213.1485 1213.1487

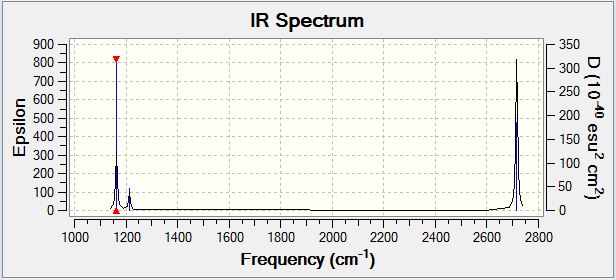
Borane Vibrational Spectrum

Wavenumber	Intensity	IR active	Type
1163	93	Yes	Bend (Wag)
1213	14	Yes (Very Slight)	Bend (Scissoring and Rocking)
1213	14	Yes (Very slight)	Bend (Scissoring)
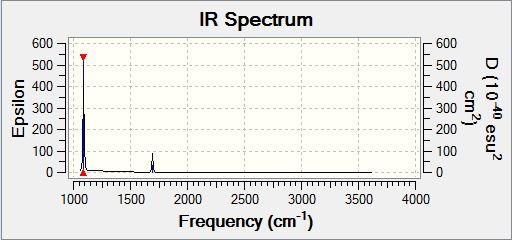
2583	0	No	Stretch (Symmetric)
2716	126	Yes	Stretch (Anti-symmetric)
2716	126	Yes	Stretch (Anti-symmetric)

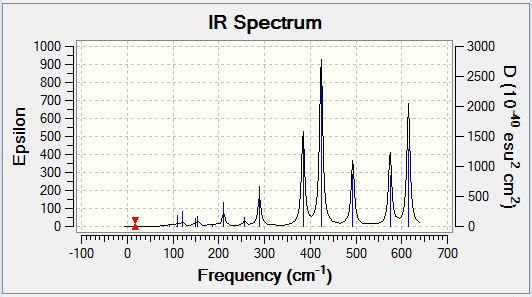
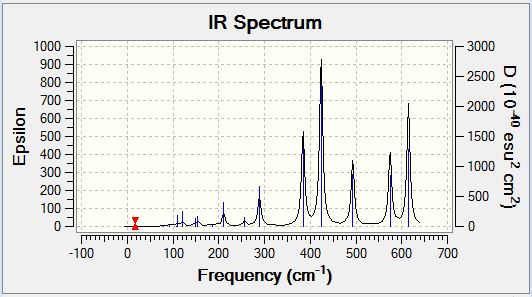
BH₃ has 3N-6 potential vibrational modes yielding six potential IR active vibrational modes, however, the selection rule for IR spectroscopy is that there must be a variation in the molecular dipole moment upon vibrational excitation. The intensity of the observed peaks is proportional to the magnitude of the variation in molecular dipole moment. Analysis of the spectrum above indicates that the anti-symmetric stretching modes cause the greatest variation in molecular dipole moment, whereas the degenerate rocking and scissoring modes cause the lowest variation in molecular dipole moment. The symmetric stretch (2583cm^-1) is not an IR active vibrational mode and hence does appear in the IR spectrum, however, it could potentially be visualised by the application of Raman Spectroscopy. The selection rule described above is responsible for the observation of only five peaks in the IR spectrum of BH₃ despite there being six potential vibrational modes as the five which are observed all cause a variation in the molecular dipole moment, whereas the IR inactive mode which is not observed does not.

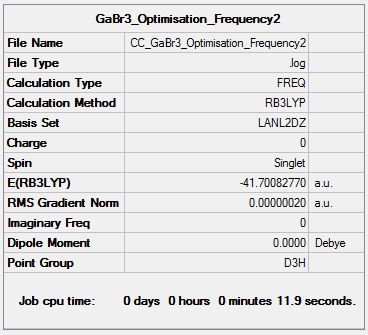
GaBr₃ Frequency Analysis

Frequency log file DOI:10042/146989

Summary Data	Low Modes
	Low frequencies --- -1.4878 -0.0015 -0.0002 0.0096 0.6540 0.6540 Low frequencies --- 76.3920 76.3924 99.6767

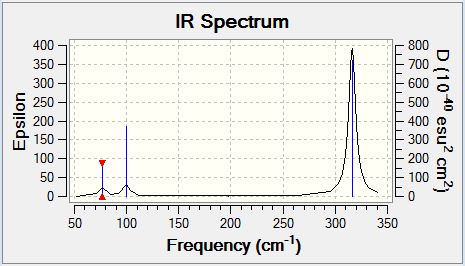
GaBr₃ Vibrational Spectrum

Wavenumber	Intensity	IR active	Type
76	3	Yes	Bend
76	3	Yes (Slight)	Bend
100	9	Yes (Slight)	Bend
197	0	No	Stretch (Symmetric)
316	57	Yes	Stretch
316	57	Yes	Stretch

Comparison of the Vibrational Spectra of BH₃ and GaBr₃

It would be expected that the vibrational spectra of both BH₃ and GaBr₃ would exhibit a total of six vibrational modes as predicted by the 3N-6 rule (N refers to the number of constituent atoms). This is due to their identical non-linear trigonal planar structure with a group 13 centre and results in the observation an equal number of peaks in the vibrational spectra. The frequency analysis confirms the existence of six potential vibrational modes, however, there are in fact only three peaks clearly visible on the vibrational spectrum of each. Both molecules exhibit only three peaks due to the existence of two degenerate vibrational modes and one peak of zero intensity as a result of the IR selection rule discussed previously.

Despite the clear similarities in the vibrational spectra of the two trigonal planar species, there is also a significant contrast between the two. The most obvious difference is the comparative energies of the vibrational modes observed with the BH₃ vibrations being higher in energy than their GaBr₃ equivalents. It is not possible to compare the total molecular energies of the respective molecules in this analysis as the data was obtained using different basis set calculations. Furthermore, the intensity of the peaks observed in the vibrational spectrum of BH₃ are large in comparison to those of GaBr₃, indicating that the vibrational modes of BH₃ result in a larger variation in the molecular dipole moment (as explained below). The final difference in the spectra is the degeneracy of vibrational modes - in BH₃ the second lowest energy (scissoring and rocking) modes and the highest energy (anti-symmetric stretch) modes are degenerate whereas in GaBr₃ the lowest energy (bending) modes and the highest energy (stretching) modes are degenerate.

Implications of the variation in Frequencies for BH₃ and GaBr₃

Classically the vibrational frequency is proportional to the force constant and reduced mass as follows: v = (1/2π)k/μ. The force constant (k) in this equation is the second derivative of the potential energy and is therefore proportional to the strength of the bond in question. It might be expected that GaBr₃ may in fact have a larger force constant as the Ga-Br bond would exhibit a degree of π-character not present in BH₃. This potential π-interaction is due to the donation of the lone pair electron density on Bromine to the empty p-orbital of Gallium which is not possible in BH₃ where the bonding is purely sigma in character. However, in truth the increased orbital overlap in BH₃, due to the better size match of Boron and Hydrogen in comparison to that of Gallium and Bromine, results in a stronger force constant for this B-H bond. Therefore the B-H bond length is lower than that of Ga-Br and the vibrational modes are of higher energy as would be predicted by application of the equation stated previously.

Comparison of the relative frequency and intensity of the Umbrella motion in BH₃ and GaBr₃

Analysis of the Umbrella motion in both BH₃ and GaBr₃ quickly yields the conclusion that the vibrational frequency of this mode is much larger in BH₃ (1163 cm^-1) than GaBr₃ (100 cm^-1) and the intensity of the vibrational mode is much greater in BH₃. The observation above can be explained by the greater reduced mass of GaBr₃ and the increased bond strength in BH₃, both of which reduce the vibrational frequency of GaBr₃ as predicted by the equation stated previously (above). In addition the intensity of the peak is reduced in GaBr₃ as a result of the reduced variation in dipole moment in comparison to BH₃. The reduced variation in dipole moment can be explained by comparatively large displacement of the Gallium atom in comparison to Bromine whereas in BH₃ the Umbrella mode is dominated by the motion of Hydrogen. The large magnitude of the motion of Hydrogen relative to the Boron centre in BH₃ is responsible for the increased variation in dipole moment. In general it can be concluded that more massive atoms demonstrate much lower displacement during vibrational modes.

Reasoning for the application of the same methodology and basis set in Optimisation and Frequency Analysis

The vibrational frequencies of a molecule can be obtained by taking the second derivative of the nuclear coordinates in cartesian space, however, such an analysis is only valid if the molecule has been optimised such that the gradient in the potential energy surface is equal to zero. In addition, the gradient on the potential energy surface can be zero at the transition state as well as at the desired optimised structure. The effect of varying the basis set during the analysis can be stark, for example, causing the point group of the molecule to change. This is due to the basis set not allowing the calculation to proceed with enough accuracy to identify the truely optimised structure, therefore, the optimised energy displays a significant degree of error. Application of a different basis set in the frequency analysis would introduce a further layer of error such that the energy values are no longer comparable and this is the reason why the methodology and basis set must be kept constant in order for results to be reasonably compared.

Purpose of Frequency Analysis

In the simplest possible terms, the purpose of frequency analysis is to determine whether the structure obtained during optimisation actually corresponds to an optimised structure or alternatively to a transition state. This is necessary due to the methodology of optimisation utilised by Gaussian such that points of zero gradient on the potential energy surface are identified without consideration of whether they correspond to a zero-point energy or alternative points of zero gradient such as transition states. Frequency analysis therefore probes the second derivative of the potential energy surface to determine whether the optimised structure corresponds to either an energy maxima (transition state) or an energy minima (optimised structure). If any of the low frequencies obtained are stated to be negative then it can be concluded that the structure is not successfully optimised and instead corresponds to a transition state - the optimisation must be repeated.

Low Frequencies Interpretation

The first row of 'low frequencies' are representative of rotational and translational modes of motion. If a negative (imaginary) low frequency is obtained it is indicative of the optimised structure corresponding to an energy maxima (transition state) as opposed to the desired energy minima (optimised structure). The first row of low frequencies should be reduced to the minimum possible value by implementing tight convergence criteria, otherwise the determined frequencies will attain a large degree of error hence rendering the data obtained effectively useless. These low frequencies essentially correlate to small variations in the optimised structure and will result in significant error for calculated frequencies, particularly those of comparatively low energy.

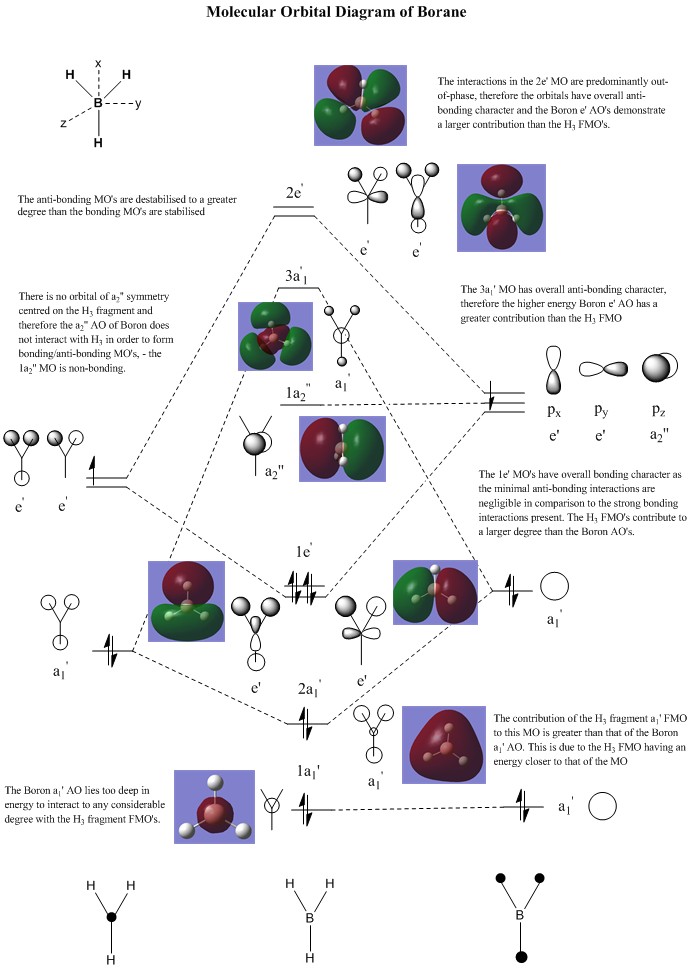
Borane Molecular Orbital Analysis

DOI:10042/147232

^[2]

Comparison of the Gaussian predicted Molecular Orbitals to those predicted by LCAO (Linear Combination of Atomic Orbitals) indicates that, qualitatively, LCAO is a relatively accurate method to predict the appearance and phase of Molecular Orbitals. Comparison of LCAO predictions and Gaussian prediction suggests the LCAO approach is particularly accurate in the examination of core Molecular Orbitals, with structure comparable to that of Atomic Orbitals. In this example the LCAO approach is particularly accurate due to the low difference in both size and electronegativity between Boron and Hydrogen. Therefore the Molecular Orbitals in Borane demonstrate a comparitively even distribution in both size and shape, without the need for consideration of the significant effects of polarisation or low overlap integrals. Despite this, as we probe higher energy (unoccupied) molecular orbitals the LCAO approach appears to decrease in accuracy, even for this relatively simple example. At high energy, where orbitals are often distributed over a much larger area, the Molecular Orbitals demonstrate a large degree of deformation to minimise disfavoured electrostatic interactions and the LCAO approach is no longer valid. In order to give a fair analysis of qualitative Molecular Orbital theory it would be necessary to perform the same analysis on more complex molecular systems.

Discussion of the accuracy and application of qualitative Molecular Orbital Theory

Qualitative Molecular Orbital (LCAO) theory predicts the interaction of the constituent atomic orbitals, assuming that only those of similar energy and identical symmetry may interact. In comparatively simple systems, such as the Borane example above, there are very few potential interactions as the number of constituent Atomic Orbitals is relatively low, therefore qualitative Molecular Orbital is a very useful tool in understanding and predicting the shape of Molecular Orbitals and compares favourably to the observed structures. As the energy of the Molecular Orbitals increases they become more diffuse and qualitative Molecular Orbital theory appears to break down to some degree.

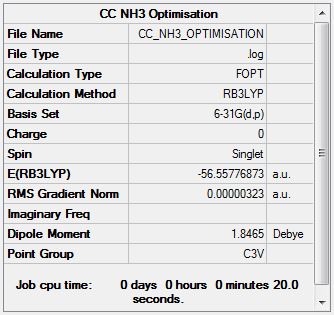
NH₃ Optimisation

Optimisation log file here

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000012 0.001800 YES RMS Displacement 0.000008 0.001200 YES Predicted change in Energy=-9.844303D-11 Optimization completed.	Optimised Ammonia Molecule

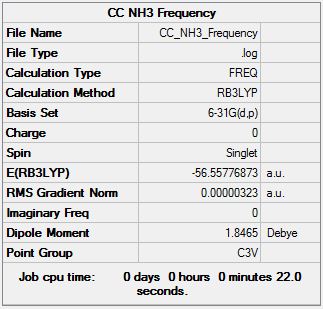
NH₃ Frequency Analysis

Frequency log file here

Summary Data	Low Modes
	Low frequencies --- -0.0129 -0.0012 0.0005 7.0724 8.1020 8.1023 Low frequencies --- 1089.3849 1693.9369 1693.9369

NH₃ Vibrational Spectrum

Wavenumber	Intensity	IR active	Type
1089	145	Yes	Bend (Wag)
1694	14	Yes (Very Slight)	Bend (Rocking)
1694	14	Yes (Very Slight)	Bend (Scissoring)
3461	1	No	Stretch (Symmetric)
3590	0	No	Stretch (Anti-Symmetric)
3590	0	No	Stretch (Anti-Symmetric)

NH₃ Population Analysis

DOI:10042/149391

NH₃ NBO Analysis

---

Specific NBO Charges

Atom	N	H
Charge	-1.125	0.375

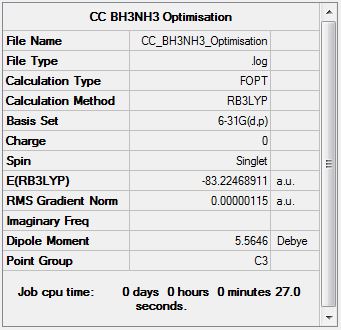
NH₃BH₃ Optimisation

Optimisation log file here

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000002 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000009 0.000060 YES RMS Displacement 0.000002 0.000040 YES Predicted change in Energy=-2.762787D-11 Optimization completed	Optimised Ammonia Borane Molecule

NH₃BH₃ Frequency Analysis

Frequency log file here

Summary Data	Low Modes
	Low frequencies --- -5.3337 -0.3634 -0.0553 -0.0005 0.9780 1.0863 Low frequencies --- 263.2953 632.9558 638.4563

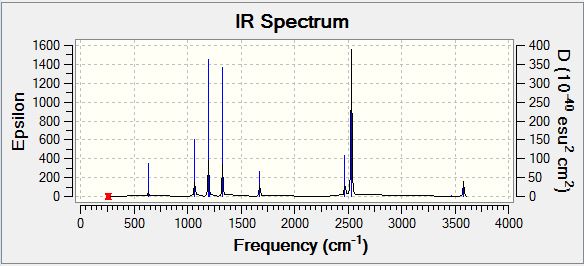
NH₃BH₃ Vibrational Spectrum

Wavenumber	Intensity	IR active	Type
263	0	No	Bend
633	14	Yes (Very Slight)	Stretch
638	4	No	Bend
638	4	No	Bend
1069	41	Yes	Bend
1069	41	Yes	Bend
1196	109	Yes	Bend
1204	3	No	Bend
1204	3	No	Bend
1329	114	Yes	Bend
1676	28	Yes	Bend
1676	28	Yes	Bend
2472	67	Yes	Stretch
2532	231	Yes	Stretch
2532	231	Yes	Stretch
3464	3	No	Stretch
3581	28	Yes	Stretch
3581	28	Yes	Stretch

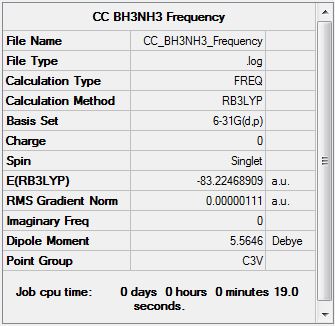
NH₃BH₃ Bond Energy

E(NH₃): -56.5577687 a.u.

E(BH₃): -26.6153236 a.u.

E(NH₃BH₃): -83.2246891 a.u.

NH₃BH₃ Dissociation Energy

ΔE = E(NH₃BH₃) - [E(NH₃) + E(BH₃)]

ΔE = -0.0515968 a.u.

ΔE = -135.47 kJmol^-1

This calculated bond dissociation energy appears to have a reasonable value. The bonding interaction would not be expected to be particularly weak due to the Boron centre having a large degree of electron deficiency and the Nitrogen centre possessing a readily available lone pair for donation to the electron deficient Boron centre. Conversely, the bonding would not be expected to be particularly strong as it is simply an adduct and there are no coulombic interactions as in the ionic bonding model. The calculated value lies in a similar range to the F-F bonding interaction (158 kJmol^-1) ^[9] discussed previously, which was concluded to be a medium strength bonding interaction as predicted here.

NH₃BH₃ Bond Strength

The NH₃BH₃ adduct clearly demonstrates attractive interactions strong enough to be considered a bonding interaction, the definition of which was discussed previously. This is evidenced by the relatively large dissociation energy calculated above (-135.47 kJmol^-1), however, the strength of a bond is clearly a somewhat qualitative quantity, requiring comparison to various interactions ranging from extremely weak hydrogen-bonding interactions to very strong ionic bonding interactions. In comparison to these interactions, the NH₃BH₃ interaction is clearly must stronger than hydrogen-bonding interactions (H₂O: 23.3 kJmol^-1) ^[10], similar in strength to the weakly covalent F-F bonding interaction (158 kJmol^-1) ^[9] and much weaker than strong ionic or even strong covalent bonding interactions such as the N-N triple bond in diatomic Nitrogen (941 kJmol^-1) ^[9]. Therefore it can be reasonably concluded that the NH₃BH₃ bonding interaction is of medium strength.

Lewis Acids and Bases Project Section

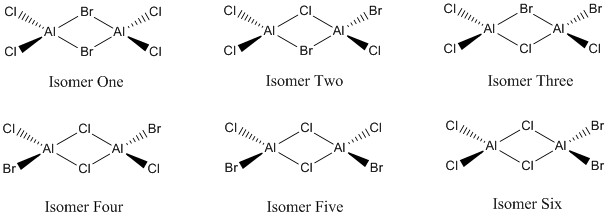
The following project section of this report aims to analyse the relative stability and bonding interactions in the six possible isomers of Al₂Cl₄Br₂, a Lewis Acid, via the application of Molecular Orbital theory. Traditionally bonding has been denoted by the Lewis methodology, with a single line representing the sharing of two electrons between the bonding atoms. However, this simplistic Lewis structure assumes all bond to be 2c-2e, which we now know to be inaccurate due to the observation of multi-centre bonding in species such as B₂H₆. In order to explain these complex bonding systems it is necessary to apply Molecular Orbital theory. First we shall consider the B₂H₆ species mentioned previously, the most notable example of 3c-2e bonding, identified by Longuet-Higgins in 1943. Previously the structure of B₂H₆ had eluded chemists for many years after it had been first synthesised in the 19th century. Longuet-Higgins proposed the following structure of D₂H symmetry in which the bridging hydrogens exhibit 3c-2e bonding:

It wasn't until after the pioneering advancement of Molecular Orbital theory that the Longuet-Higgins structure could be confirmed as although it correlated perfectly to the two-fold symmetry indicated by the IR spectrum, it failed to explain the presence of a B-B vibrational mode. This bonding interaction has now been confirmed via Molecular Orbital theory, supporting the currently accepted Longuet-Higgins dimeric structure which, as mentioned previously, exhibits multi-centre bonding interactions. The Al₂Cl₄Br₂ species discussed in the following analysis bears many similarities to B₂H₆, both being Lewis acidic dimeric species. The six isomeric variants of Al₂Cl₄Br₂ analysed are displayed below:

It is worthy of note that Isomers Two and Three are enantiomeric species and hence would be expected to have the same optimised energy.

Al₂Cl₄Br₂ Optimisation and Frequency Analysis

Optimisation analysis was completed for all of the isomers presented above and the results are demonstrated below, along with those of the frequency analysis. It was important to perform the optimisation analysis utilising the same basis set for each isomer, for the reasons discussed previously, such that the results could then be reasonably compared. Aluminium and Chlorine atoms were optimised using the 6-31G(d,P) basis set, however, it was necessary to use pseudo-potentials in the optimisation of Bromine, utilising the LanL2DZ basis set. Before each calculation was performed the point group (symmetry) of the molecule was restricted with 'very tight' criteria.

As previously, the structures were optimised to a point of zero gradient on the potential energy surface (an energy minima/maxima) and the log files examined in order to ensure convergence was complete. The calculations were performed through SCAN and the log file data presented below in DSpace. The Born-Oppenheimer approximation is assumed accurate during all calculations i.e. the electronic energy levels of the molecule are independent of nuclear motion and electron density adjusts instantaneously to any motion of the nuclei.

Frequency analysis was performed on each of the optimised structures through SCAN, utilising the same basis sets as described previously. Again the log file data was published via DSpace and before calculation the point group (symmetry) of the molecule was restricted with 'very tight' criteria. The low frequencies are presented below and inspected to ensure the values are reasonable and an optimised structure had been obtained as opposed to a transition state structure. The corresponding vibrational frequencies are presented below, along with the vibrational spectra of the respective isomers.

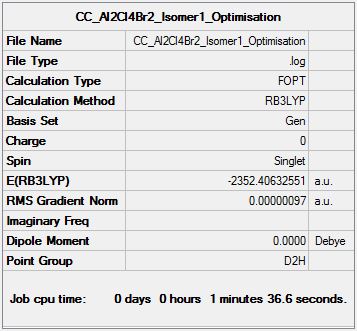
Al₂Cl₄Br₂ Isomer One

Optimisation Analysis

Optimisation log file DOI:10042/152945

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000002 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000031 0.000060 YES RMS Displacement 0.000011 0.000040 YES Predicted change in Energy=-9.855541D-11 Optimization completed	Optimised Isomer One

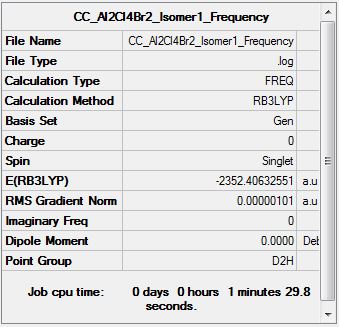
Frequency Analysis

Frequency log file DOI:10042/147655

Summary Data	Low Modes
	Low frequencies --- -0.7423 -0.0028 -0.0021 -0.0019 1.3552 1.4532 Low frequencies --- 16.0780 63.6252 86.1130

Vibrational Spectrum

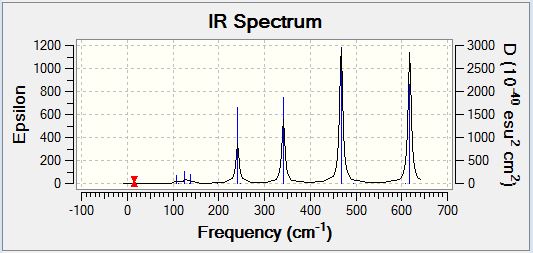
Wavenumber	Intensity	IR active	Type
16	0	No	Bend
64	0	No	Bend
86	0	No	Bend
87	0	No	Bend
108	5	Yes (Very Slight)	Bend
111	0	No	Bend
126	8	Yes (Very Slight)	Bend
135	0	No	Bend
138	7	Yes (Very Slight)	Bend
163	0	No	Bend
197	0	No	Stretch
241	100	Yes	Stretch
247	0	No	Stretch
341	160	Yes	Stretch
468	346	Yes	Stretch
494	0	No	Stretch
609	0	No	Stretch
617	332	Yes	Stretch

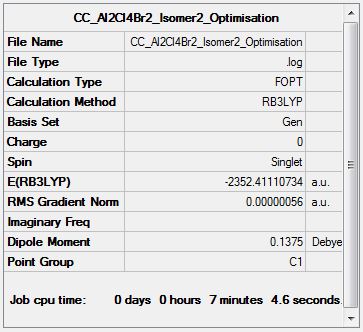
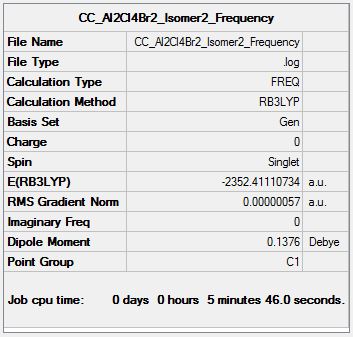
Al₂Cl₄Br₂ Isomer Two

Optimisation Analysis

Optimisation log file DOI:10042/153020

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000000 0.000015 YES RMS Force 0.000000 0.000010 YES Maximum Displacement 0.000012 0.000060 YES RMS Displacement 0.000004 0.000040 YES Predicted change in Energy=-5.563114D-12 Optimization completed	Optimised Isomer Two

Frequency Analysis

Frequency log file DOI:10042/153050

Summary Data	Low Modes
	Low frequencies --- -0.0020 -0.0019 -0.0008 0.0802 1.1112 1.8126 Low frequencies --- 16.9440 55.9196 80.0644

Vibrational Spectrum

Wavenumber	Intensity	IR active	Type
17	0	No	Bend
56	0	No	Bend
80	0	No	Bend
92	0	No	Bend
107	0	No	Bend
110	5	Yes (Very Slight)	Bend
121	8	Yes (Very Slight)	Bend
149	5	Yes (Very Slight)	Bend
154	6	Yes (Very Slight)	Bend
186	1	No	Bend
211	21	Yes (Very Slight)	Stretch
257	10	Yes (Very SLight)	Stretch
289	48	Yes	Stretch
384	153	Yes	Stretch
424	274	Yes	Stretch
493	107	No	Stretch
575	122	No	Stretch
615	197	Yes	Stretch

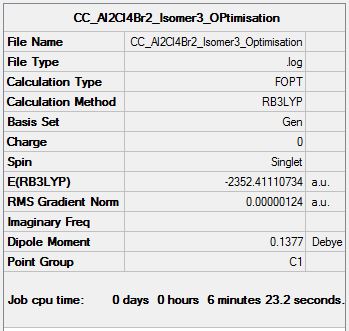
Al₂Cl₄Br₂ Isomer Three

Optimisation Analysis

Optimisation log file DOI:10042/154976

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000002 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000059 0.000060 YES RMS Displacement 0.000022 0.000040 YES Predicted change in Energy=-2.499783D-10 Optimization completed	Optimised Isomer Three

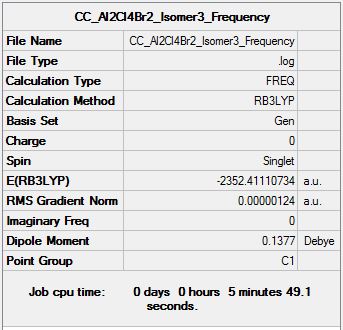
Frequency Analysis

Frequency log file DOI:10042/154995

Summary Data	Low Modes
	Low frequencies --- -0.0020 0.0021 0.0024 0.1617 1.1019 1.7944 Low frequencies --- 16.9437 55.9195 80.0649

Vibrational Spectrum

Wavenumber	Intensity	IR active	Type
17	0	No	Bend
56	0	No	Bend
80	0	No	Bend
92	1	No	Bend
107	0	No	Bend
110	5	Yes (Very Slight)	Bend
121	8	Yes (Very Slight)	Bend
149	5	Yes (Very Slight)	Bend
154	6	Yes (Very Slight)	Bend
186	1	No	Bend
211	21	Yes (Very Slight)	Stretch
257	10	Yes (Very Slight)	Stretch
289	48	Yes	Stretch
384	153	Yes	Stretch
424	274	Yes	Stretch
493	107	No	Stretch
575	122	No	Stretch
615	197	Yes	Stretch

Al₂Cl₄Br₂ Isomer Four

Optimisation Analysis

Optimisation log file DOI:10042/155132

Summary Data	Convergence	Jmol
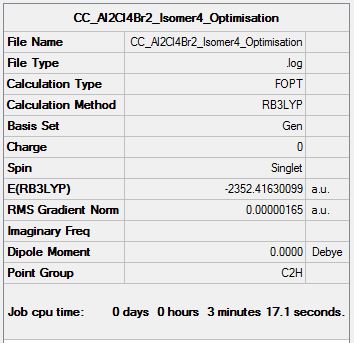
	Item Value Threshold Converged? Maximum Force 0.000005 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000045 0.000060 YES RMS Displacement 0.000016 0.000040 YES Predicted change in Energy=-1.947218D-10 Optimization completed.	Optimised Isomer Four

Frequency Analysis

Frequency log file DOI:10042/155167

Summary Data	Low Modes
	Low frequencies --- -0.8374 -0.7355 -0.0035 -0.0034 -0.0030 2.1140 Low frequencies --- 18.3005 49.2131 72.9022

Vibrational Spectrum

Wavenumber	Intensity	IR active	Type
18	0	No	Bend
49	0	No	Bend
73	0	No	Bend
105	0	No	Bend
109	0	No	Bend
117	9	Yes (Very Slight)	Bend
120	13	Yes (Very Slight)	Bend
157	0	No	Bend
159	6	Yes (Very Slight)	Bend
192	0	No	Bend
263	0	No	Stretch
280	29	Yes	Stretch
308	0	No	Stretch
413	149	Yes	Stretch
421	438	Yes	Stretch
459	0	No	Stretch
575	0	No	Stretch
580	316	Yes	Stretch

Al₂Cl₄Br₂ Isomer Five

Optimisation Analysis

Optimisation log file DOI:10042/155197

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000001 0.000015 YES RMS Force 0.000000 0.000010 YES Maximum Displacement 0.000035 0.000060 YES RMS Displacement 0.000012 0.000040 YES Predicted change in Energy=-2.764540D-11 Optimization completed	Optimised Isomer Five

Frequency Analysis

Frequency log file DOI:10042/155225

Summary Data	Low Modes
	Low frequencies --- -1.6557 -0.9915 -0.0044 -0.0037 -0.0035 1.6221 Low frequencies --- 17.4359 51.1215 78.5165

Vibrational Spectrum

Wavenumber	Intensity	IR active	Type
17	0	No	Bend
51	0	No	Bend
79	0	No	Bend
99	0	No	Bend
103	3	No	Bend
121	13	Yes (Very Slight)	Bend
123	6	Yes (Very Slight)	Bend
157	0	No	Bend
158	5	Yes (Very Slight)	Bend
194	2	No	Bend
263	0	No	Stretch
279	26	Yes	Stretch
308	2	No	Stretch
413	149	Yes	Stretch
420	410	Yes	Stretch
461	35	No	Stretch
571	33	No	Stretch
583	277	Yes	Stretch

Al₂Cl₄Br₂ Isomer Six

Optimisation Analysis

Optimisation log file DOI:10042/155261

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000004 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000030 0.000060 YES RMS Displacement 0.000010 0.000040 YES Predicted change in Energy=-1.215406D-10 Optimization completed	Optimised Isomer Six

Frequency Analysis

Frequency log file DOI:10042/155277

Summary Data	Low Modes
	Low frequencies --- -0.8328 -0.5970 -0.0051 -0.0050 -0.0048 2.0363 Low frequencies --- 18.6229 51.2070 72.2009

Vibrational Spectrum

Wavenumber	Intensity	IR active	Type
19	0	No	Bend
51	0	No	Bend
72	1	No	Bend
98	0	No	Bend
112	0	No	Bend
112	8	Yes (Very Slight)	Bend
120	11	Yes (Very Slight)	Bend
160	1	No	Bend
166	7	Yes (Very Slight)	Bend
187	2	No	Bend
263	0	No	Bend
271	14	Yes (Very Slight)	Stretch
323	41	Yes	Stretch
413	150	Yes	Stretch
418	309	Yes	Stretch
495	134	Yes	Stretch
503	105	Yes	Stretch
616	177	Yes	Stretch

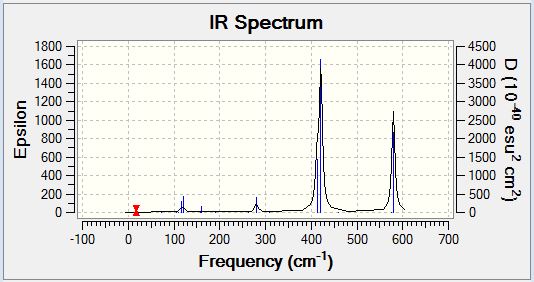
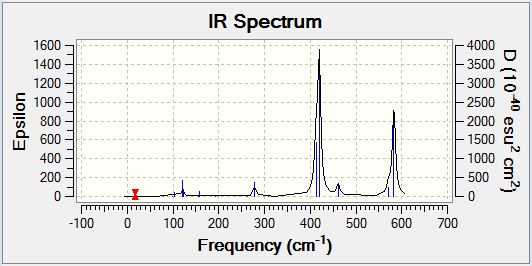
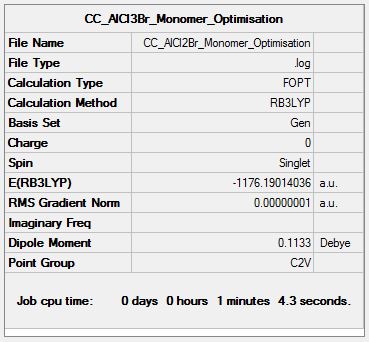
AlCl₂Br Monomer

Optimisation Analysis

Optimisation log file DOI:10042/155309

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000000 0.000015 YES RMS Force 0.000000 0.000010 YES Maximum Displacement 0.000000 0.000060 YES RMS Displacement 0.000000 0.000040 YES Predicted change in Energy=-1.008890D-16 Optimization completed	Optimised Monomer

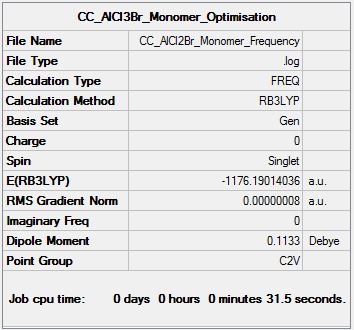
Frequency Analysis

Frequency log file DOI:10042/155325

Summary Data	Low Modes
	Low frequencies --- 0.0008 0.0022 0.0030 1.8664 1.8732 3.5921 Low frequencies --- 120.7378 133.8464 185.7655

Vibrational Spectrum

Wavenumber	Intensity	IR active	Type
121	5	Yes (Very Slight)	Bend
134	6	Yes (Very Slight)	Bend
186	33	Yes	Bend
314	7	Yes (Very Slight)	Stretch
552	174	Yes	Stretch
614	186	No	Stretch

Isomer Energy Comparison

	Isomer One	Isomer Two	Isomer Three	Isomer Four	Isomer Five	Isomer Six
Etot (a.u.)	(-)2352.4063255	(-)2352.4111073	(-)2352.4111073	(-)2352.4163010	(-)2352.4162785	(-)2352.4163437

The absolute energy values stated above are of little use, as discussed previously, it is the relative energies of the Isomers which are of primary interest. In order to compare these values the lowest energy isomer is assigned an energy of 0 kJmol^-1, the energy of the other isomers are stated relative to this:

Isomer One: 26.30 kJmol^-1

Isomer Two: 13.75 kJmol^-1

Isomer Three: 13.75 kJmol^-1

Isomer Four: 0.11 kJmol^-1

Isomer Five: 0.17 kJmol^-1

Isomer Six: 0.00 kJmol^-1

The data stated above clearly indicates the energy of Isomer Six is the lowest and therefore has a greater degree of relative stability. However, the Gaussian calculations can yield an error of up to ±10 kJmol^-1 in the relative energies and as a result it cannot reasonably be concluded that Isomer Six is significantly more stable than either Isomer Four or Five, simply that these three isomers are stable in comparison to Isomers One, Two and Three. Despite this, the remainder of analysis will be completed with the assumption that the above calculations are correct and therefore Isomer Six is the most stable (lowest energy). It should also be noted that Isomers Two and Three are enantiomeric in nature, as indicated by their identical calculated energies above. Therefore they differ in their interaction with plane polarised light but their physical properties would be identical.

Discussion of Factors affecting the relative stability of the Isomers

Dimerisation

Even before the discussion of the individual isomeric species of Al₂Cl₄Br₂ it is necessary to rationalise why this molecule exists in dimeric form as opposed to monomeric form. In Boron species B₂H₆ is unusual in regard to being dimeric as opposed to monomeric, whereas Aluminium species (such as the one in question) are more commonly observed in this dimeric form. Boron and Aluminium are both present in group 13 of the periodic table and therefore have a very similar electronic structure, however, the primary difference between the two is the marked increase in size as we descend the group. Initially we will probe the structure of BBr₃ discussed in section one of this report. This is a trigonal planar Boron species in which the central Boron atom is electron deficient (Six valence electrons), however, the Boron electron deficiency is somewhat relieved by π-stabilisation. This is possible due to the effective orbital overlap of the vacant p-orbital of the Boron centre and the occupied p-orbital (lone pair) of the Bromine substituents. Donation of electron density into the vacant p-orbital of the Boron centre stabilises the molecule, explaining the relatively high stability of the monomeric species of Boron. In contrast, Aluminium has a larger principal quantum number and therefore the Al-Br bond length would be significantly larger. The strength of π-bonding decreases dramatically with respect to distance due to the decreased orbital overlap and therefore the degree of π-stabilisation possible is much reduced in monomeric Aluminium species in comparison to Boron species. As a result Aluminium species, such as that in question, are much more likely to occur in dimeric form.

Effect of the position of the Bromine atoms on the energy

The electron deficiency of the Aluminium centre has been discussed in detail above, with reference as to why the Aluminium species in question tends to occur in dimeric form whereas Boron species tend to occur in monomeric form (with the significant exception of B₂H₆. The reasoning for this was the reduced π-stabilisation possible in Aluminium species, such that the formation of a dimer is a more effective way in which to reduce the electron deficiency of the Aluminium centre. This argument can be extended to say that the isomer of Al₂Cl₄Br₂ which is most stable will be the one which most effectively relieves the electron deficiency on Aluminium - here we will discuss how changing the position of the Bromine/Chlorine atoms can achieve this.

Electronegativity

Firstly, we will probe the Aluminium bridging bonds which can be formally denoted as 3c-2e bonding interactions. This interaction actually consists of the σ-donation of the lone pair electron density on the Halogen to the electron deficient Aluminium, formally a dative bond. Therefore it would be predicted that Isomer One, in which both bridging atoms are Bromine, would be the lowest energy isomer due to the lower electronegativity of Bromine in comparison to Chlorine indicating that it would be more willing to donate electron density to the Aluminium. However, our calculations clearly prove that this is not the case and the lowest energy isomer is one in which both of the bridging atoms are Chlorine. It is immediately clear that there are many other factors affecting the relative stability of the isomers and an analysis based purely on electronegativity arguments is inadequate. Although the availability of the σ-lone pair on Bromine is greater than for Chlorine, there are other effects which the results indicate must dominate.

Orbital Overlap

Despite the conclusion above that many factors must affect the relative isomer stabilities, we will continue to restrict ourselves to considering the bridging region. It is important to consider the relative degree of orbital overlap between the Aluminium centre and the lone pair of the halogen species. Although the electronegativity of Bromine is lower and therefore the lone pairs are more available for σ-donation, it would be predicted that the orbital overlap between Aluminium and Bromine would be worse than that of Aluminium and Chlorine. This conclusion is obtained from an orbital size argument due to the increased principal quantum number of Bromine, resulting in the orbital size match of Al-Br being poor in comparison Al-Cl where the overlap is more effective due to the more contracted nature of the Chlorine valence orbitals. In a more theoretical sense, it would be expected that orbitals of a similar size would have a greater overlap integral and as Aluminium and Chlorine are in the same group of the periodic table this would be the preferred interaction. This yields the opposite conclusion to the electronegativity argument above, predicting that the most stable isomer would have the two bridging atoms both being Chlorine (Isomers Four, Five and Six meet this criteria). This prediction clearly matches the Gaussian prediction as the calculated energies of Isomers Four, Five and Six are significantly lower than those of Isomer One, Two and Three where there is a bridging Bromine present.

Other Factors

There are still many other factors influencing the relative stability of the isomers discussed, many of which we will not have time to discuss in detail here. An important interaction to mention is the potential interaction of the two Aluminium centres in the dimeric structures. The strength of this interaction is affected significantly by the length of the bridging bonds to maximise the effeciency of orbitals overlap between the two (maximise the overlap integral). Clearly the shorter Al-Cl bridging bonds allow closer approach of the two Aluminium centres, increasing the overlap integral and hence strength of this interaction. It is often difficult to interpret the hybridisation of the Aluminium centre as the IR spectrum indicates that the Aluminium adopts sp² hybridisation in contrast to the bond angles which indicate sp³ hybridisation. It is also worthy of note that Al³⁺ has extremely high charge density and is therefore a highly polarising cation. This results in the bridging bonds being highly polarised, particularly in the case of bridging Bromine which is more polarisable than Chlorine.

Lessons learnt from the Optimisation

It is important to realise that although the orbital overlap effect appears to dominate in determining the structure of the most stable isomer, there is likely a significant contribution from all the factors discussed above. Within the realms of error, the Gaussian analysis yielded the conclusion that Isomers Four, Five and Six are essentially degenerate and of significantly lower energy than Isomers One, Two and Three. The most notable characteristic of these isomers is the fact that they all contain two bridging Chlorine atoms. This allows us to reasonably reach the conclusion stated above that the dominant factor in determining the stability of the isomers is the efficiency of orbital overlap between the Aluminium centre and the bridging halogen. By comparison of the energy of Isomers Four, Five and Six to Isomers One, Two and Three it can be seen that the introduction of a bridging Bromine destabilises the molecule by approximately 13 kJmol^-1 and the introduction of a second bridging Bromine destabilises the molecule by a further 13 kJmol^-1. Therefore it can be concluded that bridging Chlorine is approximately 13 kJmol^-1 more stable than bridging Bromine.

Potential for Further Study

In order to improve the analysis further it would be desired to quantify the availability of the halogen lone pair and overlap integrals in the bridging region to give a more accurate picture of the contributing atomic orbitals. It could also be investigated as to whether the variation of halogen position would yield the same results in species with different metal centres.

Product Stability in comparison to Isolated Monomers

The relative stability of the dimeric structure can be determined via comparison to the energy of two isolated monomer species. In theory the dimeric structure ought to be lower in energy than two isolated monomers due to the stabilising interactions discussed above. In order to complete this analysis, the energy of the AlCl₂Br monomer was determined above. This monomer was most suitable as it can clearly be seen how two equivalents of this monomeric species may been combined to yield Isomers One, Two, Three, Four and Five directly. It is less clear how the lowest energy Isomer Six may be obtained from this monomeric species, however, dynamic exchange of the halogen substituents in the dimeric structures can explain its formation.

The dissociation energy of the lowest energy Isomer Six to form the two monomeric species can be calculated from the results obtained above as below:

ΔE = E (Al₂Cl₄Br₂) - 2E (AlCl₂Br)

ΔE = -0.0360630 a.u.

Therefore it can be concluded that the optimised dimeric form of Al₂Cl₄Br₂ is 0.0360630 a.u. more stable than the optimised monomeric structure. This provides evidence for the predictions described previously that the dimeric structure is more stable than two isolated monomers due to the interactions discussed above. It would be possible to extend this analysis further to provide evidence for the hypothesis that dimerisation occurs in Aluminium species more readily than in Boron species due to the decreased efficiency of the π-stabilisation. In order to do this analogous Boron centred dimeric/monomeric species would have to be set up and optimised to establish their relative energy and it would be expected that via the same dissociation energy analysis above it could be concluded that the monomeric species are actually more stable than the dimeric structure.

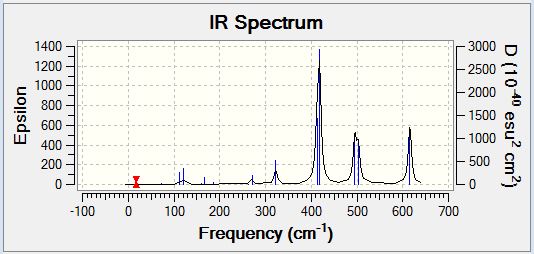
Comparison of the number of bands in IR Spectra

In order to understand why some IR spectra contain more peaks than other it is important to understand what makes a vibrational mode IR active. The primary tool which can be used to rationalise this is the following IR selection rule; in order for a vibrational mode to be IR active, it must result in a variation in the molecular dipole moment. In addition to this the intensity of the peak in the IR spectrum is dependent on the magnitude of the variation in molecular dipole moment. Therefore, if a vibrational mode exists which does not cause a variation in the molecular dipole moment it will not be observed in the IR spectrum of the molecule, however, these vibrational modes can be observed by Raman spectroscopy. One of the primary factors affecting whether vibrational modes will result in a variation of the molecular dipole moment is the degree of symmetry in the molecule i.e. if the molecule has a large degree of symmetry it will have few IR active vibrational modes and vice-versa. In order to rationalise the number of peaks observed in the IR spectra of the optimised isomers it is necessary to analyse their symmetry therefore the point groups of all the analysed isomers are presented below:

	Isomer One	Isomer Two	Isomer Three	Isomer Four	Isomer Five	Isomer Six
Point Group	D2H	C1	C1	C2H	C2V	C2V

By analysis of the point groups in the table above it would be predicted that Isomers Two and Three would have the greatest number of IR active vibrational modes due to their inherent lack of symmetry. The primary effect of the lack of symmetry in these isomers is that both the symmetric and anti-symmetric stretches will be IR active, assuming that during these vibrational modes there is translational motion of all constituent atoms. Translational motion of all atoms in these isomers can't be counteracted by equal motion elsewhere in the molecule due to the lack of mirror planes across the molecule and therefore any vibrational modes which meet this criteria are IR active. This explains the observation of so many IR active modes in the spectra of Isomers Two and Three, however, it does not provide any explanation as to their relative intensities. The intensities of many of the observed peaks are relatively low, indicating that the variation in molecular dipole moment as a result of the vibrational modes is comparatively low. This may be rationalised by the similarity in the electronic properties of Bromine and Chlorine, therefore even relatively large amounts of translational motion cause small variations in molecular dipole moment and hence the peaks are of comparatively low intensity.

At the other end of the spectrum Isomer One has a large degree of molecular symmetry (D₂H), exhibiting numerous planes of symmetry. Therefore it follows from the arguments displayed above that Isomer One would produce comparatively few IR active vibrational modes in the IR spectrum. Just to reiterate the points above, this is due translational motion of atoms being completely cancelled by symmetric translational motion on the other side of the symmetry planes, resulting in no net change in dipole moment for many of the vibrational modes. The remaining isomers are all of medium symmetry and therefore display an intermediate number of IR active vibrational modes in their respective spectra. It is worthy of note that Isomers Five and Six, as shown above, are of the same symmetry (point group) and as they also have an equal number of constituent atoms, an equal number of IR active vibrational modes are observed in their respective IR spectra.

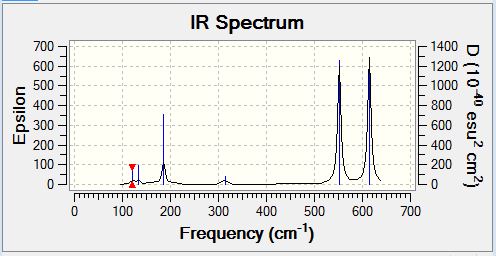
Effect of the position of the Bromine atoms on the IR Spectra

Below are tabulated the key vibrational frequencies relating to Al-Br stretching vibrational modes (terminal and bridging) observed across all of the Isomers of Al₂Cl₄Br₂ investigated above. This is followed by discussion and comparison of the Al-Br stretching modes in each of the isomers discussed with particular reference to the position and nature of these vibrational modes.

Isomer #	Wavenumber	Intensity	Vibrational Mode	Terminal/Bridging
One	241	100	Stretch (Anti-symmetric)	Bridging
One	247	0	Stretch (Symmetric)	Bridging
Two	257	10	Stretch (Anti-symmetric)	Terminal/Bridging
Two	289	48	Stretch (Symmetric)	Terminal/Bridging
Three	257	10	Stretch (Anti-symmetric)	Terminal/Bridging
Three	289	48	Stretch (Symmetric)	Terminal/Bridging
Four	421	438	Stretch (Anti-symmetric)	Terminal
Four	459	0	Stretch (Symmetric)	Terminal
Five	420	410	Stretch (Anti-symmetric)	Terminal
Five	461	35	Stretch (Symmetric)	Terminal
Six	418	309	Stretch (Symmetric)	Terminal
Six	495	134	Stretch (Anti-symmetric)	Terminal

It can clearly be observed from the table above that in general terminal Al-Br stretching frequencies are of significantly higher wavenumber that bridging stretching frequencies. The explanation of this trend can be quite simply derived by analysis of the respective bonds, with particular reference to the strength of the bond. It was stated previously that the vibrational frequency is related to the force constant (it is proportional the square root) and the force constant of a bond is in turn related to the bond strength. Therefore the stronger a bond, the greater its vibrational frequency (wavenumber). It has previously been discussed that the bridging bonds are formally 3c-2e, whereas the terminal bonds are more traditional 2c-2e bonds - it would therefore be expected that the terminal bonds are stronger due to the increased electron density. In turn it follows that terminal bonds would therefore correspond to larger vibrational frequencies. Another point to note that the stretching frequencies observed in the vibrational spectrum of Isomers Two and Three are identical, this is due to them being enantiomeric and hence displaying identical physical properties.

It is also interesting to note the differences between symmetric and anti-symmetric stretching vibrational modes, both of which are observed for the respective Al-Br vibrational modes of each isomer (terminal or bridging). There is no immediately apparent trend in this regard as the one which is accompanied by a higher vibrational frequency is different for each isomer. By comparison of the wavenumber for the terminal and bridging Al-Br stretches it can, however, be observed that all the terminal Al-Br stretches are similar in magnitude whereas there is a marked increase in the variation for bridging Al-Br stretches. Therefore it can be postulated that movement of Bromine between the terminal positions has a comparatively small effect on vibrational frequency when compared to movement of Bromine to the bridging positions (one bridging Bromine versus two bridging Bromines etc.).

Previously it has been established that the primary factor affecting the relative stability of the different isomeric species was the nature of the bridging halogen. We will now aim to confirm this hypothesis by comparison of the bridging Al-Cl stretching frequencies of Isomer six (most stable) and the bridging Al-Br stretches of Isomer One (least stable). In the vibrational spectrum of Isomer Six the anti-symmetric stretching frequency is observed at 271 cm^-1 with the corresponding symmetric stretching frequency observed at 323 cm^-1. In contrast, the anti-symmetric stretching frequency in Isomer One is observed at 241 cm^-1 with the corresponding symmetric strecthing frequency observed at 247 cm^-1. It is immediately evident that the Al-Cl stretching frequencies of Isomer Six are at significantly higher wavenumber than the Al-Br stretching frequencies of Isomer One, indicating that the Al-Cl bridging bonds in Isomer six are stronger and providing evidence for our previous hypothesis. The reasoning behind this increased bridging bond strength was discussed in detail above with the conclusion that the dominating factor was the increased efficiency of orbital overlap in the Al-Cl bridging bonds. Further evidence is supplied by analysis of the Al-Br stretching frequencies of Isomers One (Two bridging Bromines) and Two (One bridging Bromine, One bridging Chlorine). The stretching frequencies of Isomer One are 241 cm^-1 (anti-symmetric) and 247 cm^-1 (symmetric) in comparison to the stretching frequencies of Isomer Two which are 257 cm^-1 (anti-symmetric) and 289 cm^-1 (symmetric). It can clearly be observed that the stretching frequencies of Isomer Two are significantly greater than those of Isomer One, providing further evidence for the increased strength of the Al-Cl bridging bond relative to the Al-Br bridging bond.

The next stage of our analysis will be to examine the relative intensities of the Al-Br stretching frequencies in the IR spectra. It is immediately evident that Isomers One and Four respectively have IR inactive symmetric stretching frequencies, illustrated by their peaks of zero intensity. As explained previously, from this we can conclude that these vibrational modes do not yield a variation in the molecular dipole moment. However, the anti-symmetric stretching frequencies in all cases were IR active and hence must cause a variation in molecular dipole moment. The second important thing to observe in the data above is that in general terminal stretching frequencies appear to be of higher intensity in the vibrational spectrum and therefore must correspond to a greater variation in the molecular dipole moment, perhaps due to the increased translational motion of the Aluminium atoms in the terminal stretches (visualised by Gaussian). Conversely, when the stretching frequencies are visualised, during the bridging stretching frequencies the Aluminium centres remain essentially motionless and as they possess a large proprtion of the electron density there is a comparatively minimal variation in molecular dipole moment.

Molecular Orbital Analysis of Al₂Cl₄Br₂ Isomer Six

Population log file DOI:10042/157824

A Population analysis was performed on Al₂Cl₄Br₂ Isomer Six, obtaining the Molecular Orbitals from the formatted checkpoint file above, some of which are visualised below. The following analysis aims to thoroughly analyse the bonding character of various occupied, non-core Molecular Orbitals via analysis of the orbital interactions. The orbitals presented below range in character from strongly bonding to strongly anti-bonding and offer an important insight to the comparative stability of Isomer Six. Each Molecular Orbital is represented in two forms, one demonstrating the individual atomic orbital contributions to the molecular orbitals and one displaying the optimised Molecular Orbital predicted by Gaussian.

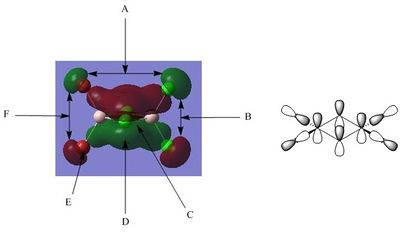
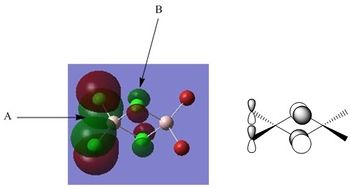
Molecular Orbital Thirty-Seven

A - This refers to the large bonding region of the molecular orbital on the left. This is clearly a strong bonding interaction as this section of the Molecular Orbital consists of a single phase and there are no nodes/nodal planes observed. The appearance of this section could be explained by the in-phase interaction of the Aluminium 3s orbital with the Chlorine 3p orbitals (both bridging and terminal). The nodal planes of the Chlorine 3p orbitals are clearly observed as indicated by the change in phase either side of the Chlorine atomic centres. The distribution of electron density in this bonding region appears to be relatively equal, perhaps due to the high electronegativity of Chlorine and the highly polarising Aluminium centre.

B - There is a Nodal plane here which passes through the centre of the bridging Chlorine and is present due to the contribution of the bridging Chlorine p-orbitals. It is worthy of note that there is significant distortion of the p-orbitals such that the electron density of the bridging chlorines is shifted somewhat towards the side of the molecule possessing terminal Chlorine atoms. This could potentially be explained by the increased electron deficiency of the Aluminium centre on this side due to the reduced availability of the Chlorine lone pairs in comparison to the Bromine lone pairs and Chlorines greater electronegativity. The distortion of the bridging Chlorine p-orbitals results in increased overlap of the Chlorine 3p-orbital and the Aluminium 3s-orbital, stabilising the electron deficient Aluminium centre. It is also observed in this region that there is an anti-bonding interaction between the large out-of-phase regions of the Molecular Orbital, primarily between the Aluminium centres. It is observed that the section of the Molecular Orbital on the right is somewhat distorted away from the left, perhaps to reduce this anti-bonding interaction. The distortion of the bridging Chlorine p-orbitals is responsible for the separation of the two out-of-phase regions and therefore reduces the strength of this anti-bonding interaction.

C - Interaction C is a comparatively weak in-phase (bonding) through-space interaction between the p-orbitals of the terminal Bromine atoms. An analogous interaction is present, but not labelled, between the p-orbitals of the terminal Chlorine atoms on the other side of the molecule.

D - There is a Nodal plane present which passes directly through the centre of the terminal Bromine atoms (both terminal Bromine atoms exhibit this behaviour). The Nodal plane in this example is from the Bromine p-orbital. Interaction E is analogous but refers to the same phenomena occurring on terminal Chlorine.

E - There is a Nodal plane present which passes directly through the centre of the terminal Chlorine atoms (both terminal Chlorine atoms exhibit this behaviour). The Nodal plane in this example is from the Chlorine p-orbital. Interaction D is analogous but refers to the same phenomena occurring on terminal Bromine.

F - This is the large bonding region to the right of the molecule, which was mentioned in B to interact out-of-phase with the large bonding region to the left. The constituent Atomic Orbitals are similar to those discussed in A , however, the resultant region of electron density is much different in shape to that of A. The electron density is distorted towards the electron deficient Aluminium with little electron density remaining localised on Bromine due to the increased polarisability of Bromine in comparison to Chlorine.

This Molecular Orbital is the lowest energy no-core orbital and from the analysis performed above it can be concluded to have overall bonding character. There are two regions of strong bonding character in the Molecular Orbital above, consisting of strong direct in-phase overlap between the halogen 3p-orbitals (both bridging and terminal) and the 3s-orbitals of Aluminium. The orbital overlap in these regions is relatively efficient and therefore results in a large degree of stabilisation of the Molecular Orbital. In addition to this, there are much weaker through-space bonding interactions between the 3p-orbitals of the terminal halogens, further stabilising the Molecular Orbital. However, there is still a certain degree of anti-bonding character in this Molecular Orbital, located in the bridging region between the two bonding regions discussed above. Although initial inspection might suggest that this out-of-phase interaction may be strongly anti-bonding, it must be noted that the constituent bridging Chlorine 3p-orbitals have an inherent change of phase and therefore there is no anti-bonding interaction at these points. The only constituent Atomic Orbitals which do interact out-of-phase are the Aluminium 3s-orbitals which have a relatively large spacial separation and as they are primarily core-like orbitals their anti-bonding interaction will be comparatively weak and the Molecular Orbitals can be concluded to have overall bonding character.

Molecular Orbital Fourty

A - This is a weak through-space bonding interaction between the 3p-orbitals of terminal Chlorine and the 4p-orbitals of terminal Bromine. This interaction occurs over a comparatively large distance and is non-directional, therefore its strength is very weak, contributing little to the overall stabilisation of this Molecular Orbital. There is an analogous interaction on both the top and bottom faces of the molecule as shown.

B - There is a through-space anti-bonding interaction between the 4p-orbitals of the terminal Bromines. This interaction is somewhat stronger than the bonding interaction A due to the decreased separation of the interacting orbitals, however, it is still non-directional and therefore comparatively weak. This interaction is analogous to that described in F although interaction F will be somewhat stronger due to the increased contribution of the 3p-orbitals of Chlorine to the orbital as opposed to the 4p-orbitals of Bromine. This is due to the better energy match of the 3p-orbitals of Chlorine to the Molecular Orbital

C - It is important to note the presence of a nodal plane through the atomic centres of the central Aluminiums and the bridging Chlorines. This is characteristic of the π-interaction discussed below (D) and acts to raise the energy of the Molecular Orbital somewhat, due to its internuclear nature. In comparison, the nodes on the atomic centres of the terminal halogens (described in E) have very little impact on the overall energy of the orbital

D - Interaction D is a strong in-phase (bonding) π-interaction of the 3p-orbitals of the central Aluminiums and the 3p-orbitals of the bridging Chlorines. As mentioned previously, it is clearly a π-interaction due to the nature of the phase change through the centre of the molecule and therefore the interaction has quite good directionality. This bonding interaction, along with that described in E, dominate the overall bonding characteristics of the Molecular Orbital as they are the only through-bond interactions.

E - There is a strong in-phase (bonding) interaction between the 3p-orbitals of the central Aluminium and the 3p-orbitals of the seminal Chlorines. This interaction is of moderate strength as although it is through-bond, it is also of low-directionality compared to the π-interaction described in D. Despite this it still makes a large contribution to the overall stabilisation of the Molecular Orbital. There is an analogous interaction between the 3p-orbitals of central Aluminium and the 4p-orbitals of terminal Bromine. In addition, it is important to not the presence of nodes at the atomic centres of the terminal halogens. They are localised at the atomic centres and therefore have little effect on the overall energy of the orbital in comparison to the nodal plane (C).

F - There is a through-space anti-bonding interaction between the 3p-orbitals of the terminal Chlorines. This interaction is somewhat stronger than the bonding interaction A due to the decreased separation of the interacting orbitals, however, it is still non-directional and therefore comparatively weak. This interaction is analogous to that described in B although interaction F will be somewhat stronger due to the increased contribution of the 3p-orbitals of Chlorine to the orbital as opposed to the 4p-orbitals of Bromine. This is due to the better energy match of the 3p-orbitals of Chlorine to the Molecular Orbital.

The most important bonding interaction with respect to the bonding characteristics of this Molecular Orbital is the large region of electron density in the centre of the orbital due to in-phase (bonding) π-interactions between the 3p-orbitals of bridging Chlorine and the 3p-orbitals of the Aluminium centres. It is simple to classify this as a π-interaction due to the nature of the phase change in this region; there is clearly a nodal plane through the atomic centre of the constituent atoms, characteristic of a π-interaction. As evidenced above there is also another strong bonding interaction present between the 3p-orbital of the central Aluminium and the 3p-orbital of the terminal Chlorine. There is an analogous case where the Aluminium overlaps with the 4p-orbital of terminal Bromine. The combination of the two interactions dominate the bonding characteristics of the Molecular Orbital, yielding its overall bonding character, however, there are still a number of weaker through-space interactions must be considered. Firstly, there is a very weak through-space bonding interaction between the 3p-orbitals of terminal Chlorine and the 4p-orbitals of terminal Bromine, however, it occurs over a long distance and is non-directional hence its contribution to the overall stability of the Molecular Orbitals is negligible. This interaction may occur across either the top or bottom face of the molecule as shown above. Up to this point the Molecular Orbital has been observed to have entirely bonding characteristics but it is important to note that there is a degree of anti-bonding character in this Molecular Orbital. There is a weak out-of-phase (anti-bonding) through-space interaction between the 3p-orbitals of terminal Chlorine at the left of the molecule. The strength of this interaction is greater than the through-space bonding interactions discussed above but still weak in comparison to the strong π-interactions discussed first. It's increased strength compared to the through-space bonding interactions can simply be explained by the closer proximity of the interacting orbitals as the interaction is still non-directional. There is an analogous interaction between the 4p-orbitals of terminal Bromine to the right of the molecule as shown. The 4p-orbitals of Bromine have a smaller contribution to the Molecular Orbital than the 3p-orbitals of Chlorine, due to the increased energy gap between them and the final Molecular Orbital, and therefore this analogous anti-bonding interaction is somewhat weaker. The final point of note in determining the bonding characteristics of the Molecular Orbital is the presence of nodes at the atomic centres of the terminal halogens. These nodes are present at the atomic centre and therefore have little contribution to the energy of the Molecular Orbital, however, the nodal plane described previously can be described as internuclear and therefore exhibits a larger contribution to the energy of the Molecular Orbital. Despite these comparatively weak anti-bonding interactions, it may be concluded that this Molecular Orbital is of primarily bonding character although not quite to the same degree as Molecular Orbital 37.

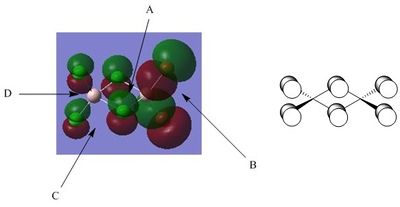
Molecular Orbital Fourty-Three

A - This demonstrates a relatively weak through-space bonding interaction between the 3p-orbital of the bridging Chlorine atom and the 3p-orbital of the terminal Chlorine atom. This interaction has a weak stabilising effect as it is non-directional and occurs over a relatively large distance, however, it still contributes to the bonding nature of the Molecular Orbital.

B - It is important to note here that the electron density centred on terminal Bromine (4p-orbital) is far more diffuse than the electron density centred on terminal Chlorine (3p-orbital) due to the increased size of Bromine and the high electronegativity of Chlorine. This is important in the analysis of other interactions as discussed below.

C - There is a large area of electron density here due to the relatively efficient σ-overlap of the constituent 4p Atomic Orbitals of terminal Bromine. This is therefore a strongly bonding interaction and acts to stabilise the Molecular Orbital significantly. It is important to note here that the Aluminium centre apparently has no Atomic Orbital contribution to this Molecular Orbital as a contribution from the Aluminium 3s-orbital would encompass the Aluminium centre within the region of high electron density under discussion and a 3p-orbital contribution would give rise to the characteristic change of phase in the central region of the Molecular Orbital.

D - There is a relatively weak in-phase (bonding) π-interaction between the 3p-orbitals of the bridging Chlorines across the central bridging region of the Molecular Orbital. This interaction is π-type as opposed to σ-type and therefore has a relatively small contribution to the stability of the molecule, however, it still contributes to the overall bonding character of the Molecular Orbital. It is also worthy of note here that the 3p-orbital electron clouds are somewhat distorted such that the distribution of electron density in this region is unsymmetrical. This distortion increases orbital alignment in both this bonding interaction and the bonding interaction in A and hence further stabilises the Molecular Orbital.

E - This simply highlights the presence of distinctive nodal planes at the atomic centre where the contributing Atomic Orbitals are p-type. Here we have identified specifically the nodal plane across the central bridging region, however, there are further nodes located on the atomic centres of the terminal halogens.

F - This interaction is very similar to that discussed in C, however, the contributing terminal halides in this case are both Chlorine. The constituent orbitals are analogous to C and therefore will not be discussed in detail. The important point of note is the increased diffusivity of the electron cloud in C. Although the Aluminium does not contribute directly to this Molecular Orbital, it is still highly polarising and therefore the introduction of more polarisable terminal Bromine as opposed to the less polarisable terminal Chlorine increases the diffusivity of the electron cloud in this region. In addition to the previous comparison to the diffuse electron cloud C, it is important to clarify that this region also displays strong bonding characteristics and therefore stabilises the Molecular Orbital

There a two major bonding interactions in the Molecular Orbital visualised above, both of which are of moderate strength. At the left side of the molecule there is a directional bonding interaction between the 3p-orbitals of the terminal Chlorines. It might have been predicted that such a directional in-phase interaction would be strong, however, its strength is reduced somewhat by the relatively large separation between the terminal Chlorines. In addition to this there is a π-interaction of the bridging Chlorine 3p-orbitals. Again this bonding interaction would be of moderate strength although probably slightly weaker than that discussed previously due to the decreased efficiency of orbital overlap. There are number of smaller contributions to the overall bonding characteristics of this Molecular Orbital, bonding and anti-bonding, mainly centred around the 3p-orbitals of the bridging Chlorines. We shall take one bridging Chlorine as an example; it exhibits two through-space interactions with the p-orbitals of the terminal halogens, one bonding, one anti-bonding. Firstly, there is a weak through-space in-phase (bonding) interaction between the 3p-orbital of the bridging Chlorine and the 3p-orbital of the terminal Chlorine. Secondly, there is a slightly stronger, although still comparatively weak, through-space out-of-phase (anti-bonding) interaction between the 3p-orbital of bridging Chlorine and the 4p-orbital of the terminal Bromine. These interactions are mirrored on the other side of the molecule and have an overall anti-bonding effect. Despite this, the Molecular Orbital can be concluded to have overall bonding character, although it is somewhat reduced compared to the strong bonding nature of Molecular Orbital 37.

Molecular Orbital Fourty-Six

A - There is an in-phase π-interaction possible here between the 3p-orbitals of the bridging Chlorines, which acts to stabilise the Molecular Orbital to some degree. The interaction is π-type as opposed to σ-type and is therefore relative weak, however, it has a fairly high degree of directionality and therefore contributes significantly.

B - There is an out-of-phase interaction between the 4p-orbitals of the terminal Bromine atoms which contributes to the anti-bonding nature of the Molecular Orbital. The contribution of the 3p-orbitals is easily distinguished by the characteristic nodal plane at the atomic centre. The electron cloud in this region is relatively diffuse due to a combination of the highly polarising Aluminium centres and the comparatively high polarisability of the terminal Bromines. This acts to attract electron density towards the Aluminium centre despite the fact that there is no direct Atomic Orbital contribution from the Aluminium itself.

C - This through-space bonding interaction occurs between the 3p-orbitals of the terminal and bridging Chlorines, however, it is very weak due to the low directionality of the orbital overlap. Intuitively it may be predicted that these orbitals interact in a π fashion but in reality it is observed that the constituent 3p-orbitals are somewhat distorted such that the interaction in non-directional and weak. This weak bonding interaction is negligible in comparison to the strong anti-bonding interactions discussed in B and D and therefore does little to counteract the overall anti-bonding nature of this Molecular Orbital. It is important to note that an analogous bonding interaction exists between the 4p-orbitals of terminal bromine and the 3p-orbitals of the bridging Chlorines, however, the efficiency of orbital overlap in this case is even lower and this combined with the non-directionality and large separation result in it being a weak stabilising interaction.

D - Interaction D is extremely similar to interaction B, however, it is now an out-of-phase (anti-bonding) interaction between the 3p-orbitals of the terminal Chlorine atoms which is observed. The contributing Atomic Orbitals are analogous to those of B and therefore we shall not discuss this in detail apart from to say that this is a significant anti-bonding contribution. It must be compared to the electron cloud probed in B and it is immediately apparent that this electron cloud has a lower diffusivity than in B, primarily due to the increased electronegativity of Chlorine in comparison to Bromine.

Overall it may be concluded that this Molecular Orbital is of predominantly anti-bonding character, with the bonding characteristics of the orbital dominated by the strongly anti-bonding out-of-phase interactions described in B and D. Despite this, there are still some bonding interactions within the Molecular Orbital, however, they are simply through-space interactions of comparatively low directionality and therefore they are weak in comparison to the anti-bonding contributions. The majority of the anti-bonding interactions are centred around the central Aluminium atoms.

Molecular Orbital Fourty-Nine

Interaction A - This refers to the out-of-phase π-interaction of the 3p-orbitals of Chlorine - there is no contribution from the Aluminium centre. The interaction is highly localised on Chlorine due to the fact that it is energetically favourable to maximise the separation between the out-of-phase interacting orbitals so as to minimise the anti-bonding interaction. This section of the Molecular Orbital is therefore completely anti-bonding in character.

Interaction B - There is a through-space out-of-phase (anti-bonding) interaction between the 3p-orbitals of the bridging Chlorines. This interaction is in many ways analogous to that described above resulting in the electron density being highly localised on Chlorine in this part of the Molecular Orbital in order to reduce the magnitude of this anti-bonding interaction. This interaction would again be entirely anti-bonding in nature.

As discussed above, both of the interactions identified are entirely anti-bonding in nature with no immediately obvious bonding interactions possible. The two interactions described are both out-of-phase p-orbital interactions between the respective pairs of Chlorine atoms, however, it is important to note here that there is a weaker through-space anti-bonding interaction possible between points A and B. The degree of orbital overlap is much lower in this interaction and therefore it is much weaker, however, it still serves to further raise the energy of the Molecular Orbital.

Conclusion

The project completed in the second half of this report determined the energies, vibrational modes and Molecular Orbitals of the six isomers of Al₂Cl₄Br₂. The optimisation, frequency and population analysis were all performed by applying knowledge from the first section of this report, utilising the 6-31G(d,p) basis set on Aluminium and Chlorine whilst utilising a LanL2DZ pseudo-potential on Bromine. The relative energy of the isomeric species were analysed and rationalised with success. A large number of stabilising effects were discussed in regard to electron deficient group 13 species, ranging from π-stabilisation in monomeric Boron species to the dimeric stabilisation of Aluminium species. The effect of varying the position of halides between terminal and bridging was rationalised with regards to the comparative stability of the isomers and their vibrational spectra. The final stage of the project was population analysis, yielding the Molecular Orbitals presented above. A number of these orbitals were analysed specifically, ranging from highly bonding to highly anti-bonding, rationalising their relative energies and bonding characteristics. There are many opportunities to extend the analysis in this project, for example investigating trimeric species, the effect of not using pseudo-potentials of Bromine or the comparative stability of Boron monomers (as mentioned previously).

References

1 - V.Gomez, M. Reves, S.Alvarez, B. Cordero, J. Echeverria, E. Cremades, F. Barragan and A.E. Platero-Prats, Dalton Trans. (21), 2008,2832-2838

2 - P. Atkins, T. Overton, J. Rourke,  M. Weller, F. Armstrong, Inorganic Chemistry, OUP Oxford, 2010 

3 - P. Atkins, J. de Paula,  Physical Chemistry, OUP Oxford, 2010

4 - http://www.gaussian.com/ (accessed 12/12/2014)

5 - T. L. Cottrell, The Strengths of Chemical Bonds, 2d ed., Butterworth, London, 1958

6 - B. deB. Darwent, National Standard Reference Data Series, National Bureau of Standards, 31, Washington, 1970

7 - S. W. Benson, J. Chem. Educ., 42:502, 1965

8 - J. A. Kerr, Chem. Rev., 66:465, 1966

9 - http://web.chem.ucsb.edu/~zakariangroup/11---bonddissociationenergy.pdf (accessed 11/12/2014)

10 - M. Chaplin, Water's Hydrogen Bond Strength, http://arxiv.org/ftp/arxiv/papers/0706/0706.1355.pdf (accessed 14/12/2014)