Rep:Mod:complab97

NH₃ Molecule

A model of this molecule was made using the program Gaussview. All 3 bond angles were set to 1.3 Angstrom and the point group set to C_3V. The structure of this molecule is an rough estimate, and will be optimised to find the lowest energy structure.

The structure is optimised by Gaussian using a plot of potential energy vs. the positions of the hydrogen atoms relative to to the central nitrogen atom, starting from the estimated structure that has been made. The positions of the hydrogen atoms are changed a small distance in both directions, and compared to gradient of the line (the 1st derivative). If the gradient is now smaller, Gaussian continues to calculate the gradient for small movements in this direction. Using this method, Gaussian attempts to find the positions of nuclei, where the gradient is as close to zero as possible - which is the lowest energy (equilibrium) position of the molecule.

Jmol image of optimised NH3 molecule

The following parameters were used in the Gaussian optimisation:

Calculation method: B3LYP

Basis set: 6-31G(d,p) - medium level of accuracy

Type of calculation to do: OPTF (optimise and frequency analysis) - this is used to determine the optimum (lowest energy) positions of the nuclei

Further commands used: pop=(full,nbo) - pop=NBO runs a population analysis to calculate the atomic charges; pop=full calculates all of the MOs

Optimisation Results

Final energy: E(RB3LYP): -56.44397188 au

RMS gradient: 0.05399560 au

Point group: C_3V

N-H bond length: 1.01798 angstrom

H-N-H bond angle: 105.741 degrees

Gaussian Calculations

         Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000072     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES

The following graph (below right) represents the change in potential energy as Gaussian optimises the structure of the molecule. As the basis set 6-31G(d,p) only has medium accuracy, there are relatively few steps before the optimised structure is reached.

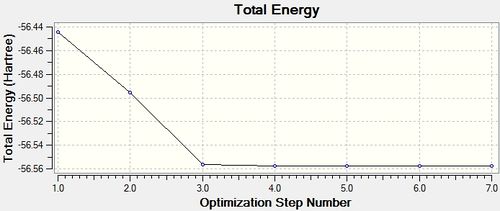
Vibrational Analysis

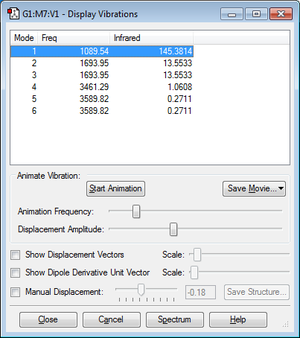
6 vibrational modes are expected from the 3N-6 rule

Modes 2 & 3 are degenerate; so are modes 5 & 6

The "bending" vibrations are modes 1, 2, and 3

The "stretching" vibrations are modes 4, 5, and 6

Mode 4 is the highly symmetric vibrational mode

Mode 1 is the "umbrella" vibrational mode

4 bands would be seen in an experimental spectrum of gaseous ammonia - although there are 6 vibrational modes, due to the degenerate modes, vibrations only occur at 4 different frequency bands

Charge Distribution

Charge of N: -1.125 Charge of H: +0.375

These charges are expected, as nitrogen is more electronegative than hydrogen

N₂ Molecule

N₂ optimisation file

Optimisation Results

Final energy: E(RB3LYP): -109.52359111 au

RMS gradient: 0.02473091 au

Point group: D*H

N-N bond length: 1.10550 angstrom

Gaussian Calculations

   Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000000     0.001200     YES

Vibrational Modes

There is one vibrational mode for N₂, frequency = 2457.33 cm^-1

Jmol image of optimised N2 molecule

H₂ Molecule

H₂ optimisation file

Optimisation Results

Final energy: E(RB3LYP): -1.17853936 au

RMS gradient: 0.00000017 au

Point group: D*H

H-H bond length: 0.74279 angstrom

Gaussian Calculations

   Item               Value     Threshold  Converged?
 Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000001     0.001200     YES

Vibrational Modes

There is one vibrational mode for H₂, frequency = 4465.68 cm^-1

Jmol image of optimised H2 molecule

Energies of N₂ + 3H₂ -> 2NH₃

Units(a.u.)

E(NH3)= -56.44397188

2*E(NH3)= -112.88794376

E(N2)= -109.52359111

E(H2)= -1.17853936

3*E(H2)= -3.53561808

ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= 0.17126543 au

ΔE = 449.66 kJ/mol^-1

CN^- Analysis

CN^- optimisation file

Jmol image of optimised CN- molecule

Optimisation Results

Final energy: E(RB3LYP): -92.82453153 au

RMS gradient: 0.00000704 au

Point group: C*V

C-N bond length: 1.18409 angstrom

Gaussian Calculations

         Item               Value     Threshold  Converged?
 Maximum Force            0.000012     0.000450     YES
 RMS     Force            0.000012     0.000300     YES
 Maximum Displacement     0.000005     0.001800     YES
 RMS     Displacement     0.000008     0.001200     YES

Charge Distribution

The carbon atom has a charge of -0.246; the nitrogen atom has a charge of -0.754. This is expected, nitrogen is more electronegative than carbon so will have a more negative charge, and the total charge adds up to -1.

Vibrational Analysis

This molecule has one vibrational mode, a symmetrical bond stretch at 2139.19 cm^-1

Molecular Orbitals

These images show the LUMO+1, the LUMO, the HOMO, and the 3 orbitals next lowest in energy of the CN^- ion. The grey atom is carbon; the blue is nitrogen.