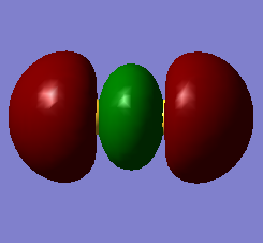Rep:Mod:compchemjh6415
NH3 Molecule
Bond Distances and Angles
N-H bond distance = 1.01798 Å
H-N-H bond angle = 105.741°
Summary Information
Molecule name: NH3
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy E(RB3LYP): -56.55776873 au
RMS gradient: 0.00000485 au
Point group: C3V
Item Table
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
Image of Structure
NH3 Molecule |
The optimisation file for the molecule is linked to File:JHUMMELL NH3 OPTF POP.LOG
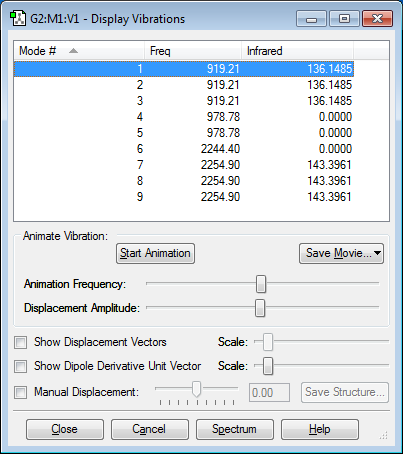
Vibrations of the Molecule
It can be seen that there are 6 vibrational modes. There are no negative frequencies.
Questions
How many modes do you expect from the 3N-6 rule? - You would expect 6 modes (3*4-6).
Which modes are degenerate? - Modes 2 and 3, and modes 5 and 6 are degenerate as they have the same frequencies, as seen in the table.
Which modes are "bending" vibrations and which are "bond stretch" vibrations? - Modes 1,2 and 3 are bending vibrations and modes 4,5 and 6 are stretching vibrations.
Which mode is highly symmetric? - Mode 4 is highly symmetric.
One mode is known as the "umbrella" mode, which one is this? - Mode 1 is the "umbrella" mode.
How many bands would you expect to see in an experimental spectrum of gaseous ammonia? - You would expect to see 4 bands since modes 2 and 3, and modes 5 and 6 are degenerate so only produce one band.
Charges on the Molecule
Charge on N atom = -1.125
Charge on H atom = +0.375
You would expect nitrogen to have a negative charge and hydrogen to have a positive charge as nitrogen is much more electronegative than hydrogen.
N2 Molecule
Bond Distances and Angles
N-N bond distance = 1.10550 Å
N-N bond angle = 180°
Summary Information
Molecule name: N2
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy E(RB3LYP): -109.52412868 au
RMS gradient: 0.00000060 au
Point group: D∞h
Item Table
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
Image of Structure
N2 Molecule |
The optimisation file for the molecule is linked to File:JHUMMELL N2 OPTF POP.LOG
Vibrations of the Molecule
It can be seen that there is 1 stretching mode at frequency 2457.33. There are no negative frequencies. You would expect there to be 1 vibrational mode according to the 3N-5 rule.
Charges on the Molecule
There is no charge on the atoms as both atoms are the same element so there's no difference in electronegativity.
H2 Molecule
Bond Distances and Angles
H-H bond distance = 0.74279 Å
H-H bond angle = 180°
Summary Information
Molecule name: H2
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy E(RB3LYP): -1.17853936 au
RMS gradient: 0.00000017 au
Point group: D∞h
Item Table
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
Image of Structure
H2 Molecule |
The optimisation file for the molecule is linked to File:JHUMMELL H2 OPTF POP.LOG
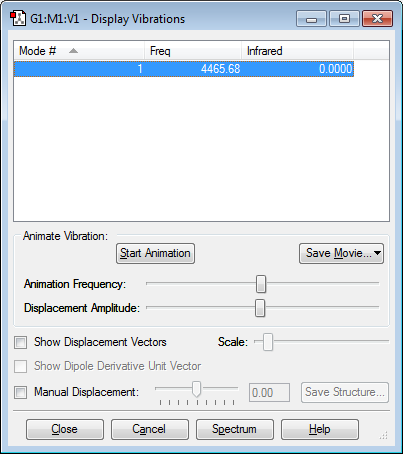
Vibrations of the Molecule
It can be seen that there is 1 stretching mode at frequency 4465.68. There are no negative frequencies. You would expect there to be 1 vibrational mode according to the 3N-5 rule.
Charges on the Molecule
There is no charge on the atoms as both atoms are the same element so there's no difference in electronegativity.
Haber-Bosch Reaction Energies
E(NH3)= -56.55776873 au
2*E(NH3)= -113.1155375 au
E(N2)= -109.52412868 au
E(H2)= -1.17853936 au
3*E(H2)= -3.53561808 au
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579074 au
Energy for converting hydrogen and nitrogen gas into ammonia gas (ΔEx2625.5) = -146.48 kJ/mol.
The ammonia product is more stable as it is lower in energy than the gaseous reactants, since the reaction is exothermic.
Project Molecule: S2 Molecule
Bond Distances and Angles
S-S bond distance = 1.92943 Å
S-S bond angle = 180°
Summary Information
Molecule name: S2
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy E(RB3LYP): -796.32599779 au
RMS gradient: 0.00000372 au
Point group: D∞h
Item Table
Item Value Threshold Converged?
Maximum Force 0.000006 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.000011 0.001800 YES RMS Displacement 0.000016 0.001200 YES
Image of Structure
S2 Molecule |
The optimisation file for the molecule is linked to File:JHUMMELL S2 OPTF POP.LOG
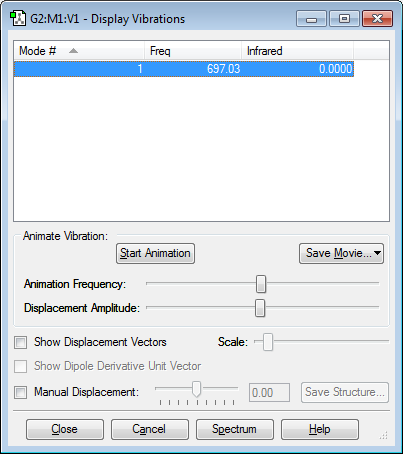
Vibrations of the Molecule
It can be seen that there is 1 stretching mode at frequency 697.03. There are no negative frequencies. You would expect there to be 1 vibrational mode according to the 3N-5 rule.
Charges on the Molecule
There is no charge on the atoms as both atoms are the same element so there's no difference in electronegativity.
Molecular Orbitals
This molecular orbital is a combination of the 3s valence atomic orbitals. The molecular orbital is a sigma bonding orbital and is occupied. It is lowest in energy (-0.83212 au) out of the molecular orbitals formed from atomic orbitals with quantum number 3. Occupation of this molecular orbital forms a sigma bond between the sulfur atoms.
This molecular orbital is a combination of the 3p valence atomic orbitals along the bond. The molecular orbital is a sigma bonding orbital and is occupied. It is lowest in energy (-0.39516 au) out of the molecular orbitals formed from the 3p atomic orbitals, but higher than the sigma molecular orbital formed from the 3s atomic orbitals. Occupation of this molecular orbital forms a sigma bond between the sulfur atoms.
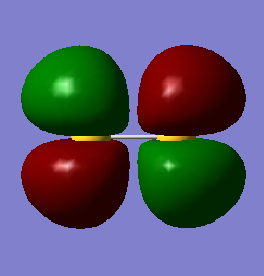
This molecular orbital is a combination of the 3p valence atomic orbitals perpendicular to the bond. The molecular orbital is a pi bonding orbital and is occupied. Each sulfur atom has two 3p orbitals that are perpendicular to the bond so there are two of these molecular orbitals. It is lower in energy (-0.36284 au) than the antibonding orbitals but is higher in energy than the sigma bonding orbitals. Occupation of this molecular orbital forms a pi bond between the sulfur atoms.
This molecular orbital is a combination of the 3p valence atomic orbitals perpendicular to the bond. The molecular orbital is a pi antibonding orbital and is occupied by a single electron, so is a SOMO. Each sulfur atom has two 3p orbitals that are perpendicular to the bond so there are two of these molecular orbitals. The occupation of this molecular orbital breaks the pi bond between the sulfur atoms. S2 is in the triplet state.
This molecular orbital is a combination of the 3p valence atomic orbitals along the bond. The molecular orbital is a sigma antibonding orbital and is unoccupied. It is the highest in energy (-0.01305 au) out of the molecular orbitals formed from atomic orbitals with quantum number 3 and is the LUMO. It is unoccupied so will not have an effect on bonding.
Extra Calculation: SiH4 Molecule
Bond Distances and Angles
Si-H bond distance = 1.48485 Å
H-Si-H bond angle = 109.471°
Summary Information
Molecule name: SiH4
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy E(RB3LYP): -291.88802760 au
RMS gradient: 0.00000002 au
Point group: Td
Item Table
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
Image of Structure
SiH4 Molecule |
The optimisation file for the molecule is linked to File:JHUMMELL SIH4 OPTF POP.LOG
Vibrations of the Molecule
It can be seen that there are 9 vibrational modes. This is expected from the 3N-6 rule. There are no negative frequencies. Modes 1-5 are bending vibrations and modes 6-9 are stretching vibrations.
Charges on the Molecule
Charge on Si atom = +0.629
Charge on H atom = -0.157
This is expected as hydrogen is more electronegative than silicon.