Rep:Mod:com7

Gareth Naylor

Introduction: Module 1: Modelling using molecular mechanics

Molecular modelling is a very useful technique in predicting the properties of a molecule and the reactions which it undergoes. In this module, this technique is first used to predict the energy of two products of a reaction and therefore predict whether the reaction proceeds with thermodynamic or kinetic control. The energy of many different conformations can also be analysed in order to calculate the lowest energy conformation for pairs of molecules. In the fourth exercise, molecular modelling is used to investigate molecular orbitals in a molecule. This makes it possible to find the most likely destination of attack in a molecule. Finally a pair of isomers, chosen from the literature, can be investigated in terms of their spectroscopic properties. This tests the accuracy of the computations and the literature and makes it possible to distinguish between two isomers using spectroscopic techniques.

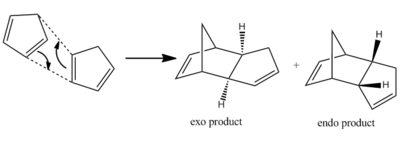
The Hydrogenation of the cyclopentadiene dimer

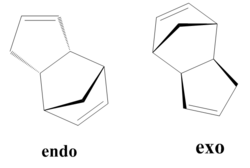
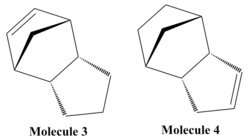
It is possible for two cyclopentadiene dimers to perform a Diels-Alder cycloaddition reaction in order to form one of two isomers, either the endo or the exo isomer. This reaction is given in figure 1. If these products are hydrogenated they can form either molecule 3 or molecule 4 shown in figure 2. It is also possible to form a tetrahydro derivative, however this only occurs after prolonged hydrogenation.

Fig 1: mechanism for the formation of cyclopentadiene dimer

Table 1: breakdown of energies for endo and exo dimers

Energy/kcal mol-1	endo	exo
Stretch	1.25	1.29
Bend	20.85	20.59
Stretch-bend	-0.83	-0.84
Torsion	9.51	7.65
Non-1,4 VDW	-1.52	-1.42
1,4 VDW	4.31	4.23
Dipole/Dipole	0.45	0.38
Total Energy	34.00	31.88

Table 1 compares the properties of the endo and exo forms, calculated using the MM2 minimization of energy function found on ChemBio3D. The total energy of the molecules is an indication of the steric strain exerted on them, therefore the molecule with the greater steric strain will have a larger value of energy. In this case, the energy of the exo form is lower than the total energy of the endo form, however it is known that the endo product predominates. The difference in total energies can be explained by looking at the breakdown of the individual components. From this it can be seen that the major difference between the exo and endo forms lie in the torsion energy due to the different torsional strain of the rings in each case. In this reaction the kinetic product is formed. This can be explained from the fact that the kinetic product considers the stability of the transition state whilst the thermodynamic product considers the energy of the products.

Fig 2: Endo and Exo structures for cyclopentadiene dimer

In 1937, Alder and Stein stated that endo attack normally leads to a more stable transition state. This was known as the endo rule. This meant that endo attack will give the more stable product even if the other product is thermodynamically more stable.

The higher energy of the endo structure can be explained by the interaction of the bridged methyl group with the individual hydrogens attached to the two carbons at the stereocentre. On the other hand, in the exo isomer, the individual protons point away from any other atoms, and therefore no extra strain is experienced. This explains the higher torsional strain of the endo structure.

Fig 3: Structures for molecules 3 and 4

Table 2:breakdown of energies for molecules 13 and 14

Energy/kcal mol-1	Molecule 3	Molecule 4
Stretch	1.30	1.09
Bend	19.81	14.52
Stretch-bend	-0.84	-0.55
Torsion	10.82	12.51
Non-1,4 VDW	-1.20	-1.07
1,4 VDW	5.63	4.50
Dipole/Dipole	0.16	0.14
Total Energy	35.64	31.16

Hydrogenation of the Endo Dimer

The endo dimer can be hydrogenated to form two separate dihydro derivatives shown in figure 3. As with the above dimerisations, it is possible to calculate the total energy of these molecules from the sum of their individual component parts using an MM2 calculation. Table 2 shows that molecule 4 is lower in energy than molecule 3, meaning that hydrogenation of the norbornene double bond is favourable compared with hydrogenation of the cyclopentene ring. In this case, the major difference occurs due to the fact that the bend energy of molecule 3 is 5.39kcal/mol greater than the bend energy of molecule 4. This suggests that the hydroboration of the norbornene relieves the most steric strain.

Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD⁺ analogue)

Schultz et al reported in 1986 that addition of carbon nucleophiles to pyridinium salts can occur at both the 1,2- and the 1,4- position. They then applied this theory to piridoxazepinone, a derivative of proline. In this example a grignard reagent, MeMgI, was used as then source of the carbon nucleophile. A mechanism for this reaction, which gives absolute stereochemistry, is shown in figure 4. This was taken from a paper by Schultz et al.

Figure 4:mechanism for nucleophilic attack by an Me group on pyridinium salt

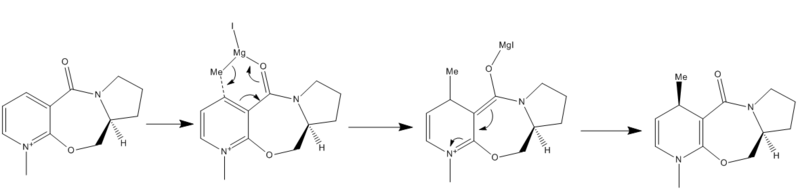
It was believed that coordination of the magnesium in the Grignard reagent to the amide oxygen, via the oxygen lone pair, resulted in the high regio- and stereoselection. The organic group was then transferred from the magnesium group to the ring leaving a magnesium enolate. It was also discovered that the seven membered ring in the reagent has very little conformational flexibility. In order to take the minimum energy of the reagent, it was necessary to build the molecule up by minimising the energies of several fragments of the molecule. The completed reagent was modelled using an MM2 calculation, the lowest energy conformation discovered had an energy of 35.67kcal/mol and a dihedral angle of 22.1 degrees. This value for the dihedral angle suggests that the carbonyl group is above the plane of the pyridine ring with respect to the cyclopentane ring. This conformation can be viewed by clicking this button . The breakdown of energies can be viewed in table 5. This low energy conformation matches the one described in the literature. The magnesium Grignard reagent was not included in the MM2 calculation due to the fact that the ChemBio3D program will not run an MM2 calculation when the magnesium is present. It is possible to vary the conformation of the molecule to obtain molecules with a higher total energy. Their conformations can be viewed by clicking on the following two buttons. The breakdown of the total energies of molecules 5b and 5c into their component parts is also shown in table 5.

Table 3: energies for 3 conformations of molecule 5

Energy/kcal mol-1	molecule 5	molecule 5b	molecule 5c
Stretch	1.20	1.83	1.32
Bend	7.37	14.28	8.45
Stretch-bend	0.085	0.15	0.13
Torsion	14.02	6.15	13.57
Non-1,4 VDW	-2.23	0.58	-1.66
1,4 VDW	16.22	16.81	15.94
Charge/Dipole	2.81	1.79	10.80
Dipole/Dipole	-3.81	3.93	-3.88
Total Energy	35.67	36.50	44.68

Table 5 shows no particular trends with regard to the increases in energy. The differences in each individual component can be explained by the changes in the conformation of each individual molecule.

Reaction of N-methyl Quinolinium Salt with Aniline

This example involves a similar reaction involves aniline performing a nucleophilic attack on a similar pyridinium ring to the one shown in the above example. In this case, a 1,4- addition is the only addition possible as both 2-positions are blocked by adjacent rings. The mechanism for this reaction is shown in figure 5.

Figure 5: mechanism for attack on PhNH² on pyridinium ring

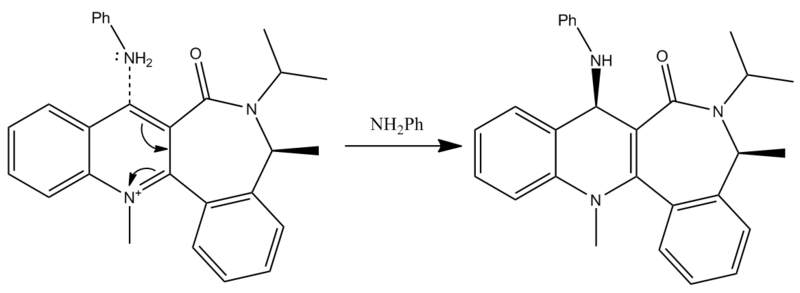
The lowest energy conformation of the reagent was found using the same method as above. This conformation can be viewed by clicking the following button. The energy of this molecule is 62.61kcal/mol whilst the dihedral angle is -19.81degrees. The stereocontrol in the product can be explained using the reactants. A similar reaction to the nucleophilic addition in the above example does not occur as the lone pairs of the oxygen and nitrogen will repel. The negative dihedral angle confirms the view that the oxygen and nitrogen atoms repel, as this angle means that the carbonyl oxygen is below the plane of the adjacent rings. The nitrogen atom in the product is shown to be above the plane of the ring, attacking the top face, confirming that the nitrogen and oxygen were kept as far apart as possible.

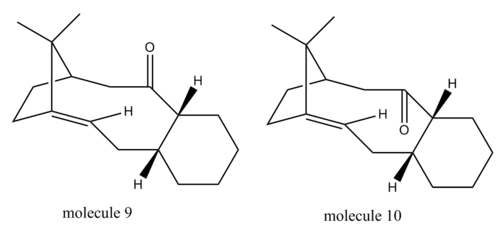
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

Figure 6:Two stereoisomers of taxol

Table 4:energies of two stereoisomers of taxol

Energy/kcal mol-1	Molecule 9	Molecule 10
Stretch	2.67	2.52
Bend	15.88	10.70
Stretch-bend	0.39	0.31
Torsion	18.28	19.73
Non-1,4 VDW	-1.17	-1.37
1,4 VDW	12.70	12.59
Dipole/Dipole	0.14	-0.18
Total Energy	48.91	44.30

Taxol is a very important drug in the treatment of cancer. It was proposed by Paquette that a key intermediate in the synthesis of Taxol could have its carbonyl group pointing either up or down. This is demonstrated in figure 6. It was proposed that one of the molecules could isomerise to the other molecule when left to stand, an example of atropisomerism. Atropisomerism can be explained as the effect that steric demand has on the rotation of a single bond in a specific molecule. This steric demand removes the ability of free rotation within that specific bond. The identity of the lower energy isomer was discovered using MM2 calculations. The results of these calculations can be viewed in table 4. The results show that molecule 10, with the carbonyl group pointing downwards, is the most stable isomer. The difference in energy between the two molecules is 4.61kcal/mol. In order to rationalise the difference in energies between the two molecules, it is necessary to analyse the conformations of the molecules. These can be viewed by clicking the following two buttons. From these conformations, it can be seen that molecule 9 is much more sterically hindered as the carbonyl group interacts unfavourably with the methyl group on the bridging carbon and the two hyrogens coming out of the plane. The down isomer is lower in energy as these unfavourable interactions are not present.

The energies of the molecules can also be calculated using the alternative MMFF94 calculation method, which is also found on the ChemBio3D program. Using this calculation method molecule 9 gave an energy of 70.53kcal/mol and a conformation of , whilst molecule 10 gave an energy of 60.54kcal/mol and a conformation of . These calculations show that the MMFF94 calculation technique gives a lower energy for molecule 10, much like the MM2 energy minimization technique. However, the energies given by the MMFF94 technique are higher than those given by the MM2 technique.

When the alkene group in this molecule is functionalised the reaction is abnormally slow. This is due to the alkene group in this molecule being a hyperstable alkene, which can occur in polycyclic ring systems with bridging carbons. The strain energy of hyperstable alkenes is lower than that of the parent alkane, therefore meaning that the alkene is more stable and will not functionalise as normal.

Modelling Using Semi-empirical Molecular Orbital Theory

So far in the exercises, only mechanical considerations have been taken into account in the energy calculations performed. However, in this exercise the effect of the electrons on reactivity will be taken into account, including how electrons influence bonds and certain spectroscopic properties. This represents a transition from a classical model to a quantum mechanical model.

Regioselective Addition of Dichlorocarbene

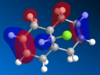
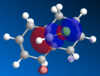
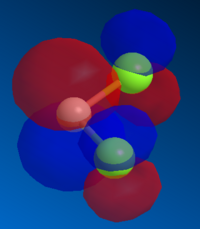
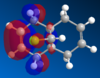
Molecule 12, , is an ideal example of how both classical and quantum mechanical treatment of a molecule can be performed. Molecule 12 possesses two double bonds which are able to react with an electrophile, the electron density at each of the double bonds will decide which the electrophile prefers to add too. In order to determine the electron density at each of the double bond an MM2 and a MOPAC/PM6 calculation were required. Firstly, the MM2 geometry optimization was performed on molecule 12 to give an energy of 17.89kcal/mol. Next a MOPAC/PM6 calculation was performed to give a representation of the electron density for each bond in the molecule. The HOMO was particularly focused on as it was presumed that this orbital was the most prone to electrophilic attack. This orbital and a selection of the other molecular orbitals is shown in table 5.

It is clear from the molecular orbital diagrams shown in table 5 that a bug is present in the ChemBio program. This is due to the fact that even though molecule 12 has a plane of symmetry, the electron density represented in these diagrams is not symmetrical. This meant it was necessary to repeat the calculations using the Gaussian interface. The resulting molecular orbitals, shown in table 6, have a completely symmetrical spread of electron density. From table 6 it is clear that the electronic representations produced using the Gaussian interface are much more reliable than those produced using the MOPAC/PM6 interface, as the electron distributions produced are symmetrical like the molecule in question. From analysing the HOMO it is clear that a large percentage of the electron density in the molecule is localised on the alkene group situated syn to the chlorine group. We are most interested in the HOMO as it will be the electrons of the HOMO which donate into the LUMO of the electrophile. Since we are analysing an electrophilic reaction, the alkene group with the greatest amount of electron density will be the preferred site of 'attack' for the electrophile. In comparison the alkene group anti- to the chlorine has very little electron density and so therefore this adduct will be the minor product whilst reaction with the alkene group syn to the chlorine will be the major product. It could be predicted that, due to the low amount of electron density on the anti adduct, the di-adduct product would also not be formed. The HOMO-1 orbital also produces a useful insight into the electron density of the syn alkene group. The anti-bonding C-Cl orbital interacts with the antibonding orbital of the syn alkene, in the process adding significant amounts of electron density to the exo side of the structure (as chlorine is very electronegative). This is therefore the reason behind the greater amounts of electron density at the syn alkene.

Table 5: molecular orbitals of molecule 12 obtained using the MOPAC interface

HOMO	LUMO	HOMO-1	LUMO+1

The molecular orbital representation of these molecules can also be used to predict the angle of 'attack' which the electrophile uses. The electrophile in question used in this case would be a dichlorocarbene. A molecular orbital representation of the LUMO orbital of this carbene is shown in figure 7. Figure 7 shows that the symmetries of the molecular orbital representations would match if the carbene attacked along the plane of the ring and perpendicular to the alkene double bond. It could then be predicted from the sterics of the molecule that the carbene would add to the bottom face.

Figure 7: carbene LUMO

Investigations were then centred on how the C-Cl bond effected the IR spectra for molecule 12 and its dihydo derivative, in which the anti- alkene bond was hydrogenated to a C-C single bond. Both molecules were computed using the Gaussian interface, with the key words opt and freq. The results of these computations, undertaken with a range of substituents are shown in table 7.

Table 6:Molecular orbitals of molecule 12 obtained using the Gaussian interface

HOMO	LUMO	HOMO-1	LUMO+1

Table 7: Comparison of stretching frequencies for different substituents

substituent-1	C=C stretching frequencies	C-Cl stretching frequency
-H (dialkene)	1739.0 & 1761.6	756.0
-H (monoalkene)	1758.1	764.97
-OH	1755.0 & 1761.9	754.3
-CN	1710.2 & 1762.2	756.62
-BH2	1660.0 & 1760.5	751.84
SiH3	1700.6 & 1761.3	753.9

In the cases in which there are two alkene stretching frequencies, the frequency which is lower will correspond to the anti frequency. These anti frequencies show the most variation between the five substituents tested. It would be expected that a more electron donating group would strengthen the anti- C=C bond and therefore increase the frequency of the stretch in the IR spectrum. From the data shown in table 7 it is possible to see that the anti stretching frequency is lowest for the -BH₂ substituent which is also the most electron withdrawing substituent analysed. This means that it will remove most electron density from the alkene double bond and weaken the IR stretching frequency the most. In contrast, -OH is the most electron donating substituent, because of its lone pairs. Therefore it will have the greatest IR stretching frequency.

Mini Project

Arizidines are three membered rings which contain two carbon atoms and a nitrogen atom. Much research has been done by Desai and Wulff into the diastereo- and enantio- selctivity of certain arizidines. The aim of this mini project is to investigate the two products of one reaction which yields arizidines in both the cis- and trans- forms and to try to prove what the literature concludes. This will specifically be done by investigating a range of properties using computational techniques and with the aid of the Gaussian interface. The reaction for the formation of the arizidine is shown in figure 7.

Fig 8: Reaction scheme for the formation of substituted Arizidines

It was first possible to use the MM2 minimise energy function to determine the minimum energy conformation. From this it was determined that the trans conformation was lower in energy than the cis conformation by 5.1kcal/mol. The optimised structures for these molecules can be seen by clicking the following buttons. A second optimised structure was taken using the Gaussian interface using the mpw1pw91 functional and the 6-31g basis set. These optimised structures were then used to compute other properties such as the NMR and IR, both of which were included in the literature.

¹³C NMR

The starting point in the mini project investigation is to compare the values obtained from the calculations on the Gaussian interface with those in the literature. The coordinates obtained from the optimisation were used to input into the new calculation. Again the mpw1pw91 functional and the 6-31g basis set were used, however on this occasion the key words NMR scrf(cpcm,solvent=chloroform) were used.

The NMR spectrum was obtained for both the cis and the trans isomer and the results compared with the literature.

The difference between the values from Gaussian and from the literature were also calculated. The results of these investigations are shown in table 8.

Table 8: Comparison of computed NMR values and literature NMR values for both cis and trans isomers.

trans			cis
Calculated shift (ppm)	Literature Shift (ppm)	Difference (ppm)	Calculated shift (ppm)	Literature Shift (ppm)	Difference (ppm)
172.0	168.1	3.9	163.8	167.5	3.7
142.6	143.2	0.6	138.7	142.3	3.6
141.5	142.8	1.3	136.9	142.1	5.21
139.0	137.3	1.7	134.8	134.4	0.4
129.5	132.0	2.5	130.6	131.5	0.9
127.2	128.7	1.5	129.4	130.8	1.4
126.5	128.4	1.9	128.3	128.8	0.5
125.8	128.2	2.4	127.3	128.5	1.2
125.7	127.9	2.2	126.0	127.7	2.5
125.5	127.8	2.3	-125.7	127.6	2.0
124.9	127.3	2.4	125.2	127.6	2.4
124.7	127.3	2.6	124.6	127.2	2.6
124.3	127.2	2.9	124.5	127.0	2.5
124.2	126.9	2.7	124.2	126.7	2.5
123.7	123.5	0.2	122.8	123.2	0.4
69.1	68.0	1.1	67.2	76.6	9.4
66.6	61.0	5.6	67.0	60.6	6.4
53.4	49.0	4.4	40.7	48.77	8.0
39.5	44.6	5.1	39.9	45.9	6.0
15.7	13.8	1.9	16.2	13.9	2.3

Table 8 shows a reasonably good correlation with the literature. In the benzene region, around 124-125ppm the correlations are particularly close, mostly around 2.5ppm out. As the values of chemical shift lowers, the correlation with literature decreases. However, this error can be assigned to the fact that these carbon atoms correspond to those in the ester group in the molecule, for which it has been shown that an error of up to 5ppm can occur.

Four peaks from the computational spectrum have been removed from this data due to the fact that the literature only reported 20 carbon peaks. This is mainly due to the fact that in an experimental NMR, the molecules are free to move around and so therefore some carbon atoms, especially those involved in a benzene ring structure, will become equivalent atoms in an experimental NMR. On the other hand, when a computational NMR is calculated, the molecule is frozen and so therefore the atoms in the molecule cannot move around and so it is impossible for carbon atoms to be equivalent.

There is not a notable difference between the literature values for the cis and trans isomer. The only major difference which occurs comes at 68.0ppm in the trans isomer and 76.6ppm in the cis isomer. This chemical shift corresponds to the carbon atom bonded to the nitrogen, however this carbon is not part of the ring. It is perfectly feasible that this is the carbon atom most affected by any change in geometry, from cis to trans, and so therefore it should be possible to distinguish between cis- and trans- isomers from this chemical shift. Unfortunately this difference is not particularly helpful as the greatest error occurs in this cis-isomer at this ppm. However the trans- isomer is quite accurate, so it is entirely possible that this chemical shift is the most important shift in differentiating between cis and trans isomers. It is also possible that the literature value for the cis isomer is not entirely accurate, maybe due to the fact that it was not completely isolated from the trans-isomer when the NMR was taken.

Infra-red Spectroscopy

It was also possible to compute an infra-red spectrum for both the cis- and trans- isomers. The values given from these tests can then be compared to the literature values much like the NMR investigations above. In this case the function for the calculation was changed to b31yp, whilst the basis set remained 6-31G(d,p). The key words used for these computations were opt and freq, this meant that these calculations could be run at the same time as the optimization calculations as the input file contains an opt key word in this case.

These infra-red investigations show varying results for the cis and trans isomers. For the cis- isomer it is possible to identify the C=O stretching frequency at 1799.1cm^-1,whilst it is also possible to assign the frequency at 1192.9cm^-1 to be C-H bends on the bromo-benzene ring. Peaks in the 1017.5cm^-1 area correspond to aromatic C-C stretches. Each peak corresponds to one of the ring stretches. The IR spectrum for the cis molecule is shown in figure 8.

Figure 9: infra-red spectrum for cis isomer

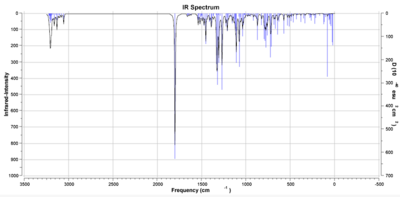
In the case of the trans isomer many of the peaks again match reasonably to those given in the literature. The peak at 3028.5cm^-1 corresponds to a stretch of the -CH₂ carbon-hydrogen bonds in the ethyl group. As for the cis- isomer, the peaks at 1838.8cm^-1 and 1017.5cm^-1 correspond to the carbonyl group and aromatic C=C bends. The peak at 1438.5cm^-1 is a peak which corresponds to C-H bending in the ethyl group. The infra-red spectrum for the trans isomer is shown in figure 9.

Figure 10: infra-red spectrum for trans isomer

Overall the infra-red analysis is not particularly helpful in differentiating between the molecules. Unfortunately the literature does not quote the same peaks for each isomer and so therefore it is difficult to compare them to the calculated values obtained. It is only really possible to differentiate between the molecules by looking at the carbonyl peak as these have a small difference in the literature. However, the peaks obtained from the computational methods are not accurate enough compared with the computational values to be able to make a reliable differentiation. Infra-red analysis is also not able to distinguish between cis and trans from basic peaks as they only correspond to to functional groups, therefore it is not very useful for this mini-project.

Optical Rotation

Values for optical rotation are also quoted in the literature, however due to the fact that the two molecules in question are stereoisomers and not optical isomers, it is not relevant to use this technique to distinguish between them. It is also an issue that it is not certain which optical isomer has been tested and which one has been quoted in the literature. This all meant that the values computed for optical isomers did not match the literature values. This is shown in table 9.

Table 9: comparison of the IR values from computations and literature for both the cis- and trans- isomer.

trans		cis
Calculated peak (cm-1)	Literature peak (cm-1)	Calculated peak (cm-1)	Literature peak (cm-1)
3028.5	3028	1799.1	1738
1838.8	1726	1192.9	1199
1438.5	1414	1017.5	1028
1330.6	1332	79.8	74
1127.5	1188
1017.4	1026

Table 10: comparison of computed optical rotation with literature values.

	trans	cis
Computed optical rotation	-26.0	-301.97
Reference optical rotation	-8.5	155.63

Conclusion

In conclusion, it was very difficult to distinguish between the two isomers from the spectroscopic techniques used in this investigation. There is a slight change between the NMR values which makes it possible to identify the isomers, however it is very difficult from IR and almost impossible to use the optical rotation values to distinguish. On the other hand, the NMR values fit those obtained from literature fairly well meaning that this was a reasonable molecule to choose.

Overall Conclusion

In conclusion, this project has proven that molecular mechanics is a very useful way of predicting the properties of molecules and reaction. This is particularly true for finding the lowest energy conformation and for comparing the molecular orbitals for molecules. Unfortunately in this case spectroscopic techniques did not prove successful in distinguishing between molecules, however the spectroscopic techniques did match with experimental data reasonably well. This means that this is certainly a technique that could be used in the future for confirming the identity of molecules.