Rep:Mod:coke3
Physcial Computing Lab
Cope Rearrengement
The first optimisation problem was looking at the cope rearrangement of 1,5-hexadiene. This is considered to be a [3,3]-sigmatropic shift rearrangement and both the products, reactants and transition state will be analysed in this section in order to determine the type of mechanisum this reaction proceeds by.
Reactant and Product Optimisation

The first optimisation was obtained for the "anti" (at the 4 carbon) conformation. This structure was cleaned and then re-checked to confirm that the structure was still of the same conformation. This was optimised to HF/3-21G level of theory; this is a low level of theory but obtains good results as an intial optimisation as results are obtained quickly. The energy obatined from this optimum structure was -231.69260236 a.u ( -608308.9 kJ/mol) and had the symmetry of C 2.
The next optimisation was of the "gauche" (at the 4 carbon) conformation. To save time the optimised structure from the previous optimisation was edited by changing the dihedral angle between the opposite ends of the chain from 180 o to 120 o, this created a already nearly optimised structure. This structure was the cleaned and double checked to make sure the "gauche" conformation had been kept. This too was optimised using the HF/3-21G level of theory. The energy obtained from this optimisation was -231.69266122 a.u. (-608309.1 kJ/mol) and had the point group of C 1 .
It was observed that the lowest energy conformation of the reactant molecule is used as a reference for the molecule and therefore dictates the calculated activation energies and enthapies. This therefore means that the lowest energy conformation is the state in which the moelcule is assumed to be in for latter calculations and is assumed that it is the state in which it spends most its time in. From the results above this is assumed to be the gauche conformer that has been calculated above. From latter discussion can be seen that this is the lowest energy conformer so subsequent optimisations were not required.
The two optimisations obtained are both the lowest energy confomers of the gauche and anti conformations (Appendix 1, http://www.ch.ic.ac.uk/wiki/index.php/Mod:phys3 ) and were given the labels "gauche3" and "anti1". When comparing the energies it is seen that although very similar the gauche is seen to have slightly lower in energy despite incurring more steric strain due to the low dihedral angle between the two terminal groups. This seems to contradict what would be expected if sterics was the dominant factor. However this difference occurs because with a chain molecule, having a certain amount of guache turns in the molecule actually stabilises the molecule due to the entropy that it induces within the molecule. To have a molecule that is completely anti is too structured so is entropically less favoured. It is also noted that due to the carbon either side of the carbon 4 bond only being sp 2 hybridised it is inducing less of a steric effect then if it were sp 3 hybridised.

The next optimisation was of the "anti2" conformation which had the C i point group. This agin was optimised to HF/3-21G level of theory and the point group was confirmed to be C i and the energy of the optimised molecule being -231.69253519a.u. (608308.8 kJ/mol). This is conparible to the "anti2" given the appendix 1 given above as they obtain the same number when rounded to the same significance therefore ensuring that the correct molecule has been optimised for the subsequent optimisations. This optimised molecule was then optimised to a higher degree of theory, B3LYP/6-31G* level, this gives a higher level of accuracy and can be considered to be a better approximation for real life. This obtained an energy of -234.55969657 a.u. (-615836.5 kJ/mol) and kept its C i to a loose agreement. This shows okay agreement with the stated energies although is 0.05a.u. higher in energy, at this high level of theory this small difference in energy could be down to very small changes in the geometry, as it is small it can be taken as being the same.It can be seen that the energy is lower, this would be becuse now the higher level of theory is constraining the molecule more so there has to be a higher level optimisation before the molecule is considered optimised. The geometry of the molecule from the optimisation at the HF/3-21G level of theory and at B3LYP/6-31G* level of theory are very similar showing that the higher of level theory is only "tweeking" the geomtry of the molecule. When looking at similar bond length is is seen that the double bond is lengthed in the second optimisation, although weakening the bond this effect reduces steric effects. The bond length increases from 1.316 Å to 1.338 Å after the second optimisation. Most of the other bond lengths are about the same (±0.002Å)and the dihedral angles around the 4 carbon is approximatly the same (±0.2o) although it should be noted that to 4 dp the second optimisation was 180.0000 o showing its tendency for the two groups to keep the symmetry of te moleule to a high degree.
Next a frequency calculation was performed on the optimisation molecule to the B3LYP/6-31G* level of theory. The frequency calculation was optimised to the same level. The reasoning for the frequency analysis is to include additional terms to the energies quoted so that they may be compared to theose stated from experimental data. By undertaking a frequency analysis it can also be confirmed that the molecule optimised is the real minima as it will have all real positive geometries if this is correct. After the frequency calculation was done it was seen that all frequencies were real and positive so it was confirmed that a minima had been found. From the addition calculations that the frequency analysis does the following data was also collected about the moelcule;
Sum of electronic and zero-point Energies= -234.416252 a.u.
Sum of electronic and thermal Energies= -234.408952 a.u.
Sum of electronic and thermal Enthalpies= -234.408008 a.u.
Sum of electronic and thermal Free Energies= -234.447895 a.u.
The "sum of electronic and zero-point energies"is the potential energy at 0 K including the zero-point vibrational energy (E = Eelec + Zero-Point E), the "sum of electronic and thermal Energies" is the energy at 298.15 K and 1 atm of pressure which includes contributions from the translational, rotational, and vibrational energy modes at this temperature (E = E + Evib + Erot + Etrans), the third contains an additional correction for RT (H = E + RT) which is particularly important when looking at dissociation reactions, and the last includes the entropic contribution to the free energy (G = H - TS). Each of these energies correspondes to a different enviroment so should be only used as a comparison to the right enviroment. It is important to make sure that the correct energy/enthalpy term has been selected to compare to the experimental values.
Transition States
The next set of optimisations were carried out to determine the transition state for the reaction stated above. This was doen by using 3 different methods each of which will be disscused as the optimisation is carried out. The first optimisation was that of the fragments of the transition state, which were decided to be the allyl fragment (CH2CHCH2). This was optimised using the HF/3-21G level of theory.
Chair
For this optimisation the optimised fragment was duplicated onto a new screen twice and these two fragments orientated so that it was 2.2Å from each of the reactive terminal ends. This was considered the intial "guess" for the transition state as it has a similar form to the proposed transition state. The transition state was then optimised manually using two differeent techniques. This is more difficult then a standard optimisation where a minima is located as the system needs to know where the negative direction of curvature is. The first method for this optimisation consists of an intial guess that needs to be close the the actual transition state. If the "guess" is not close enough to the actual transition state then the curviture of the potential surface may be vastly different from that needed by the transition state. The optimisation was then calculated using an optimisation+frequency job type, with the optimisation to a transition state (Berny). This is a method that uses the Berny algorithm. The Berny algorithm uses the forces acting on the atoms of the structure together with the Hessian matrix to predict energetically more favorable structures and thus optimize the molecular structure towards the next local minimum on the potential energy surface, in this case a transition state. It was also opted that the force constant should be calculated once with addition keywords, Opt=NoEigen which stops the calculation crashing if there are more then one imaginary frequency which can occur if the "guess" optimised is not close enough to the actual transtion state. This calculation was submitted and the results obtained. It was seen that the frequency output obatined consited of all poisitve real numbers par one vibrational frequency which realted to the actual reaction that we are investigating, the cope re-arrengment. This vibration was seen at -818.00 cm -1with an intensity of 5.87.
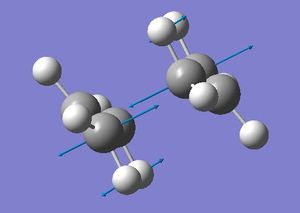
This negative (imaginary) frequency indicated corresponds to the vibration that is the same motion as the reaction itself. The mathematical reasoning behind the imaginary come from the mode of the vibration. As this vibration results in the reaction occuring and the transition state moving away from this state and moving towards the reactants/products, and therefore has no restoring force. Due to not having this restoring force the vibration is considered one way. When lookig at the force constant which is the first derivative of the gradient, the gradient is sloping down when moving along the reaction coordinate, so the force constant is negative for this mode of vibration. The frequency calculation involves the square root of the force constant so therefore creating an imaginary frequency for this vibration. (1)
The second type of optimisation can be done by freezing the coordinates of the transition points (ie the reactive ends) and allowing the rest of the molecule to optimise first. Once this optimisation has been carried out a second optimisation can be carried out which the reaction points are un-frozen and it optimises the reaction points , and a transtion state can be found. The main advantage of this is that the whole Hessian matrix (the square matrix of second-order partial derivatives of a function = it describes the local curvature of a function of many variables) may not have to calculated as a differential along the reaction coordinate may provide enough information to reach the transition state.
The guess structure was agian copied into a new screen and then using the Redundant Coordinate Editor the two reaction ends were frozen to 2.2 Å (the proposed distance in the transition state)and an optimisation was carreid out on the rest of the moelcue.After this intial optimisation it was seen that the transtion state was similar to that obtained in the previous method.The "frozen" bonds were then "unfrozen" and then a transition state optimistaion was undertaken but not having to calculate the force constant (unlike in the previous method). The vibrations were then observed as all being positive par one vibration similar to above but this vibration was seen at -817.76 -1 with an intensity of 5.85. This vibration also related to the cope rearrengement and had the same mode as the vibration pictured above.
The two transition states optimisations were then compared to see the benifits of both methods. It is seen that both methods produce the same transition state. The reactive ends were the same lengths to 3dp giving them to be 2.020 Å and the electronic energies were the same to 6 dp being -231.619 a.u. . When looking at the geometry of the molecule as expected they are both the same with the dihedral angle over the terminal ends being 54 o and the bond angle for over the termial ends being 101 o for all termials for both moleucles. The thermochemistry for the moelcule is given below;
Sum of electronic and zero-point Energies= -231.466699 a.u.
Sum of electronic and thermal Energies= -231.461339 a.u.
Sum of electronic and thermal Enthalpies= -231.460395 a.u.
Sum of electronic and thermal Free Energies= -231.495204 a.u.
Therefore both produce the same output when approched from the correct intial "guess" geometry.
Boat
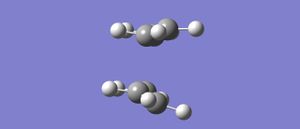

To Optimising the boat conformation a different method was used; the QST2 method. With this method the reactants and products were specified and then the transisiton state was obtained by working through the potential energy surface through them. Intially the optimised product C i from before was copied into two different panels, these pannels represented the series of the reaction ie products and reactants. The same molecule was able to be used twice due to the symmetry of the reaction- the forwards reaction and backwards reaction are the same. The numering of the atoms in the molecule were then changed so that the numbering changed from the reactants to the products and kept the continuity of the reaction. After this the an optimisation+frequency analysis was submitted but came back with an error report. This was because gaussian was unable to gain a correct and therefore optimised transtion state because the the programe has just looked at translation and not roation around the bonds, so it cannot find the correct minima. Instead the proposed un-opitmised structure looks like the chair transition state with crossing connection bonds which is obviously not the minimum transition state.It is therefore proposed that the molecule has to be rotated so that the product and reactant are of a geometry that is similar and that of which would react in the right circumstances.
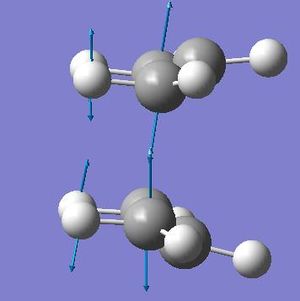
The proposed geometry changes are that central dihedral angle is changed to 0 o and the both central inside angles be reduced to 100 o. This was done to both the product and reactant. The frequency analysis provided the proof we had found a minima with only one negative value which corresponded to the cope reaction itself. This peak was found at -840.13 cm -1 with the intensity of 1.62. This confirmed that the optimisation had worked. The thermochemistry was also obtained form the molecule giving;
Sum of electronic and zero-point Energies= -231.450923 a.u.
Sum of electronic and thermal Energies= -231.445292 a.u.
Sum of electronic and thermal Enthalpies= -231.444347 a.u.
Sum of electronic and thermal Free Energies= -231.479117 a.u.
When comparing them to that of the chair conformation it is seen that the energy is slightly higher for the boat than for the chair, this is to be expected due to the steric strain on the boat conformation.
When looking at both the optimised chair and boat conformations It cannot be directly indicated which of the initial conformers relates to the conformer that undergoes each reaction. Therefore it is proposed that a IRC (Intrinisic Reaction Coordinate) calculation should be carried out. This calculation enables Gaussian to follow the minimal path on the potential energy surface from the transition state to the proposed reactants and therefore give the conformer that would undergo each reaction. This is done by locating a local minima as the potential energy path varies from the transition state. This creates a set of points corresponding to the reaction coordination path which correspond to where the gradient of the energy surface is steepest.
This process was initially done to the optimised chair transition state. The IRC method was selected and it was deemed that only the reverse reaction should be calculated. It was deemed unnecessary to calculate both the forward and backwards direction as the reaction is is symmetrical, and the force constant was calculated once. It was seen that the IRC steps that should be chosen should be 50 steps, this would give the calculation enough steps to compute a reasonable product. On receiving the output it was seen that only 29 steps were computed but in this direction there was no significant 0 platue relating to the products/reactants. The calculation was also tried in the forward direction, this produced the same result but with only 23 calculated. This did not give the plateaux needed to confirm that a reasonable reacntatn/product had been formed. From this stage there were 3 different procedures to try and optimise the product/reactant. The first was to run an optimisation on the end of the IRC, or to run a second IRC from the end result from the previous IRC or finally redo the IRC specifying that you want to compute the force constants at every step. Due to the IRC calcualtion having found a local mimima therefore stoping at 29 steps instead of runnig the full 50 steps the first two options would further more optimise this geometry in the local minima that was found. Therefore only the third option was found to be tried as the other two would not help with further geometry optimisation.
The third option was tried with every step computing a force consatnt, also the calculation was carried out in both directions in order to confirm the symmetry of the reaction that had already been assumed. With this second IRC ther was a significant plateaux around 0 confirming that reactant/products had been formed, and that the IRC calculation had been successful. It was also confirmed that the reaction is perfectly symmetrical with both forwards and reverse reactions producing the same shape and size curves. The differences between the two steps are tablulated below;
| IRC | products/reactants energy/ a.u. | transition state energy/ a.u. | distance between closest termial carbons/ A |
|---|---|---|---|
| intial | -231.692 | -231.619 | 1.55108 |
| force constant calculated at every step | -231.689 | -231.619 | 1.56342 |
It can be seen that the energies of the starting points (transition state) are both the same which is to be expected. The main difference in the two structures obtained from the two different IRC is the slightly lower energy after the force constant is calculated at each step, which corresponds to the slightly shorter distance between the two terminal carbons with it tending towards the the optimum sp 3 bond distance of 1.537 A (3), therefore becoming more stable as a sigma bond is formed.
 |
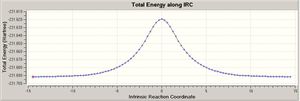 |
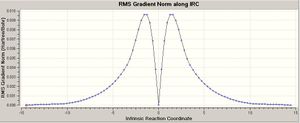 |
This was then seen to give the anti2 is the structure that can be considered the product/reactant of this reaction.
From this the activation energies could be calculated as the initial structure was obtained above. For a correct comparison the transition states were needed to be calculated to B3LYP/6-31G* level of theory. The transition state from the HF/3-21G calculation firstly optimised using TS(Berny) and then the frequency calculated to calculate the thermochemistry properties.
Boat
Sum of electronic and zero-point Energies= -234.351359
Sum of electronic and thermal Energies= -234.345055
Sum of electronic and thermal Enthalpies= -234.344111
Sum of electronic and thermal Free Energies= -234.380125
Chair
Sum of electronic and zero-point Energies= -234.362661
Sum of electronic and thermal Energies= -234.356751
Sum of electronic and thermal Enthalpies= -234.355807
Sum of electronic and thermal Free Energies= -234.391586
All of these energies are approximatly 0.05 a.u higher in energy then would be expected from the comparison with pre calcualted terms. This was also seen to occur when looking at this level of theory on teh reactant/product as well. Therefore it was deemed as they both had this increase their realtive energies were still compatible.
When comparing the geometries of the two different levels of theory they come out with very similar geopmetries. With all observed angles and dihedral angles there was vaiation ofless then 1 o for most of them, and with pre-set bond lengths they remined also nealry unchanged with agreement to many decimal places. The main difference was the differences in the separation of the two fragments with in the low level optimisation only being 2.14 A but this was extnded to 2.25 A for the high level optimisation. This increase shows that although the low level is good at intial optimisations it can be a little out giving higher energy transtion states when lower enegy ones exisit. This increase in fragment distance accounts for the large energy difference in the two levels of theory with the high level being much more stable then the low level theory.
| Conformation | Energy type | HF/3-21G | B3LYP/631G |
|---|---|---|---|
| Chair | Sum of electronic and zero-point energies | -231.466699 | -234.362661 |
| Sum of electronic and thermal energies | -231.461339 | -234.356751 | |
| ΔE at 0K | 0.072842 (45.71) | 0.053591 (33.63) | |
| ΔE at 298.15 K | 0.071228 (44.69) | 0.052201 (32.76) | |
| Boat | Sum of electronic and zero-point energies | -231.450923 | -234.351359 |
| Sum of electronic and thermal energies | -231.445292 | -234.345055 | |
| ΔE at 0K | 0.088618 (55.60) | 0.064893 (40.72) | |
| ΔE at 298.15 K | 0.087275 (54.77) | 0.063897 (40.10) | |
| C i | Sum of electronic and zero-point energies | -231.539541 | -234.416252 |
| Sum of electronic and thermal energies | -231.532567 | -234.408952 |
The numbers in the brackets are related to the energy in kcal/mol for comparison with experimental values. When comparing these to previous computation values obtained and experimental values it can be seen that there is a fairly good agrement with the activation energy being within 2 Kcal/mol from the computational methods and within 2 kcal/mol from the lower boundry of the experimental values. There is a stronger agrement with the chair conformation which has a lower range of experimental values then for the boat conformation. It is also seen that the chair conformation has a lower energy transtion state so it would seen that this reaction would prefer to go through the chair transition state when under kinetic control due to having a lower energy transition state.
Data
Boat B3LYP/631G https://www.ch.ic.ac.uk/wiki/index.php/Image:2_BOAT_TS_OPTFREQ5.LOG
Chair B3LYP/631G https://www.ch.ic.ac.uk/wiki/index.php/Image:2_CHAIR_TS_FROZEN4.LOG
C i B3LYP/631G https://www.ch.ic.ac.uk/wiki/index.php/Image:1ANTI_CI1-FREQ.LOG
Diels Alder Cycloaddition
The following Diels Alder was investigated;

It is considered to be a [4s + 2s] cycloaddition. Within this investigation the transtion state will be obatined and then analysis with particular intrest to its MO's.
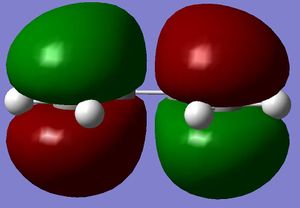
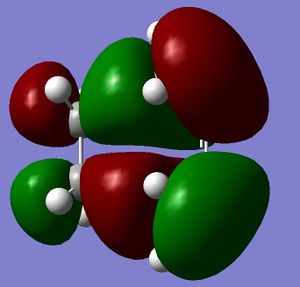
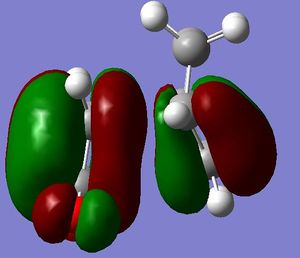
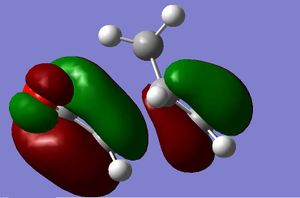
Firstly the largest fragment was optimised (CH2CHCH2) with the HF/3-21G level of theory. By doing this the main fragment was optimised and would make further optimisations quicker and more accurate with less chance of finding a local minima which would not correspond to the actual transition state. The HOMO and LUMO are quoted to the side. The HOMO is seen to have 1 nodal plane and corresponds to a linear combination of the 2 in phase p orbitals with 2 p orbitals in the opposite phase. This is therefore anti-symmetrical (a). The LUMO has 2 nodal planes and is the linear combination of 2 bonding p orbitals on the central carbons and two out of phase p oritals on the terminal carbons, this is given the label symmetrical (s). (all symmetries are quoted in realtion to the plane not the axis) It is also seen that the molecule is completely planar confirming the sp 2 hybridisation, making the molecule completely planar. The energy of the molecule was seen to be 0.0488 a.u. using AM1 semi-empirical molecular orbital method (-154.05 a.u. with 3-21G methods- this level of theory does not hold when looking at the following molecules). The HOMO has the energy -0.3481 a.u., LUMO has energy of 0.01707 a.u. .
After the intial optimisation of the reactant the transition state was optimised. The decided conformation of the transition state was found by using the approxiamtion that it holds similar geometry to the bicyclo system and removing the second cyclic system after intial optimsation(for full picture see https://www.ch.ic.ac.uk/wiki/index.php/Image:Mb_da4.jpg). This was the route used. The method used was AM1 semi-empirical molecular orbital method, using the TS(Berny). I did not choose the frozen method as the transtion state bond lengths from the termial carbons was not known so instead I chose the TS(Berny) starting from near the product bond length and lengthing till reached an optimum transition state. It was seen that the bond length of the newly formed bonds in the product was 1.53Å (2), so for intial attempt for the transition state was taken at 1.8Å, by increasing the bond length it should find the minima of the transtion state. This was too close to the product and just produced the product as the output so a longer bond length was choosen. 2.0 Å was tried and produced a transtion state- like molecule. It was not completely optimised as the negative vibration seen, -93 cm -1 was not seen to correspond to the actaul reaction vibration that was being investigated. 2.2Å was the final attempt, with this attempt there was a negative vibration at -955.97 cm-1 with the intensity of 5.6, and this was seen to correspond to the reaction that was being investigate. It was therefore assumed that the transtion state we had obatined was correct. This transtion state had the energy of 0.1116 a.u. .
 |
 |
 |
 |
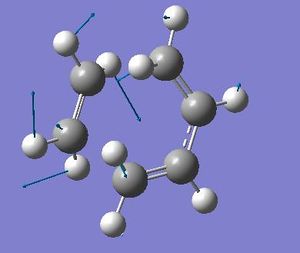
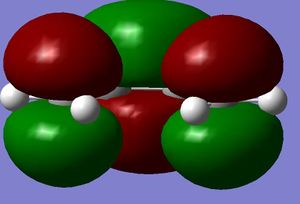
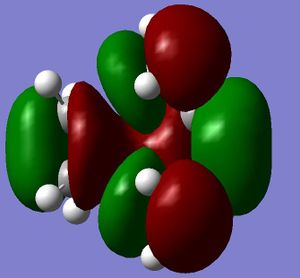
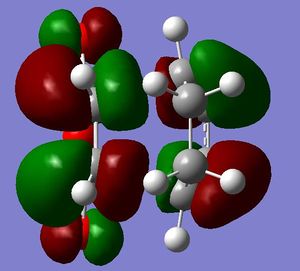
The HOMO and LUMO were then obtained for the transtion state. When looking at the HOMO of the transtion state it can be seen that it is an antisymmetric orbital, and the LUMO is a symmetric orbital.
The geometry of the transition state included the cis- butadiene fragment containining all 3 bonds being nearly the same length ( 1.3818 Å for the old double bonds and 1.3975 Å for the new double bond site), and the bond length of the ethene fragement being extended to 1.3829 Å. The spacing between the terminal ends of the fragments was 2.119 Å. It is known that the optimum sp2 bond length is 1.338 Å. and the sp3 bond length is 1.537 Å (3)with the Van de Waals radii being 1.70 Å (4). Therefore it can be seen that the distance of the new sigma bond at the transition state is not as large as 2 van de Waals radii of carbon, therefore it can be concluded that there is quite a strong interaction between the nuclei but it is still just under 50% more then the sp3 hybridised carbon bond. This interaction would mean that at this point there is a balance point between the replusion of the two nuclei and the attraction from the sigma bond formations. When comparing all the pre-exsiting bonds (of which are all of the same size) it is seen that it is longer then a typical sp2 bond and is therefore an intermidate between the sp2 to sp3.
It was also observed that the bond forming was synchronous and both bonds were formed at the same time concertivly. The next lowest frequency was found at 147.03 cm -1, this corresponded to a twisting motion of the ethene moelcule within the transtion state. This twisting could relate to an asynchronous bond forming, with one bond being made while another is moving away. This one does have a restoring force which drives the vibration back so is seen in the positive region. It is not a true bond forming vibration of the transition due to both bonds not being formed within this vibration.
When thinking of the HOMO of the transition state it can be seen that there is significant bonding in the region of teh new sigma bond formation. This is an indication of the similarities between the product and the reactant. This is clearly showing the mixing of the orbitals to form this new bond which is seen in the reaction.
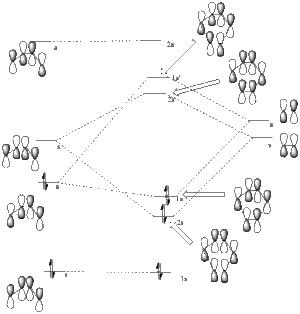
When looking at the MO diagram from the reaction it can be seen that the HOMO and LUMO that are pictured above are the 1a and 2s' respectivly (as per the labelling in the diagram). The intial orbitals that the combined orbtials come from are also stated on the diagram. This shows that the reaction is allowed to occur due to the similar enegies of the mixing orbitals from the two species but also the same symmetries of the orbitals that go on to form the subequent orbitals. It is also allowed as it is the HOMO-LUMO couples that are interacting causing the interaction to be a favourable one.There is also the rule that no two orbitals of the same symmetry can cross during the reaction, whilst orbitals of different symmetry can cross. The favoured pathway is the one which results in a product of the same electronic excitation as the reactant.
Endo vs Exo
The secdon Diels Alder was also investigated with the reaction scheme below. Due to the reaction being proposed to be kinetically controlled the transition state energies are the determining factor as to the output from the reaction.;
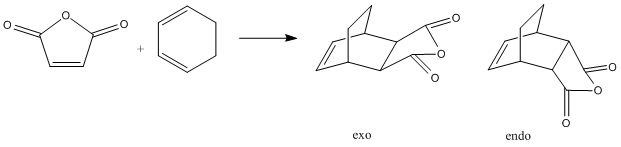
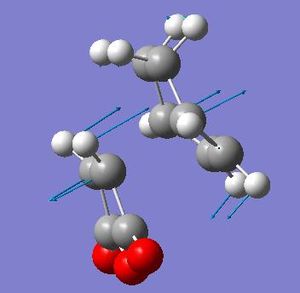
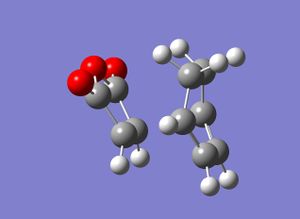
The optimisation was carried out initllay with then AM1 semi-empirical molecular orbital method for these calculations then HF/3-21G level of theory.The method used was the frozen coordinate method, with the bond intially being set to 2.2Å. It was set to this distance as for the last 3 examples 2.2Å has been an approite estimate for a simple C-C sigma bond formation distance so would give approite results.They produced the following geometried with their coresponding transition state vibrations that correspond to the reaction;
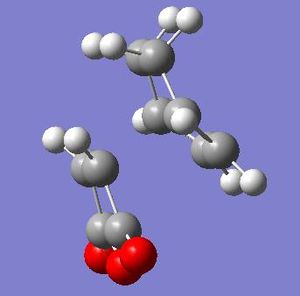 |
 |
 |
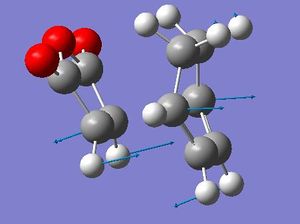 |
endo-
Sum of electronic and zero-point Energies= -605.414904 a.u.
Sum of electronic and thermal Energies= -605.405478 a.u.
Sum of electronic and thermal Enthalpies= -605.404533 a.u.
Sum of electronic and thermal Free Energies= -605.450133 a.u.
exo-
Sum of electronic and zero-point Energies= -605.408140 a.u.
Sum of electronic and thermal Energies= -605.398680 a.u.
Sum of electronic and thermal Enthalpies= -605.397736 a.u.
Sum of electronic and thermal Free Energies= -605.443690 a.u.
From these energies it can be seen that the endo is more stable with exo transition state having a higher energy which is what is expected experimetally. When looking at the bond lengths it is seen that the C-C through space distances between the -(C=O)-O-(C=O)- fragment of the maleic anhydride and the C atoms of the “opposite” is 2.892 Å for the endo product (measuring to the -CH=CH- fragment) but 2.945 Å for the exo product (measuring to the -CH2-CH2- fragment). This reduction in distance between the -(C=O)-O-(C=O)- fragment of the maleic anhydride and the C atoms of the “opposite” for the exo does surgest that the exo is less sterically strained, as this distance is the major factor when considering strain due to the large steric bulk of oxygen and its lone pairs. This indication that it is less strained means that there is another factor stablising the endo product and therefore making it more stable. The H-H distance of the hydrogens on the carbons that make the new sigma bond were also measured. These contribute a little to the strain of the molecule as the are near the sites of the new bond formation, so if they are in the wrong orientation or distance then this will dramtically change the ability of the systme to create a new sugma bond. These distances were seen to be 2.231 Å for the endo product and 2.896 Å for the exo. This also suggests that the exo is more stable with there being less interaction between adjcent hydrogens. There is one way in which the exo could be considered more starined. This would be when considering the hydrogens on the "opposite" fragment to the -(C=O)-O-(C=O)-. Due to the fragment oppisite the -(C=O)-O-(C=O)- fragment in the exo being sp 3 hybridised, the hydrogen is seen to be closer to the -(C=O)-O-(C=O)- fragment, 2.416 Å for the exo where as being only 3.083 Å for the endo at the "opposite" carbon is sp 2. This would give nearly no interactinon for the endo but heavy destablising interaction for the exo.
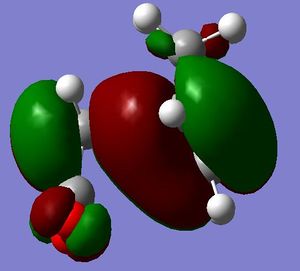
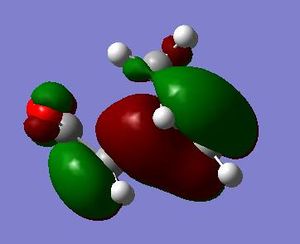
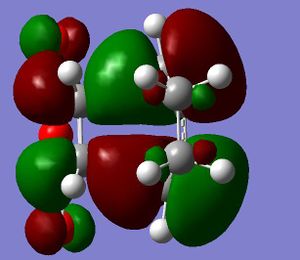
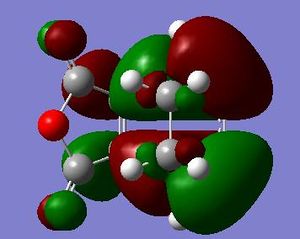
It is seen that the tranastional vibrations are -812.35 cm -1 with an intensity of 96.5 for the exo product and -806.39 cm -1 with an intensity of 71.5 for the endo product. This also confirms that the endo is seen to be more stable as the trnastion state vibration is more positive showing that there is a stronger vibration, and with this vibration not having a restoring force, having a stronger vibration could relate to having a more energetically favoured transtion state. The stability of the endo product is also confirmed when looking at the new sigma bond formed and its length during the transition state. In the endo procust it is 2.162 Å where as it is 2.170 Å in the exo. With the endo having a smaller bond length it could be proposed that in this transtion state it is closer to the products so there is a smaller energy gap. The reasoning behind the smaller distance would be down to the combination of the opposing effects of the steric interaction between the -CH2-CH2- fragment and the maleic anhydride versus secondary orbital interactions between the π systems of -CH=CH- and -(C=O)-O-(C=O)- fragment (which is only really seen in the endo conformation). Here it is seen that the secondary orbital overlap has sufficient amount of stablibsing factor to overcome the sterics involeved with having the endo product. Below are the HOMO and LUMO for the endo and exo to look at the secondary orbital overlap more.
 |
 |
 |
 |
 |
 |
 |
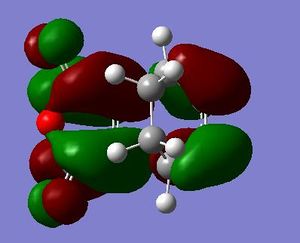 |
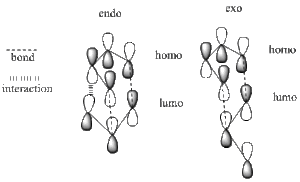
After looking at the MO's there is a vast difference in the way the plane of the (C=O)O(C=O) interacts with the other plane of the cyclic molecule in particular the π systems of -CH=CH-. It can be seen that there is much more interaction with the two planes of the molecule in endo situation then there is in the exo. This is down to secondary orbital overlap.Seconday orbital overlap is defined as the "positive overlap of a nonactive frame in the frontier molecular orbitals of a pericyclic reaction" (5), these orbitals do not create a formal bond but instead contribute to the stability of the molecule. This overlap is not seen with the exo conformation at the -(C=O)-O-(C=O)- fragment is not on the same face as the -CH=CH- fragment so does not produce stability by the linaer combination of the pi systems. This is shown in the diagram on the side. In the MO's it is seen the in the endo the two interaction of the pi systems is face on and there is complete interaction between the whole of the orbitals on the face towards the oposite pi system. With the exo there seems to be "slippage", and the orbitals are no longer completely bonding but some of the front of the orbital now becomes non bonding. It can be seen that by looking at where the pi systems are held that this slippage manes that the pi interaction is lost.
When looking at the HOMO nodes it is seen that both the exo and the endo have a main nodal plan down the plane of symmetry of the molecule (not the MO) this is best seen on the view from above. If you look at the oxygen in the five membered ring then it can be seen that on the endo HOMO there is a small amount of electron density on the oxygen to the same phase as the secondary orbital overlap, being in the same phase this electron desity can be used to stabilise the the overlap more. When looking at the nodal properties of the HOMO between the -(C=O)-O-(C=O)- fragment and the remainder of the system it is seen that in the HOMO in both systems there are no nodes inbetween the two fragments as it is all bonding overlap with the slippage for the exo (as stated above) thereofre giving a smaller electron density for inbetween the two fragments for the exo- only refering to the new sigma bond being formed and no additional stabalisation. In conclusion it can be seen that in this system the secondary orbital overlap plays a large role in stablising the transition state and therefore the products and can be considered the dominating factor. The sterics of the system are a factor that contribute but not to the extent of the stabilising secondary orbital overlap.
Data
intial [4s + 2s] cycloaddition https://www.ch.ic.ac.uk/wiki/index.php/Image:3_OPT_AN1.LOG
endo product https://www.ch.ic.ac.uk/wiki/index.php/Image:4_TS_ENDO_OPT2.LOG
exo product https://www.ch.ic.ac.uk/wiki/index.php/Image:4_TS_EXO_OPT2.LOG
References
(1)Computational Chemistry- Introduction to the Theory and Applications of Molecular and Quantum Mechanics, Errol G. Lewars,: Kluwer Academic Publishers, illistrated edition pp 32
(2)Surface Science, Volumes 566-568, Part 2,20 September 2004,Pages 713-718 doi:10.1016/j.susc.2004.06.004
(3)J M Baranowski, J. Phys. C: Solid State Phys. 19 (1986) 4613-4621.
(4)S. S. Batsanov, Corresponding Author Contact InformationJournal of Molecular Structure: THEOCHEM, Volume 468, Issues 1-2, 9 August 1999, Pages 151-159
(5) Marye Anne Fox,* Raul Cardona, and N. J. Kiwiet, J. Org. Chem. 1987,52, 1469-1474
