Rep:Mod:coke2
Inorganic Computing Lab
Intial Analysis
BH 3
An optimisation was performed on a planar BH 3 molecule with the bond lengths pre set at 1.5 Å. This optimisation was carried out on Gaussian by using the Schrodinger equation to optimise the structure and therefore the energy. This was done using the B3LYP method with the basis set 3-21G. This basis set gives a low degree of complexity and therefore low accuracy but when looking at initial optimisation it is the best set to use to prevent further calculations taking longer than needed. After optimisation the following data was obtained;
Bond length; 1.19 Å
Bond Angle; 120 o
Final Energy; -26.46 a.u.
RMS gradient; 0.000206 a.u.
Dipole Moment; 0 Debyes
Point Group; D3h
Calculation time; 10.0 sec
It is seen that from this data the optimisation has been successful. This can be seen from the RMS (root mean squared) gradient being <0.001 a.u. and the bond length being comparable to the bond length seen in real spectroscopic techniques, 1.202 Å (1). When looking at the optimisation steps that the program undergoes you can see the program zoning in on the minimum energy of the molecule at each step. There are two graphs given in gaussview a) the energy of the molecule as the optimisation proceeds b) gradient of the energy of the molecule at each optimisation. The gradient of this graph corresponds to the tendency of the molecule to be optimised. As the gradient approaches zero it can be seen that each step is minimising the energy less and less indicating that a minima has been found. Each step at this point is only of very slight geometry changes to really gain the optimum.
It should be noted that at the point of optimisation step 1 there are no bonds "drawn in" on gaussview. This is because it exceeds the pre-defined distance as programed into gaussview to be accepted as a bond but does not mean that there is actually no bond. This is a very crude approximation as to what corresponds to a bond- and this only works mainly for organic molecules as this is what gaussview is set up for. It is only an interface to visualise the output from Gaussian so to see if there is a bond the Gaussian file should be read.
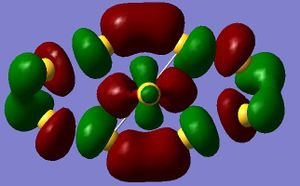
A more comprehensive description of what a bond is defined as should be the point of where orbitals from two separate atoms come within a distance upon where there is sufficient mixing to create new mixed orbitals where one is lower and one is higher in energy then the original set of orbitals. This combining of the orbitals should create an overall lowering of the energy of the filled orbitals creating a more stable species. For this to occur the orbitals need to be similar energy and in the same phase as each other. The strength of the bond is determined by the amount of overlap. This is not only dictated by the distance the orbitals are form each other but also the geometry of each orbital. Therefore it can be concluded that gaussview does not fully take into account that for larger molecules the orbitals that are involved are more diffuse therefore there apparent lengths can be much more then by the pre-set amount on gaussview.
MO descriptions
Below are the description of the orbitals obtained when the orbitals where visualised from the optimisation as per the begining of the page.
 |
 |
 |
 |
 |
 |
 |
 |
(it should be noted that Mo number 5 has been rotated 90 o so the planar molecule is no longer in the plane of the screen but "sticking out" this is so the orbital can be seen more clearly).
The first orbital seen is the 1a 1' orbital ( energy= -17885 KJ/mol) this orbital is the non bonding 1s orbital on the boron. It can be seen that the orbital is held closely to the centre of the molecule and there is high electron density there. From this molecular orbital diagram it can also be seen that there is no interaction between this orbital and the hydrogens, showing that they do not contribute to this orbital making it a non bonding orbital. The reasoning for the hydrogens having no interaction with this orbital is due to the energy level being a lot lower then that of the hydrogen so no mixing can occur. The next orbital is 2a 1' orbital (-1249 KL/mol), it is similar in shape to the previous orbital but now it is clear that the hydrogens are involved strongly with the bonding, with the hydrogens being fully engulfed in the orbital. The next molecular orbitals 3 and 4 are degenerate so have the same energy (861 KJ/mol). The next orbital is the non bonding 1a 2 ' '(-230 KJ/mol) which comprises of the empty p orbital on the boron. The next orbital is the 3a 1 ' orbital it is also unfilled and an anti-bonding orbital. As you can see the orbitals are becoming more diffuse as they are further away from the electron density. The final orbital analysed is the 2e' doubly degenerate anti-bonding orbital. This is an anti-bonding orbital and has an energy of 278 KJ/mol. So by looking at the overall orbital descriptions there is good agreement with the LCAO and their pictorial expression of the orbitals from Gaussian. The only discrepancy is the unfilled orbitals which show slightly different geometry then what would be expected. This could be explained by the unfilled orbitals not having any electron density associated with them so therefore the geometry is not a fixed geometry. The factor that determines the geometry is mainly due to balancing out the orbitals that have associated electron density.
This overall makes the qualitative MO desciption very good at looking at the filled orbitals, but there is variation when looking at the unfilled orbitals when comparing to the qauntitative. The reason behind this is due to the unfilled orbitals being only a mathematical counterbalance for the filled orbitals their actual geometry is undefined until there is electron density to define the area. But the action of filling the orbital changes the geometry of the molecule moving the geometry towards the quantitative desciption as the electron desity would "pull" the orbitals back into the moer defined shape expected.
(note; picture on right needs to be clicked on and then the empty space needs to be clicked on to find the image)
Vibrational Analysis
Vibrational analysis was carried out on the molecule using the same method and basis set as the optimisation. The frequency calculations were calculated on the optimised molecule. The results are below;
| Number | Form of vibration | description | frequency / cm -1 | intensity | Symmetry D 3h point group |
|---|---|---|---|---|---|
| 1 |  |
hydrogens move up and down out of the plane of the molecule whilst moving towards each other on moving upwards, at the same time and concerted, the boron centre stays stationary | 1144.15 | 92.87 | A 2 ' ' |
| 2 |  |
2 bottom hydrogens move down and towards each other in phase with each other, the top hydrogen and boron stay stationary | 1203.64 | 12.31 | E |
| 3 |  |
top hydrogen moves side to side in the plane of the molecule and bottom 2 hydrogens "rock" with both moving clockwise at the same time in the plane of the molecule | 1203.64 | 12.31 | E |
| 4 |  |
all hydrogens moving in the plane of the molecule all together and in concerted motion, moving towards then away from the boron centre | 2598.42 | 0.00 | A 1 ' |
| 5 |  |
bottom two hydrogen move separately and in opposite to each other away then towards the boron centre, all in the plane of the molecule | 2737.44 | 103.74 | E |
| 6 |  |
bottom 2 hydrogens move together towards the boron centre where top hydrogen moves away from boron centre all in the plane of the molecule | 2737.44 | 103.73 | E |
It is clear to see that there are only 3 peaks seen in the IR obtained. This is because frequency of 2 and 3 are the same as are the frequencies of vibrational forms 5 and 6. This gives rise to these peaks having twice the intensity as they are superimposed upon each other. The reason vibration 4 is not seen in the spectra is because there is no change in dipole moment within the molecule. Without this net change it is not "active" to IR as the IR spectrometer will only pick up the vibrations that induce this change in dipole moment, hence vibration 4 has an intensity of 0.
BCl 3
The BCl 3 molecule was computed but with restricted symmetry which was set to D3h with very tight tolerence (0.0001). With this molecule a pseudo-potential was used, this is mainly used for when we are using larger basis sets which are required for computing most inorganic complexes with main group metals in them. An optimisation was then performed using the B3LYP method and the D95V basis set for first row atoms and Los Alamos ECP for heavier atoms. This is a medium basis set.
Bond length; 1.87 Å
Bond Angle; 120 o
Final Energy; -69.44 a.u.
RMS gradient; 0.000059 a.u.
Dipole Moment; 0 Debyes
Point Group; D3h
Calculation time; 8.0 sec
With this data it can be seen that the data has been optimised. It shows okay agreement to the litreture values of the bond length of 1.74 Å (1) and with a bond angle of 120 0. The optimisation was confirmed by the vibrational analysis with all the frequencies being positive and the log file confirming optimisation.
It should be noted that both the optimisation calculation before and this frequency calculation are both done on the same basis and method. This is beacsue this makes the results comparible and for the same geometric molecule. To use a higher degree of accuracy for the vibrational analysis would mean that there would be a difference in the basis set and the results obtained would not be comparible to the moleulce obtained in the optimisation. They would not be comparible as the frequency calculation can be seen as the second derivative of the energy surface so to use a difference basis set would mean that the differential would produce different results. Also by using the output of the optimisation and then doing frequency analysis on that output there is reduced waiting times for analysis as they both comply with each other.
The resoning for frequency analysis is to ensure that the structure obtained and analysed is the minima and not another geometry where the energy surface of the optimisation has a gradient of 0 i.e. point of infelction, maxima. By analysing all the frequncies and checking that they are all positive then this is confirming the optimisation is a minima as the frequency of the vibration is the second defferential of the energy surface (a maxima would produce a set of negative values)
The symmetry that you would expect from this ground state structure would be D3h .The symmetry that gaussview use is D3h. This concludes that the geometry is very exact in gaussview and fits the expected quantitate view on the geometry that would be expected. This also shows that gaussview can be constrained to the intial geometry so the results obtained can be local minima which are of that point group and not the real minima which could be of a different point group. Although this could have happened here from litreture data it is seen that this is the real minima.
The vibrations are seen below. They show similarities to the BH 3 as both molecules have the same geometry. When comparing the vibrations, similar vibrations have the same symmetry labels.
| Number | Form of vibration | frequency cm -1 | intensity |
|---|---|---|---|
| 1 |  |
214 | 3.9 |
| 2 |  |
214 | 3.9 |
| 3 |  |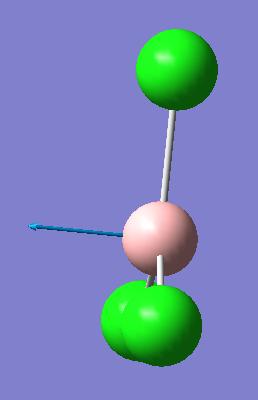
377 | 43.7 |
| 4 |  |
417 | 0.00 |
| 5 |  |
939 | 258 |
| 6 |  |
939 | 258 |
Data
BH 3 optimisation https://www.ch.ic.ac.uk/wiki/index.php/Image:Maddison_Coke_BH3_OPT.LOG
BH 3 frequency analysis https://www.ch.ic.ac.uk/wiki/index.php/Image:Maddison_Coke_BH3_FREQ.LOG
BH 3 molecular orbital analysis https://www.ch.ic.ac.uk/wiki/index.php/Image:Maddison_coke_BH3_POP3.LOG
BCl 3 optimisation https://www.ch.ic.ac.uk/wiki/index.php/Image:Maddison_Coke_BCL3_OPT.LOG
BCl 3 frequency analysis https://www.ch.ic.ac.uk/wiki/index.php/Image:Maddison_Coke_BCL3_FREQ.LOG
Organometalic Complex
In this module the aim is to try and model a complex that was met in 2nd year, Mo(CO) 4(PPh 3) 2 and look at optimising the complex followed by susequent freqency analysis to look at the diffence in vibrational bands seen. This complex is too large to compute at this time with the Ph group adding a large amount of complexity that is not needed to analyse the difference in vibrational bands. Instead the Ph is replaced with Cl and the complex that is being analysed becomes Mo(PCl 3)2(CO) 4.
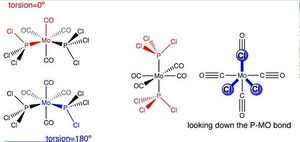
An intial optimisation was carried out but this was deemed to not be the minima of the whole system but a minima that was close to the starting position. This optimisation was carried out using B3LYP method and the low level basis set LANL2MB, with loose convergence set to the system. A second optimisation was carried out using the same method but this time it was not to lose convergence instead it was to increased electronic convegence optimising the chance of getting the best minima of the system. It also used a different basis set, LANL2-DZ, this was needed as it is a higher level basis set and therefore suits the higher convergence criteria that we have imposed in the system. Setting the begining position to a pre-defined starting point under the guidence of Dr Patricia Hunt the following starting positions were used;
After this second optimisation the geometries were compared for the two compunds.
| Geometry | Cis- Mo(PCl 3)2(CO) 4 / Å | Trans- Mo(PCl 3)2(CO) 4/ Å | Literature/Å |
|---|---|---|---|
| P-Mo bond length | 2.51 | 2.45 | 2.53 |
| P-Cl bond length | 2.24 | 2.24 | - |
| Mo-C bond length | 2.08 | 2.06 | 2.04 |
| C=O bond length | 1.175 | 1.172 | 1.13 |
The literature used was as stated in (3), a Mo(CO) 5 L complex. Although this is not ideal as it involves 5 carbonyls instead of 4 it was the best fit I was alble to find in the time given. From the literature it can be seen that there is a fairly good agrement between the literature and the observations from computing giving an intermidate bond length for some of the molecules.
The main varitaion in bond lengths was in the Mo-P bond length, in the cis complex it was much higher then the trans. This will be because the cis isomer experiences much more steric strain due to its bulky groups so has to comprimise between steric clash and bond strength. The other bond lengths seen are nearly the same as the ligands are the same in both complexes.
The bond lengths were not the only thing that differed in the geometry. When looking at the cis isomer it can be seen that when looking down the axis with 2 carbonyls on the distribution of the groups is not even around the centre i.e all the bond angles are not 90 o. Instead the P-Mo-P bond angle was 94 o and the opposite C-Mo_C angle was 87 o. This is due to the steric bulk of the PCl 3 ligand which imposes more strain upon the molecule forcing it off the prefered perfect octahedral with 90 o to all ligand. The trans isomer did not have this effect with the strain being evenly distributed among the four carbonyls from both sides so all bond angles remained 90 o. The other main difference between the geometries is the rotaion of the PCl 3 groups with relation to each other. It can be seen that the trans shows that the groups completely eclipse each other where as in the cis molecule they are anti-parallel to each other. For the cis group this is to reduce steric strain as they can "fit" better together in this conformation.
After the frequency analysis is was easy to see which isomer was more stable by comparison of their relative energies.
Trans- Mo(PCl 3)2(CO) 4= -1637024 KJ/mol
Cis- Mo(PCl 3)2(CO) 4 = -1637027 KJ/mol
This gives as the most stable isomer to be the cis isomer. This would be because in the trans complex the CO back-bonding with the metal centre "pulls out" the electron density of the the complex making the orbitals more diffuse and creating weaker bonds within the molecule. This effect compensates for the largeer dipole moment and sterics that are present due to the molecule being in the cis conformation. The cis complex does feel this effect of the carbonyl withdrawing electron density but it does not have as much effect due to the carbonyl "pulling" the electrons all in the same direction making the orbital not as diffuse as the trans.
The energy difference between the two isomers is only 2 KJ/mol. This is not a significant energy barrier, at room temperature there would be free conversion between the two isomers (RT= 2.5 KJ/mol). To better "fine tune" the reactivity of this metal centre there are things that can be done to the ligands attached. By changing the PR 3 ligand, the reactivity changes which create larger energy gaps between the isomers and creates a more stable isomer. Ways in which this can be done would be to either put larger bulkier groups on the phosphors or to put more electron donating groups onto the phosphors. If larger bulkier groups were put onto the phosphors then the trans would be prefered, the larger the groups attached then the larger in energy the isomers would be. You could control this difference by the size of the group. By adding an electron rich group through the phosphorus the metal centre would have more electron density so would be able to back bond more with the C=O. With this increase in back-bonding the electron desity would be drawn out more so there would be an even more diffuse orbital compared to the cis conformer with the same ligands. This would therefore induce the cis conformation. There is obviously a maximum amount of back-bonding the -C=O can take but until that point the reactivity and conformer preference could be adjusted.
There are some which have very low frequencies in my compounds which are pictured below;
| Form of vibration - cis | frequency/ cm -1 | intensity | Form of vibration - trans | frequency/ cm -1 | intensity | |
|---|---|---|---|---|---|---|
 |
10.77 | 0.026 |  |
5.14 | 0.0941 | |
 |
17.63 | 0.0074 |  |
6.12 | 0.0001 |
At room tempreture you would expect these vibrational modes to be very active and happening a lot as they are low energy so easily excitable. They are very accesible excited states, this is due to them only being roataions of the Cl groups as one unit, this does not require much energy. The lowest energy vibration seen is where both groups move in the same direction all together, this does not create any additional steric clash or interfere with the rest of the molecule so is very low energy.
The main point of comparison between these two compounds is the carbonyl IR peak in the compound. The literature values stated are from my 2nd year lab for Mo(PPH 3)2(CO) 4 so may vary slightly but should give an idea as to the accuracy of the computing carried out.
| frequency for trans/ cm -1 | intensity | literature value | frequency for cis/ cm -1 | intensity | literature value | description of vibration (looking down P-Mo-P bond) |
|---|---|---|---|---|---|---|
| 1950.27 | 1474 | 1891 | 1945.30 | 762 | 1780 | axial set of carbonyls vibrating together |
| 1950.90 | 1466 | - | 1948.64 | 1498 | 1839 | equitorial set of carbonyls vibrating together |
| - | - | - | 1958.35 | 632 | 1888 | the axial carbonyls compressing when the equitorial carbonyls expand |
| - | - | - | 2023.29 | 597 | 2012 | all carbonyls vibrating in phase |
This shows fairly good agrement bewteen the observations on the computer and in the lab with only the first vibration. The reason there is only one vibration seen in the lab for the trans complex is that the resolution of the IR is not of the degree where it can pick up vibrational differences of that order so this peak seen in the lab is seen as the superposition of both of these peaks. The difference in the number of peacks seen is down to the point group of the molecule with the trans being D 4h and the cis being C 2v. This difference in point group makes various vibrations that are seen in the cis not IR "active" in the trans and it has a higher degree of symmetry so more vibrations are considered the "same" so do not produce seperate peaks.
Data
(optimisation given is secondary optimisation)
Trans- Mo(PCl 3)2(CO) 4 optimisation http://hdl.handle.net/10042/to-2678
Cis- Mo(PCl 3)2(CO) 4 optimisation http://hdl.handle.net/10042/to-2677
Trans- Mo(PCl 3)2(CO) 4 frequency analysis http://hdl.handle.net/10042/to-2680
Cis- Mo(PCl 3)2(CO) 4 frequency analysis http://hdl.handle.net/10042/to-2679
Mini Project
I have chosen to look at sulfido complexes. These are one of the more interesting types of complexes due to the sulphurs ability to catenate so there is a large variation in structures it is able to form. The avalibility of the low lying 3d orbitals allows sulphur to act as a good pi acceptor and therefore have a preference for metal centres that are not highly oxidising.
The molecule series I wish to look into are the following;
CrS(S 4)2 2-
MoS(S 4)2 2-
WS(S 4)2 2-
This is to look at the variation of the metal centre size and how this effects the strain on the ring and the strength of the bonds seen. The second related series investigated was the series;
MoS(S 2)2 2-
MoS(S 3)2 2-
MoS(S 4)2 2-
MoS(S 5)2 2-
Here the focus is on the variation on the ring geometry as the ring gets larger and its comparison to already known sulphur rings. I was also to look at the strain on the ring as it gets larger to see if the metal centre still has an effect at larger rings.
Series 1
This series was computed with the method B3LYP method and LANL2-DZ basis set (LANL2MB was first obtained but then optimised again using this higher basis set to gain a better and more accurate geometry and energies for comparison). The first compound that was optimised was the MoS(S 4)2 2- complex which geometry has already been documented (5). This was beacsue it had a know geometry in literature so would be easier and quicker to compute. It was then optimised using the method above. Once optimised the metal centre was changed to the various metal centres to be investigated , by doing it this method computing time was reduced as the difference in the geometry between the metal centres would be minimal. The following results were found; (note the numbering is as follows when looking at the 1st ring on the left number 1 is the bottom right sulphur and then numbered in a clockwise direction, the right ring is inverted through the Mo centre i.e starting at the left top sulphur still clockwise)
Geometry
| Result | Cr | Mo | W |
|---|---|---|---|
| energy/ a.u | -177.40 | -158.70 | - 159.01 |
| RMS/ a.u | 0.000014 | 0.000026 | 0.000016 |
| Dipole moment/ Debeys | 0.41 | 0.53 | 0.81 |
| Time | 3min 9 | 3min 18 | 8min 56 |
| Geometry from above | 22-_from_above.jpg) |
22-_from_above.jpg) |
22-_from_above.jpg) |
| Geometry from the side | 22-_from_side.jpg) |
22-_from_side.jpg) |
22-_from_side.jpg) |
| S 1-M /Å | 2.34 | 2.41 | 2.39 |
| S 1-S 2/Å | 2.36 | 2.44 | 2.47 |
| S 2- S 3/ Å | 2.29 | 2.25 | 2.25 |
| S 3-S 4 /Å | 2.35 | 2.38 | 2.41 |
| S 4-M/ Å | 2.36 | 2.47 | 2.44 |
| S-M (not ring)/Å | 2.04 | 2.18 | 2.18 |
| M- S 1- S 2 / o | 113.3 | 114.9 | 115.5 |
| S 1- S 2 -S 3/ o | 99.1 | 99.6 | 100.1 |
| S 2- S 3 -S 4/ o | 98.2 | 99.8 | 101.3 |
| M- S 4- S 3/ o | 106.8 | 107.7 | 109.55 |
The first thing that sould be seen from the geometry analysis is that they all have a similar shape but the angles and bond lengths are the only varying factor of the geometries. They all adopt a twisted 5 member cyclic shape with the rings from each side of the metal centre twisting in opposite direction. It should be noted that the rings are not symmetric but are slightly skewed to opposite side from one another.
From looking at this summary and the geometry analysis it is seen that the Cr complex is the most stable of the series. When focusing on the energies it is seen that it is much lower than the other two complexes with the W and Mo complexes just having a smaller difference in energy implying that the increase in the centre size is having less effect on the overall complex past a point. It should also be noted that S-W bonds do have slightly better pi interactions then Mo-S bonds (2) this would compensate for the increase in strain from the molecule having an increase in metal centre size and the increase of dipole moment. The stability of the complex can be justified through the geometry of the ligands as well as the dipoles seen. The Cr complex has the smaller dipole as the metal centre has less electron density to distribute. With the susequent complexes in the series the geometry is similar but a significantly larger dipole is seen- this is beacuuse the metal centre has much more electron density to distribute unevenly throughout the complex so would increase the dipole moment. The direction of the dipole moment is the the direction of the Mo-S bond (not in ring)
The geometry aspect can be seen through the comparison of the S-S bond length to that of the sulphur crown, 206pm. Although this is a larger ring it is the most stable configuration of sulphur and is found naturally- so would represent the prefered geometry of the sulphur catenate. When comparing the S-S bonds to this value it is seen that the Cr complex is the closest although still larger representing a weakening in the bond and the strain inforced on the bond due to it being in a smaller cyclic enviroment and the metal centre holding the complex in. This comparison also supports the increase in energy over the series due to the S-S bond length getting further from the optimum distance. The final point of comparison is the metal-S bond that enforces the fact that there is a stronger pi interaction between the W-S than the Mo-S as the bond length is shorter for the W. The Cr is still the shortest bond and therefore enforces the stability of the molecule. This extra stability from the tungston therefore creates a counter balancing force to the destablising effects of the ring strain that is getting larger as the metal centres increase therefore giving comparable energies.
There is a bond length quoted that has an opposite pattern across the series to the other bonds which are getting weaker as the metal centre increases, this is the bond S 3- S 4 . This bond appears to get stronger and shorter as there is more strain on the ring. This could be because as the other bonds are weakening the extra electron density that is no longer held in that bond between the metal centre and the first sulphur, is then pumped onto this empty orbitals on the neighbouring sulphur making it shorted compared to the other bonds. As there is more strain and weaker bonds with the metal centre as the metal centre size increses there is more electron density to be moved into the empty orbitals in the sulphur .
The angles that are seen within the complex series are all very similar for the S-S-S bonds with only a 1 o change over the series. The optimum angles taken from the approximation of having a comparible angle to that of the S 8 crown would be 108 o and it is seen that with the increasing size of the metal centre the angles approch this. This is only a small change in the angle over the series as most of the complexes are optimising the angle replusion by lengthing the bonds- therefore it would suggest that the angles are only contributing a little to the overall energies. There is a larger difference over the series with the Mo-S-S but there is less comparison with the optimum sulphur crown comparison. Although there is no comparison with the sulphur crown, it can be seen that by increasing these angles, the two rings are slowly getting closer together, this has a destablising effect.
Frequency Analysis
The frequency analysis was done on the same method and basis set as the optimisation. The results were as follows;
(only the peaks with intensities above 20 were considered- the vibrations were similar in each case so only one picture is noted )
| Result | Cr | Mo | W |
|---|---|---|---|
 |
- | 285 (20) | 288 (20) |
 |
335 (24) | 323(18) | 304 (12) |
 |
354 (15) | 327 (19) | 320 (18) |
 |
392 (20) | 414(14) | 426 (11) |
 |
547 (90) | 507 (90) | 488 (80) |
(the intensities are marked in brackets)
The observation that the S-S bonds are getting weaker as the metal centre increases in size are confirmed by this analysis. With all apart from the fourth vibration descresing in strength as the series continues. The fourth vibration is the vibration of the S 3- S 4 bond. This bond has already been noted as being a shorted stronger bond then the others in the ring.This IR analysis confirms this and shows that its energy varies a lot over the course of the series.
Mo analysis
The MO analysis was done with the B3LYP method with the basis set LANL2-DZ with addition keyword pop=full to gain full analysis of the molecular orbitals. All orbitals below are viewed from down the S-M bond which is not in the ring.
| Mo | Cr | Mo | W |
|---|---|---|---|
| HOMO -2 |  |
 |
 |
| HOMO-1 |  |
 |
 |
| HOMO |  |
 |
 |
| LUMO |  |
 |
 |
| LUMO+1 |  |
 |
 |
| LUMO +2 |  |
 |
 |
The first thing that should be noted is that all the energies are positive. This means that all the species are highly energetic and fairly unstable. This does not mean the moelcule does not exsit. It is noted that molecules with negative charge can exsit in this form with the HOMO having positive energy. (4)
Next the HOMO and LUMO were analysed. In all 3 cases the HOMO looks very similar which would mean that they all have similar reactivity as a nucleophile. It can be seen that there is a clear d-orbital on the metal centre which is interacting with the orbitlas of the neighouring sulphurs to varying degrees. It should be noted that at this level the energies cannot be directly compared as the heavy metal centre greatly affects the small energy changes so the comparison will mainly be visual and comparison of differences. With the HOMO it can be seen that with the Cr and the W there is a better overlap with the d orbital and neighbouring sulphurs. This positive interaction is bonding and can be seen to lower the overall energy of the molecule. This overlap still occurs in the Mo but is seen to less extent. It is seen that in all of the 3 complexes there is a completly antibonding orbital held by the S 2 in both rings, this highlights the inversion of the rings and the fact that each ring is not symmetric. The LUMO of the series tends to be slightly different along the series, this could be because of the varitation in how closely the orbtials are held to the centre of the molecule, with the smaller Cr producing more defined orbitals where as the Mo and W have slightly more diffuse orbitals which means that they are able to mix in different ways. It shows that in the Cr complex no orbital is seen at this level for S 5 but in the W and Mo complexes these have an orbital that is diffuse and in the plane of the molecule which can then mix with the neighbouring ring. This interaction is bonding but is balanced out by the modes seen from all the sulphurs being out of phase from each other in the plane of the molecule.
Series 2
The next series to be disscused was the expansion of the ring and looking what effect this also had on the geometry of the molecule and the stability of the complex. It is proposed that with a larger ring the strain will be less so the sulphur will be able to adopt the best conformation- approching the crown geometry as the the ring approches 8 members.
The optimisation was carried out using the B3LYP method and to the basis set LANL2-DZ which gave good quility of results and accuracy.The following results were obtained;
Geometry
| Number of Sulphur in ring | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| energy/ a.u | -118.26 | -138.47 | -158.70 | -178.90 |
| RMS/a.u | 0.000026 | 0.000024 | 0.00026 | 0.000023 |
| Dipole moment/ Debeys | 0.89 | 0.16 | 0.53 | 4.61 |
| Time | 1 min 5 | 2min 1 | 3min 18 | 4min 38 |
| Geometry from above | 22-_side.JPG) |
22-_above.JPG) |
|
22-_above.JPG) |
| Geometry from the side | - | 22-_side.JPG) |
|
22-_side.JPG) |
| S 1-M /Å | 2.23 | 2.45 | 2.41 | 2.56/ 2.42 |
| S 1-S 2/Å | 3.73 | 2.38 | 2.44 | 2.29/ 2.39 |
| S 2- S 3/Å | - | 2.38 | 2.25 | 2.31/ 3.77 |
| S 3-S 4/Å | - | - | 2.38 | 2.30/2.20 |
| S 4-S 5/Å | - | - | - | 2.34/2.96 |
| S 5-M /Å | 4.01 | 2.45 | 2.47 | 2.60/ 2.23 |
| S-M (not ring)/Å | 2.27 | 2.19 | 2.18 | 2.17 |
| M- S 1- S 2/ o | 37.3 | 96.2 | 114.9 | 117.4/ 115.1 |
| S 1- S 2 -S 3/ o | - | 84.5 | 99.6 | 106.3/106.9 |
| S 2- S 3 -S 4/ o | - | - | 99.8 | 99.0/ 33.6 |
| S 3- S 4 -S 5/ o | - | - | - | 108.0/ 117.5 |
| M- S 5- S 4 / o | 29.2 | 96.2 | 107.7 | 118.4/ 114.7 |
One of the frst thing to notice is the energy difference. Although gaussview cannot compute relative energies to completely different moleucles it has here been able to compute a series where each addition of a sulphur to both rings has induced a 20 a.u rise in energy, this is consitent through out the series and from the expectation that by adding more atoms to the system, the molecule becomes more complex and rises in energy. It is also a good indication that the molecules obtained are optimised as if they were not optimised then the energy would not have this linear increase.
Out of the 4 molecules studied 2 show slightly different geometries than was expected for comparison although some of them are theortical molecules which would be hard/impossible to sythesise in real life. The complex with the sulphur in a ring of 2 has shown that upon convergence it has now broken away from the expected geometry of having 2 tricyclic rings and 1 sulphur above. It now has a slightly puckered tigonal planar sitting on top of 2 sulphur molecules which have loose interaction with the rest of the molecule. This optimistion was carried out twice from two different starting points, one with the expected disulphur interaction both occuring in the same plane and then another optimisation with the disulphur interaction occuring perpendicular to one another, both of these starting points came back with the same optimisation. When looking at the bond lengths it is seen that they are much larger then the preferred length of 2.1 Å so this also confirms that the geometry seen has very loose interactions between the sulphurs and between the metal centre and the sulphur. This is to be expected as this is a small ring compared to the size of the metal centre so would produce much negative interaction from the steric bulk of the metal centre also the bond angles are very small which would produce a lot of ring strain to which there are no factors that would stablise such a molecule. From this analysis it is seen that there is only a loose interaction between the metal and disulphur.
The other molecule that did not optimise to the expected geometry was the S 5 complex which showed two different ring structures. (above left ring geometries stated before right ring with the numbering as before) The left ring had a similar geometry as what was to be expected with a chair type conformation, but the second ring did not conform to this instead opting for a geometry similar to a 4 membered ring with an extra sulphur displaced above it. This was seen in the first optimisation, thinking that it may have just kept some of the 4 member cyclic conformation from the previous optimisation, the second ring was then set to similar geometry to the left ring, although not identical. This optimisation carried out produced the similar results and these are the ones published. The reasoning of this could be due to a local minima being found or the molecule not being able hold two large rings in the same conformation as the S-Mo-S angle gets larger there would be steric interaction between the two ends of the rings. To reduce this one ring may have to be distorted hence the result.
Therefore the main comparison for the geometries will be of the S 3, S 4 and left ring of S 5. The S 3 complex creates a planar ring with the rings repelled from the top sulphur, this molecule is also very symetric unlike the other rings, S 4 geometry has been stated above and S 5 left ring forms a chair like conformation. When looking at the bond lengths it is seen that overall the metal- sulphur bond is increasing in size as the ring gets larger. This increase in length indicates that the cyclic ligand is slowly becoming less interacted with the metal centre and is more able to be dissociated. This is expected as we approach cyclic ligands that exist as stable cylic allotropes of sulphur. When looking at symmetry S 3 and S 5 are more symmetric then S 4 and this is seen through the bond lengths. The average bond length over the ring ( excluding the S-Mo bond) decreases as the ring gets larger. This would be because the Mo centre is inflicting less strain on the molecule and the sulphur is more flexible to become closer to its optimal bond length. The shortening of the bond length also indicates that the bonds are becoming stronger, this would be because of this release of strain. The bonds that are the stongest are those next to the Mo-S bond. This is because the Mo-S is weaker than a standard bond so the sulphur has a slight excess of electron density which it can use to create a slightly stronger bond with its neighbouring sulphur.
This reduction in strain is also seen in the bond angles, as the ring size is increasing the bond angles are becoming closer to the optimal angle of 108 o. With the rings becoming larger the sulphurs are less constrained and drawn in so are more able to adopt such a geometry.
IR Analysis
Frequency analysis was carried out using the same method and basis set as before (B3LYP, LANL2-DZ) and the following results were obtained; ( frequencies with intensities over 10 were quoted as these are the ones to be seen to compare with experimental data if it was avalible)
| Number of Sulphur in ring | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| 1 | 63 (19) | 220 (21) | 285 (20) | 246 (17) |
| 2 | 313 (11) | 376 (69) | 325 (18) | 308 (10) |
| 3 | 417 (13) | 489 (106) | 327 (19) | 358 (10) |
| 4 | 428 (107) | - | 414 (14) | 378 (25) |
| 5 | 450 (90) | - | 507 (90) | 436 (71) |
| 6 | 468 (134) | - | - | 439 (59) |
| 7 | - | - | - | 516 (70) |
(All of row 1 are not the same type of vibration they are just the first vibration above intensity 10, it has been tablulated for easy of viewing)
Due to the difference in ring size it is difficult to pick out similar vibrations that are seen, this is also due to the symmetry of the molecule. Therefore comparisons between frequencies would not gain much data as the vibrational modes are not comparible so no more data would be obtained.
There is one bond that is comparible with all the complexes through which is the S-Mo bond that is not attached to any ring. This bond is seen to get stronger as the ring size increases. This is seen through both the bond length and the frequency analysis ( the frequency is the last frequency on every frequency set, from S 2 468, 489, 507 and 516 which is S 5). The bond is seen to get stronger as the interaction with the catenated sulphur ring is decreasing. This would be due to the metal having more electron density as the series progresses as less is held in the sulphur ring ligand bond, this extra electron density is used by the metal to form a stronger bond with the sulphur which is preferable due to the sulphur wanting to have double bond like nature to the metal centre as it is only bonded to one centre and prefers to be 2 coordinate.
Further Study
It can be seen that from the above results the data fits the intial theory. To expand this series I could expand the number of sulphur atoms to the ring and then a direct comparison to the sulphur cown could be made with a S 7 ring attached to a metal centre. Another way in which to expand this study would be to combine both series and look at how different metal centers react to increasing the ring size. From this comparison you can compare if ring size increasing changes depending on the metal. By combining both series a better understanding of the series can be obtained.
Data
CrS(S 4)2 2-- optimisation http://hdl.handle.net/10042/to-2735
MoS(S 4)2 2- optimisation http://hdl.handle.net/10042/to-2734
WS(S 4)2 2- - optimisation http://hdl.handle.net/10042/to-2694
CrS(S 4)2 2- - frequency analysis http://hdl.handle.net/10042/to-2741
MoS(S 4)2 2- - frequency analysis http://hdl.handle.net/10042/to-2739
WS(S 4)2 2- - frequency analysis http://hdl.handle.net/10042/to-2695
CrS(S 4)2 2-- MO analysis http://hdl.handle.net/10042/to-2765
MoS(S 4)2 2- MO analysis http://hdl.handle.net/10042/to-2743
WS(S 4)2 2- - MO analysis http://hdl.handle.net/10042/to-2744
MoS(S 2)2 2-- optimisation http://hdl.handle.net/10042/to-2783
MoS(S 3)2 2-- optimisation http://hdl.handle.net/10042/to-2785
MoS(S 5)2 2-- optimisation http://hdl.handle.net/10042/to-2781
MoS(S 2)2 2-- frequency analysis http://hdl.handle.net/10042/to-2784
MoS(S 3)2 2-- frequency analysis http://hdl.handle.net/10042/to-2786
MoS(S 5)2 2-- frequency analysis http://hdl.handle.net/10042/to-2782
Previous project
My intial project was to contain more "real life" molecules so there would be more and better comparison to literature values and more relevance to real life. This included the optimisation of the molecule Mo 2(S 2)62-] and the same molecule with a tungston center. This was to be compared with the MoS(S 4)2 2- as seen above again also with the tungston centre. The formation of the first complex was from the addition of ammonium polysulfide to MoO 4 2-. The point of comparison would be to look at the difference between a S2 and a S 4 ligand and see if enlarging the metal centre had the same effect and to what magnitude this effect was seen. It was proposed that with a more heavily constrained molecule i.e. S 2 there would be more constrain so the larger the metal centre would have more effect on the energies than the S 4 ligand. This part of the project had to be changed due to the Mo 2(S 2)62-] not converging. I was going to replace the Mo with the W after the intial convergence as they would have similar geometries and would reduce the computing time although this never occurred as the molecule never converged. The intial calculations were done to loose convergence (method= B3LYP, basis set= 3-21G, opt=loose). The aim of this was to get a better primary molecule before subjecting it to higher basis sets and therefore reducing overall computing time. This was unsucessful as the molecule returned did not retain any of the double cubic formation as in the beginning and as was expected to be obtained from literature. Although it must be said that there should be little accommodation for variances from literature as this was deemed too far from the actual conformation to be correct. It was therefore decided to return to the intial molecule and manually shift it into a "perfect" cube and perform a higher basis set calculation on it. ( method= B3LYP, basis set= LanL2MB) This returned the result that the computer was unable to compute the result, this was then tried another 3 times with slightly differenet starting points to try and allow the computer to converge the molecule- to which all came back with no result. It was then decided that the molecule may have too much symmetry to be computed by the DFT but instead should be tried with the Hartree Fock analysis. This also came back with no result. At this point it was deemed that the molecule was not able to be computed in the time frame given and resoursecs given. This could be because it is documented that highly symmetrical molecules are not always able to be computed by Gaussian. Below are the loose convergence, the final non converging with DFT and the Hartree Fock approximation;
62-_0ptloose.jpg) |
62-_optfinal.jpg) |
62-_0pthartree_fock.jpg) |
loose converges http://hdl.handle.net/10042/to-2709
final convergence http://hdl.handle.net/10042/to-2711
Hartree Fock aproximation http://hdl.handle.net/10042/to-2710
The other molecule that was to be investigated was the cluster, Fe 4S 4(SR) 4 with R= Me. This was of interest as I looked at the ability of the S to form such clusters and had analogies to cubene which could have also been investigated. The other point of investigation in this molecule was the comparison of the 4 unit cluster to the 2 unit cluster (the 1 unit cluster was not able to be computed due to it giving a multiplicity of doublet and therefore not being able to compute unpaired electrons). The main point was to look at the energies and seen if 2 quintiles of 2 unit cluster was more or less likely than a 4 unit cluster. The 2 unit optimisation was successful and the results are below. The 4 unit cluster was not completely successful. The optimisation was carried out 4 times (3 times with max cycle=50 1 with only internal limit) and it failed to fully converge. The convergence was seen to be getting better each time but after 4 attempts- each lasting up to 4 hours (intial optimisation) it was decided that the convergence was not happening in a quick enough time scale to make continuing with this moleule worth while. The convergence was still occuring though and with more time it may have converged. It was therefore decided that a new project should be started and the results and attempts from previous attempts stated.
 |
 |
 |
2 unit optimisation- http://hdl.handle.net/10042/to-2712
2 unit frequency- http://hdl.handle.net/10042/to-2787
4 unit final convergence- http://hdl.handle.net/10042/to-2788
References
(1) Vicenq Branchadell, Abdelouahid Sbai, and Antonio Oliva J. Phys. Chem. 1995,99, 6472-6476 DOI: 10.1021/j100017a029
(2) Qingwei Zhang, Kerstin Starke, Carola Schulzke, Anja Hofmeister and Jörg Magull Inorganica Chimica Acta Volume 360, Issue 10, 2 July 2007, Pages 3400-3407 doi:10.1016/j.ica.2007.04.027
(3) Kalyani Maitra, Vincent J. Catalano and John H. Nelson Journal of Organometallic Chemistry, 529, 1-2,1997,409-422 doi:10.1016/S0022-328X(96)06599-0
(4) SANDEEP NIGAM, CHIRANJIB MAJUMDER and S K KULSHRESHTHA, J. Chem. Sci., Vol. 118, No. 6, November 2006, pp. 575–578. DOI;10.1007/BF02703955
(5) Shriver and Atkins, Inorganic Chemistry, 4th edition, oxford publishers, pp 451