Rep:Mod:cma209
Week 1
Cope Rearrangement of 1,5-hexadiene -- Reactants/Products Optimisation
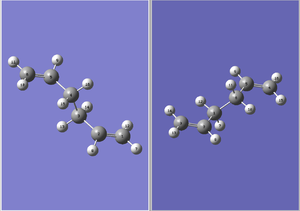
1,5-hexadiene (anti2)
Constructing the molecule
Gaussview was used to draw 1,5-hexadiene. A ethyl fragment was first added to the Molecule screen, and rotated till it resembles a Newman projection.
Subsequently, to ensure an anti linkage, 2 vinyl fragments were used to replace the hydrogens on opposite ends. The dihedral angles are modified such that the C=C bonds are oriented such that they resemble approximately the low energy conformers shown in Appendix 1.
Optimisation
Then, the molecule is cleaned and optimised via the following set-up and submission to HPC portal:
Method: Hartree Fock
Basis Set: 3-21g
| 1,5-hexadiene (Anti2) | |
|---|---|
| File type | .log |
| Calculation Type | FOPT |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Final energy in atomic units (au) | -231.69253523 |
| Gradient | 0.00002918 au |
| Dipole Moment | 0.0000 Debye |
| Point Group | C1 |
| Calculation Time Taken | 1 min 3 sec |
Symmetry: Ci
Item Value Threshold Converged?
Maximum Force 0.000124 0.000450 YES
RMS Force 0.000018 0.000300 YES
Maximum Displacement 0.000892 0.001800 YES
RMS Displacement 0.000306 0.001200 YES
Predicted change in Energy=-7.599488D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.5526 -DE/DX = 0.0001 !
! R2 R(1,3) 1.0848 -DE/DX = 0.0 !
! R3 R(1,4) 1.0856 -DE/DX = 0.0 !
! R4 R(1,7) 1.5089 -DE/DX = 0.0 !
! R5 R(2,5) 1.0856 -DE/DX = 0.0 !
! R6 R(2,6) 1.0848 -DE/DX = 0.0 !
! R7 R(2,12) 1.5089 -DE/DX = 0.0 !
! R8 R(7,8) 1.3161 -DE/DX = 0.0 !
! R9 R(7,9) 1.0769 -DE/DX = 0.0 !
! R10 R(8,10) 1.0734 -DE/DX = 0.0 !
! R11 R(8,11) 1.0747 -DE/DX = 0.0 !
! R12 R(12,13) 1.3161 -DE/DX = 0.0 !
! R13 R(12,14) 1.0769 -DE/DX = 0.0 !
! R14 R(13,15) 1.0734 -DE/DX = 0.0 !
! R15 R(13,16) 1.0747 -DE/DX = 0.0 !
! A1 A(2,1,3) 109.4077 -DE/DX = 0.0 !
! A2 A(2,1,4) 108.3463 -DE/DX = 0.0 !
! A3 A(2,1,7) 111.3501 -DE/DX = 0.0 !
! A4 A(3,1,4) 107.7097 -DE/DX = 0.0 !
! A5 A(3,1,7) 109.9642 -DE/DX = 0.0 !
! A6 A(4,1,7) 109.9762 -DE/DX = 0.0 !
! A7 A(1,2,5) 108.3463 -DE/DX = 0.0 !
! A8 A(1,2,6) 109.4077 -DE/DX = 0.0 !
! A9 A(1,2,12) 111.3501 -DE/DX = 0.0 !
! A10 A(5,2,6) 107.7097 -DE/DX = 0.0 !
! A11 A(5,2,12) 109.9762 -DE/DX = 0.0 !
! A12 A(6,2,12) 109.9642 -DE/DX = 0.0 !
! A13 A(1,7,8) 124.8132 -DE/DX = 0.0 !
! A14 A(1,7,9) 115.5057 -DE/DX = 0.0 !
! A15 A(8,7,9) 119.6732 -DE/DX = 0.0 !
! A16 A(7,8,10) 121.8655 -DE/DX = 0.0 !
! A17 A(7,8,11) 121.8234 -DE/DX = 0.0 !
! A18 A(10,8,11) 116.311 -DE/DX = 0.0 !
! A19 A(2,12,13) 124.8132 -DE/DX = 0.0 !
! A20 A(2,12,14) 115.5057 -DE/DX = 0.0 !
! A21 A(13,12,14) 119.6732 -DE/DX = 0.0 !
! A22 A(12,13,15) 121.8655 -DE/DX = 0.0 !
! A23 A(12,13,16) 121.8234 -DE/DX = 0.0 !
! A24 A(15,13,16) 116.311 -DE/DX = 0.0 !
! D1 D(3,1,2,5) 62.8308 -DE/DX = 0.0 !
! D2 D(3,1,2,6) 180.0 -DE/DX = 0.0 !
! D3 D(3,1,2,12) -58.2382 -DE/DX = 0.0 !
! D4 D(4,1,2,5) 180.0 -DE/DX = 0.0 !
! D5 D(4,1,2,6) -62.8308 -DE/DX = 0.0 !
! D6 D(4,1,2,12) 58.9311 -DE/DX = 0.0 !
! D7 D(7,1,2,5) -58.9311 -DE/DX = 0.0 !
! D8 D(7,1,2,6) 58.2382 -DE/DX = 0.0 !
! D9 D(7,1,2,12) -180.0 -DE/DX = 0.0 !
! D10 D(2,1,7,8) 114.6529 -DE/DX = 0.0 !
! D11 D(2,1,7,9) -64.3192 -DE/DX = 0.0 !
! D12 D(3,1,7,8) -6.7853 -DE/DX = 0.0 !
! D13 D(3,1,7,9) 174.2427 -DE/DX = 0.0 !
! D14 D(4,1,7,8) -125.2363 -DE/DX = 0.0 !
! D15 D(4,1,7,9) 55.7917 -DE/DX = 0.0 !
! D16 D(1,2,12,13) -114.6529 -DE/DX = 0.0 !
! D17 D(1,2,12,14) 64.3192 -DE/DX = 0.0 !
! D18 D(5,2,12,13) 125.2363 -DE/DX = 0.0 !
! D19 D(5,2,12,14) -55.7917 -DE/DX = 0.0 !
! D20 D(6,2,12,13) 6.7853 -DE/DX = 0.0 !
! D21 D(6,2,12,14) -174.2427 -DE/DX = 0.0 !
! D22 D(1,7,8,10) -179.113 -DE/DX = 0.0 !
! D23 D(1,7,8,11) 1.0564 -DE/DX = 0.0 !
! D24 D(9,7,8,10) -0.1808 -DE/DX = 0.0 !
! D25 D(9,7,8,11) -180.0114 -DE/DX = 0.0 !
! D26 D(2,12,13,15) 179.113 -DE/DX = 0.0 !
! D27 D(2,12,13,16) -1.0564 -DE/DX = 0.0 !
! D28 D(14,12,13,15) 0.1808 -DE/DX = 0.0 !
! D29 D(14,12,13,16) 180.0114 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
The optimisation was successful as convergence to a minimum was achieved.
The anti2 conformer has dihedral angles of approximately 120o on both C1-C2-C3-C4 and C3-C4-C5-C6, where C3 and C4 are the middle ethyl fragment while C1, C2 and C5, C6 are the terminal C=C groups. Comparision of energy (-231.69253523 au) with anti2 conformer in Appendix 1 indicates that the correct conformer has been obtained.
Link:DOI:10042/22959
1,5-hexadiene (Gauche structures)
Other 1,5-hexadiene structures were similarly constructed from an ethyl fragment and 2 vinyl fragments. However, as with Newman projection below, the vinyl groups are no longer anti-periplanar but are gauche to one another. Different gauche conformers can be obtained from rotation of vinyl groups on both ends and low energy conformers from Appendix 1 were used as reference. the gauche4 and gauche3 structures were constructed and optimised.
Optimising 1-5-hexadiene (gauche4)
The molecule is cleaned and optimised via the following set-up and submission to HPC portal:
Optimisation Method: Hartree Fock
Basis Set: 3-21g
| 1,5-hexadiene (gauche4) | |
|---|---|
| File type | .log |
| Calculation Type | FOPT |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Final energy in atomic units (au) | -231.69153032 |
| Gradient | 0.00001866 au |
| Dipole Moment | 0.1281 Debye |
| Point Group | C2 |
| Calculation Time Taken | 1 min 47 sec |
Item Value Threshold Converged?
Maximum Force 0.000018 0.000450 YES
RMS Force 0.000008 0.000300 YES
Maximum Displacement 0.001569 0.001800 YES
RMS Displacement 0.000413 0.001200 YES
Predicted change in Energy=-4.919439D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.5553 -DE/DX = 0.0 !
! R2 R(1,3) 1.0852 -DE/DX = 0.0 !
! R3 R(1,4) 1.0846 -DE/DX = 0.0 !
! R4 R(1,12) 1.5099 -DE/DX = 0.0 !
! R5 R(2,5) 1.0852 -DE/DX = 0.0 !
! R6 R(2,6) 1.0846 -DE/DX = 0.0 !
! R7 R(2,7) 1.5099 -DE/DX = 0.0 !
! R8 R(7,8) 1.3164 -DE/DX = 0.0 !
! R9 R(7,9) 1.0757 -DE/DX = 0.0 !
! R10 R(8,10) 1.0734 -DE/DX = 0.0 !
! R11 R(8,11) 1.0748 -DE/DX = 0.0 !
! R12 R(12,13) 1.3164 -DE/DX = 0.0 !
! R13 R(12,14) 1.0757 -DE/DX = 0.0 !
! R14 R(13,15) 1.0734 -DE/DX = 0.0 !
! R15 R(13,16) 1.0748 -DE/DX = 0.0 !
! A1 A(2,1,3) 108.2989 -DE/DX = 0.0 !
! A2 A(2,1,4) 108.7737 -DE/DX = 0.0 !
! A3 A(2,1,12) 112.3874 -DE/DX = 0.0 !
! A4 A(3,1,4) 107.9502 -DE/DX = 0.0 !
! A5 A(3,1,12) 109.8658 -DE/DX = 0.0 !
! A6 A(4,1,12) 109.4551 -DE/DX = 0.0 !
! A7 A(1,2,5) 108.2989 -DE/DX = 0.0 !
! A8 A(1,2,6) 108.7737 -DE/DX = 0.0 !
! A9 A(1,2,7) 112.3874 -DE/DX = 0.0 !
! A10 A(5,2,6) 107.9502 -DE/DX = 0.0 !
! A11 A(5,2,7) 109.8658 -DE/DX = 0.0 !
! A12 A(6,2,7) 109.4551 -DE/DX = 0.0 !
! A13 A(2,7,8) 124.4248 -DE/DX = 0.0 !
! A14 A(2,7,9) 116.0435 -DE/DX = 0.0 !
! A15 A(8,7,9) 119.5293 -DE/DX = 0.0 !
! A16 A(7,8,10) 121.8674 -DE/DX = 0.0 !
! A17 A(7,8,11) 121.8481 -DE/DX = 0.0 !
! A18 A(10,8,11) 116.2841 -DE/DX = 0.0 !
! A19 A(1,12,13) 124.4248 -DE/DX = 0.0 !
! A20 A(1,12,14) 116.0435 -DE/DX = 0.0 !
! A21 A(13,12,14) 119.5293 -DE/DX = 0.0 !
! A22 A(12,13,15) 121.8674 -DE/DX = 0.0 !
! A23 A(12,13,16) 121.8481 -DE/DX = 0.0 !
! A24 A(15,13,16) 116.2841 -DE/DX = 0.0 !
! D1 D(3,1,2,5) 179.4349 -DE/DX = 0.0 !
! D2 D(3,1,2,6) -63.4838 -DE/DX = 0.0 !
! D3 D(3,1,2,7) 57.8803 -DE/DX = 0.0 !
! D4 D(4,1,2,5) -63.4838 -DE/DX = 0.0 !
! D5 D(4,1,2,6) 53.5975 -DE/DX = 0.0 !
! D6 D(4,1,2,7) 174.9616 -DE/DX = 0.0 !
! D7 D(12,1,2,5) 57.8803 -DE/DX = 0.0 !
! D8 D(12,1,2,6) 174.9616 -DE/DX = 0.0 !
! D9 D(12,1,2,7) -63.6743 -DE/DX = 0.0 !
! D10 D(2,1,12,13) -109.4464 -DE/DX = 0.0 !
! D11 D(2,1,12,14) 69.9908 -DE/DX = 0.0 !
! D12 D(3,1,12,13) 129.8974 -DE/DX = 0.0 !
! D13 D(3,1,12,14) -50.6654 -DE/DX = 0.0 !
! D14 D(4,1,12,13) 11.5273 -DE/DX = 0.0 !
! D15 D(4,1,12,14) -169.0355 -DE/DX = 0.0 !
! D16 D(1,2,7,8) -109.4464 -DE/DX = 0.0 !
! D17 D(1,2,7,9) 69.9908 -DE/DX = 0.0 !
! D18 D(5,2,7,8) 129.8974 -DE/DX = 0.0 !
! D19 D(5,2,7,9) -50.6654 -DE/DX = 0.0 !
! D20 D(6,2,7,8) 11.5273 -DE/DX = 0.0 !
! D21 D(6,2,7,9) -169.0355 -DE/DX = 0.0 !
! D22 D(2,7,8,10) 179.2055 -DE/DX = 0.0 !
! D23 D(2,7,8,11) -1.036 -DE/DX = 0.0 !
! D24 D(9,7,8,10) -0.2134 -DE/DX = 0.0 !
! D25 D(9,7,8,11) 179.5451 -DE/DX = 0.0 !
! D26 D(1,12,13,15) 179.2055 -DE/DX = 0.0 !
! D27 D(1,12,13,16) -1.036 -DE/DX = 0.0 !
! D28 D(14,12,13,15) -0.2134 -DE/DX = 0.0 !
! D29 D(14,12,13,16) 179.5451 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
The optimisation was successful as convergence to a minimum was achieved.
Link:DOI:10042/22960
Symmetry Point Group: C2
The gauche4 conformer has dihedral angles of approximately ±109.5o on both C1-C2-C3-C4 and C3-C4-C5-C6, where C3 and C4 are the middle ethyl fragment while C1, C2 and C5, C6 are the terminal C=C groups. Comparision of energy (-231.69153032 au) with gauche4 conformer in Appendix 1 indicates that the correct conformer has been obtained.
Optimising 1,5-hexadiene (gauche3)
The molecule is cleaned and optimised via the following set-up and submission to HPC portal:
Optimisation Method: Hartree Fock
Basis Set: 3-21g
| 1,5-hexadiene (gauche3) | |
|---|---|
| File type | .log |
| Calculation Type | FOPT |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Final energy in atomic units (au) | -231.69266120 |
| Gradient | 0.00001556 au |
| Dipole Moment | 0.3409 Debye |
| Point Group | C1 |
| Calculation Time Taken | 1 min 28 sec |
Item Value Threshold Converged?
Maximum Force 0.000044 0.000450 YES
RMS Force 0.000009 0.000300 YES
Maximum Displacement 0.001380 0.001800 YES
RMS Displacement 0.000491 0.001200 YES
Predicted change in Energy=-3.609980D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.5531 -DE/DX = 0.0 !
! R2 R(1,3) 1.0872 -DE/DX = 0.0 !
! R3 R(1,4) 1.0844 -DE/DX = 0.0 !
! R4 R(1,12) 1.5085 -DE/DX = 0.0 !
! R5 R(2,5) 1.0836 -DE/DX = 0.0 !
! R6 R(2,6) 1.0867 -DE/DX = 0.0 !
! R7 R(2,7) 1.5093 -DE/DX = 0.0 !
! R8 R(7,8) 1.3165 -DE/DX = 0.0 !
! R9 R(7,9) 1.0772 -DE/DX = 0.0 !
! R10 R(8,10) 1.0735 -DE/DX = 0.0 !
! R11 R(8,11) 1.0745 -DE/DX = 0.0 !
! R12 R(12,13) 1.3163 -DE/DX = 0.0 !
! R13 R(12,14) 1.0751 -DE/DX = 0.0 !
! R14 R(13,15) 1.0735 -DE/DX = 0.0 !
! R15 R(13,16) 1.0748 -DE/DX = 0.0 !
! A1 A(2,1,3) 108.6453 -DE/DX = 0.0 !
! A2 A(2,1,4) 109.3261 -DE/DX = 0.0 !
! A3 A(2,1,12) 111.775 -DE/DX = 0.0 !
! A4 A(3,1,4) 107.5309 -DE/DX = 0.0 !
! A5 A(3,1,12) 109.7234 -DE/DX = 0.0 !
! A6 A(4,1,12) 109.738 -DE/DX = 0.0 !
! A7 A(1,2,5) 109.1939 -DE/DX = 0.0 !
! A8 A(1,2,6) 108.4634 -DE/DX = 0.0 !
! A9 A(1,2,7) 111.8673 -DE/DX = 0.0 !
! A10 A(5,2,6) 107.8754 -DE/DX = 0.0 !
! A11 A(5,2,7) 110.2758 -DE/DX = 0.0 !
! A12 A(6,2,7) 109.064 -DE/DX = 0.0 !
! A13 A(2,7,8) 125.0243 -DE/DX = 0.0 !
! A14 A(2,7,9) 115.3003 -DE/DX = 0.0 !
! A15 A(8,7,9) 119.6747 -DE/DX = 0.0 !
! A16 A(7,8,10) 121.8438 -DE/DX = 0.0 !
! A17 A(7,8,11) 121.7797 -DE/DX = 0.0 !
! A18 A(10,8,11) 116.3762 -DE/DX = 0.0 !
! A19 A(1,12,13) 124.5298 -DE/DX = 0.0 !
! A20 A(1,12,14) 115.5492 -DE/DX = 0.0 !
! A21 A(13,12,14) 119.9143 -DE/DX = 0.0 !
! A22 A(12,13,15) 121.7758 -DE/DX = 0.0 !
! A23 A(12,13,16) 121.9606 -DE/DX = 0.0 !
! A24 A(15,13,16) 116.2635 -DE/DX = 0.0 !
! D1 D(3,1,2,5) -175.9065 -DE/DX = 0.0 !
! D2 D(3,1,2,6) 66.7784 -DE/DX = 0.0 !
! D3 D(3,1,2,7) -53.556 -DE/DX = 0.0 !
! D4 D(4,1,2,5) 67.0142 -DE/DX = 0.0 !
! D5 D(4,1,2,6) -50.3009 -DE/DX = 0.0 !
! D6 D(4,1,2,7) -170.6353 -DE/DX = 0.0 !
! D7 D(12,1,2,5) -54.6864 -DE/DX = 0.0 !
! D8 D(12,1,2,6) -172.0015 -DE/DX = 0.0 !
! D9 D(12,1,2,7) 67.6641 -DE/DX = 0.0 !
! D10 D(2,1,12,13) 120.8781 -DE/DX = 0.0 !
! D11 D(2,1,12,14) -58.1813 -DE/DX = 0.0 !
! D12 D(3,1,12,13) -118.5285 -DE/DX = 0.0 !
! D13 D(3,1,12,14) 62.4122 -DE/DX = 0.0 !
! D14 D(4,1,12,13) -0.5848 -DE/DX = 0.0 !
! D15 D(4,1,12,14) -179.6442 -DE/DX = 0.0 !
! D16 D(1,2,7,8) -117.2338 -DE/DX = 0.0 !
! D17 D(1,2,7,9) 62.4576 -DE/DX = 0.0 !
! D18 D(5,2,7,8) 4.4965 -DE/DX = 0.0 !
! D19 D(5,2,7,9) -175.812 -DE/DX = 0.0 !
! D20 D(6,2,7,8) 122.783 -DE/DX = 0.0 !
! D21 D(6,2,7,9) -57.5256 -DE/DX = 0.0 !
! D22 D(2,7,8,10) 179.8706 -DE/DX = 0.0 !
! D23 D(2,7,8,11) -0.3243 -DE/DX = 0.0 !
! D24 D(9,7,8,10) 0.1917 -DE/DX = 0.0 !
! D25 D(9,7,8,11) -180.0032 -DE/DX = 0.0 !
! D26 D(1,12,13,15) -179.4375 -DE/DX = 0.0 !
! D27 D(1,12,13,16) 0.6328 -DE/DX = 0.0 !
! D28 D(14,12,13,15) -0.4166 -DE/DX = 0.0 !
! D29 D(14,12,13,16) 179.6537 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
The optimisation was successful as convergence to a minimum was achieved.
Link:DOI:10042/22953
Symmetry Point Group: C1 The gauche4 conformer has dihedral angles of approximately ±120o on both C1-C2-C3-C4 and C3-C4-C5-C6, where C3 and C4 are the middle ethyl fragment while C1, C2 and C5, C6 are the terminal C=C groups. Comparision of energy (-231.69266120 au) with gauche3 conformer in Appendix 1 indicates that the correct conformer has been obtained.
Optimising 1,5-hexadiene (anti2) at higher basis set
A lower and more accurate minimum could be obtained by subjecting the molecule to a higher basis set. This process however takes longer to complete. The log file of optimised (basis set: 3-21g) 1,5-hexadiene (anti2) was copied into a new molecule window and was further optimised with a better basis set (6-31Gd).
Method: DFT/B3LYP Basis Set: 6-31Gd
| 1,5-hexadiene (Anti2) | |
|---|---|
| File type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d) |
| Final energy in atomic units (au) | -234.61170274 |
| Gradient | 0.00001331 au |
| Dipole Moment | 0.0000 Debye |
| Point Group | C1 |
| Calculation Time Taken | 3 min 29 sec |
Item Value Threshold Converged?
Maximum Force 0.000015 0.000450 YES
RMS Force 0.000006 0.000300 YES
Maximum Displacement 0.000223 0.001800 YES
RMS Displacement 0.000080 0.001200 YES
Predicted change in Energy=-1.591799D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.5481 -DE/DX = 0.0 !
! R2 R(1,3) 1.098 -DE/DX = 0.0 !
! R3 R(1,4) 1.0997 -DE/DX = 0.0 !
! R4 R(1,7) 1.5042 -DE/DX = 0.0 !
! R5 R(2,5) 1.0997 -DE/DX = 0.0 !
! R6 R(2,6) 1.098 -DE/DX = 0.0 !
! R7 R(2,12) 1.5042 -DE/DX = 0.0 !
! R8 R(7,8) 1.3335 -DE/DX = 0.0 !
! R9 R(7,9) 1.0919 -DE/DX = 0.0 !
! R10 R(8,10) 1.0868 -DE/DX = 0.0 !
! R11 R(8,11) 1.0885 -DE/DX = 0.0 !
! R12 R(12,13) 1.3335 -DE/DX = 0.0 !
! R13 R(12,14) 1.0919 -DE/DX = 0.0 !
! R14 R(13,15) 1.0868 -DE/DX = 0.0 !
! R15 R(13,16) 1.0885 -DE/DX = 0.0 !
! A1 A(2,1,3) 109.6058 -DE/DX = 0.0 !
! A2 A(2,1,4) 108.1899 -DE/DX = 0.0 !
! A3 A(2,1,7) 112.672 -DE/DX = 0.0 !
! A4 A(3,1,4) 106.6601 -DE/DX = 0.0 !
! A5 A(3,1,7) 109.742 -DE/DX = 0.0 !
! A6 A(4,1,7) 109.7814 -DE/DX = 0.0 !
! A7 A(1,2,5) 108.1899 -DE/DX = 0.0 !
! A8 A(1,2,6) 109.6058 -DE/DX = 0.0 !
! A9 A(1,2,12) 112.672 -DE/DX = 0.0 !
! A10 A(5,2,6) 106.6601 -DE/DX = 0.0 !
! A11 A(5,2,12) 109.7814 -DE/DX = 0.0 !
! A12 A(6,2,12) 109.742 -DE/DX = 0.0 !
! A13 A(1,7,8) 125.2867 -DE/DX = 0.0 !
! A14 A(1,7,9) 115.7271 -DE/DX = 0.0 !
! A15 A(8,7,9) 118.9815 -DE/DX = 0.0 !
! A16 A(7,8,10) 121.8701 -DE/DX = 0.0 !
! A17 A(7,8,11) 121.6516 -DE/DX = 0.0 !
! A18 A(10,8,11) 116.4778 -DE/DX = 0.0 !
! A19 A(2,12,13) 125.2867 -DE/DX = 0.0 !
! A20 A(2,12,14) 115.7271 -DE/DX = 0.0 !
! A21 A(13,12,14) 118.9815 -DE/DX = 0.0 !
! A22 A(12,13,15) 121.8701 -DE/DX = 0.0 !
! A23 A(12,13,16) 121.6516 -DE/DX = 0.0 !
! A24 A(15,13,16) 116.4778 -DE/DX = 0.0 !
! D1 D(3,1,2,5) 64.0627 -DE/DX = 0.0 !
! D2 D(3,1,2,6) 180.0 -DE/DX = 0.0 !
! D3 D(3,1,2,12) -57.4932 -DE/DX = 0.0 !
! D4 D(4,1,2,5) 180.0 -DE/DX = 0.0 !
! D5 D(4,1,2,6) -64.0627 -DE/DX = 0.0 !
! D6 D(4,1,2,12) 58.4441 -DE/DX = 0.0 !
! D7 D(7,1,2,5) -58.4441 -DE/DX = 0.0 !
! D8 D(7,1,2,6) 57.4932 -DE/DX = 0.0 !
! D9 D(7,1,2,12) 180.0 -DE/DX = 0.0 !
! D10 D(2,1,7,8) 118.5279 -DE/DX = 0.0 !
! D11 D(2,1,7,9) -60.6757 -DE/DX = 0.0 !
! D12 D(3,1,7,8) -3.9023 -DE/DX = 0.0 !
! D13 D(3,1,7,9) 176.8941 -DE/DX = 0.0 !
! D14 D(4,1,7,8) -120.8239 -DE/DX = 0.0 !
! D15 D(4,1,7,9) 59.9725 -DE/DX = 0.0 !
! D16 D(1,2,12,13) -118.5279 -DE/DX = 0.0 !
! D17 D(1,2,12,14) 60.6757 -DE/DX = 0.0 !
! D18 D(5,2,12,13) 120.8239 -DE/DX = 0.0 !
! D19 D(5,2,12,14) -59.9725 -DE/DX = 0.0 !
! D20 D(6,2,12,13) 3.9023 -DE/DX = 0.0 !
! D21 D(6,2,12,14) -176.8941 -DE/DX = 0.0 !
! D22 D(1,7,8,10) -179.5641 -DE/DX = 0.0 !
! D23 D(1,7,8,11) 0.7139 -DE/DX = 0.0 !
! D24 D(9,7,8,10) -0.3842 -DE/DX = 0.0 !
! D25 D(9,7,8,11) 179.8938 -DE/DX = 0.0 !
! D26 D(2,12,13,15) 179.5641 -DE/DX = 0.0 !
! D27 D(2,12,13,16) -0.7139 -DE/DX = 0.0 !
! D28 D(14,12,13,15) 0.3842 -DE/DX = 0.0 !
! D29 D(14,12,13,16) -179.8938 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
The optimisation was successful as convergence to a minimum was achieved. The minimum energy obtained using this basis set is lower (-234.61170274 au) compared to the minimum energy obtained using the lower basis set (-231.69253523 au). This indicates that the higher basis set has indeed provided us with a lower and more accurate minimum energy.
Link:DOI:10042/22962
The optimised conformer has dihedral angles (±118o) that is closer to 120o on both C1-C2-C3-C4 and C3-C4-C5-C6, as compared to that of the lower basis set optimisation (±115o). As before, C3 and C4 are the middle ethyl fragment while C1, C2 and C5, C6 refer to the terminal C=C groups. This also indicates that a better optimisation has been obtained using the higher basis set, as dihedral angles obtained are closer to the ideal theoretical dihedral angle of 120o that gives the minimum energy.
Frequency calculation of 1,5-hexadiene (anti2)
A frequency calculation is crucial in the determination of whether or not a minimum has been reached. The frequency analysis is essential the second derivative of the PES of a reaction, and if all frequencies obtained are positive, a minimum is reached. A transition state is reached if one of the frequencies obtained is negative. Optimisation is incomplete or failed if more than one negative frequencies have been obtained. Also, frequency analysis provides information with IR-active or Raman-active vibrations could be detected and compared with experimental values.
Using 6-31G(d) optimised 1,4-hexadiene (anti2), a frequency calculation is set-up:
Method: DFT/B3LYP
Basis Set:6-31Gd
| 1,5-hexadiene (Anti2) | |
|---|---|
| File type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d) |
| Final energy in atomic units (au) | -234.61170274 |
| Gradient | 0.00001338 au |
| Dipole Moment | 0.0000 Debye |
| Point Group | C1 |
| Calculation Time Taken | 3 min 27 sec |
Symmetry: Ci
Link:DOI:10042/22964
Low frequencies Table
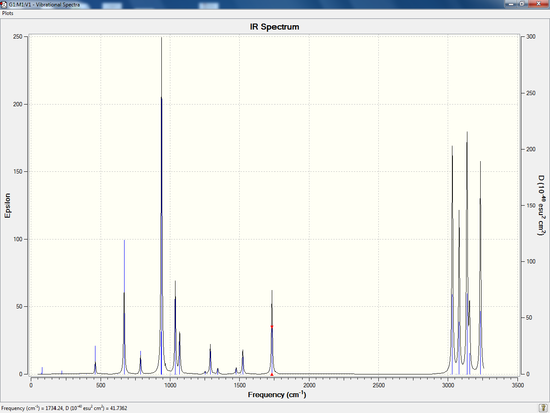
Low frequencies --- -18.8017 -11.7161 -0.0012 -0.0010 -0.0006 1.7416 Low frequencies --- 72.7187 80.1386 120.0141
The first vibration listed is 72.7187cm-1 which is real. There are no imaginary frequencies obtained. All frequencies obtained are real nad positive, therefore, a minimum has been reached.
IR Spectrum
The vibrations could be visualised via an IR Spectrum, though only IR-active vibrations can be observed. For a vibrational mode to be considered IR-active, it must undergo a change in a dipole moment. The rule only requires a change in dipole moment, thus can be a temporary dipole.
| Frequency of Vibration / cm-1 | Infrared absorption intensity |
|---|---|
| 72.72 | 0.0185 |
| 80.14 | 0.1187 |
| 120.01 | 0 |
| 219.76 | 0.1592 |
| 348.85 | 0 |
| 394.29 | 0 |
| 461.68 | 2.8940 |
| 625.67 | 0 |
| 669.40 | 20.0234 |
| 787.80 | 4.0256 |
| 938.19 | 8.9020 |
| 938.65 | 0 |
| 940.12 | 64.7206 |
| 941.79 | 0 |
| 1002.03 | 0 |
| 1033.75 | 0 |
| 1035.98 | 19.7410 |
| 1042.72 | 0 |
| 1067.94 | 9.5813 |
| 1203.21 | 0 |
| 1250.95 | 0.5904 |
| 1288.84 | 6.4705 |
| 1323.03 | 0 |
| 1339.07 | 0 |
| 1343.14 | 1.3918 |
| 1384.10 | 0 |
| 1473.71 | 0 |
| 1476.22 | 1.5099 |
| 1508.56 | 0 |
| 1523.21 | 5.6212 |
| 1730.95 | 0 |
| 1734.24 | 18.1433 |
| 3021.69 | 0 |
| 3031.33 | 53.6390 |
| 3060.30 | 0 |
| 3080.32 | 35.8433 |
| 3135.92 | 0 |
| 3136.98 | 56.0529 |
| 3155.47 | 14.7174 |
| 3155.73 | 0 |
| 3233.89 | 0 |
| 3233.92 | 45.4813 |
As seen in the table above, a lot of vibrational modes have an infrared absorption intensity of zero and also, does not show up in the IR spectrum above. This is due the high symmetry (Ci)of the anti2 1,5-hexadiene leading to many vibrations that do not generate a dipole moment, thus are IR-inactive.
Thermochemistry
Sum of electronic and zero-point Energies= -234.469212 Sum of electronic and thermal Energies= -234.461856 Sum of electronic and thermal Enthalpies= -234.460912 Sum of electronic and thermal Free Energies= -234.500822
Optimizing the "Chair" and "Boat" Transition Structures of Cope Rearrangement
Optimising the transition state structures are a much more complex process as compared to optimising the reactants and products. This is because in order for calculation to be accurate, Gaussian needs to know which direction of curvature is the negative one, and it can do so by computing a force constant matrix also known as the Hessian. This calculation method however requires the guess transition state structure to be close enough to the actual transition state structure. If not, the curvature obtained at that particular surface may be significantly different from that of the actual surface. For 1,5-hexadiene, optimising the transition state involves forming and breaking of a bond and can go via a chair transition state or a boat transition state. By optimising to a chair and boat transition state and comparing the relative energies, we can determine which is the transition state stucture that is lowest energy transition state. The Cope rearrangement is a kinetic process, thus the reaction will proceed via the lowest transition state.
Optimizing Allyl Fragment CH2CHCH2
The first step of optimising the chair transition state would be optimisation of a half of the hexadiene - an allyl fragment.
Method: Hartree Fock
Basis Set: 3-21g
| Allyl Fragment CH2CHCH2 | |
|---|---|
| File type | .log |
| Calculation Type | FOPT |
| Calculation Method | UHF |
| Basis Set | 3-21G |
| Final energy in atomic units (au) | -115.82304009 |
| Gradient | 0.00003730 au |
| Dipole Moment | 0.0292 Debye |
| Point Group | C1 |
| Calculation Time Taken | 0 min 32 sec |
Link: File:Allyl Fragment.log
Symmetry : C2V
Item Value Threshold Converged?
Maximum Force 0.000089 0.000450 YES
RMS Force 0.000028 0.000300 YES
Maximum Displacement 0.000360 0.001800 YES
RMS Displacement 0.000148 0.001200 YES
Predicted change in Energy=-2.381053D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.0757 -DE/DX = -0.0001 !
! R2 R(2,3) 1.3885 -DE/DX = 0.0001 !
! R3 R(2,6) 1.3885 -DE/DX = 0.0001 !
! R4 R(3,4) 1.0722 -DE/DX = 0.0 !
! R5 R(3,5) 1.074 -DE/DX = 0.0 !
! R6 R(6,7) 1.074 -DE/DX = 0.0 !
! R7 R(6,8) 1.0722 -DE/DX = 0.0 !
! A1 A(1,2,3) 117.8547 -DE/DX = 0.0 !
! A2 A(1,2,6) 117.855 -DE/DX = 0.0 !
! A3 A(3,2,6) 124.2903 -DE/DX = 0.0 !
! A4 A(2,3,4) 121.4189 -DE/DX = 0.0 !
! A5 A(2,3,5) 121.1232 -DE/DX = 0.0 !
! A6 A(4,3,5) 117.4579 -DE/DX = 0.0 !
! A7 A(2,6,7) 121.1214 -DE/DX = 0.0 !
! A8 A(2,6,8) 121.4209 -DE/DX = 0.0 !
! A9 A(7,6,8) 117.4578 -DE/DX = 0.0 !
! D1 D(1,2,3,4) 0.0 -DE/DX = 0.0 !
! D2 D(1,2,3,5) -180.0 -DE/DX = 0.0 !
! D3 D(6,2,3,4) 180.0 -DE/DX = 0.0 !
! D4 D(6,2,3,5) 0.0 -DE/DX = 0.0 !
! D5 D(1,2,6,7) 180.0 -DE/DX = 0.0 !
! D6 D(1,2,6,8) 0.0 -DE/DX = 0.0 !
! D7 D(3,2,6,7) 0.0 -DE/DX = 0.0 !
! D8 D(3,2,6,8) -180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
The optimisation was successful as convergence to a minimum was achieved.
Optimizing and Frequency Analysis of Chair TS
Following the optimisation of an allyl fragment, the optimized fragment was copied twice into a separate molecule window and oriented to resemble the chair transition state in Appendix 2.
Basis Set: 3-21G
| Chair Transition State | |
|---|---|
| File type | .log |
| Calculation Type | FREQ |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Final energy in atomic units (au) | -231.61932239 |
| Gradient | 0.00003282 au |
| Dipole Moment | 0.0002 Debye |
| Point Group | Ci |
| Calculation Time Taken | 0 min 13 sec |
Energy of optimised compound = -231.61932239 au Symmetry : Ci
Item Value Threshold Converged?
Maximum Force 0.000042 0.000450 YES
RMS Force 0.000007 0.000300 YES
Maximum Displacement 0.001299 0.001800 YES
RMS Displacement 0.000147 0.001200 YES
Predicted change in Energy=-8.939592D-08
Optimization completed.
-- Stationary point found.
Low frequencies --- -817.8876 -4.9327 -2.1079 -0.0006 -0.0004 0.0002
Low frequencies --- 4.8688 209.5842 396.0987
The optimisation was successful as convergence to a transition state was achieved. One of the low frequencies obtained is an imaginary frequency at -817.8876 cm-1, which is indicative of a transition state. Upon animation, we observe that the vibration corresponds to the Cope rearrangement, via a chair transition state.
Redundant Coordinate Method of Optimisation
Another method of optimisation of transition state involves the use of a redundant coordinate parameter. This allows us to freeze the reactive centres and hence minimize the rest of the molecule first. Subsequently, the reactive centres are unfrozen and optimized with the rest of the molecule already at the minimum. This often gives a more accurate determination of the transition state optimum.
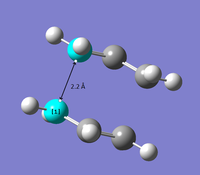
The same guess structure used in the previous part was used as a starting point and the freeze bond setting was applied to the atoms where bonds are formed via the Edit-->Reduntant Coordinates function. Bond angles could be set by clicking on the Modify bond tool in Gaussview. It could also be set by opening the source file of the input file and adding the line B 5 1 2.2 B as follows:
# opt=modredundant hf/3-21g geom=connectivity chair_redundantcoord_opt 0 1 H -0.66453632 -0.95596654 0.02282130 C 0.16493709 0.24828195 1.55946699 H -0.15623149 1.16872620 1.10416522 H 0.31899234 0.31979573 2.62024283 C 0.15890254 -2.16405336 1.55952069 H 0.31297285 -2.23629359 2.62019230 H -0.16733038 -3.08276068 1.10410851 C -0.27336372 -0.95691982 1.02501257 H 3.11613426 -0.96491980 2.53704339 C 2.28666084 -2.16916829 1.00039771 H 2.60782942 -3.08961254 1.45569948 H 2.13260560 -2.24068207 -0.06037814 C 2.29269540 0.24316702 1.00034400 H 2.13862509 0.31540725 -0.06032760 H 2.61892832 1.16187434 1.45575618 C 2.72496165 -0.96396652 1.53485212 1 8 1.0 2 3 1.0 4 1.0 8 1.5 3 4 5 6 1.0 7 1.0 8 1.5 6 7 8 9 16 1.0 10 11 1.0 12 1.0 16 1.5 11 12 13 14 1.0 15 1.0 16 1.5 14 15 16 B 2 13 F B 2 13 2.2 B B 5 10 F B 5 10 2.2 B
Thereafter, the guess structure is optimised to a minimum using the same basis set as before and a similar optimised structure is obtained except that the bond lengths between the bonds that are supposed to form are fixed are 2.2 Å.
Method: Hartree Fock
Basis Set: 3-21G
| Chair Optimisation (Freeze Bond) | |
|---|---|
| File type | .log |
| Calculation Type | FOPT |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Final energy in atomic units (au) | -231.61518450 |
| Gradient | 0.00324925 au |
| Dipole Moment | 0.0000 Debye |
| Point Group | C1 |
| Calculation Time Taken | 0 min 12 sec |
Symmetry: C2h
Link:Media:CHAIR REDUNDANTCOORD OPT.LOG
Item Value Threshold Converged?
Maximum Force 0.000039 0.000450 YES
RMS Force 0.000013 0.000300 YES
Maximum Displacement 0.001587 0.001800 YES
RMS Displacement 0.000416 0.001200 YES
Predicted change in Energy=-6.425287D-07
Optimization completed.
-- Stationary point found.
The optimisation was successful as convergence to a transition state was achieved. However energy obtained was slightly higher at -231.61518450 au compared to -231.61932239 au obtained for the previous optimisation. This is due to the frozen bonds that are not at their optimum bond lengths. The rest of the molecule is nonetheless optimised to their minimum. The molecule can now be unfrozen at the reaction centres and optimized again, this time to a transition state and not a minimum.
Unfreezing the frozen bonds
The output file with frozen bonds is copied into a new molecule window and the frozen bonds are now unfrozen by changing the redundant coordinates to Bond Derivative, which utilises the Hessian. The optimisation set up involved the following set-up:
Job type: Opt+Freq
Optimize to a: TS (berny)
Calculate Force Constants: Never
Keywords: opt=(noeigen, catesian)
Method: Hartree Fock
Basis Set: 3-21g
| Unfrozen Optimisation | |
|---|---|
| File type | .log |
| Calculation Type | FREQ |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Final energy in atomic units (au) | -231.61932228 |
| Gradient | 0.00003916 au |
| Dipole Moment | 0.0000 Debye |
| Point Group | C1 |
| Calculation Time Taken | 0 min 7 sec |
Link: Media:Chair derivative opt.out
Symmetry : Ci
Item Value Threshold Converged?
Maximum Force 0.000100 0.000450 YES
RMS Force 0.000039 0.000300 YES
Maximum Displacement 0.000760 0.001800 YES
RMS Displacement 0.000370 0.001200 YES
Predicted change in Energy=-1.935288D-07
Optimization completed.
-- Stationary point found.
The optimisation was successful as convergence to a transition state was achieved. However energy obtained was -231.61932228 au, lower than the -231.61518450 au obtained for the frozen bond optimisation, which was expected and comparable to -231.61932239 au obtained for the previous optimisation without using the redundant coordinate method.
The bond forming/bond breaking bond lengths of the optimisations are both at 2.02 Å. As such, we can conclude both methods (with or without redundant coordinate) are reasonable transition state optimisation methods as long as the guess structure at the beginning is good enough, which remains the most crucial part of transition state optimisation.
A similar imaginary vibration is also obtained for this optimisation at -817.85 cm-1, indicative of a transition state. Upon animation, we observe that the vibration corresponds to the Cope rearrangement, via a chair transition state.
Optimizing and Frequency Analysis of Boat TS
The boat transition state is obtained by a very different method from the chair transition state. A method called QST2 is employed.
Failed Attempt: Wrong reactant/product geometry
Firstly, the optmised anti2 1,5-hexadiene (the reactant molecule) is opened and copied and pasted into a new molecule screen. A 2nd molecule is pasted in the same MolGroup, that allows it to be displayed side-by-side in the same molecule screen as follows. The numberings on the C & H atoms are also rearranged such that the molecule on the right tab is a Cope-rearrangement product of that in the left tab. This rearrangement can be done by editing the Atom List parameters in a running order from atom 16-1.
Upon rearrangement, a QST2 calculation can be set up using the following set-up details:
Job type: Opt+Freq
Optimize to a: TS(QST2)
Calculate Force Constant: Never
Method: Hartree Fock
Basis Set: 3-21G
| Boat Optimisation (QST2 -- failed) | |
|---|---|
| File type | .log |
| Calculation Type | FREQ |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Final energy in atomic units (au) | -231.61932234 |
| Gradient | 0.00004373 au |
| Dipole Moment | 0.0002 Debye |
| Point Group | C1 |
| Calculation Time Taken | 0 min 8 sec |
Symmetry: Ci
This optimisation is however failed as the output generated is a chair optimisation geometry and the chk file shows that the bonds forming on the respective ends have crossed one another so that the boat structure is converted over to the chair. Thus, though convergence was achieved, it had gone through a different transtion state (i.e. chair instead of boat)
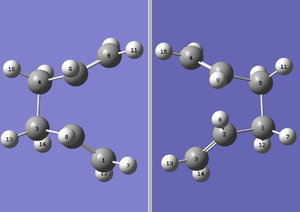
Successful Attempt: Modified reactant/product geometry
The failure is due to the starting geometry of anti2 hexadiene being a wrong starting point for the optimisation. Thus, a more accurate geometry is required for the reactant and product molecules is required. This can be done by rotating the central C-C-C-C dihedral angle of 1,5-hexadiene from 180o to 0o, changing the inside C-C-C angle of C2-C3-C4 and C3-C4-C5 of the reactant molecule and reduce them to 100o. The same is done to the product molecule and they should end up like the screenshot below. The hydrogen groups will also need to be adjusted so that they are in the correct orientations and are numbered correctly with respect to the attached carbon.
Upon realigning of geometry, the new product and reactant molecules can be optimised via the same method and the correct boat transtion state should be attained.
Method: Hartree Fock
Basis Set: 3-21G
| Boat Optimisation (QST2) | |
|---|---|
| File type | .log |
| Calculation Type | FREQ |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Final energy in atomic units (au) | -231.60280212 |
| Gradient | 0.00003958 au |
| Dipole Moment | 0.1585 Debye |
| Point Group | C1 |
| Calculation Time Taken | 0 min 9 sec |
Symmetry: C2V
Item Value Threshold Converged?
Maximum Force 0.000067 0.000450 YES
RMS Force 0.000022 0.000300 YES
Maximum Displacement 0.000974 0.001800 YES
RMS Displacement 0.000275 0.001200 YES
Predicted change in Energy=-1.185167D-07
Optimization completed.
-- Stationary point found.
Convergence has been achieved.
Low frequencies --- -840.2505 -3.5563 -2.9068 0.0004 0.0005 0.0006 Low frequencies --- 5.8078 155.3524 382.3394 ****** 1 imaginary frequencies (negative Signs) ******
There is also 1 imaginary vibration obtained at frequency -840.2505 cm-1, indicative of a transition state. Display of vibrations showed that the imaginary frequency at -840.2505 cm-1 corresponds to the Cope-rearrangement, proceeding via a boat transition state.
QST2 method has proven to be useful as it is a fully automated process but it often fails if the reactant and products are not close to the transition structure as seen in the case of the original anti2 1,5-hexadiene.
IRC Analysis
In order to predict the conformer that the transition structure will lead to eventually, we need to monitor the reaction pathway and this can be done by using the Intrinsic Reaction Coordinates (IRC) method that allows the following of the minimum energy path from the transition structure down to its local minimum. It creates a series of points by taking small geometry steps in the direction where the gradient is the steepest, leading to either the final product or reactant.
Due to the symmetry of the reaction coordinates in the Cope rearrangement, we could just observe the IRC coordinate in the forward direction.
IRC Analysis (Chair TS)
The IRC is set up as follows:
Job type: IRC Follow IRC: Forward Only Force Constants: Calculate Always Compute more points, N = 50
Method: Hartree-Fock Basis-Set: 3-21G
The IRC above shows that the chair transition state leads to a gauche conformer of product 1,5-hexadiene. However, the last point of the IRC is often not the minimum and needs further optimisation to a minimum such that the low energy conformer can be determined.
An optimisation to a minimum is set up as follows:
Method: Hartree-Fock Basis-Set: 3-21G
| Optimisation (Last point IRC -- Chair TS) | |
|---|---|
| File type | .log |
| Calculation Type | FOPT |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Final energy in atomic units (au) | -231.69166702 |
| Gradient | 0.00000474 au |
| Dipole Moment | 0.3806 Debye |
| Point Group | C2 |
| Calculation Time Taken | 0 min 12 sec |
Symmetry: C2
Item Value Threshold Converged?
Maximum Force 0.000010 0.000450 YES
RMS Force 0.000003 0.000300 YES
Maximum Displacement 0.000300 0.001800 YES
RMS Displacement 0.000091 0.001200 YES
Predicted change in Energy=-2.405616D-09
Optimization completed.
-- Stationary point found.
Convergence has been achieved in this optimisation and the final energy (-231.69166702 au) and geometry (C2) obtained corresponds to the gauche2 low energy conformer from Appendix 1.
IRC Analysis (Boat TS)
The IRC is set up as follows:
Job type: IRC Follow IRC: Forward Only Force Constants: Calculate Always Compute more points, N = 100 -- A higher N is inserted for this calculation to get a better minimum at the end of the IRC run.
Method: Hartree-Fock Basis-Set: 3-21G
The IRC above shows that the boat transition state leads to another gauche conformer of product 1,5-hexadiene. However, as with the previous IRC run, the last point of the IRC is often not the minimum and needs further optimisation to a minimum such that the low energy conformer can be determined.
An optimisation to a minimum is set up as follows:
Method: Hartree-Fock Basis-Set: 3-21G
| Optimisation (Last point IRC -- Boat TS) | |
|---|---|
| File type | .log |
| Calculation Type | FOPT |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Final energy in atomic units (au) | -231.69266120 |
| Gradient | 0.000001184 au |
| Dipole Moment | 0.3407 Debye |
| Point Group | C1 |
| Calculation Time Taken | 0 min 18 sec |
Symmetry: C1
Link:Media:IRC BOAT LASTPTMIN.LOG
Item Value Threshold Converged?
Maximum Force 0.000031 0.000450 YES
RMS Force 0.000009 0.000300 YES
Maximum Displacement 0.001402 0.001800 YES
RMS Displacement 0.000284 0.001200 YES
Predicted change in Energy=-1.955451D-08
Optimization completed.
-- Stationary point found.
Convergence has been achieved in this optimisation and the final energy (-231.69266120 au) and geometry (C1) obtained corresponds to the gauche3 low energy conformer from Appendix 1. The gauche3 low energy conformer of 1,5-hexadiene is the lowest energy conformer.
Re-optimisation of TS using higher basis set
In order to calculate activation energies of the different transition states, we need a more accurate optimisation of the transition states. A higher basis set is now used to improve the accuracy. Geometries obtained for both the chair and boat transition states are unchanged but energy levels have been lowered significantly in both cases.
Re-optimisation of TS using higher basis set (CHAIR TS)
A previously optimised Chair TS was chosen and used in this re-optimisation. The re-optimisation set-up is as follows:
Job type: Opt+Freq
Optimize to a: TS(QST2)
Calculate Force Constant: Never
Method: DFT/B3LYP
Basis Set: 6-31Gd
| Reoptimisation (chair TS) | |
|---|---|
| File type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d) |
| Final energy in atomic units (au) | -234.55698286 |
| Gradient | 0.00004909 au |
| Dipole Moment | 0.0000 Debye |
| Point Group | C1 |
| Calculation Time Taken | 2 min 54 sec |
Symmetry: C2v
Link: Media:CHAIR TS 631GD.LOG
Item Value Threshold Converged?
Maximum Force 0.000116 0.000450 YES
RMS Force 0.000049 0.000300 YES
Maximum Displacement 0.001543 0.001800 YES
RMS Displacement 0.000640 0.001200 YES
Predicted change in Energy=-3.220993D-07
Optimization completed.
-- Stationary point found.
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Convergence is achieved and the transition state energy level obtained using this basis set has lowered rather significantly.
Thermochemistry
Sum of electronic and zero-point Energies= -234.414927 Sum of electronic and thermal Energies= -234.409006 Sum of electronic and thermal Enthalpies= -234.408062 Sum of electronic and thermal Free Energies= -234.443812
Re-optimisation of TS using higher basis set (BOAT TS)
A previously optimised Boat TS was chosen and used in this re-optimisation. The re-optimisation set-up is as follows:
Job type: Opt+Freq
Optimize to a: TS(QST2)
Calculate Force Constant: Never
Method: DFT/B3LYP
Basis Set: 6-31Gd
| Reoptimisation (boat TS) | |
|---|---|
| File type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d) |
| Final energy in atomic units (au) | -234.54309307 |
| Gradient | 0.00000409 au |
| Dipole Moment | 0.0613 Debye |
| Point Group | C1 |
| Calculation Time Taken | 8 min 36 sec |
Symmetry: C2
Link: Media:BOAT TS 631GD.LOG
Item Value Threshold Converged?
Maximum Force 0.000009 0.000450 YES
RMS Force 0.000003 0.000300 YES
Maximum Displacement 0.000148 0.001800 YES
RMS Displacement 0.000053 0.001200 YES
Predicted change in Energy=-2.755574D-09
Optimization completed.
-- Stationary point found.
Convergence is achieved and the transition state energy level obtained using this basis set has lowered rather significantly.
Thermochemistry
Sum of electronic and zero-point Energies= -234.402342 Sum of electronic and thermal Energies= -234.396008 Sum of electronic and thermal Enthalpies= -234.395063 Sum of electronic and thermal Free Energies= -234.431752
Thermochemical Analysis
Summary of energies
| B3LYP/6-31G* | |||
|---|---|---|---|
| Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | |
| at 0 K | at 298.15 K | ||
| Chair TS | -234.556983 | -234.414927 | -234.409006 |
| Boat TS | -234.543093 | -234.402342 | -234.396008 |
| Reactant (anti2) | -234.611703 | -234.469212 | -234.461856 |
*1 a.u. = 627.509 kcal/mol
Activation energies (in kcal/mol)
| B3LYP/6-31G* | B3LYP/6-31G* | Expt. | |
| at 0 K | at 298.15 K | at 0 K | |
| ΔE (Chair) | 34.06 | 33.16 | 33.5 ± 0.5 |
| ΔE (Boat) | 41.96 | 41.32 | 44.7 ± 2.0 |
The activation energies obtained from the 6-31G(d) basis set is quite close to the energies obtained via experiment. Therefore, it can be determined that the basis set is good enough for thermodynamic analysis. The activation energy of the energy pathway going through the boat transition state also gives a higher ΔE compared to the chair. This is expected as the boat structure is a less stable transition state compared to the corresponding chair structure. Given that the 3-21G basis set differs from the 6-31G(d) basis set quite significantly, it is likely to be highly inaccurate in the determination of ΔE.
Week 2
Diels-Alder: Cyclohexene
The formation of cyclohexene involves the most basic Diels-Alder cycloaddition of cisbutadiene and ethene. By optimising the transition state of the reaction, we are able to follow the reaction pathway and determine the symmetric properties of the HOMO and LUMO.
Optimisation of cis-butadiene
Cis-butadiene was optimised via the following setup:
Job-Type: Opt+Freq
Optimise to a: Minimum
Calculate force Constants: Never
Method: Semi-empirical/AM1
| cis-butadiene Optimisation | |
|---|---|
| File type | .log |
| Calculation Type | FREQ |
| Calculation Method | RAM1 |
| Basis Set | ZDO |
| Final energy in atomic units (au) | 0.04879734 |
| Gradient | 0.00008900 au |
| Dipole Moment | 0.0414 Debye |
| Point Group | C2 |
| Calculation Time Taken | 0 min 5 sec |
Symmetry: C2v
Item Value Threshold Converged?
Maximum Force 0.000159 0.000450 YES
RMS Force 0.000051 0.000300 YES
Maximum Displacement 0.000783 0.001800 YES
RMS Displacement 0.000254 0.001200 YES
Predicted change in Energy=-1.540844D-07
Optimization completed.
-- Stationary point found.
Convergence has been achieved.
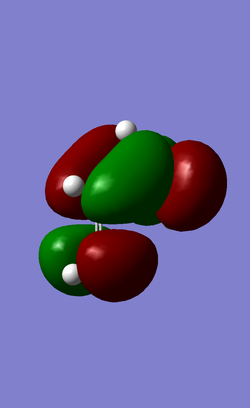
| HOMO | LUMO |
|---|---|

|
|
| AntiSymmetric | Symmetric |
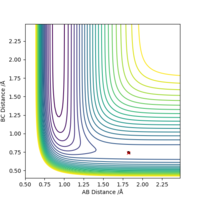
Optimisation of ethylene+cis-butadiene transition state
Ethylene and cis-butadiene transition state can be derived from inserting the guess structure of transition state for their formation of cyclohexene.
Job-Type: Opt+Freq
Optimise to a: TS (Berny)
Calculate force Constants: Once
Keywords: opt=(noeigen)
Method: Semi-empirical/AM1
| Cyclohexene_TS | |
|---|---|
| File type | .log |
| Calculation Type | FREQ |
| Calculation Method | RAM1 |
| Basis Set | ZDO |
| Final energy in atomic units (au) | 0.11165465 |
| Gradient | 0.00000783 au |
| Dipole Moment | 0.5605 Debye |
| Point Group | C1 |
| Calculation Time Taken | 0 min 3 sec |
Symmetry: Cs
Item Value Threshold Converged?
Maximum Force 0.000030 0.000450 YES
RMS Force 0.000005 0.000300 YES
Maximum Displacement 0.000254 0.001800 YES
RMS Displacement 0.000067 0.001200 YES
Predicted change in Energy=-2.398935D-09
Optimization completed.
-- Stationary point found.
Low frequencies --- -956.3610 -0.0527 -0.0240 -0.0032 1.6468 3.1387 Low frequencies --- 3.6666 147.2610 246.6152 ****** 1 imaginary frequencies (negative Signs) ******
Convergence has been achieved. 1 imaginary frequency has been observed at -956.3610 cm-1 indicative of a transition state. An animation of the imaginary vibration below resembles that of a Diels Alder transition state as well. This vibrational illustration also shows that the cycloaddition process is a synchronous one.
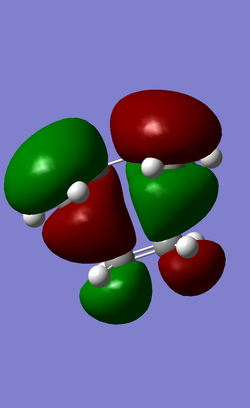
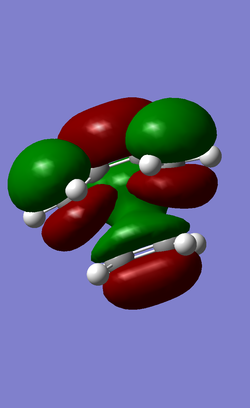
| HOMO | LUMO |
|---|---|
|
|
| AntiSymmetric | Symmetric |
Discussion
The transition state structure shows the geometry of a slightly distorted tetrahedral structure about the bond forming carbons as they are switching from the original sp2 hybridisation to sp3 hybridisation. The ethene molecule approaches the planar cis-butadiene at an angle of 100o, which resembles the Bürgi-Dunitz trajectory, where orbital overlap is maximised.
Bond lengths of the partly formed σ C-C bonds are 2.11920 Å which is longer than a typical sp3 C-C bond length (1.54 Å) or sp2 C=C bond length (1.64 Å). Van der Waals radius of the C atom is 1.70 Å. Therefore, for 2 adjacent C atoms that do not interact, the total radii is 3.40 Å In the partly formed σ C-C bonds, the bond lengths obtained are shorter than the total radii of 2 non-interacting C atoms indicative of attractive forces and orbital overlap between the two carbon atoms, though insufficient to fully form a C-C bond formally.
As mentioned above, the formation of two bonds are synchronous. The lowest positive frequency,in comparison, is found to be at 147.2610 cm-1, which resembles a rocking motion of the ethene molecule and minimal indication with cis-butadiene. It also does not show any indication of any transition state structure. This is expected as positive vibrational frequencies represent a local minimum and not a transition state unlike imaginary frequencies.
The HOMO at the transition structure is antisymmetric. The cycloaddition involves the interaction between HOMO of butadiene (antisymmetric) and LUMO of ethene (antisymmetric) This reaction is allowed as the both butadiene and ethene frontier orbitals have the same antisymmetric property and are relatively close in energy and they are able to match and overlap effectively in space. The closeness in energy would be further enhanced if the ethene LUMO is stabilised by electron-withdrawing groups. The lowering of LUMO energy will allow it to overlap even more effectively with the butadiene HOMO, and result in a lower transition state. This explains why maleic anhydride, with (-C(=O)-O-C(=O)-) attached to ethene component, makes such a good dienophile.
Cyclohexa-1,3-diene with maleic anhydride
The Diels Alder cycloaddition of cyclohexa-1,3-diene with maleic anhydride is more complex than that of cyclohexene as there is the possibility of obtaining either the exo or endo products. This difference arises from the fact that the C-C bonds can be formed from the top face of maleic anhydride (exo) or from the bottom face of maleic anhydride (endo). Theoretically, the endo form goes through a more stable transition state, thus is the preferred kinetic product, though the exo product is the more stable thermodynamic product. This could be proven computationally by examining the relative energies of the exo and endo transition structures.
Optimising the Exo transition state
A guess structure for the exo transition state is constructed to resemble the exo product molecule, with slightly longer bond lengths between the bonding forming carbon atoms (~2.2 Å). The exo transition state of the reaction is optimised via the following set-up:
Job-Type: Opt+Freq
Optimise to a: TS (Berny)
Calculate force Constants: Once
Keywords: Opt=noeigen
Method: Semi-empirical/AM1
| exo TS optimisation | |
|---|---|
| File type | .log |
| Calculation Type | FREQ |
| Calculation Method | RAM1 |
| Basis Set | ZDO |
| Final energy in atomic units (au) | -0.05041979 |
| Gradient | 0.00002406 au |
| Dipole Moment | 5.5647 Debye |
| Point Group | C1 |
| Calculation Time Taken | 0 min 3 sec |
Link: Media:EXO TS 2.LOG
Item Value Threshold Converged?
Maximum Force 0.000101 0.000450 YES
RMS Force 0.000012 0.000300 YES
Maximum Displacement 0.001610 0.001800 YES
RMS Displacement 0.000383 0.001200 YES
Predicted change in Energy=-7.584071D-08
Optimization completed.
-- Stationary point found.
Low frequencies --- -812.2953 -2.4172 -2.0775 -0.4799 -0.0047 0.4370 Low frequencies --- 1.3050 60.7997 123.8552 ****** 1 imaginary frequencies (negative Signs) ******
Converged have been achieved. Frequency analysis gives an imaginary frequency at -812.2953 cm-1, indicative of a transition state. The visualisation of the imaginary frequency shows the suprafacial nature of the concerted cycloaddition.
Symmetry: Cs
Sum of electronic and zero-point Energies= 0.134881 Sum of electronic and thermal Energies= 0.144882 Sum of electronic and thermal Enthalpies= 0.145827 Sum of electronic and thermal Free Energies= 0.099117
Optimising the Endo transition state
The guess structure of the endo transition state is constructed by copying the exo guess structure and rotating the maleic anhydride molecule around such that the -(C=O)-O-(C=O)- fragment lies below the diene component of cyclohexa-1,3-diene.
Job-Type: Opt+Freq
Optimise to a: TS (Berny)
Calculate force Constants: Once
Keywords: Opt=noeigen
Method: Semi-empirical/AM1
| Endo TS | |
|---|---|
| File type | .log |
| Calculation Type | FREQ |
| Calculation Method | RAM1 |
| Basis Set | ZDO |
| Final energy in atomic units (au) | -0.05150480 |
| Gradient | 0.00000684 au |
| Dipole Moment | 6.1660 Debye |
| Point Group | C1 |
| Calculation Time Taken | 0 min 3 sec |
Link: Media:ENDO TS.LOG
Item Value Threshold Converged?
Maximum Force 0.000026 0.000450 YES
RMS Force 0.000003 0.000300 YES
Maximum Displacement 0.000533 0.001800 YES
RMS Displacement 0.000102 0.001200 YES
Predicted change in Energy=-7.799391D-09
Optimization completed.
-- Stationary point found.
Low frequencies --- -806.3619 -1.8701 -1.4257 -0.5415 -0.0104 0.4321 Low frequencies --- 1.1389 62.4149 111.7337 ****** 1 imaginary frequencies (negative Signs) ******
Convergence has been achieved. Frequency analysis shows an imaginary frequency obtained at -806.3619 cm-1, indicative of a transition state. The visualisation of the imaginary frequency shows the suprafacial nature of the concerted cycloaddition.
Sum of electronic and zero-point Energies= 0.133494 Sum of electronic and thermal Energies= 0.143683 Sum of electronic and thermal Enthalpies= 0.144628 Sum of electronic and thermal Free Energies= 0.097350
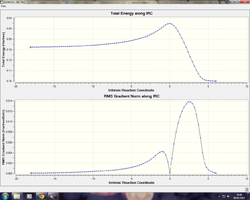
IRC Path of Endo & Exo transition states
IRC analysis was done for both Endo and Exo transition states to follow the reaction pathway from reactions to products.
| IRC (Exo TS) | IRC (Endo TS) |
|---|---|
|
|
|

|
Comparison of Exo/Endo Transition States
Energy Difference
The energy of Exo TS is -0.05041979 au and the energy of Endo TS is -0.05150480 au. Energy difference is therefore 0.00109 au, equivalent to 0.684 kcal/mol. Thus Endo TS is 0.684 kcal/mol more stable than the Endo TS. With addition of zero-point energies, Exo TS has an energy of 0.134881 au while Endo TS has an energy of 0.133494 au. Energy difference is 0.872 kcal/mol, still indicative that endo TS is the more stable one.
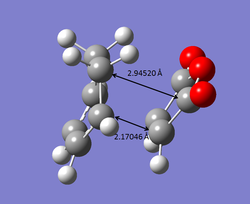
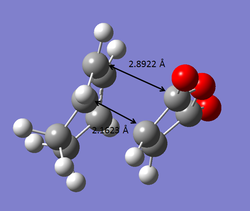
The bond lengths of the endo and exo transition states are also indication of stability of the transition states. The bond forming carbon atoms are slightly closer together at the endo transition state, compared to that at the exo transition state. The presence of secondary orbital overlap effect can also be observed from the bond distance between the non-bonded carbonyl carbons of maleic anhydride and carbons of C=C bond (in endo form) or C-C bond (in exo form).
| EXO TS | ENDO TS |
|---|---|
|
|
MO Analysis of endo and exo form
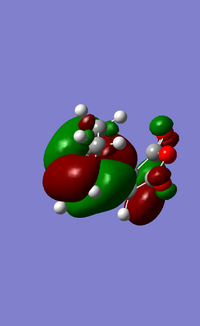
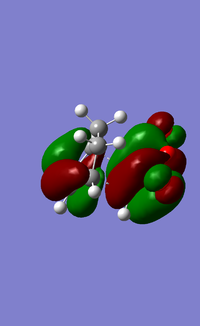
The main structure difference between the endo and exo form is that in the endo form, the electronegative -(C=O)-O-(C=O)- fragment is right underneath the conguated diene component and can can be stabilised by pi-pi interactions (secondary orbital overlap effect) between the groups. There is also secondary orbital overlap effect in the exo form but is a lot less effective overlap is observed. In the exo form, the C-C (unconjugated) fragment is now spatially accessible by the -(C=O)-O-(C=O)- fragment for interaction. However, sp-p interaction is much weaker (minimal) than pi-pi interaction in the endo form. The HOMO/LUMO comparison diagram below illustrates the secondary orbital overlap effects that enhances the stability of endo form over the corresponding exo form.
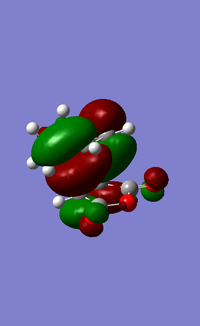
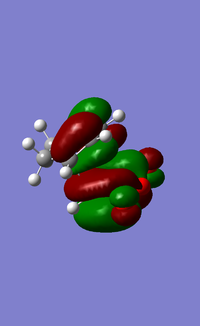
| HOMO (EXO) | LUMO (EXO) | HOMO (ENDO) | LUMO (ENDO) |
|---|---|---|---|
|
|
|
|
When comparing the interaction between -(C=O)-O-(C=O)- fragment and the remainder of the system, we can observe nodal lobes present around each O atom for both the exo and endo HOMOs. The size of the nodal area between the fragment and the remainder of the system also indicates the degree of stabilization of the endo orientation compared to the exo one. For the endo transition state, there is a much larger central bonding interaction in the middle (between the diene and dienophile) and a small nodal area. This is indicative of the attractive interaction between the carbons in the O=C-O-C=O fragment and the non bond-forming carbons of the diene component. In contrast, the nodal area between -(C=O)-O-(C=O)- fragment and the remainder of the exo system is large as conjugated diene faces away from the -(C=O)-O-(C=O)- and interaction is impossible.
Conclusion
The Secondary orbital overlap effect is defined as the positive overlap of a non reactive frame in the frontier molecular orbitals of a pericyclic reaction. The effect is crucial in the determination of regiochemistry of the Diels-Alder cycloaddition as evident by thermochemical, bond lengths, and MO analysis done above. They all point to the same conclusion that the endo transition state is the more stabilised one compared to the exo transition state. The overlap effect between the non reactive -(C=O)-O-(C=O)- fragment and the conjugated diene lowers the transition state energy and gives rise to a preferential formation of a kinetic product that resembles the endo transition state.
In these calculations of Diels Alder transition states, some factors that also affect the regiochemistry of the final cycloaddition product have been neglected. Bulky substituents in the dienophile component will usually favour the formation of the exo product over the more sterically crowded endo product. Also, if the Diels Alder reaction is subjected to thermodynamic conditions (i.e. high temperatures over a long period of reaction), the thermodynamic exo product may be preferred over the kinetic product as it is the more stable product.
Although the secondary orbital overlap effect can often effectively control the regiochemistry of the Diels Alder reaction, it bears no sterochemical control at all. Stereochemistry of the Diels Alder cycloaddition is determined instead by the stereochemistry of the starting materials and Diels Alder reaction is typically suprafacial.