Rep:Mod:clras88

Module 2: Transition State

Cope Rearrangement

1,5 Hexadiene Conformers

It should be noted that the symmetrize button was used to determine the point group - the summary box does not display it.

Anti Conformers
Optimisation	Point Group	HF/3-21G Total Energy (kcal/mol)	HF/3-21G Relative Energies (kcal/mol)	B3LYP/6-31G* Total Energy (kcal/mol)	B3LYP/6-31G* Relative Energies (kcal/mol)	Script Conformer
	C2	-145389.1932	0.036859879	-147220.3814	0.628632241	anti1
	Ci	-145389.1511	0.078946907	-147220.9597	0.05037624	anti2
	C2h	-145384.6712	4.558915636	-147221.0101	0.000000000	ant3
	C1	-145388.1692	1.06083534	-147216.6848	4.32526266	anti4
Gauche Conformers
	C2	-145388.6062	0.623856898	-147220.3183	0.691728271	gauche1
	C1	-145389.2301	0.000000000	-147220.7207	0.289425976	gauche3
	C2	-145388.5205	0.709606002	-147220.2123	0.797802392	gauche4

The order of the relative energies of the conformers are clearly effected by the level of calculation applied. Theoretical consideration of the molecule suggests that an anti conformer with respect to the R groups (as shown below) should result in the lowest energy as the most sterically bulky groups are kept furthest apart. Furthermore if the alkene groups in the R groups are orientated away from each other then the dipole moment of the molecule should be lower (more favourable) as well as any potentially destabilising steric clashes. Whilst the a possible gauche effect (σ_C-H→σ*_C-C) could result in lowering the energy of the gauche conformers, it is insufficient (due to the fairly large difference between the two orbitals involved) to overcome destabilising steric clashes of the R groups (separated by 60°). This is due to the difference in energy between the two orbitals interacting being fairly large - stabilisation is inversely proportional to the energy separation of the orbitals interacting.

As shown by the Newman projection view.

Thus the HF suggestion of gauche3 being lowest in energy is flawed. This is most likely due to the fact correlation energies are not taken into account hence more complex many electron interactions are not estimated accurately. The DFT method (more complex interactions taken into account e.g. coulombic) however results in an anti conformer being lowest in energy but does not match the theoretical prediction (anti2). Instead anti1 (C₂) is lowest in energy despite the fact anti1 has a higher dipole moment by 0.2611Debye.

The total energy represents E=E_elec only. Hence when vibrational energies are taken into account the relative order may change. Thus a frequency calculation of the two isomers at the same level (B3LYP/6-31G*) was carried out. From this the E=E_elec+E_vib+E_rot+E_trans values can be compared. When this is done E_Ci=-147126.9242kcal/mol whereas E_C2=-147126.9945kcal/mol. The difference actually increased to 0.070281008kcal/mol. This suggests there are electronic interactions that favour the two alkene groups pointing away from each other on the same face of the molecule or that nuclear energy must also be taken into account into the calculation to obtain support theory. A further reason could be that the error in most computational calculations is greater than 0.01kcal/mol. Even higher level calculations do not re-arrange this order. The MP2/6311++G(d,p) in fact gives a higher difference in the total energy of 0.096975241kcal/mol.

Ci Anti Conformer
Calculation	HF/3-21G	HF/3-21G Script Values	B3LYP/6-31G*
Total Energy (kcal/mol)	-145389.1511	-145389.1541	-147220.9597
Relative Difference (kcal/mol)	1831.80861	1831.80560	0
C-C Length (Å)	1.50887, 1.55294	N/A	1.50423, 1.5481
C=C Length (Å)	1.31614		1.33351
H-C=C-H Angle (°)	0.179		0.389
C-C-C-C Angle (°)	180		179.951

Firstly the comparison of the energy values from the script and calculated values for HF show a high degree of accuracy with very minimal energy difference. This suggests the optimisation was successful. In terms of the difference geometries between the two methods (DFT and HF), the percentage difference is very low (max. ~1.5% except for the H-C=C-H angle). Whilst the HF values are close to theoretical predictions, the DFT values are more accurate to reality since the groups on each atom are not the same and hence perfect bond lengths and angles can not be achieved (different electronic interactions). In spite of this, the data suggests that the calculation level does not significantly affect the geometry.

However if the relative energies are considered, there is far larger difference which can not ignored. Hence an appropriate method for analysis would be to run a lower level HF calculation followed by DFT calculations. The HF calculations are far less time consuming than DFT. However once the most optimum geometry has been approached the DFT calculation time is also reduced resulting in greater computational efficiency.

Energy (Hartree)	E = Eelec	E = Eelec + ZPE	E = Eelec + Evib + Erot + Etrans
HF/3-21G	-231.692535	-231.539540	-231.532566
B3LYP/6-31G*	-234.611710	-234.469204	-234.461857

Once more the vibrational analysis has provided data that matches the script values to an accuracy of >99%. Hence the calculation has clearly been successful. Calculation of the energies at 0K exactly is not possible due to the entering 0 resulting in the default setting of 298.15K being applied. Hence instead a value of 0.00001K was used on the FreqChk utility on Gaussian03W program. This showed no difference in energy between the thermal and electronic energy (and zero point energy) as expected since there is no kinetic energy available for translational, vibrational and rotational energy.

Transition States

All transition states can clearly be identified by the presence of an imaginary negative vibration which corresponds to the pathway of the reaction when animated. This was the criteria applied to all T.S. optimisation and frequency calculations to check the structure is in fact a T.S. The chair T.S. was composed of CH₂CHCH₂ fragments optimised separately before T.S. optimisation at the HF/3-21G level.

HF/3-21G
3D	Pentahelicene		Pentahelicene
Method	T.S. (Berny)	Redundant Co-ord.	QST2	QST3
Total Energy (kcal/mol)	-145343.2093	-145343.2094	-145332.8427	-145332.8428
E = Eelec (Hartree)	-231.619322		-231.602802
E = Eelec + ZPE (Hartree)	-231.466701		-231.450928
E = Eelec + Erot + Evib + Etrans (Hartree)	-231.461341		-231.445299
Frequency (cm-1)	-817.862	-817.913	-840.151	-839.711
Intensity	5.8610	5.8548	1.6184	1.5991
C---C Bond Forming/Breaking Length (Å)	2.02044, 2.02042	2.02054, 2.02056	2.14009, 2.13954	2.14075, 2.14026
C-C Length (Å)	1.38928, 1.38921, 1.38934	1.38928, 1.38924	1.38153, 1.38144, 1.38149, 1.38146	1.38138, 1.38132, 1.38142
C-C-C Angle (°)	120.496	120.502	121.655, 121.700	121.676, 121.708

The transition states shown above were calculated as described in the script. The additional text of opt=noeigen was used in all calculations for the T.S. as without it the error message 2070 was encountered more frequently.

Comparison of the TS(Berny) and the redundant co-ordinates methods show the fact there is little to no difference between them in terms of energy. However the geometries of the two chair T.S.s show a small difference (<1% difference). This is due to the structure being optimised prior to the transition state being evaluated. This causes greater accuracy in the geometry which can be important if that degree of accuracy is desired. However if the T.S. is already known to be closer in energy to the reactants (exothermic reaction) or the products (endothermic reaction), then based on Hammond's postulate the T.S. does not need significant rearrangement and hence the T.S.(Berny) method is sufficiently adequate. It should be noted that in all calculations run in the module and C-C bond forming/breaking distances were guessed to be ~2.2Å (as indicated by the script and confirmed by calculation of the T.S.).

Comparison of the qst2 and qst3 methods for the boat T.S. show a similar trend to the above comparison i.e. there is very little difference in the energies. The geometry also shows the same percentage difference (<1%). The qst3 method offers greater accuracy since the transition state can be guessed separately and the reactant and product molecules do not have to be altered to approach the transition state geometry. Hence in terms of accuracy and efficiency the qst3 method appears more suitable. Both of these methods are however far more time consuming to apply than the methods used for the chair T.S. since the atomic numbering has to the exact same - a complex task for larger molecules. Thus all further transition state calculations are run using the redundant co-ordinates method since this is most is the safest method, despite being slightly longer than T.S.(Berny), to evaluate the T.S.

The geometries of the transition state itself it appears to conform to a synchronous bond formation since the difference between the two different bond forming/breaking lengths are negligible. The C-C lengths are also in keeping with a bond order of approximately 1.4 (the bond length is closer to a C=C bond [1.330Å] than a C-C bond [1.540Å]).

Intrinsic Reaction Co-ordinates

Chair T.S.
Method	N=50, Force=Once	N=50, Force=Once, Minimisation (HF/2-31G)	N=50, Force=Always	N=100, Force=Once
I.R.C.		N/A
Total Energy (kcal/mol)	-145381.6415	-145388.6063	-145356.1214	-145387.9322

I.R.C. results in the formation of the reactants or products from the T.S. This calculation itself is quite demanding even at the HF level none of the IRCs have reached a 0 gradient and thus a minimised energy for the reactant (which in this case is the same as the product). The higher number of point, the closer to the minimum energy geometry (N=100). However the calculation can take ~7hrs. The force constant always option should return more accurate results but the calculation time is too high. Error 9999 was reached and only 14 sets were shown. Hence the maxcycles must be raised. The minimisation of the final structure in the N=50 run results in the lowest energy being obtained.

However upon comparison of this value with the reactant anti2 (calc. value = -145389.1511kcal/mol), it can be seen the energies do not match up (difference of 0.5448kcal/mol). This is due to the IRC not causing rotation around the C³-C⁴ bond as illustrated in the Newman projections earlier. Hence the IRC minimisations must be treated with caution. Thus to gain the greatest accuracy and most data for evaluation (e.g. thermochemistry data), running a minimisation of the final point in the a N=100 I.R.C. appears most efficient and shall be used in the following I.R.C.s.

Activation Energy

Method	HF/3-21G		B3LYP/6-31G*		Experimental
Temperature (K)	0	298.15	0	298.15	298.15
Chair Activation Energy (kcal/mol)	45.71	44.69	34.06	33.16	33.5 ± 0.5
Boat Activation Energy (kcal/mol)	55.60	54.76	41.96	41.32	44.7 ± 2.0

The values provided by the script and calculated are in very good agreement suggesting the calculation has been done. On comparison to lit. values provided in the script, it can be seen that computational methods are fairly accurate as the values are within the error range of the lit except for the boat transition state.

The boat value, however is not. This could be due to the reaction profile of reaction. It should be noted that the conformer chosen as the reactant and product (anti2) does not appear to be orientated in such a way to facilitate easy access to the transition state. This is obvious from the qst2 alterations required to achieve a T.S.esque structure. Hence the actual reaction profile could be more complex:-

From the above diagram it can be seen that the potentially the anti2 conformer 1 may require sufficient activation energy to overcome an initial ΔE_{interconversion} barrier to a more favourable conformer 2 before the reaction can proceed to the transition state (ΔE_ACT) and back to conformer 1. Hence a greater amount of energy is required than predicted by computational methods. The ΔE_{interconversion} is most likely very accessible since the relative energies between 1,5-hexadiene conformers is no greater than 1kcal/mol. This value is also a typical error associated with computational analysis methods.

A further problem with the calculation of activation energies is that the reactant conformer 1 may not be the same conformer as the product conformer which could be a lower energy conformer 3 (anti1 for example). Hence for more complex reaction where the energy differences are greater this problem should be carefully considered when working out reaction (ΔE_REACT) or activation energies (ΔE_ACT).

Diels-Alder Reaction

Cis-Butadiene

The molecule was initially optimised using HF/3-21G followed by a higher level B3LYP/6-31G* optimisation.

3D	HOMO	LUMO
Pentahelicene

The above pictures clearly show that the cis-butadiene is not planar as expected from theory. The MOs nonetheless still show π bonds indicating that a perfect planar arrangement is not always required. Although better overlap would result in stronger double bonds, the molecule must be considered as a whole. Computational methods try and minimise the energy of the entire molecule not just a specific molecular orbital. Hence this deviation from planar arrangement of p orbitals must be offset by a stabilisation of other molecular orbitals.

Cyclohexene Transition State

The following calculations were obtained from an optimisation and frequency calculation initially at HF/3-21G then B3LYP/6-31G* followed finally by MP2/6-31G* (for comparison purposes to lit. and because correlation effects are taken into account). All data is from the MP2 level.

3D	HOMO-1	HOMO	LUMO
Pentahelicene
Negative Vibration (-516.22cm-1, 9.8036 Intensity)		First Positive Vibration (133.631cm-1, 0.6393 Intensity)
Total Energy (Hartree)		-233.679105
C---C Bond Forming Length (Å)		2.28524
C-C (Ethene) Length (Å)		1.38213
C-C (cis-butadiene) Length (Å)		1.41161, 1.38015
H-C=C-H (cis-butadiene) Angle (°)		8.121

The optimisation appears successful with lit. C---C bond forming distance of 2.285Å. This is further supported by comparison of the C-C with lit. values for C-C [from diamond 1.540Å] and C=C [from ethene 1.330Å]. The calc. C-C bonds where double bonds originally reside in the reactants are slightly longer than lit. values whilst the single C-C bond is also shorter. This is indicative of the bond positions changing as the C=C bonds become single bonds and the C-C bond becomes a double bond. The C-C bond is far smaller in length than lit. and this may be due to the hybridisation of the two C centres where this bond is located - they are both sp² and hence already have pronounced s character which would shorten the bond length from a typical diamond C-C bond length. Furthermore the H-C=C-H angle is no longer 0° suggesting that the orbitals have been realigned to adopt a more stable conformation for the T.S.

If the van der Waals' Radius of C is considered (1.681Å), it can be seen that the there is already considerable overlap. From the nucleus of 1 C atom to the other C atom, if there are no interactions but the atoms are in contact the length would be 3.362Å. The bond forming distances are however 2.28524Å. Thus there is considerable overlap of orbitals from the two C atoms. The bond forming distance is only 48% greater than a C-C sp³ bond.

Electron rich diene and electron deficient ethene

The HOMO is clearly antisymmetric with respect to the plane as expected from a HOMO - LUMO interaction between the cis-butadiene and ethene respectively (there is a node at the plane - indicative of allowed reactions). Hence this reaction proceeds via a favourable 4n+2 aromatic transition state (n=1) with only one bond forming length and not two. This implies the bonds are formed synchronously. The negative imaginary vibration clearly indicates the reaction pathway whilst the first positive value shows no such movement. This implies that the positive frequencies have no effect or show no link to the transition state pathway. This reaction is allowed due to good orbital overlap of the HOMO resulting in electron density at the positions bonds form between the two reactants.

An interesting point to note is that at the lower level calculations (HF and B3LYP) the HOMO and the HOMO-1 are actually reversed in order. This is due to the point made in the cis-butadiene section. The MOs are minimised in energy as a whole and not separately. To check that theory works in these situations the MOs approaching the transition state can be visualised to see if the pathway to the T.S. follows theory. This could be done via an I.R.C. and taking points along the reaction co-ordinates from the reactant or product to T.S. This was not necessary in this case due to the MP2 level calculations yielding results agree with theory.

Endo/Exo Transition States

The T.S. was initially ran on a optimisation and frequency calculation at HF/3-21G before using a higher level B3LYP/6-21G* calculation. All results presented in this section are from the higher level calculation.

T.S.	Endo	Exo
3D	Pentahelicene	Pentahelicene
Total Energy (kcal/mol)	-384464.3456	-384461.7817
Relative Energy (kcal/mol)	0.0000	2.5639
HOMO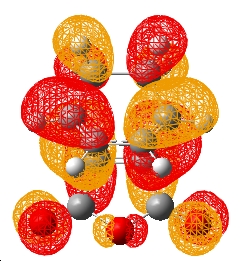
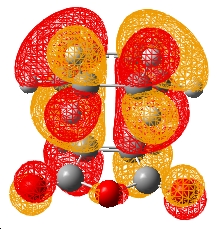
Bond Lengths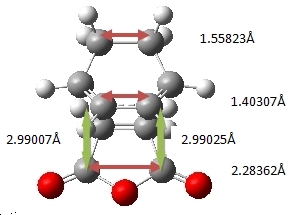
Bond Forming Distances (Å)	2.26831	2.29023

IRC for T.S.→reactants

It should be noted that prior to the analysis, the MP2 level calculation may yield more accurate results since electron correlations are taken into account which is not done by the B3LYP method. Hence with more time this level calculation should be preformed.

As it can be seen the HOMOs of both T.S.s are antisymmetric with respect to the plane. Hence the reactions are allowed as stated in the cyclohexene Diels-Alder reaction (the bond forming lengths also indicate a synchronous bond formation). However the endo form does not exhibit any form of secondary orbital overlap. The orbitals of the anhydride show no interaction with the diene orbitals. This is also the case when the orbitals are considered of the states leading to the T.S. From the IRC a point close to the reactants (point 80) and a point close to the transition state (point 13) were optimised on a energy calculation at B3LYP/6-31G*. These HOMOs at these energies did not show a secondary orbital interaction. Hence the endo conformer must be lower in energy for other reactions - sterics.

If the exo structure is considered it can be seen that the C-C distance opposite the C=O-CO-C=O is similar in length. Furthermore the C centres on the diene are sp³ hybridised. Hence there is greater steric interactions between the H atoms on the diene (which are point at the anhydride) and the anhydride group. In the endo T.S. the C-C bond opposite the C=O-CO-C=O are sp² hybridised (and hence smaller). Hence the H atoms on the C-C opposite the anhydride are not clashing since the H atoms are parallel to anhydride group. This is supported by the green arrows which indicate the distance ebtween the atoms. It can be seen in the exo form the H and C atoms are ~0.5Å closer. A value significant enough to suggest greater steric slashes.

For greater consideration of the Diels-Alder reaction profile the IRC of the both the endo and exo T.S. were run in the forward and reverse direction separately at 100 points followed by an optimisation and frequency calculation (for thermochemistry). This was all done at the B3LYP/6-31G* level.

Temperature			0K	298K
E=Eelec+Evib+Erot+Etrans	Endo	Reactant	-384369.5762	-384361.6577
		Product	-384392.8010	-384386.8999
		T.S.	-384350.6066	-384344.1094
		ΔEACT	18.96959707	17.54828919
		ΔEREACT	23.2247356	25.24217703
	Exo	Reactant	-384361.6859	-384369.6051
		Product	-384394.4871	-384388.5471
		T.S.	-384348.015	-384341.5197
		ΔEACT	13.67091107	28.08542031
		ΔEREACT	32.80115045	18.94198667

Prior to consideration of the reaction it should be noted that the point of reference for the reactants is different for the exo and endo reactions. This is similar to the argument made in the Cope re-arrangement section - some orientations are more favourable than others and there is a barrier of interconversion between the two. Hence it is not feasible at 298.15K to go from the same lower energy reactant as the exo reactants for the endo reaction.

The energies at 298.15K shows that the reaction proceeds as expected by theory. The endo T.S. is lower in energy by ~11kcal/mol than the exo T.S. and the exo product is more stable than the endo by 1.65kcal/mol. The thermal energy available is only 0.59kcal/mol. Hence it can be seen that the difference in energy between the activation energy of the two complexes is considerable and not reversible at room temperature. Hence the reaction proceeds via kinetic control whereby the product formed is the one which has the lowest activation energy and not the lowest energy product.

Whilst reaction energies are stated at 0K no reaction is feasible since at 0K there is no thermal energy available. However approaching very very low temperatures, it can be seen that the not only does the exo product have lower reaction energy change but also a lower activation energy. This could be due to little to no nuclear motion as vibrational energy is almost 0kcal/mol. Hence steric clashes are no longer a very significant factor. The fact there is no secondary orbital overlap aiding stabalsiation of the endo transition state further reduces the difference. This may hence enable the ~5kcal/mol relative greater stability of the exo T.S. with respect to the endo transition state.

Conclusion

Transition state modelling is unique to computational chemistry. In actual experiments it is only possible to guess the transition state of molecules from theory. This can at time be very rough or even wrong (e.g. reasoning for Diels-Alder endo/exo selectivity). Guessing the transition state from the the outcome of an experimental reaction can enable theory to then be drawn upon to support or dismiss the proposed structure. Computational time itself is not excessive and justifiable considering there is not experimental alternative. Hence it provides a critical supportive role in determining the stereochemical outcome of a reaction. Nonetheless it should be treated with caution since the calculations can at times become trapped in energy minima. Thus the conformers of the reactants and products must be thoroughly considered when determining activation energies for example.