Jump to content

Rep:Mod:clras25

From ChemWiki

Module 1: Structure and Spectroscopy

Molecular Mechanics Models

All calculations in section 1.1 are based upon MM2 calculations by ChemBio3D Ultra 11.0. In this type of calculation the optimised geometry is determined by minimisation of the enegy of the conformation. This is done by applying several force fields on parameters such as stretching, bending, stretch-bending, 1,4 van der Waals', non-1,4 van der Waals and dipole/dipole energies. No orbital interactions are taken into account and bonds must be specified by the user (e.g. the planar arragement of atoms in an aromatic ring is only maintained due to the high force field on the atoms). Furthermore all energy values are placed on a relative scale to a reference. Hence actual enthalpy values can not be determined.

Further limitations of this method are considered in section 1.1.2 Stereochemistry of Nucleophilic Addition to Pyridinium Ring (NAD+ analogue).

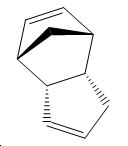
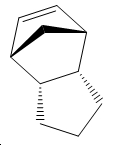
Hydrogenation of Cyclopentadiene Dimer

Molecule Exo Isomer 1 Endo Isomer 2 3 4
2D
3D
Stretch (kcal/mol) 1.2829 1.2454 1.2793 1.0963
Bend (kcal/mol) 20.5879 20.8603 19.9167 14.5074
Stretch-Bend (kcal/mol) -0.8341 -0.8320 -0.8046 -0.5493
Torsion (kcal/mol) 7.6718 9.5039 10.7500 12.4972
Non-1,4 VDW (kcal/mol) -1.4355 -1.5083 -1.2190 -1.0507
1,4 VDW (kcal/mol) 4.2324 4.3012 5.6404 4.5124
Dipole/Dipole (kcal/mol) 0.3778 0.4448 0.1621 0.1407
Total Energy (kcal/mol) 31.8832 34.0153 35.6886 31.1540


Exo Isomer 1 vs Endo Isomer 2 – Kinetic Control

The exo isomer is 2.1321 kcal/mol lower in energy than the endo isomer and hence thermodynamically the favoured product is the exo form. However this is not the case in real life and the actual isomer that predominates is the endo isomer. This inherently implies that kinetic factors are of a greater significance.

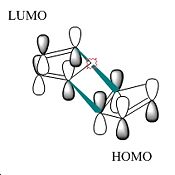
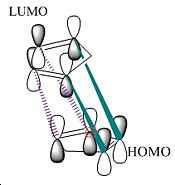
Based on simple steric observations it would appear that the endo isomer has greater strain and hence is also less favoured in terms of formation. This is supported by the torsion values (the greater the value the greater the deviation of the molecule from the staggered conformation) for the endo isomer being 1.8321kcal/mol higher. However if the orbital interactions of the two reactants in forming the endo and exo isomer is considered–

Orbital Interactions
Exo Isomer 1 Endo Isomer 2

It can be seen that there are more favourable interactions in the formation of the endo isomer (i.e. secondary orbital interactions[1] are also present due to the orientation of attack). This suggests the ΔG‡ for the endo isomer is of lower energy than the exo isomer. In kinetically controlled reactions there is usually insufficient energy to overcome both ΔG‡ barriers for both reactions. Hence the reaction is irreversible and the product with the lower ΔG‡ is the one formed. In this example it is the endo isomer. This is in accordance with real observations of the reaction.

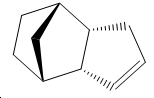
Molecule 3 vs Molecule 4 – Thermodynamic control

By comparing the energies of the two possible products with the starting endo isomer it can clearly be seen that molecule 3 is of higher energy than the starting material and hence is unlikely to form thermodynamically. Thus the isomer formed is molecule 4.

The reason for molecule 3 being of higher energy than molecule 2 is due to the removal of the C=C resulting in the introduction of greater destabalising 1,4 van der Waals forces (1.3028kcal/mol) in addition to the greater torsion (1.2461kcal/mol). This is not of set by the greater flexibility in the 5 membered ring system of the molecule as shown in the reduced bending energy (0.9436kcal/mol).

On the other hand, molecule 4 experiences a far greater reduction in bend energy (6.3529kcal/mol) despite the increased torsion (2.9933kcal/mol). This is due to the fact the C=C removed introduces greater flexibility into not one but two ring systems.

Thus molecule 4 has a far greater flexibility (reflected in the relative bends difference = 5.4093kcal/mol) for only a slightly increased torsional strain (1.7472kcal/mol) and less 1,4 van der Waals interactions (1.1280kcal/mol) with respect to molecule 3. This means that thermodynamically molecule 4 is the main product.

Stereochemistry of Nucleophilic Addition to Pyridinium Ring (NAD+ analogue)

Prolinol Reaction

Prolinol Reaction Mechanism[2] Prolinol
Pentahelicene
Total Energy = 26.3412kcal/mol
N.B. - Counter ion for reactant assumed to be Cl-

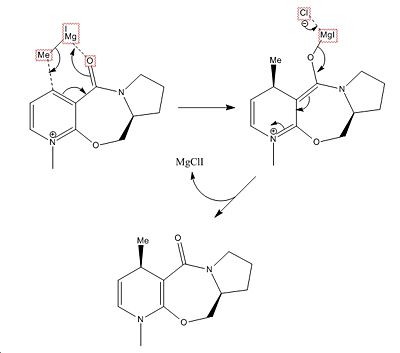
From the MM2 optimisation, the carbonyl group is 23.9547° higher than the horizontal plane thorough aromatic ring. This would seem to imply steric hindrance by the carbonyl group of attack on the same face of the ring. However for the reaction of prolinol this is not the case due to the chelation control in the reaction mechanism.

In-order for MeMgI to deliver the Me group to the ring it must first be activated by chelation of the Mg to the C=O oxygen atom. This hence results in the Me group attacking on the same face of the aromatic ring as the C=O in a cyclic transition state.

Pyridinium Ring Reaction

Pyridinium Ring Reaction Mechanism Pyridinium Ring
Pentahelicene
Total Energy = 16.2754kcal/mol
N.B. - Counter ion for reactant assumed to be Cl-

In this reaction there is no chelation control and the NPhH2 attacks on the least sterically hindered site on the aromatic ring which in this case is the opposite side to the C=O[3]. This is supported by the MM2 calculation which places the C=O group 41.9627° below the plane of the aromatic ring whilst the NPhH group is above the horizontal plane thorough the aromatic ring.

Limitations

The rings are considered aromatic but are no longer planar and hence can not gain sufficient orbital overlap for aromaticity.

One of the main limitations of MM2 calculations are their reliance on existing data. For instance the MeMgI molecule cannot be optimised due the lack of data on the Mg atom (error message - "WARNING! No atom type was assigned to selected atom!" is obtained). Hence all calculations must be done with the framework of existing knowledge and does not allow for exploration of more novel molecules.

A further limitation of MM2 is the fact orbital interactions are not taken into account. Hence this prevents the evaluation of transition states (existing data on transition states are also not well known - see above paragraph) as well as stereoelectronic effects. Furthermore reactions are normally multimolecular and involve several interactions. However the MM2 force field is unable to calculate the properties of more than one molecule. This is evident when both pyridinium ring and NPhH2 are placed into the same MM2 force field calculation (see left). This also the case for solvents and their effect on the properties of the reactants or products.


Stereochemistry and Reactivity of Taxol Synthesis Intermediate

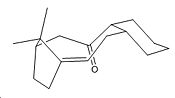
Atropisomer 1 Carbonyl Down Atropisomer 2 Carbonyl Up
Total Energy: 44.9664 kcal/mol Total Energy: 48.8805 kcal/mol

Atropisomer Stability

Bredt’s rule states that alkene bonds on bridgehead C atoms are unfavourable. This is due to the loss of sp2 character from the alkene. The bond angles at the sp2 centres are no longer 120° and the dihedral angle in the alkene are not 0° or 180°. This results in poorer p orbital interactions between the two C atoms in the alkene and hence the π bond is weaker. However in the case of the above atropisomerisms the deviation from 0° is not that great (9.0307° for the down isomer and 10.7664° the up isomer). Hence the molecules exist.[4]

Carbonyl Dihedral Angles
Atropisomer 1 Carbonyl Down Atropisomer 2 Carbonyl Up

However the more important dihedral angle is that of the carbonyl with respect to the rest of the ring. It can be seen the up isomer has a greater deviation from being in a eclipsed conformation with respect to the atoms on the adjacent carbon atoms. The main most significant interaction is that of the carbonyl and the atoms on the C in the larger membered ring. For the up isomer this angle is 30° less than for the down isomer. Hence the down isomer is more staggered and hence experiences less destablaising interactions making it more stable than the up isomer.

Alkene Reactivity

Transannular Distance
Atropisomer 1 Carbonyl Down Atropisomer 2 Carbonyl Up

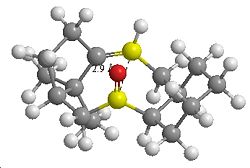
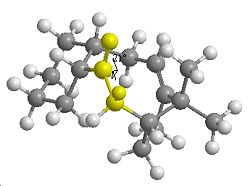
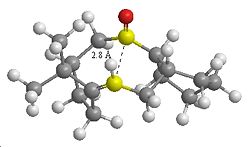
In terms of reactivity both alkenes are reported to have unusually long reaction times. This could be due to the fact that one face of attack on the alkene is not available due the ring structure. In terms of kinetics factors, the hydrogenated product should be considered. The sp3 re-hybridisation of C atoms may result in additional transannular H H atom repulsion on the inside of the the ring.

There could also be transannular interactions between the π molecular orbital of the alkene and the π* of the carbonyl group. Due to the structure of the ring system in the lowest energy conformation of the molecules the interactomic distance between the two groups is ~2.8Å (up isomer) or ~2.9Å (down isomer). This is a typical distance for transannular interactionsdoi [5] and furthermore the orbitals appear to be orientated at the appropriate angle for the interaction to occur. Hence less electron density is available at the C=C for electrophilic attack.

Therefore the lower reactivity could be attributed to stereoelectronic (πC=C→π*C=O) and steric factors (only one face of the alkene available for attack and transannular H H repulsion).

Room Temperature Induced Hydrolysis of Peptide

Kinetic Behaviour

In both the trans and cis decalin systems it can be seen that when the amide group is in an equatorial position the energy of the molecule is lower. This is due to 1,3 diaxial compressions occurring when in an axial position causing the molecule to experience greater steric strain.

It takes far less time for the cis decalin isomers of the molecule to undergo hydrolysis of the amide bond in comparison to the trans decalin isomers. This is mainly due to the orientation of the OH group with respect to the amide bond.

Trans Decalin Isomers (OH group axial and t1/2=840)
Axial R on N Equatorial R on N
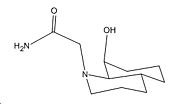
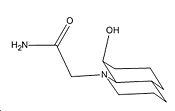
Total Energy: 12.0143 kcal/mol Total Energy: 9.1720 kcal/mol

In the trans isomers, the hydrogen bonding is present that orientates the OH group in such a way that it cannot attack the amide bond easily. Both lone pairs on the OH group point away from the amide bond and are not orientated according to the Bürgi-Dunitz[6] angle of attack on C=O (π*) - 107° above or below the plane of the C=O. Furthermore for the reaction to be successful the amide group on the N atom has to be aligned in the same direction as the OH group (which in this case is axial)[7]. Otherwise the transition state cannot be achieved without larger steric strain than the energy required to interconvert between isomers. The axial amide isomer of the trans decalin system is of a higher energy than the equatorial position by 2.8423kcal/mol. Thus for the hydrolysis to occur the more unfavourable of the two isomers must reached i.e. only a smaller proportion of the molecules available are able to reach the transition state. Thus poor orbital interactions (kinetics) and the need to go up a thermodynamic hill mean the t1/2 is far longer at 840mins.

Cis Decalin Isomers (OH group equitorial and t1/2=21)
Axial R on N Equatorial R on N
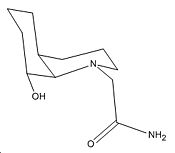
Total Energy: 19.2736 kcal/mol Total Energy: 13.3786 kcal/mol

In the cis system the lone pair of OH group is directly in line with the C=O π* orbital position (although it does not approach from the Bürgi-Dunitz angle) when the amide group is equatorial (the same as the OH group). Furthermore this isomer is lower in energy than the other isomer where the amide group is axial (by 5.895kcal/mol). Hence thermodynamically the equatorial isomer is far more abundant in the equilibrium between the isomers. Thus kinetically and thermodynamically the reaction occurs far more readily.

Peptide Hydrolysis

Peptides exist in the form of proteins and enzymes and are far more difficult to hydrolyse than the above isomers. This is due to the intramolecular nature of attack in the decalin isomers. Intramolecular attack effectively reduces the reaction kinetics, order of reaction from two to one. Hence instead of the orientation and distance of two molecules, only the orientation of one group in a molecule is important. Thus in terms of probability, intramolecular hydrolysis is far easier to achieve.

It should be noted that whilst it takes 500 years for hydrolysis of a acetylglycine-glycine peptide bond[8], t1/2 of amino acids which possess an OH group in their R side chains may be far lower. These R groups would enable first order reaction kinetics and may facilitate t1/2 of less than a year.

Peptide Kinetics Terminal Amide Kinetics
v=k[H2O][Peptide] v=k[Decalin Isomer]
Second Order First Order

Semi-empirical and Density Functional Theory (DFT) Molecular Orbital Models

In this section (1.2) two models were used to improve upon the MM2 optimisations. The first model is semi-empirical and involves only solving simpler integrals in quantum mechanical calculations (PM3). Orbital interactions and electronic properties are also taken into account. There are however inaccuracies due to more complex integrations being approximated using experimental values. Hence in-order to calculate spectroscopic data, some of these integrals have to be solved. This is done using a DFT model. This model cannot be used as the first and only optimisation as it may not be able to determine the correct geometry (i.e. cruder optimisations are required first). The DFT B3LYP/6-31G was used for optimisation of geometries, DFT B3LYP/6-31G(d,p) for IR data, DFT MPW1PW91/6-31G(d,p) for NMR and DFT B3LYP/aug-cc-pvdz for optical rotation. DFT models involve more calculations than any of the previous methods and hence are also the most time consuming.

Regioselective Addition of Dichlorocarbene

Electrophilic Attack

The alkene bond in the exo position is the preferred site of attack for electrophiles in comparison to the endo C=C. Based solely on steric factors, this is not the expected result. The steric bulk of the Cl should in theory hinder electrophilic attack on one face of the exo alkene whereas the endo alkene experiences no such difficulty from elecrophilic attack. However as seen previously orbital interactions are of key importance.

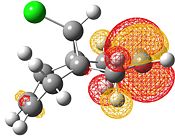
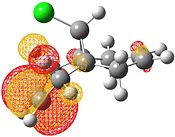
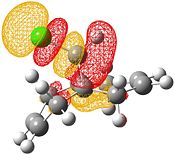
HOMO-1 HOMO LUMO LUMO+1 LUMO+2

Electrophilic attack on the alkenes is clearly dependent on the distribution of electron density in the HOMO. If the HOMO is considered, it can be seen that there is more electron density at the exo bond and hence attack at that position is favoured.

The reason for the exo π orbital being of a higher energy than the endo π orbital is due to the interactions of the πC=C (endo)→σ*C=O[9]. This can be visualised from the interaction of the HOMO-1 with the LUMO+2. This transfer of electron density results in the endo π orbital being lowered in energy. However no such interaction happens for the exo C=C. This can be visualised by comparison of the HOMO to the LUMO, LUMO+1 and LUMO+2 - all of which do not possess vacant antibonding orbitals of appropriate symmetry and orientation to accept electron density from the exo π bond.

I.R. Spectra Comparison

Dialkene 12 (PM3 opt 3D) Monohydrogenated Molecule (PM3 opt 3D)
Pentahelicene
Pentahelicene


I.R. Vibrations
C-Cl Stretch (cm-1) C=C Stretch (cm-1) I.R. Spectrum
Dialkene 12[10] 772.633 1740.77 and 1760.95
Monohydrogenated Molecule[11] 777.223 1761.76

The I.R. data does correspond to the observations made on the site of electrophilic attack. In the dialkene there are two C=C stretches with a large difference of 20.18cm-1. This is due the strength of the endo C=C being weaker than the exo C=C. πC=C (endo)→σ*C=O interactions mean that the endo C=C has more single bond character than the exo C=C.

The wavenumbers can be converted to energy by the equation E=hc/λ where h is Planck's constant, c is the speed of light and λ is the wavelength. 1/λ is equivalent to wavenumber. From the equation it can be seen that the smaller, the wavenumber the smaller the energy. Furthermore the wavenumber is related to to force constant of a bond by the equation wavenumber=v/c=1/2πc√k/m (v is frequency and m is the mass). The equation shows wavenumber is proportional to k (force constant). Hence the higher the wavenumber the stronger the bond.

Thus the 1740.77cm-1 must correspond to the lower energy π endo orbital. This is further supported by looking at the C=C stretch in the hydrogenated product. In the product, the endo C=C was hydrogenated leaving only the higher energy exo C=C. Hence the wavenumber that is no longer present (1740.77cm-1) must correspond to the endo C=C. The increase in the wavenumber of the C-Cl stretch also indicates that the πC=C (endo)→σ*C=O no longer exists. Since this interaction has been removed, the C-Cl bond is higher in energy (i.e. stronger) as no electron density is being placed in the σ*.

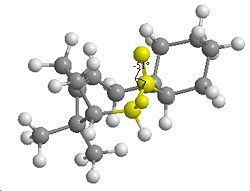
Photochemical [2+2] Cycloaddition Addition Reaction [12] Project

Reaction Mechanism[12]

The reaction is bi-radical reaction that is induced by hv. The ratio of products A and B is dependent on temperature but at the conditions stated in the journal (Acetone/Quartz, 8 h/25 °C), product A was the major product.

Mechanistic determination of the product in photochemical reactions are infamously difficult to analyse but the large difference in MM2 energies between the two products and the reversible nature of reaction enables thermodynamic predictions. Product A (43.9848 kcal/mol) is energetically more stable than product B (48.0247kcal/mol) by 4.0399 kcal/mol.

Product A experiences no steric interactions (two 1,2 and one 1,3 interactions) between the Ph group and the two five membered rings which face in the opposite direction. Although it does encounter destablising 1,3 interaction between the Ph and Me groups. Nonetheless this is a more favourable situation than the interactions in product B. Hence thermodynamically product A is more stable. The reversibility of the entire reaction process means thermodynamic control prevails. Thus the equilibrium in the mixture between the two products should be in the favour of product A.

Isomer Determination

Product A (DFT opt 3D) Product B (DFT opt 3D)
Pentahelicene
Pentahelicene
Total Energy (MM2) = 43.9848 kcal/mol Total Energy (MM2) = 48.0247 kcal/mol

There are various spectroscopic techniques that can be used to determine isomers, however, the most useful in (computationally) is 13C NMR. Mass spectroscopy, whilst useful in identifying the molecular formula via the molecular ion, is not in identifying isomers. The isomer fragmentation pathway may be different for each isomer but it is hard to interpret. Melting points are also potential identifiers due to the different orientation of groups resulting in different intermolecular interactions which may raise or lower the melting point. However computational modelling may be difficult. UV-vis spectroscopy is of least use since the chromophores, in the form of functional groups, are not altered and hence only in very rare occasions is this technique used. If the product can be crystallised (which are sufficiently big and diffract) as required by X-ray crystallography, this technique is most useful in identification. However a large proportion of products are not crystalline, diffract, are liquids etc. Hence this technique is of limited use.

However three main types of spectroscopy are very adept at isomer identification - NMR, IR and optical rotation. These techniques are detailed below with respect to the [2+2] cycloaddition reaction.

13C NMR (CDCl3)

Product A Lit.[12] (δ ppm) 176.6 141.5, 128.9 127.2 126.4 112.7 76.0 50.6 47.4 47.1 45.2 18.4
Product A Calc.[13] (δ ppm) 177.77* 138.62 123.36 (several peaks) 110.34 74.26 51.93 49.33 45.61 44.87 19.57
Product B Lit.[12] (δ ppm) 175.3 136.0 128.4 127.6 126.9 111.4 69.9 52.0 45.6 44.5 36.7 18.3
Product B Calc.[14] (δ ppm) 176.27* 134.98 124.71 (several peaks) 122.55 109.22 68.52 53.03 46.18 44.74 38.62 19.16 
* Values corrected to take into account C is part of ester (correction is δcorr = 0.96δcalc + 12.2

The lit. and calculated NMRs match up very well (the largest difference in ppm being ~3). The reason for multiple peaks being visible in the calc. NMR despite only one or two peaks being present in the lit. NMR may be due to degeneracy. The lit. does not state the degeneracy of any signals, however, the calc. does state degeneracy. Furthermore all the extra peaks in the calc. NMR are Ph C atoms. Hence the aromatic system may not be modelled sufficiently to exhibit actual NMR data i.e. correction factors may be required. Thus the aromatic C atoms may in fact be degenerate in experimental spectra resolution but are not so in calc. NMR spectra.

The main benefit of modelling the reaction and comparing to lit. is that it enables easier identification of the C atom responsible for the peak. This can be done on real spectra as well through theoretical principles, however, the degree of certainty is less and requires high levels of understanding of quantum mechanics. Thus, in the identification of isomer, the atoms of concern (the one changed chemically in the isomers) can be easily identified. Hence the calc. spectra act as confirmation of the experimental NMR data.

In the case of this reaction the signal of interest is the C atom where the Ph ring is either placed up or down. In product A the value for this shift is 45.61ppm; in product B the value for the shift is in fact 38.62ppm. Therefore the difference between these signals is 6.99ppm - a significant value. This collaborated by the lit. values for the two product (A - 47.1ppm;B - 36.7ppm).

This technique is most efficient due to the lower computational demand (time) for the degree of accuracy required (both NMR caclulations only took ~10mins and have a high degree of accuracy).

1H NMR

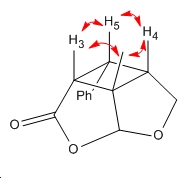
Lit. determination of the isomers was through Nuclear Overhauser Effect (nOe) 1H NMR. In this type of NMR, one H atom is irradiated and energy is equilibrated via cross relaxation to neighbouring H atoms within ~3.5Å. These H experience a signal enhancement as a result. In product A and B, the following effects would be seen -

Product A Product B
Product A only causes signal enhancement of the Me axial H whereas

product B causes signal enhancement of the Me H and H5 when H3 and H4 are irradiated.[12]

However computational analysis of 1H NMR is difficult as achieving chemical shift accuracy is not sufficiently high and unreliable (unless time consuming high level optimisation calculations are done). The 1H NMR lit. values are detailed in the reference[12].

I.R. Spectra

Whilst the stretches of certain bonds can be ascertained, it is not of use in the isomer determination of these products. This is because the error in IR vibrations is too great to investigate small changes in wavenumber of specific bonds. Furthermore it is of more use to interpret the stretches in the starting material and relate it to orbital interactions (as stated in the dichlorocarbene exercise). However the mechanism by which the reaction proceeds (bi radical mechanism) is very hard to analyse for orbital interactions. Lit. IR data is available in the reference[12].

Product A[15] Product B[16]

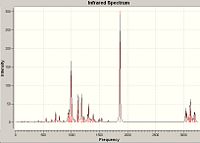
Optical Rotation

This is the method of choice in optical isomer determination if only chiral centres are present. The steriocentres of products A and B can be assigned as follows with the [α]D calculated by SCAN -

Product A Product B[17]
[α]D=-50.64° [α]D=-56.39°

Theoretical determination of these values is hard but when compared with experimental calculations of optical rotation, it would enable identification of the isomer in question (all possible optical isomers can be modelled by computational methods). Whilst this type of modelling is very good at isomer determination, it does result in high computational times (calculations times were 23hrs and 15hrs for products A and B respectively) due to the demanding nature of the calculations. It should be noted that lit. optical rotation values could not be found.

Conclusions

Computational modelling of reactions is of great aid in analysis of experimental data or theoretical predictions. Different conformations and isomers can be modelled and their properties can be compared to experimental values. Whilst calculations to achieve this level of accuracy are time consuming, they can be more rapid than some reactions which require long refluxes, crystallisation time etc. Thus computational modelling (at higher level calculations) is useful support for all areas of chemistry.

References

  1. ↑ Hoffmann, R.; Woodward, R. B., J. Am. Chem. Soc., 1965, 87, 4388 DOI:10.1021/ja00947a033
  2. ↑ A. G. Shultz, L. Flood and J. P. Springer, J. Org. Chemistry, 1986, 51, 838 DOI:10.1021/jo00356a016
  3. ↑ S. Leleu, C. Papamicael, F. Marsais, G. Dupas, V. Levacher, Tetrahedron: Asymmetry, 2004, 15, 3919-3928 DOI:10.1016/j.tetasy.2004.11.004
  4. ↑ G. Köbrich, Angewandte Chemie International Edition in English, 1973, 12, 464-473 DOI:10.1002/anie.197304641 10.1002/anie.197304641
  5. ↑ J. E. Gurst, E. M. Schubert, S. E. Boiadjiev and D. A. Lightner, Tetrahedron, 1993, 49, 9191-9196 DOI:10.1016/0040-4020(93)80006-F
  6. ↑ H. B. Bürgi, J. D. Dunitz, and Eli Shefter J. Am. Chem. Soc., 1973, 95(15), 5065 - 5067 DOI:10.1021/ja00796a058
  7. ↑ M. Fernandes, F. Fache, M. Rosen, P.-L. Nguyen, and D. E. Hansen, J. Org. Chem., 2008, 73, 6413–6416 DOI:10.1021/jo800706y
  8. ↑ A. Radzicka and R. Wolfenden, J. Am. Chem. Soc., 1996, 118, 26, 6105 - 6109 DOI:10.1021/ja954077c
  9. ↑ B. Halton, R. Boese and H. S. Rzepa., J. Chem. Soc., Perkin Trans 2, 1992, 447 DOI:10.1039/P29920000447
  10. ↑ DOI:10042/to-1008
  11. ↑ DOI:10042/to-1009
  12. ↑ 12.0 12.1 12.2 12.3 12.4 12.5 12.6 N. Braussaud, N. Hoffmann and H.-D. Scharf, Tetrahedron, 1997, 53, 14701-14712 DOI:10.1016/S0040-4020(97)01046-6
  13. ↑ DOI:10042/to-1005
  14. ↑ DOI:10042/to-1006
  15. ↑ DOI:10042/to-1003
  16. ↑ DOI:10042/to-1004
  17. ↑ DOI:10042/to-1007
Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod:clras25&oldid=818928"