Rep:Mod:clc09mod3

Year 3 Computational Chemistry: Chew Chee Leong

Module 3

Introduction

In this module, we learn to characterise transition structures on potential energy surfaces for the Cope rearrangement and Diels Alder cycloaddition reactions. Since the focus is on the transition structures of larger molecules, there are no longer suitable formulae for the energy, and the molecular mechanics / force field methods that work well for structure determination cannot be used as they do not describe bonds being made and broken, and changes in bonding type / electron distribution. Therefore, the new solution involves molecular orbital-based methods, numerically solving the Schrödinger equation, and locating transition structures based on the local shape of a potential energy surface. In addition to transition structures, reaction paths and barrier heights are also calculated.

Part 1: The Cope Rearrangement Tutorial

In this tutorial we will use the Cope rearrangement of 1,5-hexadiene as an example of how to study a chemical reactivity problem. The objectives are to locate the low-energy minima and transition structures on the C₆H₁₀ potential energy surface, to determine the preferred reaction mechanism.

Diagram 1: Cope Rearrangement

Optimizing the Reactants and Products

Ten possible conformers of 1,5-hexadiene were subjected to optimisation via the HF/3-21G method, followed by re-optimisation using the B3LYP/6-31G(d) method. At the same level of theory, a frequency calculation was performed. In addition to that, the corresponding energies of conformers were determined. Note that the conformers readily inter-convert at room temperature by means of C-C sigma bond rotation.

Conformer	Structure	Point Group	HF/3-21G Optimisation	B3LYP/6-31G(d) Re-optimisation	Σ (Eelec + ZPE)	Σ (Eelec + Etherm)	Σ (Helec + Htherm)	Σ (Gelec + Gtherm)
Gauche 1		C2	-231.68771604	-234.60787891	-234.465253	-234.458119	-234.457175	-234.495483
Gauche 2		C2	-231.69166700	-234.61070757	-234.468206	-234.460939	-234.459995	-234.499103
Gauche 3		C1	-231.69266120	-234.61132934	-234.468693	-234.461464	-234.460520	-234.500105
Gauche 4		C2	-231.69153030	-234.61048196	-234.467784	-234.460521	-234.459577	-234.498690
Gauche 5		C1	-231.68961572	-234.60911048	-234.466369	-234.459214	-234.458270	-234.497439
Gauche 6		C1	-231.68916017	-234.60888834	-234.466281	-234.459103	-234.458159	-234.497369
Anti 1		C2	-231.69260236	-234.61180037	-234.469286	-234.461965	-234.461021	-234.500162
Anti 2		Ci	-231.69253528	-234.61170280	-234.469212	-234.461856	-234.460912	-234.500821
Anti 3		C2h	-231.68907065	-234.60964388	-234.466992	-234.459816	-234.458872	-234.497337
Anti 4		C1	-231.69097055	-234.61078875	-234.468193	-234.460941	-234.459997	-234.499482

Note

Σ (E_elec + ZPE): denotes potential energy at 0 K including the zero-point vibrational energy.

Σ (E_elec + E_therm): denotes energy at 298.15 K and 1 atm of pressure, including contributions from translational, rotational & vibrational energy modes

Σ (H_elec + H_therm): denotes additional correction for RT (H = E + RT).

Σ (G_elec + G_therm): denotes entropic contributions to the free energy (G = H - TS)

Conformer	DOI [HF/3-21G]	DOI [B3LYP/6-31G(d)]	DOI [Freq]
Gauche 1	DOI:10042/to-12368	DOI:10042/to-12373	DOI:10042/to-12379
Gauche 2	DOI:10042/to-12361	DOI:10042/to-12374	DOI:10042/to-12380
Gauche 3	DOI:10042/to-12360	DOI:10042/to-12375	DOI:10042/to-12381
Gauche 4	DOI:10042/to-12362	DOI:10042/to-12376	DOI:10042/to-12382
Gauche 5	DOI:10042/to-12363	DOI:10042/to-12377	DOI:10042/to-12383
Gauche 6	DOI:10042/to-12364	DOI:10042/to-12378	DOI:10042/to-12384
Anti 1	DOI:10042/to-12365	DOI:10042/to-12369	DOI:10042/to-12385
Anti 2	DOI:10042/to-12359	DOI:10042/to-12370	DOI:10042/to-12386
Anti 3	DOI:10042/to-12366	DOI:10042/to-12371	DOI:10042/to-12387
Anti 4	DOI:10042/to-12367	DOI:10042/to-12372	DOI:10042/to-12388

In terms of energy, the HF/3-21G method predicted Gauche 3 to be the most stable conformer whereas the B3LYP/6-31G(d) method suggested otherwise; Anti 1 is found to be most stable. Since the B3LYP/6-31G(d) method is more sophisticated than the 'primitive' HF/3-21G, Anti 1 is overall the most stable conformer at room temperature.

Optimizing the "Chair" and "Boat" Transition Structures

In this section, the "chair" and "boat" transition structures for the Cope rearrangement were optimised by computing the force constants at the beginning of the calculation, (2) using the redundant coordinate editor, and also (3) QST2. In addition, we attempt to visualize the reaction coordinate, run the IRC (Intrinsic Reaction Coordinate) and compute the activation energies for the Cope rearrangement via the "chair" and "boat" transition structures.

Chair TS: Optimization to a TS (Berny)

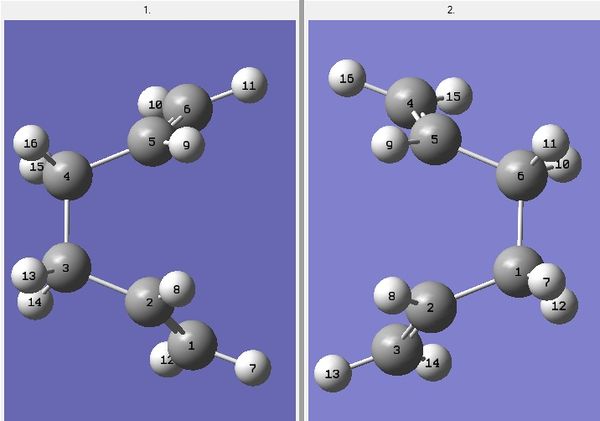
The allyl fragments of the guess structure were positioned 2.20075Å apart. The optimisation process was successful; an imaginary vibrational frequency at -818.02cm^-1 was found and its vibrational mode can be observed HEREDOI:10042/to-12389 . After optimisation, the distance between the terminals has decreased to 2.02029Å and the fragments appeared slightly bent.

Chair TS: Optimization via Frozen coordinate method

This method was unique in the sense that the terminal ends were "frozen" at a distance of 2.20075Å using the Redundant Coord Editor and optimised. When the job is done, the fragments were "unfrozen" and optimised again. The separation between the two terminal ends was 2.19999Å for the frozen structure and 2.02037Å for the unfrozen structure. The final conformations were nearly identical, suggesting both methods were in good agreement with each other. ( DOI:10042/to-12390 ; DOI:10042/to-12391 )

Boat TS : QST2 Method

Using an optimised Anti 2 conformer, a pair of Reactant and Product conformers were modelled. All the atomic labels have been changed. For the boat transition state to be located, the central C-C-C-C dihedral angle was changed to 0^o, while the central C-C-C were reduced to 100^o.

Diagram 2: 1 = Reactant, 2 = Product

After arranging the atoms in a specific way, the structures were optimised using the method below:

opt=qst2 freq hf/3-21g geom=connectivity

Another imaginary vibrational frequency at -839.98cm^-1 was found and its vibrational mode is animated HEREDOI:10042/to-12402 . The distance between the two terminal ends was 2.15000Å, which is slightly longer than the chair transition state.

Intrinsic Reaction Coordinate (IRC) Analysis

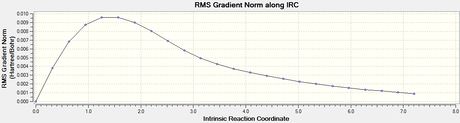
To verify whether the above transition states were fully optimised, the IRC method is helpful where it uses the imaginary vibrational mode found in the frequency analysis above to determine energetic stability in steps. This gives a good indication on whether the transition state is at the maximum of an energy diagram.

Optimized chair transition structure

DOI:10042/to-12411

Final Conformation of Chair TS	Total Energy	RMS Gradient

Optimized boat transition structure

DOI:10042/to-12413

Final Conformation of Boat TS	Total Energy	RMS Gradient

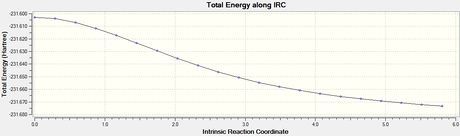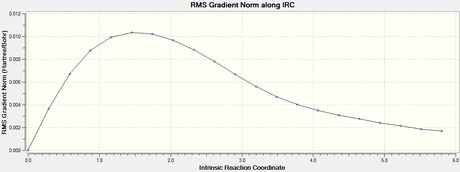Activation energies

The activation energies were solved by taking the difference in energy, ΔE, between the energies of the transition state (the maximum) and the energies of anti 2 (the minimum). Σ (E_elec + ZPE) gave the energy difference, i.e. the activation energy, at 0 K and Σ (E_elec + E_therm) gave the energy difference at 298.15 K.

	HF/3-21G: ChairDOI:10042/to-12418 and BoatDOI:10042/to-12417 TS			DFT B3LYP/6-31G(d): ChairDOI:10042/to-12415 and BoatDOI:10042/to-12416 TS
Transition State	Electronic Energy	Σ (Eelec + ZPE)	Σ (Eelec + Etherm)	Electronic Energy	Σ (Eelec + ZPE)	Σ (Eelec + Etherm)
Chair TS	-231.61952	-231.46570	-231.46234	-234.55697	-234.41483	-234.39901
Boat TS	-231.60280	-231.45093	-231.44530	-234.56309	-234.40241	-234.39601
Anti 2 conformer	-231.69254	-231.53954	-231.53257	-234.61174	-234.46931	-234.46086

Activation Energies /kcalmol^-1

	HF/3-21G		DFT B3LYP/6-31G(d)
	@ 0 K	@ 298.15 K	@ 0 K	@ 298.15 K
ΔE Chair	46.68	44.66	34.56	33.49
ΔE Boat	57.09	54.88	42.74	41.97

Part 2: The Diels Alder Cycloaddition

Optimisation of cis-butadiene and molecular orbitals

Using Gaussview, a cis-butadiene molecule was drawn and then optimised using the AM1 Semi-empirical method. Its molecular orbitals in the HOMO-LUMO region and symmetry were also elucidated.

Molecular Orbital	Front View	Bird's eye View	Symmetry in Horizontal Plane	Symmetry in Vertical Plane
LUMO		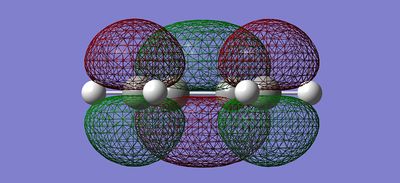	Antisymmetric	Symmetric
HOMO			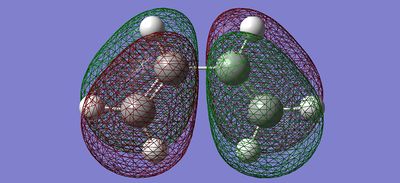Antisymmetric	Antisymmetric

Optimisation of transition state of cis-butadiene and ethene

In order to construct a transition state model between the reaction of cis-butadiene and ethene, we have to build a starting geometry. This is done by building a bicyclo system (b) and then remove the -CH₂-CH₂- fragment. The inter-fragment distance (dashed lines) was initially guessed to be 2.50000Å prior to optimisation. The starting geometry was then optimised via the following command: # opt=(calc,ts) freq rb31yp/6-31g(d) geom=connectivity

Diagram 3: Constructing the starting geometry

Result

HOMO and LUMO Sketch

Molecular Orbital	Front View	Side View	Symmetry in Horizontal Plane	Symmetry in Vertical Plane
LUMO			Antisymmetric	Symmetric
HOMO			Antisymmetric	Antisymmetric

The HOMO of the Transition State is a combination of the HOMO of cis-butadiene and the LUMO of ethene whereas the LUMO of the Transition State consists of the LUMO of cis-butadiene and the HOMO of ethene. This finding is consistent with the symmetries observed; the HOMO of TS is antisymmetric since it is made from two antisymmetric MO's, while the LUMO of TS is symmetric due to two symmetric MO's.

Geometry of the transition structure

Optimised Transition State

After optimisation DOI:10042/to-12546 , the bond-lengths of the partly formed σ C-C bonds were found to be 2.27251Å. The typical sp³ and sp² C-C bond lengths are 1.50Å . while the Van der Waals radius of a carbon atom is 1.70Å. The partly formed σ C-C bond in the TS is longer than the typical sp³ and sp² C-C bond by 0.77251Å, suggesting the bond formation is still on its way to completion.

Frequency analysis

An imaginary frequency was found at -524.81cm^-1, which corresponded to the reaction path at the transition state. Reaction proceeded in a Syn fashion. Click HERE to view the vibrational mode. The lowest positive frequency (135.84cm^-1) displayed wagging, which had little to do with the reaction pathway. However, the vibrational mode at 284.48cm^-1 bore some resemblance to the reaction pathway.

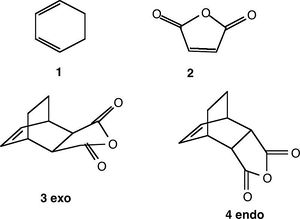
The regioselectivity of the Diels Alder Reaction

The cycloaddition reaction between cyclohexa-1,3-diene and maleic anhydride produces two isomers; endo and exo. The major product is the endo adduct. Assuming the reaction is under kinetic control, the exo transition state will therefore be higher in energy.

Optimisation of transition states

The transition states were optimised via the semi-empirical AM1 method:

Molecular Orbitals

Conformation	HOMO	LUMO
Endo
Exo

Vibrational analysis

Conformation	Imaginary Frequency (cm-1)	Vibrational Mode	DOI
Endo	-19.92	Animate	DOI:10042/to-12547
Exo	-29.52	Animate	DOI:10042/to-12548

Intrincsic Reaction Coordinate analysis

The IRC method (forward) was performed to verify the complete optimisation of the transition states.

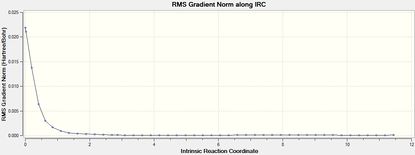
Isomer	Total Energy	RMS Gradient	Final Conformation
Endo DOI:10042/to-12555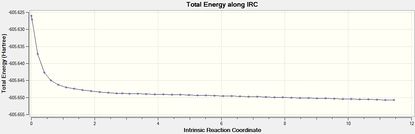
Exo DOI:10042/to-12554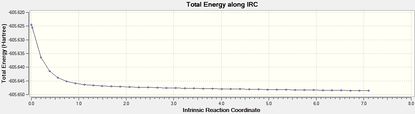

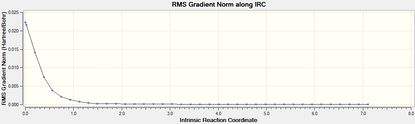The transition states were well optimised, given the RMS gradient graphs of both endo and exo isomer displayed an asymptote.

Relative Energies of the transition states

The relative energies of the transition states were as follows:

Isomer	Relative Energy (AM1)/Eh	Final Isomer	Relative Energy (AM1)/Eh
Endo	-0.051867	IRC Forward: Step 46	-0.160631
Exo	-0.050577	IRC Forward: Step 39	-0.156809

The endo transition state was lower in energy than the exo transition state; meaning it is the thermodynamically more stable product.