Rep:Mod:clc09mod2
Year 3 Computational Chemistry: Chew Chee Leong
Module 2: Computational (Inorganic) Chemistry
Introduction
In this module, we explore various quantum mechanical and computational methods which allow us to (1) optimise the energies of molecules, (2) solve the Schrödinger's equation (electronic structures) and thus obtain molecular orbitals (MO), and (3) perform vibrational analysis and obtain IR spectra. Depending on the molecule being investigated, larger and more complex models will need more computational power (SCAN) and time. Nevertheless, the density functional theory (DFT) approach via B3LYP method will get most of the work done since it can estimate molecular structures to a high degree of accuracy at the cost of very little computational processing.
Part 1: Analysis of BH3
Optimisation of BH3
Below is the summary file of BH3 optimisation on Gaussian using the DFT/ B3LYP method:
BH<sub>3</sub> optimisation File Name = BH3_OPTIMISATION File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = 3-21G Charge = 0 Spin = Singlet E(RB3LYP) = -26.46226433 a.u. RMS Gradient Norm = 0.00004507 a.u. Imaginary Freq = Dipole Moment = 0.0000 Debye Point Group = D3H Job cpu time: 0 days 0 hours 0 minutes 9.0 seconds.
The value of RMS gradient = 0.00004507 a.u. (<0.001), meaning the optimisation was complete; the optimised form should be on the stationary point of the energy graph (i.e. located at the minimum of the 1st derivative). Convergence of the job was also examined:
Item Value Threshold Converged?
Maximum Force 0.000090 0.000450 YES
RMS Force 0.000059 0.000300 YES
Maximum Displacement 0.000352 0.001800 YES
RMS Displacement 0.000230 0.001200 YES
Predicted change in Energy=-4.580970D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1945 -DE/DX = -0.0001 !
! R2 R(1,3) 1.1945 -DE/DX = -0.0001 !
! R3 R(1,4) 1.1945 -DE/DX = -0.0001 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
From the data on Gaussview, the (B-H) bond lengths were 1.19453Å (Literature value = 1.19Å)[1], while the (H-B-H) bond angles were 120o , suggesting the molecule was trigonal planar.
Diagram 1: Optimisation output
Molecular orbital analysis of BH3
The following MO were constructed using Gaussview and their corresponding energy levels were recorded:
| Orbital Geometry | Energy /eV | Molecular Orbital Structure |
|---|---|---|
| 2e' (degenerate) | 0.17928 |  
|
| 3a1' | 0.16589 | 
|
| 1a2 (LUMO) | -0.06821 | 
|
| 1e' (HOMO) (degenerate) | -0.35290 |  
|
| 2a1' | -0.51516 | 
|
| 1a1' | -6.76641 | 
|
Gaussian predicted two pairs of degenerate orbitals 1e' and 2e' accurately; as shown in conventional BH3 MO diagrams. Gaussian also predicted 2e' to be higher in energy than 3a1'. However, the ordering of these orbitals in terms of energy may be hard to rationalise.
NBO analysis of BH3
The charge distribution of BH3 was calculated using DFT/B3LYP method. The Boron atom is green and has a charge of +0.33161, while the hydrogen atoms are dark-red and have a charge of -0.11054. The net charge here is 0; or apolar since the molecule is symmetrical.
Diagram 2: NBO & charge distribution of BH3
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
B 1 0.33121 1.99904 2.66976 0.00000 4.66879
H 2 -0.11040 0.00000 1.11008 0.00032 1.11040
H 3 -0.11040 0.00000 1.11008 0.00032 1.11040
H 4 -0.11040 0.00000 1.11008 0.00032 1.11040
=======================================================================
* Total * 0.00000 1.99904 6.00000 0.00097 8.00000
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.99851) BD ( 1) B 1 - H 2
( 44.49%) 0.6670* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.0000 0.0000
0.8165 0.0000 0.0000 0.0000
( 55.51%) 0.7451* H 2 s(100.00%)
1.0000 0.0000
2. (1.99851) BD ( 1) B 1 - H 3
( 44.49%) 0.6670* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 55.51%) 0.7451* H 3 s(100.00%)
1.0000 0.0000
3. (1.99851) BD ( 1) B 1 - H 4
( 44.49%) 0.6670* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 -0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 55.51%) 0.7451* H 4 s(100.00%)
1.0000 0.0000
4. (1.99904) CR ( 1) B 1 s(100.00%)
1.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000
5. (0.00000) LP*( 1) B 1 s(100.00%)
The data above showed that Boron atom was sp2 hybridised.
Vibrational analysis of BH3
| Vibrational mode | Frequency/cm-1 | Intensity | Point Group | Animation |
|---|---|---|---|---|
| 1 | 1146.03 | 92.6653 | a2" | |
| 2 | 1204.86 | 12.3919 | e' | |
| 3 | 1204.86 | 12.3944 | e' | |
| 4 | 2591.65 | 0.0000 | a1' | |
| 5 | 2730.07 | 103.8565 | e' | |
| 6 | 2730.07 | 103.8497 | e' |
There were six vibrational modes. The frequencies show positive values; indicating complete optimisation of the molecule whereas negative values would mean that the molecule could be in the transition state and not in the ground state.
Diagram 3: IR spectrum of BH3
Part 2: Analysis of TlBr3
Optimisation of TlBr3
Optimisation of TlBr3 via the DFT/B3LYP method was done under the condition of restricting its symmetry the point group to D3h and setting the tolerance from default to very tight. This is a special case and reason behind is to avoid problems with vibrational analysis in the later part. A pseudo potential or LanL2DZ was chosen for the basis set because TlBr3 is heavy and contains many electrons. Also, Tl and Br atoms may exhibit relativistic effects that cannot be recovered by the standard Schrödinger wave equation. From the optimised version, the Tl-Br bond distance = 2.65095Å (Literature = 2.65Å)[2] while the Br-Tl-Br bond angle = 120.000o
Below is the summary file of TlBr3 optimisation on Gaussian using the DFT/ B3LYP method:
TlBr3 optimisation File Name = TLBR3_OPTIMISATION File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2DZ Charge = 0 Spin = Singlet E(RB3LYP) = -91.21812851 a.u. RMS Gradient Norm = 0.00000090 a.u. Imaginary Freq = Dipole Moment = 0.0000 Debye Point Group = D3H Job cpu time: 0 days 0 hours 0 minutes 29.0 seconds.
RMS Gradient = 0.00000090 (<0.01); optimisation is complete
Item Value Threshold Converged?
Maximum Force 0.000002 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000022 0.001800 YES
RMS Displacement 0.000014 0.001200 YES
Predicted change in Energy=-6.082801D-11
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 2.651 -DE/DX = 0.0 !
! R2 R(1,3) 2.651 -DE/DX = 0.0 !
! R3 R(1,4) 2.651 -DE/DX = 0.0 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Convergence of parameters; optimisation is complete
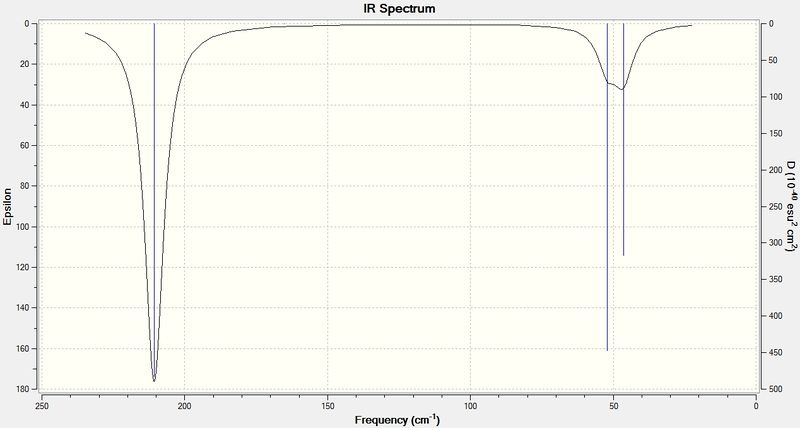
Vibrational analysis of TlBr3
Below is the summary file of TlBr3 frequency on Gaussian using the DFT/ B3LYP method:
TlBr3 frequency File Name = CLC09_TLBR3_FREQ File Type = .log Calculation Type = FREQ Calculation Method = RB3LYP Basis Set = LANL2DZ Charge = 0 Spin = Singlet E(RB3LYP) = -91.21812851 a.u. RMS Gradient Norm = 0.00000088 a.u. Imaginary Freq = 0 Dipole Moment = 0.0000 Debye Point Group = D3H Job cpu time: 0 days 0 hours 0 minutes 40.0 seconds.
| Vibrational mode | Frequency/cm-1 | Intensity | Point Group | Animation |
|---|---|---|---|---|
| 1 | 46.43 | 3.6867 | e' | |
| 2 | 46.43 | 3.6867 | e' | |
| 3 | 52.14 | 5.8466 | a2" | |
| 4 | 165.27 | 0.0000 | a1' | |
| 5 | 210.69 | 25.4830 | e' | |
| 6 | 210.69 | 25.4797 | e' |
Diagram 4: IR spectrum of TlBr3
The IR spectrum of TlBr3 was analogous to BH3 since both molecules share the same point group, D3H. The only main difference between the two spectra was that the vibrational frequencies of TlBr3 were significantly lower compared to BH3. The reason is due to mass number of Tl being 20 times larger than that of Boron and Br is much heavier than H.
Below are the Low frequencies found in the CLC09_TLBR3_FREQ.log file:
Low frequencies --- -3.4213 -0.0026 -0.0004 0.0015 3.9367 3.9367
Low frequencies --- 46.4289 46.4292 52.1449
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
E' E' A2"
Frequencies -- 46.4289 46.4292 52.1449
Red. masses -- 88.4613 88.4613 117.7209
Frc consts -- 0.1124 0.1124 0.1886
IR Inten -- 3.6867 3.6867 5.8466
Atom AN X Y Z X Y Z X Y Z
1 81 0.00 0.28 0.00 -0.28 0.00 0.00 0.00 0.00 0.55
2 35 0.00 0.26 0.00 0.74 0.00 0.00 0.00 0.00 -0.48
3 35 0.43 -0.49 0.00 -0.01 -0.43 0.00 0.00 0.00 -0.48
4 35 -0.43 -0.49 0.00 -0.01 0.43 0.00 0.00 0.00 -0.48
What is a Bond?
A bond is an inter atomic attraction, caused by net attractions and repulsions between positive (nuclei) and negative (electrons) charges. Attractive force is proportional to inter-atomic distance i.e. two atoms attract each other from far and their distance decreases to a point in which further decrease in inter-atomic distance will lead to exponential repulsion between the nuclei of the two atoms. This is well portrayed in the Lennard-Jones potential graph. A bond length is the ideal or equilibrium inter-atomic distance where the potential well lies and a bond is considered stable.
Part 3: Analysis of Isomers of Mo(CO)4L2 - Cis Trans Isomerism
First optimisation
The isomers were optimised using the DFT/B3LYP method with LANL2MB as basis set with the additional keyword opt=loose to allow faster calculation of these rough models.
trans isomer optimisation File Name = TRANSISOMEROPT File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2MB Charge = 0 Spin = Singlet E(RB3LYP) = -617.52198650 a.u. RMS Gradient Norm = 0.00116748 a.u. Imaginary Freq = Dipole Moment = 0.0000 Debye Point Group = C1 Job cpu time: 0 days 0 hours 11 minutes 42.0 seconds.
cis isomer optimisation File Name = CISISOMEROPT File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2MB Charge = 0 Spin = Singlet E(RB3LYP) = -617.52501663 a.u. RMS Gradient Norm = 0.00008743 a.u. Imaginary Freq = Dipole Moment = 8.4775 Debye Point Group = C1 Job cpu time: 0 days 0 hours 42 minutes 21.0 seconds.
The cis isomer was predicted to be more stable than the trans isomer. The dipole moment for the cis isomer was 8.4775D (large) while trans-isomer has zero dipole moment. This is due to the symmetry of the molecules.
Second optimisation
The optimised geometries were manually altered and re-optimised using the LANL2DZ basis set with the additional keywords in=ultrafine
Diagram 5: Manual alteration of isomers
modified trans isomer optimisation File Name = modtransisomeropt File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2DZ Charge = 0 Spin = Singlet E(RB3LYP) = -623.57603106 a.u. RMS Gradient Norm = 0.00002120 a.u. Imaginary Freq = Dipole Moment = 0.3029 Debye Point Group = C1 Job cpu time: 0 days 0 hours 46 minutes 43.8 seconds.
modified cis isomer optimisation File Name = modcisisomeropt File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2DZ Charge = 0 Spin = Singlet E(RB3LYP) = -623.57707196 a.u. RMS Gradient Norm = 0.00000383 a.u. Imaginary Freq = Dipole Moment = 1.3074 Debye Point Group = C1 Job cpu time: 0 days 1 hours 21 minutes 21.9 seconds.
The second alteration followed by optimisation calculated the cis to be more stable than trans. The dipole moment in modified trans isomer increased slightly from 0 to 0.3029 Debye due to loss of inversion centre after manual modification.
Bond lengths and bond angles
The isomers were investigated by comparing bond lengths and bond angles.
| Bond | Length/ Angstroms |
|---|---|
| P - Mo | 2.51210 |
| C - Mo (axial) | 2.05774 |
| C - Mo (equitorial) | 2.01172 |
| P - Cl | 2.24003 |
| C - O (axial) | 1.17566 |
| C - O (equitorial) | 1.17313 |
| Bond | Length/ Angstroms |
|---|---|
| P - Mo | 2.44483 |
| P - Cl | 2.24148 |
| C - Mo | 2.06011 |
| C - O | 1.17220 |
The bond lengths in the cis isomer were generally longer than trans isomer so as to minimise steric repulsion. The bond angle between P-Mo-P in the trans isomer is 177.475o , showing a slight deviation from ideal structure. In the cis isomer, axial bond lengths are slightly longer than equatorial bond lengths due to higher electronic density on the equatorial plane, causing axial bonds to lengthen a little to relieve electronic repulsion between bonds. The bond angle between P-Mo-P in the cis isomer is 94.152o, hinting a great steric repulsion between adjacent Cl atoms of the PCl3 group.
Vibrational analysis
IR spectrum of trans isomer
IR spectrum of cis isomer
| Vibrational mode | Frequency/ cm-1 | Intensity | Animation |
|---|---|---|---|
| 42 | 2358.94 | 1229.5456 | |
| 43 | 2359.32 | 1251.4644 | |
| 44 | 2383.27 | 22.1883 | |
| 45 | 2427.24 | 1.1796 |
| Vibrational mode | Frequency/ cm-1 | Intensity | Animation |
|---|---|---|---|
| 41 | 621.93 | 178.7990 | |
| 42 | 2359.61 | 1292.7064 | |
| 43 | 2367.49 | 632.1141 | |
| 44 | 2372.73 | 505.9990 |
The four main vibrational modes in both isomers represent carbonyl and PCl3 vibrations.
Mini Project: Aromaticity and borazine derivatives or pyridine and other group 15 substituted rings
The project focuses on several properties of two aromatic derivatives from benzene: borazine and its Group 15 substituted ring, hexachlorophosphazene. With the aid of Gaussview and SCAN, their electronic and structural properties can be examined by working out their optimised structures, molecular orbitals as well as vibrational modes.
Optimisation Analysis
The molecules were subjected to optimisation using the DFT/B3LYP method with 6-311G(d,p) as basis set.
borazine optimisation File Name = newbopt File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = 6-311G(d,p) Charge = 0 Spin = Singlet E(RB3LYP) = -242.70496965 a.u. RMS Gradient Norm = 0.00007142 a.u. Imaginary Freq = Dipole Moment = 0.0021 Debye Point Group = C1 Job cpu time: 0 days 0 hours 5 minutes 48.3 seconds.
hexachlorophosphazene optimisation File Name = newhcpopt File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = 6-311G(d,p) Charge = 0 Spin = Singlet E(RB3LYP) = -3949.61567589 a.u. RMS Gradient Norm = 0.00003326 a.u. Imaginary Freq = Dipole Moment = 0.0026 Debye Point Group = C1 Job cpu time: 0 days 0 hours 38 minutes 12.1 seconds.
| Optimised Molecule | DOI |
|---|---|
| DOI:10042/to-12078 | |
| DOI:10042/to-12079 |
Borazine bond lengths
| Bond | Bond Length/Å |
|---|---|
| B-N | 1.42980 |
| B-H | 1.19230 |
| N-H | 1.00863 |
Hexachlorophosphazene bond lengths
| Bond | Bond Length/Å |
|---|---|
| P-N | 1.59478 |
| P-Cl | 2.03782 |
Borazine angle
| Bond | Bond Angle/o |
|---|---|
| N-B-N | 117.085 |
| B-N-B | 122.914 |
| H-B-N | 121.453 |
| H-N-B | 115.538 |
Hexachlorophosphazene angle
| Bond | Bond Angle/o |
|---|---|
| N-P-N | 116.871 |
| P-N-P | 123.146 |
| Cl-P-Cl | 102.298 |
Gaussian calculated the aromatic rings to be planar (hexachlorophosphazene has protruding Cl-P-Cl bonds in and out of the phosphazene plane). The dipole moments of both molecules should have been zero since they are symmetrical. Gaussian also stated the point groups of borazine and hexachlorophosphazene to be C1, however, in actuality, they are both D3H.
Molecular Orbital Analysis
The molecular orbitals of borazine and hexachlorophosphazene were calculated using DFT/B3LYP with 6-311 d,p as basis set. (Borazine DOI:10042/to-12080 ; Hexachlorophosphazene DOI:10042/to-12081 ).
| Molecular Orbital | Borazine | Hexachlorophosphazene |
|---|---|---|
| LUMO+2 |  |

|
| LUMO+1 |  |

|
| LUMO |  |

|
| HOMO |  |

|
| HOMO-1 |  |

|
| HOMO-2 |  |

|
Energy levels/kJmol-1
| Borazine | Hexachlorophosphazene |
|---|---|
 |

|
Borazine MO analysis
Borazine may be iso-electronic with benzene, however their chemical properties differ greatly. The electron densities along the boron-nitrogen p bonds are not distributed evenly, due to the difference in electro-negativities between the two types of atoms. N is more electronegative than B. Also, the HOMO-LUMO gap is larger in borazine than benzene. Therefore, the molecular orbitals of borazine may appear lumpy in comparison to benzene, which has a smoother surface and greater degree of delocalisation in the pi system. In terms of reactivity, the polar nature of B-N bond makes borazine prone to addition reactions and therefore less stable than benzene.
Hexachlorophosphazene MO analysis
The pi-system in hexachlorophosphazene is formed via pπ(N)-dπ(P) bond while in borazine, bonding is due to pπ(N)-pπ(B). Nitrogen atoms are sp2 hybridised while phosphorus atoms are sp3 hybridised. In other words, the bonding in hexachlorophosphazene can also be described in terms of overlap between non-bonding (lone pair) of an sp2 on Nitrogen and suitable d orbitals on Phosphorus. The overlapping however may not be efficient since phosphorus is a third period element; its orbitals are larger and more diffused. Each phosphorus atom is also bonded to two other chlorine atoms; causing electron density to shift towards the chlorine atoms.
Charge distribution/ NBO analysis
Charge Distribution
| Borazine | Hexachlorophosphazene |
|---|---|
 |

|
Borazine
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
H 1 -0.09002 0.00000 1.08865 0.00137 1.09002
H 2 0.39532 0.00000 0.60182 0.00286 0.60468
H 3 -0.09002 0.00000 1.08865 0.00137 1.09002
H 4 0.39532 0.00000 0.60182 0.00286 0.60468
H 5 -0.09003 0.00000 1.08866 0.00137 1.09003
H 6 0.39533 0.00000 0.60181 0.00286 0.60467
B 7 0.74007 1.99919 2.24342 0.01732 4.25993
B 8 0.74003 1.99919 2.24346 0.01733 4.25997
B 9 0.74002 1.99919 2.24347 0.01733 4.25998
N 10 -1.04535 1.99934 6.04063 0.00537 8.04535
N 11 -1.04534 1.99934 6.04062 0.00537 8.04534
N 12 -1.04535 1.99934 6.04063 0.00537 8.04535
=======================================================================
* Total * 0.00000 11.99559 29.92364 0.08077 42.00000
Low frequencies --- 0.0005 0.0005 0.0006 9.1638 10.6639 13.3170
Low frequencies --- 290.0947 290.9810 409.1969
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A A A
Frequencies -- 290.0945 290.9800 409.1969
Red. masses -- 2.8932 2.8982 1.9058
Frc consts -- 0.1435 0.1446 0.1880
IR Inten -- 0.0002 0.0005 24.4178
Atom AN X Y Z X Y Z X Y Z
1 1 0.00 0.00 -0.19 0.00 0.00 0.66 0.00 0.00 0.53
2 1 0.00 0.00 -0.19 0.00 0.00 -0.20 0.00 0.00 0.16
3 1 0.00 0.00 0.67 0.00 0.00 -0.17 0.00 0.00 0.53
4 1 0.00 0.00 -0.08 0.00 0.00 0.27 0.00 0.00 0.16
5 1 0.00 0.00 -0.48 0.00 0.00 -0.50 0.00 0.00 0.53
6 1 0.00 0.00 0.27 0.00 0.00 -0.07 0.00 0.00 0.16
7 5 0.00 0.00 -0.16 0.00 0.00 -0.16 0.00 0.00 0.10
8 5 0.00 0.00 0.22 0.00 0.00 -0.05 0.00 0.00 0.10
9 5 0.00 0.00 -0.06 0.00 0.00 0.22 0.00 0.00 0.10
10 7 0.00 0.00 -0.07 0.00 0.00 0.23 0.00 0.00 -0.12
11 7 0.00 0.00 -0.17 0.00 0.00 -0.17 0.00 0.00 -0.13
12 7 0.00 0.00 0.23 0.00 0.00 -0.06 0.00 0.00 -0.13
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.98377) BD ( 1) H 1 - B 9
( 54.77%) 0.7401* H 1 s( 99.92%)p 0.00( 0.08%)
0.9996 0.0002 -0.0001 0.0190 0.0207
0.0000
( 45.23%) 0.6725* B 9 s( 36.64%)p 1.73( 63.32%)d 0.00( 0.04%)
-0.0007 0.6047 -0.0281 -0.0001 -0.5369
0.0213 0.0003 -0.5865 0.0232 0.0004
0.0000 0.0000 0.0000 0.0153 0.0000
0.0000 -0.0014 -0.0110
2. (1.98563) BD ( 1) H 2 - N 11
( 29.86%) 0.5465* H 2 s( 99.94%)p 0.00( 0.06%)
-0.9997 -0.0024 -0.0029 0.0076 -0.0239
0.0000
( 70.14%) 0.8375* N 11 s( 22.10%)p 3.52( 77.85%)d 0.00( 0.05%)
0.0003 -0.4699 -0.0127 -0.0001 -0.2657
-0.0029 -0.0002 0.8413 0.0093 0.0005
0.0000 0.0000 0.0000 0.0102 0.0000
0.0000 0.0145 0.0119
7. (1.98549) BD ( 1) B 7 - N 10
( 24.26%) 0.4926* B 7 s( 31.72%)p 2.15( 68.15%)d 0.00( 0.14%)
0.0001 -0.5623 -0.0310 -0.0011 -0.7996
-0.0592 0.0069 0.1948 -0.0200 -0.0118
0.0000 0.0000 0.0000 0.0152 0.0000
0.0000 -0.0240 0.0236
( 75.74%) 0.8703* N 10 s( 38.90%)p 1.57( 61.07%)d 0.00( 0.03%)
0.0001 -0.6237 0.0045 0.0000 0.7459
-0.0107 0.0000 -0.2323 -0.0170 0.0000
0.0000 0.0000 0.0000 0.0061 0.0000
0.0000 -0.0117 0.0117
Both B and N showed sp2 hybridised characteristics.
Hexachlorophosphazene
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
P 1 1.79597 9.99722 3.06224 0.14457 13.20403
P 2 1.79597 9.99722 3.06223 0.14458 13.20403
P 3 1.79594 9.99722 3.06227 0.14457 13.20406
Cl 4 -0.19468 9.99972 7.18147 0.01349 17.19468
Cl 5 -0.19467 9.99972 7.18145 0.01349 17.19467
Cl 6 -0.19466 9.99972 7.18145 0.01349 17.19466
Cl 7 -0.19473 9.99972 7.18152 0.01349 17.19473
Cl 8 -0.19469 9.99972 7.18147 0.01349 17.19469
Cl 9 -0.19472 9.99972 7.18151 0.01349 17.19472
N 10 -1.40659 1.99924 6.39148 0.01586 8.40659
N 11 -1.40653 1.99924 6.39142 0.01586 8.40653
N 12 -1.40661 1.99924 6.39150 0.01586 8.40661
=======================================================================
* Total * 0.00000 95.98774 71.45002 0.56223 168.00000
Low frequencies --- -5.6811 -4.7168 -2.7366 0.0033 0.0047 0.0049
Low frequencies --- 35.6850 36.6647 37.4110
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A A A
Frequencies -- 35.6608 36.6531 37.3885
Red. masses -- 29.2414 29.0029 29.0599
Frc consts -- 0.0219 0.0230 0.0239
IR Inten -- 0.0030 0.1686 0.1483
Atom AN X Y Z X Y Z X Y Z
1 15 0.00 0.00 -0.05 0.00 0.00 -0.14 0.00 0.00 -0.05
2 15 0.00 0.00 0.06 0.00 0.00 -0.11 0.00 0.00 -0.10
3 15 0.00 0.00 -0.05 0.00 0.00 -0.06 0.00 0.00 -0.14
4 17 0.34 -0.17 0.08 0.17 0.35 0.17 0.11 -0.06 -0.01
5 17 -0.34 0.17 0.08 -0.17 -0.35 0.17 -0.11 0.06 -0.01
6 17 0.26 0.27 0.09 0.11 0.08 0.00 0.28 -0.28 0.17
7 17 -0.26 -0.27 0.09 -0.11 -0.08 0.00 -0.28 0.28 0.17
8 17 -0.03 0.21 -0.13 -0.22 -0.28 0.10 0.33 -0.17 0.10
9 17 0.03 -0.21 -0.13 0.22 0.28 0.10 -0.33 0.17 0.10
10 7 0.00 0.00 -0.45 0.00 0.00 -0.20 0.00 0.00 -0.18
11 7 0.00 0.00 0.18 0.00 0.00 0.01 0.00 0.00 -0.49
12 7 0.00 0.00 0.19 0.00 0.00 -0.49 0.00 0.00 0.04
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
3. (1.97624) BD ( 1) P 1 - N 10
( 29.59%) 0.5439* P 1 s( 29.73%)p 2.31( 68.78%)d 0.05( 1.49%)
0.0000 -0.0001 -0.5451 -0.0138 0.0015
-0.0001 -0.0003 -0.7911 -0.0251 -0.0142
0.0038 0.0002 0.2441 0.0387 0.0085
-0.0013 0.0000 0.0004 0.0000 0.0000
0.0000 0.0546 0.0001 0.0000 -0.0934
0.0563
( 70.41%) 0.8391* N 10 s( 35.62%)p 1.81( 64.33%)d 0.00( 0.05%)
0.0005 -0.5968 0.0058 0.0004 0.7633
0.0097 0.0052 -0.2459 0.0061 0.0022
-0.0004 0.0000 0.0000 0.0185 0.0000
0.0000 -0.0062 0.0129
5. (1.81615) BD ( 2) P 1 - N 12
( 7.54%) 0.2745* P 1 s( 0.00%)p 1.00( 58.60%)d 0.71( 41.40%)
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0004 0.0000 0.0000
0.0000 0.0000 -0.0002 0.0000 0.0000
0.0000 0.0014 0.7450 -0.0918 0.1502
0.0027 0.0002 0.1742 0.6194 0.0002
0.0002
( 92.46%) 0.9616* N 12 s( 0.00%)p 1.00( 99.90%)d 0.00( 0.10%)
0.0000 0.0001 0.0000 0.0000 0.0005
0.0000 0.0000 -0.0002 0.0000 0.0000
0.9995 -0.0015 -0.0038 0.0000 0.0290
-0.0114 0.0000 0.0000
The states of hybridisation in hexachlorophosphazene was mixed. First, Nitrogen showed sp2 hybridised characteristics (s(35.62%),p(64.33%)). Same goes for phosphorus (s(29.73%), p(68.78%)). Then nitrogen displayed a p-orbital (p(99.9%)) while the phosphorus showed a p-d orbital (p(58.60%),d(41.40%)). As a conclusion, P-N bonding is more complex than C-C (in benzene) or B-N (in borazine) due to d-orbitals in phosphorus. This allows the molecule to form bonds with greater flexibility in hybridisation, and can ultimately stabilise the molecule.
Vibrational analysis
The main focus is on major peaks found in the Infrared spectrum of each molecule respectively. (Borazine DOI:10042/to-12083 ; Hexachlorophosphazene DOI:10042/to-12084 ).
Borazine
IR spectrum of borazine
| Vibrational mode | Frequency/cm-1 | Intensity | Animation | Symmetry Point Group |
|---|---|---|---|---|
| 3 | 409.20 | 24.4178 | a2" | |
| 8 | 731.42 | 55.0096 | a2" | |
| 12 | 936.13 | 206.4862 | a2" | |
| 23 | 1484.29 | 478.7627 | e' | |
| 24 | 1484.53 | 478.8746 | e' | |
| 25 | 2609.25 | 295.2443 | e' | |
| 26 | 2609.58 | 295.1188 | e' |
Hexachlorophosphazene
IR spectrum of hexachlorophosphazene
| Vibrational mode | Frequency/cm-1 | Intensity | Animation | Symmetry Point Group |
|---|---|---|---|---|
| 19 | 505.61 | 359.0475 | Animate | e' |
| 20 | 505.93 | 359.0075 | Animate | e' |
| 23 | 607.14 | 666.4233 | Animate | a2" |
| 29 | 1224.74 | 1334.0027 | Animate | e' |
| 30 | 1224.97 | 1334.7555 | Animate | e' |
Analysis
Coincidently, both borazine and hexachlorophosphazene contain 12 atoms; therefore the total number of vibrational modes = 3N-6 = 3(12)-6 = 30. Borazine has more vibrations with high intensities than hexachlorophosphazene. Generally, the frequencies of vibrations for hexachlorophosphazene are lower than borazine due to presence of heavier atoms like phosphorus and chlorine.
Conclusion
The mini project can be further studied by investigating other inorganic four membered rings i.e. disulfur dinitride (a precursor of a low temperature superconductor, polythiazyl[3]) or other isoelectronic derivatives of borazine[4] and phosphazene[5]. The isoelectronic nature of benzene and borazine have been rationalised through optimisation, molecular and vibrational analyses. However, hexachlorophosphazene can be modified and studied again i.e. substituting Cl atoms with other halogens or R=alkyl or aryl groups to gain a better understanding on its bonding and hybridisation. Overall, the project achieved its requirements.
References
- ↑ M.S. Schuurman, W.D. Allen, H.F. Schaefer III, "The ab initio limit quartic force field of BH3", J. Comp. Chem., 2005, 26 (11), 1106-1112DOI:10.1002/jcc.20238
- ↑ M. Atanasov, D. Reinen, J. Phys. Chem. A, 2001, 105 (22), 5467 DOI:10.1021/jp004511j
- ↑ Chem. Rev., 1979, 79 (1), pp 1–15DOI:10.1021/cr60317a002
- ↑ J. Am. Chem. Soc., 1958, 80 (17), pp 4515–4517DOI:10.1021/ja01550a020
- ↑ M. J. S. Dewar, P. A. Marr, "A Derivative of Borazarene", J. Am. Chem. Soc., 1962, 84, 3782DOI:10.1021/ja00878a045