Rep:Mod:clc09

Module 1

Modelling using Molecular Mechanics

1.1 The Hydrogenation of Cyclopentadiene Dimer

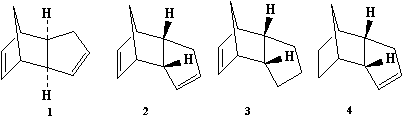
The dimerization of cyclopentadiene occurs readily at room temperature and is an example of a Diels-Alder cycloaddition reaction. However, the endo isomer (2) is formed preferentially over the exo isomer (1). Hydrogenation of the endo isomer (2) yields two possible dihydro derivatives (3) and (4). Utilising molecular mechanics computations, all four species (1) to (4) are subjected to the same computational treatment to gain an understanding of the regioselectivity and their energetic stabilities.

Diagram 1: (1) exo isomer; (2) endo isomer; (3) & (4) dihydro derivatives of endo isomer

Result

The table below summarizes the geometries and energy values estimated by MM2 in ChemBio3D Ultra.

	(1) Exo isomer	(2) Endo isomer	(3) Dimer 3	(4) Dimer 4
Stretch	1.2852	1.2506	1.2779	1.0966
Bend	20.5800	20.8487	19.8614	14.5215
Stretch-Bend	-0.8380	-0.8352	-0.8346	-0.5498
Torsion	7.6560	9.5103	10.8087	12.4968
Non-1,4 VDW	-1.4177	-1.5422	-1.2229	-1.0669
1,4 VDW	4.2335	4.3180	5.6324	4.5134
Dipole - dipole	0.3775	0.4474	0.1621	0.1406
Total energy, kcalmol-1	31.8765	33.9976	35.6850	31.1521

Discussion

From MM2 calculation, the total energy of the exo isomer is lower than the endo isomer and they differ by 2.1211 kcalmol^-1; meaning the exo isomer is thermodynamically more stable than the endo one. Since a majority of the products is in the endo form, it is safe to deduce that dimerization of cyclopentadiene proceeds under kinetic control. The pathway leading to the endo isomer has a lower energy transition state than the exo one. However, the main energy difference between endo and exo isomer is due to torsion energy. The endo isomer has larger torsion energy than the exo isomer. This can be visualised as closer proximity of the two large carbon rings in the endo isomer, leading to larger torsional strain. Dimer 4 has a lower total energy than dimer 3 by 4.5329 kcalmol^-1. This is due to the noticeable difference in bend energies between the two dihydro derivatives. Dimer 3 has a larger bend energy due to the great ring strain exerted on the only C=C bond in the molecule. The ideal bond angle for sp² hybridised C=C bond is 120^o. In dimer 3, the bond angle about the C=C is less than 120^o (~ 100^o). In dimer 4, the angle about C=C bond is slightly wider and the ring strain is more tolerable.

1.2 Stereochemistry and Reactivity of an Intermediate in the synthesis of Taxol

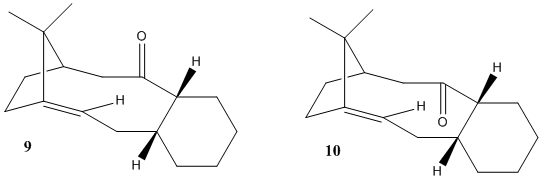
Taxol is a vital drug for the treatment of ovarian cancers. En route its total synthesis, a key intermediate (9) or (10) is formed and when left standing, it displays atropisomerism by conversion into an alternative carbonyl isomer. They are formed from an oxy-Cope rearrangement . The stereochemistry of carbonyl addition depends on which isomer is more stable and this is where computational chemistry comes into practice. The atropisomers were first modelled using ChemBio3D, followed by calculation of their energies using MM2 and MMFF94 molecular mechanics models accordingly.

Diagram 2: Atropisomers (9) and (10) of an intermediate during the total synthesis of Taxol

MM2 molecular mechanics model Result

	Isomer 9 Chair Conformation	Isomer 10 Chair Conformation
Stretch	2.7837	2.6195
Bend	16.5396	11.3393
Stretch-Bend	0.4303	0.3431
Torsion	18.2478	19.6756
Non-1,4 VDW	-1.5453	-2.1654
1,4 VDW	13.1082	12.8731
Dipole - dipole	-1.7247	-2.0023
Total energy, kcalmol-1	47.8396	42.6829

MMFF94 molecular mechanics model Result

	Isomer 9 Chair Conformation	Isomer 10 Chair Conformation
Total energy, kcalmol-1	70.5409	60.5651

Discussion

Based on MM2 and MMFF94 models, Isomer 10 with its cyclohexane ring in a chair conformation has the lowest total energy. Hence, Isomer 10 is expected to predominate in a mixture of intermediates and will experience very high frequency of attacks on the carbonyl group via this conformation. The stability of isomer 10 can be traced back to the anti-peri-planar molecular orbitals overlap between σ(C-H) and π*(C=O). Additionally, atropisomers 9 and 10 are good examples of hyper stable olefins; meaning the alkene is less strained than the resulting alkane after hydrogenation.

Modelling Using Semi-empirical Molecular Orbital Theory

1.3 Regioselective Addition of Dichlorocarbene

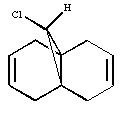
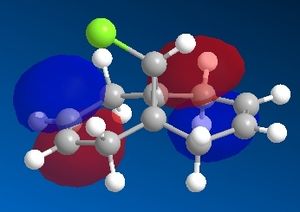
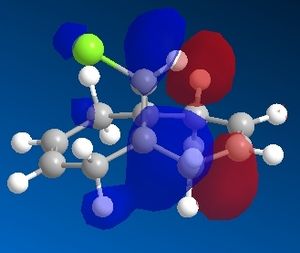
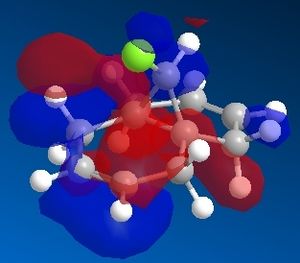
Dichlorocarbene reacts with alkenes i.e. compound 12 via [1+2] cycloaddition to form dichlorocyclopropanes. However, compound 12 contains two C=C bonds; one anti and another syn to the C-Cl bond. The aim is to rationalise the nucleophilicty of each C=C bond. In addition to molecular mechanics, molecular orbital calculations will be employed here. Firstly, the energy of compound 12 will be minimised using MM2, in order to prepare it for MO calculation using MOPAC method. The wavefunction of each MO will be calculated and its resulting MO surfaces will be plotted accordingly.

Diagram 3: Structure of compound 12

Result

Contour plots of resulting molecular orbitals

LUMO +2

LUMO +1

LUMO

HOMO

HOMO -1

Discussion

Based on the contour plots, the HOMO displayed high electron density on the π (C=C) bonding orbital syn to the C-Cl bond; hence, it is most susceptible to electrophilic attack, while neglecting steric effects. Whereas on the LUMO, a large π* anti-bonding orbital is seen on the C=C bond syn to the C-Cl bond; more susceptible to nucleophilic attack.

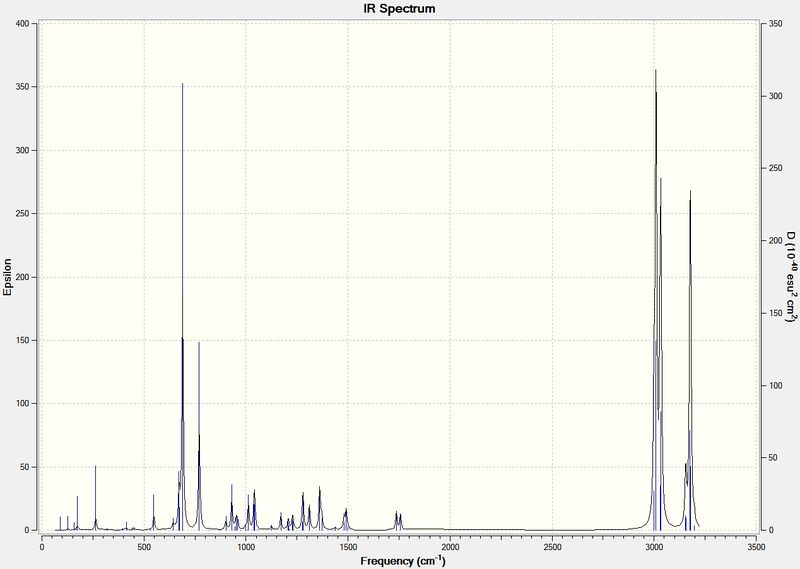
The Infrared spectra for compound 12 and its dihydro derivative were produced using the density functional approach with Gaussian.

IR spectrum of Compound 12

Stretching frequencies

C-Cl vibration: 770.89 cm^-1

Anti C=C vibration: 1737.06 cm^-1

Syn C=C vibration: 1757.35 cm^-1

IR spectrum of Dihydro derivative

Stretching frequencies

C-Cl vibration: 774.88 cm^-1

Syn C=C vibration: 1758.09 cm^-1

1.4 Monosaccharide chemistry: glycosidation

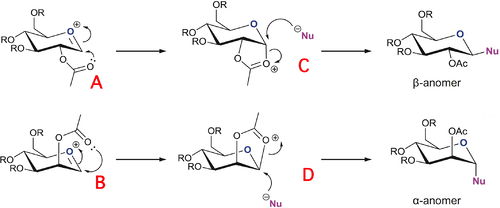
Glycosidation involves replacing the group X by reaction with a nucleophile, Nu. The two sugars shown below give different anomers depending on the orientation of the OAc group on the adjacent carbon. The adjacent acetyl group exerts an effect known as the neighbouring-group-participation. For the β-anomer, the intermediate oxonium cation must be attacked from the bottom face, so that the incoming nucleophile can replace it from the top face. Likewise, the α-anomer is formed by the acetyl oxygen attacking from the top face of the oxonium cation, allowing the nucleophile to come in from the bottom face.

The aim is to model these facial preferences, i.e. the diastereospecificity, using both MM2 and MOPAC/PM6 methods. As for the R group, a methyl group was an ideal choice since –OMe is a common protecting group in carbohydrate chemistry. Also, the R group should not be too large as it may cause steric problems and calculations involving large R groups will consume much more time. R=H was also avoided for fear of unwanted hydrogen bonding interactions between hydroxyl groups.

Diagram 4: Reaction scheme for synthesis of different anomers

MM2 molecular mechanics model Result

[ ' ] sign denotes acyl group is pointing above or below the plane of the oxonium cation

	A	A'	B	B'	C	D
Stretch	2.2725	2.3961	2.3969	2.1430	1.9928	1.7770
Bend	9.8712	12.8506	9.7581	12.4604	13.0852	18.4088
Stretch-Bend	0.8780	1.0410	0.8684	0.9203	0.6842	0.7354
Torsion	1.0281	2.5098	0.3718	1.0398	7.4478	7.8704
Non-1,4 VDW	-2.1959	-3.0718	-2.4633	-3.7076	-2.5325	-3.4128
1,4 VDW	18.7460	18.7637	18.6772	18.8368	17.7238	17.6179
Charge - dipole	-7.9286	2.9693	-4.4082	-0.9954	-10.5043	-7.1139
Dipole - dipole	3.7630	4.7346	4.2204	5.8594	-0.5354	-2.0222
Total energy / kcalmol-1	26.4342	42.1934	29.4213	36.5567	27.3616	33.8606

The geometries and energies above were predicted with MM2 first. However, the model was incomplete since MM2 molecular model does not take into account the effects of neighbouring-group-participation, as well as electronic effects. Moreover, anomeric effect is a stereoelectronic phenomenon, and cannot be explained solely based on steric consideration. Therefore, the MOPAC/PM6 method is used in order to provide a better stereoelectronic treatment.

MOPAC/PM6 molecular mechanics model Result

	A	A'	B	B'	C	D
Heat of formation / kcalmol-1	-77.09295	-67.69936	-75.84843	-64.08252	-91.66341	-88.51611
RMS Gradient	0.06959	0.08026	0.09175	0.08454	0.05739	0.09224

Structure based Mini project using DFT-based Molecular orbital methods

Assigning regioisomers in "Click Chemistry"

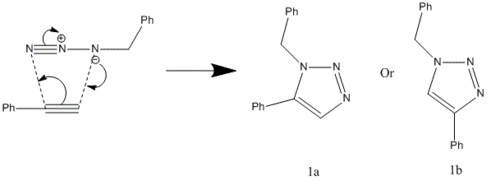
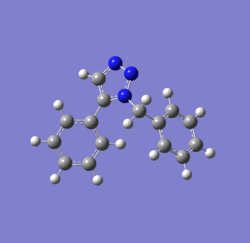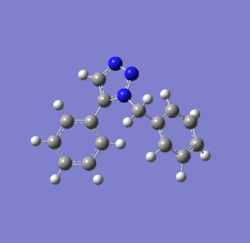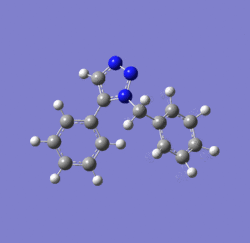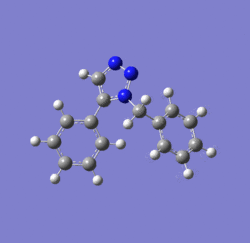
In 2002, Nobel Laureate K. Barry Sharpless introduced the notion of ‘click chemistry’, which seeks to exploit reactions which “are tailored to generate substances quickly and reliably by joining small units together”. ‘Click reaction’ is regioselective depending on the catalyst used. When mono-substituted alkynes and azides are used, they react via 1,3 polar cycloaddition to form two possible regioisomeric di-substituted 1,2,3-triazoles. Interestingly, under Ru(II) catalysis the 1,5-isomer A forms but when Cu(I) is used the 1,4-isomer B forms. The objective of this investigation is to tell apart these isomers spectroscopically. The example used here is taken from literature in Table 1, entry 1.

Mechanism of 'Click reaction'

MM2 molecular mechanics model Result

	Isomer 1a	Isomer 1b
Stretch	1.1062	0.7739
Bend	18.2996	13.1031
Stretch-Bend	0.1077	-0.0298
Torsion	-15.7201	-14.8218
Non-1,4 VDW	0.7208	-1.6863
1,4 VDW	14.3720	14.7260
Dipole - dipole	-1.6631	-1.4087
Total energy, kcalmol-1	17.2230	10.6564

MM2 model predicted Isomer 1b to be more stable than Isomer 1a. This is due to the notable difference in bend energies between 1a and 1b.

MOPAC/AM1 molecular mechanics model Result

	Isomer 1a	Isomer 1b
Heat of formation / kcalmol-1	143.45285	142.12898
RMS Gradient	0.08369	0.08524

For Isomer 1a, the MOPAC/AM1 model is similiar to the MM2, except this time the phenyl ring is no longer co-planar with the triazole; it is tilted along the triazole plane by an angle of ~27^°.

The same goes for Isomer 1b; the MOPAC/AM1 model is nearly identical with the MM2 with the exception of the phenyl ring tilting by 2^° along the triazole.

Refined geometries using DFT=mpw1pw91 method

Isomer 1a	Isomer 1b

NMR spectra

The following NMR calculations were obtained using DFT mpw1pw91/ 6-31G(d,p) and retrieved via SCAN. The spectra were then viewed using Gaussian.

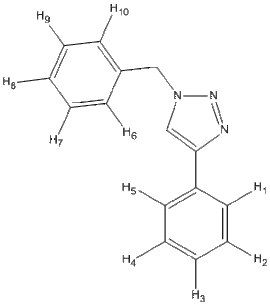
Isomer	Carbon Framework & Labels	13C NMR	1H NMR	N NMR	DOI
1a					DOI:10042/to-11773
1b		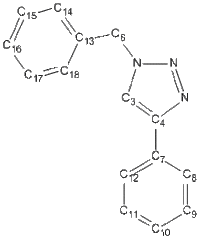			DOI:10042/to-11774

¹³C NMR of Isomer 1a ( Chloroform ) δ/ppm

Gaussian value	Integral	Assignment
59.9238	1	C3
62.4896	1	C13
67.9713	1	C4
70.3621	1	C8
70.7149	1	C10
70.9790	1	C9
71.1034	1	C17
71.1151	2	C12
71.4026	1	C15
71.5241	1	C11
71.8951	1	C7
72.1117	1	C16
72.9212	1	C18
73.1892	1	C14
144.3464	1	C6

¹³C NMR of Isomer 1b ( Chloroform ) δ/ppm

Gaussian value	Integral	Assignment
51.7409	1	C4
63.3733	1	C13
68.8724	1	C7
71.0373	1	C17
71.3800	1	C9
71.6221	1	C11
71.7772	1	C15
71.7781	2	C16
72.0629	1	C14
72.3593	1	C18
72.4554	1	C10
74.7112	1	C8
75.2756	1	C12
79.6103	1	C3
141.7195	1	C6

³J H-H couplings

The following ³J H-H couplings were predicted by Janocchio,

Diagram 5: Isomer 1a

³J H-H coupling for Isomer 1a

Hydrogen Pair	Coupling Constant /Hz	Dihedral Angle /o
1-2	8.2184	0.8
2-3	8.2198	0.3
3-4	8.2191	0.6
4-5	8.2153	0.3
6-7	8.2199	0.0
7-8	8.2199	-0.1
8-9	8.2199	-0.1
9-10	8.2195	-0.4

Diagram 6: Isomer 1b

³J H-H coupling for Isomer 1a

Hydrogen Pair	Coupling Constant /Hz	Dihedral Angle /o
1-2	8.2200	0.0
2-3	8.2200	0.0
3-4	8.2200	0.0
4-5	8.2200	0.1
6-7	8.2200	0.1
7-8	8.2200	-0.1
8-9	8.2200	-0.1
9-10	8.2200	0.1

Infrared Spectra

Isomer 1a	Isomer 1b

Assignment	Isomer 1a wave number /cm-1	Isomer 1a Animation	Isomer 1b wave number /cm-1	Isomer 1b Animation
C-H stretch (benzyl ring)	743.49		744.03
N-N stretch (triazole)	1282.54		1309.30
C=C stretch (phenyl ring)	1662.47		1665.87
C=C stretch (benzyl ring)	1662.01		1663.48
CH2 stretch	3130.66		3122.76
C-H stretch (triazole)	3275.88		3295.37

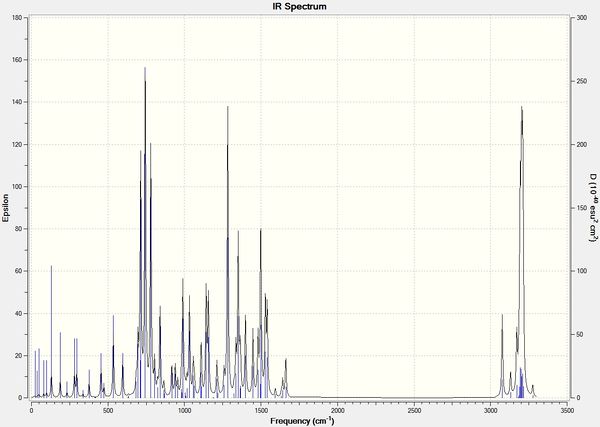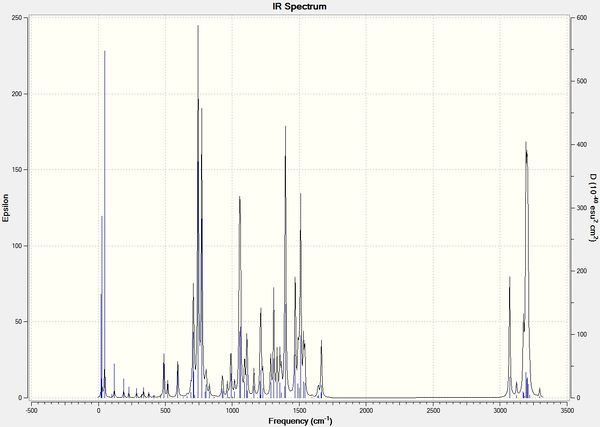
Sum of electronic and thermal Free Energies

The free energies of the isomers were predicted by DFT:

Isomer 1a: ΔG= -742.81 kJmol^-1

Isomer 1b: ΔG= -742.84 kJmol^-1

Further Tests

Optical Rotation: since both Isomers 1a and 1b lack any chiral centers, investigation via optical rotation is omitted.

Circular Dichroism spectroscopy: the NMR and IR spectra are sufficient indicators to distinguish between isomers 1a and 1b. Hence, no further optical method required.

Conclusion

Various spectroscopic methods can be estimated by DFT. The IR method was efficient in differentiating the isomers i.e. distinct vibrations found on different isomers. The project can be further studied by investigating (a) varying functional groups for R1 and R2 on the IR spectra, (b) frontier molecular orbitals of isomers and their reactivity, regio-selectivity, stereo-selectivity etc., and (c) verifying the magnitude of error in NMR i.e. different solvents used may cause deviation from actual value. For example, Literature uses CDCl₃ while Gaussian calculations used CHCl₃. Overall, the investigation was satisfactory.