Rep:Mod:ckw08
Introduction
In this course, molecular mechanics and various other computational methods are used to predict various properties of molecules and reactions. It is a very powerful tool as it can distinguish between various reaction mechanisms via optimalisation of intermediates or products, it can help identify your product by calculating various spectroscopic data to a high degree of accuracy and the list goes on. We were given various problems and using such computational methods, I shall endeavour to solve them to gain an understanding in the specific problems.
The Hydrogenation of Cyclopentadiene
Dimer Formation
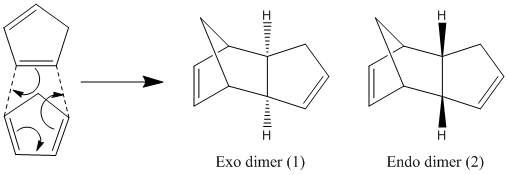
Cyclopentadiene can readily dimerise at room temperature to form one of two possible products, the exo and endo dimers. The endo dimer is specifically produced[1]. Using Chem3D, both dimers were defined and their geometries optimised using the MM2 force field. The following energies were calculated for the dimers, table 1.
| Dimer | ||
| Stretch | 1.2952 | 1.2454 |
| Bend | 20.5605 | 20.8603 |
| Stretch-Bend | -0.8409 | -0.8320 |
| Torsion | 7.6710 | 9.5039 |
| Non-1,4 VDW | -1.4226 | -1.5083 |
| 1,4 VDW | 4.2457 | 4.3012 |
| Dipole | 0.3777 | 0.4448 |
| Total energy (kcal/mol) | 31.8867 | 34.0153 |
The data shows that the exo dimer is more stable in comparison with the endo dimer. This suggests that the exo dimer is the thermodynamic product of the dimerisation of cyclopentadiene, but due to the endo dimer being predominantly produced, the reaction must be under kinetic control. Secondary orbitals interactions give rise to the kinetic control, providing a route of lower activation energy to the endo dimer[2]. On heating, the exo form would be more favourable to form due to more cyclopentadiene having the required energy to cross the higher energy transition state. So the product with the lowest energy would form, i.e. the exo dimer.
Endo Dimer Hydrogenation
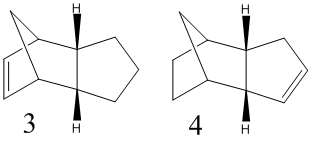
Hydrogenation of the endo dimer of cyclopentadiene initially gives one of the dihydro derivatives 3 and 4. Only after prolonged hydrogenation would the tetrahydro derivative be formed. Again using Chem3D and the MM2 force field, structure 3 and 4 can be analysed to determine which would be the most thermodynamically favoured.
 |
 |
 |
| Dihydro derivative | ||
| Stretch | 1.2685 | 1.1014 |
| Bend | 19.8502 | 14.5271 |
| Stretch-Bend | -0.8330 | -0.5459 |
| Torsion | 10.8085 | 12.5093 |
| Non-1,4 VDW | -1.2037 | -1.0568 |
| 1,4 VDW | 5.6498 | 4.4961 |
| Dipole | 0.1621 | 0.1406 |
| Total energy (kcal/mol) | 35.7025 | 31.1718 |
Comparing the 2 overall energies of the dihydro derivatives, product 4 is the most thermodynamically stable, being as it is lower in energy, in comparison to product 3. Therefore, product 4 would be the expected product for this reaction. Comparing the different energy contribution, the stretch, stretch-bend, non-1,4 VDW and dipole energies are relatively similar, only different slightly for the 2 products. There is a larger difference between the torsion and 1,4 VDW energies, but the significant differences are between the bend and torsion energies and these would dictate the relative stabilities of the products. The main issue in the selectivity of this reaction is the bridging carbon and the relative position of the unsaturated bonds. The unsaturated bond in product 3 in considerably closer to the bridge. This would result in the molecule being significantly more strained than product 4. Note there is no Hydrogen bonding term.
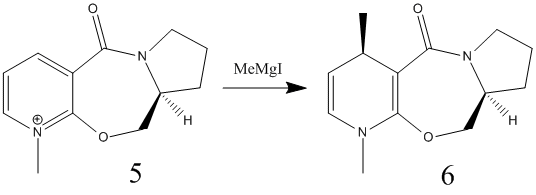
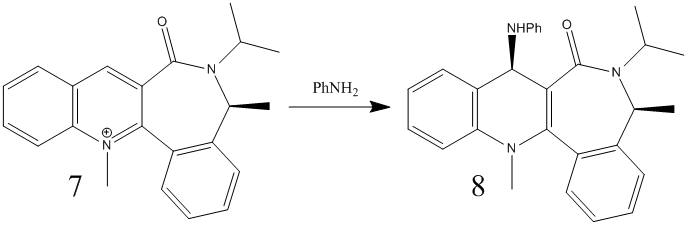
Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)
Using molecular mechanics, the stereocontrol of reactions can be predicted. The following two addition reactions give stereospecific products and using molecular mechanics the products can be predicted in terms using the lowest energy geometry of reactants. Using such a method can also determine how a reaction occurs if the products are known.
 |
 |
The reactants were modelled on Chem3D and their structures were optimized as before. For reactant 5, various starting points for the optimisation were used and the resultant energies were noted.
| Starting configuration | End configuration | Minimized energy (kcal/mol) | Carbonyl dihedral angle (degrees) |
| 43.1386 | 11.2457 | ||
| 44.6084 | 11.8527 | ||
| 44.6234 | 11.4180 |
As you can see from the above table, the geometry was optimized to very similar structures, but not the same. The differences between the final energy minimized structures was in the conformation of the 5 member ring.
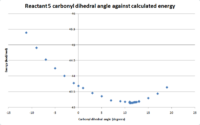
Another factor to consider when looking for the lowest energy conformer is the dihedral angle of the carbonyl in relation to the pyridinium ring and the reaction centre where the nucleophilic addition occurs. To investigate this, the lowest energy conformation of the 5 membered ring determined above was used, then the dihedral angle was fixed at various angles and the energy was minimized then noted. The results, shown in figure 7. The optimum dihedral angle for the carbonyl group was determined to be approximately 11o. MeMgI cannot be included in the calculations due to error messages arising from the program not having the capability to deal with the magnesium atom.
Now that the geometry of the reactant is determined, the stereochemistry of the reaction can be explained. The methyl group has be added to the pyridinium ring so that it comes out of the plane of the page, which is the same as the carbonyl group. For this reaction, the magnesium, being electropositive, coordinates to the electronegative oxygen of the carbonyl group. The methyl then attacks the ring, but crucially, on the same side of the ring that the carbonyl group is pointing. Since the carbonyl group is pointing out of the plane of the page, the methyl group adds to the ring in the same geometry. The halogen coordinates to the bridging oxygen which in turn stabilises the molecule during the reaction[3].
The same method was applied to reactant 7. Table 4 shows the variation in energies on changing the geometry on the molecule.
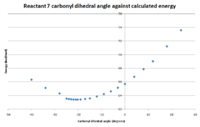
| Starting configuration | End configuration | Minimized energy (kcal/mol) | Carbonyl dihedral angle (degrees) |
| 63.4669 | -20.1053 | ||
| 63.4876 | -20.3853 | ||
| 63.4573 | -21.0007 |
As before, the energy minimized structures gave similar results even on changing the initial geometries. The carbonyl dihedral angle differed slightly in each. Again, the angle was changed periodically and the results are shown in figure 8. The angle that gave the minimal energy for reactant 7 was approximately 20o. The main difference with this reactant it that the angle is negative. This means that the carbonyl is no longer coming out of the plane of the screen, but in fact going in. Product 8 shows the added group coming out of the plane of the screen, opposite to that of the carbonyl group. This indicates a different mechanism in comparison the the previous reaction. The reaction occurs via the nucleophile attacking the para position of the pyridinium ring on the least hindered face. Since the carbonyl is on the bottom face, the nucleophile attacks from above. The steric bulk of the nucleophile dominates the stereo selectivity of this reaction, in agreement with literature[4]. The main reason why the attack is on the opposite side to the carbonyl is that the nucleophile contains a nitrogen and would be repelled by the carbonyl oxygen since both are electron rich.
Improvements
A way to improve the above calculations would be to involve all the reactants in the same model and observe the minimized energy structure. This could shed light on the mechanism as it might show a variation not predicted. Another way would be to calculate the orbitals involved in the reaction and their relative geometry. This also could show how particular stereo selectivities are favoured over others.
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
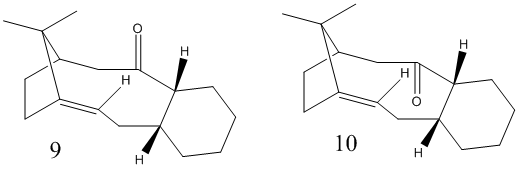
In the synthesis of Taxol, there is a key intermediate, but there are two possible geometries, 9 or 10. Using MM2 and MMFF94 calculations, predictions on the structure of the intermediate can be made. An important aspect is not only which direction the carbonyl group is pointing, but also the conformation of the adjoining hexane ring. For each isomer, there were chair, boat and twist-boat conformations. The rest of the molecule, to the left of the carbonyl group, is fixed in position due to the alkene connected to one end of the bridge. Tables 5 shows the results of the this investigation.
| Geometry | ||||||||
| Minimized energy (kcal/mol) MM2 | 41.8088 | 54.4478 | 46.3812 | 46.5309 | 53.0751 | 58.7141 | 57.0596 | 56.9397 |
| Minimized energy (kcal/mol) MMFF94 | 60.6612 | 79.3052 | 65.3812 | 63.9281 | 74.7745 | 81.6308 | 80.3690 | 79.2264 |
It was found that for both the intermediates, that the chair conformation was the favoured geometry for the hexane ring, but each had a different direction. In intermediate 9, the ring would be in plane and in line with the rest of the molecule, while in 10, the ring would be pointing the same direction of the carbonyl, i.e. down. The various twist boat conformations were all higher in energy than their corresponding chair conformations, but intermediate 9 was found to have the lower energy, so this would be the expected intermediate in the reaction.
When comparing methods, i.e. MM2 and MMFF94, they both reach the same conclusion, but differ slightly when energies are close to each other, for example when comparing different twist boat structures, 9 twist 2 and 3. This illustrates that there are minor differences between the methods, but this did not impact on the final result.
It has been observed that the alkene extremely stable and reacts abnormally slow. This is due to the alkene being hyperstable and inert to hydrogenation [5]. Hyperstable alkenes are observed when there is considerable less strain the when the alkene bond is present in comparison to if it were a regular C-C bond. In this system, the bridge makes the system hyperstable since it is unfavoured to hydrogenate and increase the strain. This is common for bridged molecules, where the alkene is at the head, but not true for all cases.
Modelling Using Semi-empirical Orbital Theory
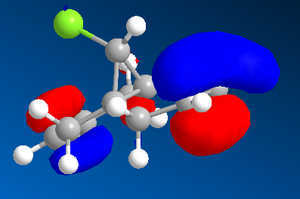
In this section, the molecular orbitals of dichlorocarbene are analysed to help understand the reactivity of the compound, in particularly the alkene bonds. Below are the MO's calculated using the MOPAC calculations in Chem3D.
 |
 |
 |
 |
 |
As you can see from the above MO diagrams, the HOMO shows high electron density on the syn-alkene, which would indicate that this species would react as an electrophile. It is also worth noting that there is a potential interation between the HOMO -1 and the LUMO +1, where the lobes from the C-Cl antibonding orbitals constructively overlap with the pi bonds of the alkenes. This stabilises the the HOMO -1 [6].
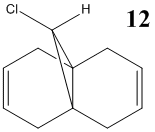
Vibrational Calculations
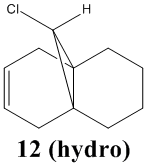
In this section the vibrational frequencies of the C-Cl and alkene bonds were calculated for structure 12, and also for its anti-alkene hydrogenated form, 12 (hydro). Below are the results of the calculations:
| Bond | Structure 12 /cm-1 | Structure 12 (hydro) /cm-1 | Literature value /cm-1[7] |
| Syn-alkene C=C | 1757.43 | 1758.05 | 1620-1680 |
| Anti-alkene C=C | 1737.00 | N/A | 1620-1680 |
| C-Cl | 770.83 | 774.95 | 600-800 |
When comparing the IR stretches of the two compounds, the strengths of both the alkene and C-Cl bond have increased in the hydrogenated molecule. This would be due to the interation stated earlier. There is less of an overlap, so the C-Cl bond would be stronger. Also, since there would be more electron density in the C-Cl region, there would be more donated in to the pi bonding orbital of the remaining alkene bond.
Mini Project: The total synthesis of (-)Cubebol
Unfortunately, I have run out of time to write up fully but shall endeavour to finish asap. I have the caluclations but I still need to write up.
My NMRS are:
Structure 17: http://hdl.handle.net/10042/to-6486 Structure 18: http://hdl.handle.net/10042/to-6487 Structure 19: http://hdl.handle.net/10042/to-6488
References
- ↑ W.L. Jorgensen, D. Lim and J.F. Blake, J. Am. Chem. Soc., 1993, 115, 2936-2942. DOI:10.1021/ja00060a048
- ↑ P. Caramella, P. Quadrelli and L. Toma, J. Am. Chem. Soc., 2002, 124, 7, 1130-1131. DOI:10.1021/ja016622h
- ↑ A.G. Schultz and L. Flood, J. Org. Chem, 1986, 51, 838-841, DOI:10.1021/jo00356a016
- ↑ S. Leleu, C. Papamicael, F. Marsais, G. Dupas and V. Levacher, Tetrahedron: Asymmetry, 2004, 15, 3919-3928.DOI:10.1016/j.tetasy.2004.11.004
- ↑ W. F. Maier and P. Schleyer, J. Am. Chem. Soc., 1981, 103 1891
- ↑ B. Halton, R. Boese and H. S. Rzepa, J. chem. Soc., Perkin Trans 2, 1992, 447. DOI:10.1039/P29920000447
- ↑ http://www2.ups.edu/faculty/hanson/Spectroscopy/IR/IRfrequencies.html
