Rep:Mod:ckl2111C

The Hydrogenation of a Cyclopentadiene Dimer

Dimerisation of cyclopentadiene

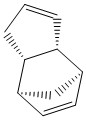
The dimerisation of two cyclopentadiene rings forms two possible products, an endo and an exo isomer. The energies and stabilities of both isomers is calculated using the MMFF94 force field in the ChemBio3D program and this is used to predict which isomer will be the most stable. The dicyclopentadiene forms a norbornane-type structure with bridgehead carbons on one of the rings.

Cyclopentadiene exo dimer 1 and endo dimer 2

Cyclopentadiene exo dimer 1

Cyclopentadiene endo dimer 2

2D structure of the optimised exo dimer 1

2D structure of the optimised endo dimer 2

In 3D :

Optimised structure of cyclopentadiene exo dimer

Optimised structure of cyclopentadiene endo dimer

Breakdown of the energy contributions of the exo dimer 1
Total bond stretching energy	3.55028 kcal/mol
Total angle bending energy	30.78911 kcal/mol
Total stretch bending energy	-2.04253 kcal/mol
Total torsional energy	-2.73409 kcal/mol
Total out-of-plane bending energy	0.01012 kcal/mol
Total van der Waals' energy	12.79132 kcal/mol
Total electrostatic energy	13.01103 kcal/mol
TOTAL ENERGY	55.37525 kcal/mol

Breakdown of the energy contributions of the endo dimer 2
Total bond stretching energy	3.46169 kcal/mol
Total angle bending energy	33.29189 kcal/mol
Total stretch bending energy	-2.08130 kcal/mol
Total torsional energy	-2.96391 kcal/mol
Total out-of-plane bending energy	0.01571 kcal/mol
Total van der Waals' energy	12.28769 kcal/mol
Total electrostatic energy	14.18087 kcal/mol
TOTAL ENERGY	58.19264 kcal/mol

The dimerisation process of the cyclopentadiene to form dicyclopentadiene is a pericyclic [4+2] Diels-Alder cycloaddition reaction and it produces the endo dimer 2 specifically. This can be rationalised by studying the energies of the exo and endo dimers 1 and 2 above. It is found that the endo dimer 2 is less thermodynamically stable than its exo counterpart, i.e. it has a higher overall ground state energy of 58 kcal/mol (relative to the exo energy of 55 kcal/mol). Therefore, it is expected that the exo product would be formed preferentially as it has a lower energy and is more thermodynamically stable. However, the endo dimer 2 is found to be the predominant product.

Why is this so? This is can be understood by analysing the transition state for the cycloaddition of the two cyclopentadiene rings as kinetically-controlled reactions can be understood by their stabilities of their transition states. The cycloaddition process can occur thermally or photochemically but it is not specified which one is occuring in the above example and therefore we are unable to conclude whether the reaction occurs suprafacially or with antarafacial components. As a cycloaddition reaction is a pericyclic reaction, it has only one transition state and as the cyclopentadiene molecule is planar, there are two possible sites of attack of the dienophile, from the top face or from the bottom face of the diene.

Possible mode of attack for the transition state of the cycloaddition reaction

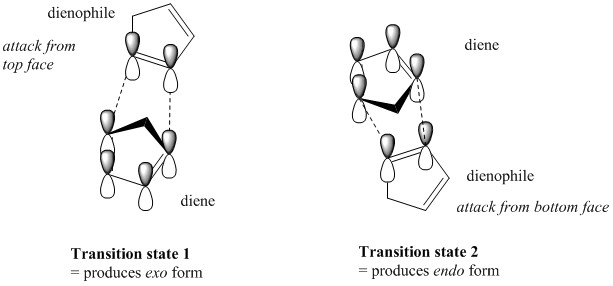
The kinetic endo product 2 has a lower activation energy by virtue of favourable orbital overlap of the p-orbitals in the transition state that stabilities the kinetic endo dimer 2, causing it to be formed faster at room temperature, although the thermodynamic exo product 1 is more stable. The thermodynamic exo dimer 1 is more stable due to less steric hindrance of nearby hydrogens relative to the endo form.

The dimerisation of cyclopentadiene is therefore a kinetically controlled process and forms the kinetic endo product 2 preferentially.

Hydrogenation of the endo dimer 2

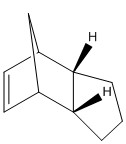
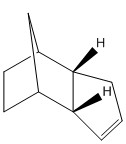
Hydrogenation of each of the double bonds of the endo dimer 2 occurs preferentially to produce two different dihydro derivatives 3 and 4 below. Prolonged hydrogenation produces the tetrahydro derivative, but this shall not be considered in our models below.

Dihydro derivative 3 and 4 of the endo dimer 2

Dihydro derviative 3 of the endo dimer 2

Dihydro derivative 4 of the endo dimer 2

2D structure of the optimised geometry of the dihydro derivative 3

2D structure of the optimised geometry of the dihydro derivative 4

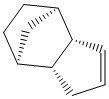
In 3D : Optimised structure of cyclopentadiene dihydro dimer derivative 3

Optimised structure of cyclopentadiene dihydro dimer derivative 4

Breakdown of the energy contributions of the dihydro derivative 3
Total bond stretching energy	3.35211 kcal/mol
Total angle bending energy	29.01451 kcal/mol
Total stretch bending energy	-2.08251 kcal/mol
Total torsional energy	-0.22007 kcal/mol
Total out-of-plane bending energy	0.01262 kcal/mol
Total van der Waals' energy	13.48930 kcal/mol
Total electrostatic energy	5.11303 kcal/mol
TOTAL ENERGY	48.67900 kcal/mol

Breakdown of the energy contributions of the dihydro derivative 4
Total bond stretching energy	2.93280 kcal/mol
Total angle bending energy	21.11026 kcal/mol
Total stretch bending energy	-1.71130 kcal/mol
Total torsional energy	0.20617 kcal/mol
Total out-of-plane bending energy	0.00064 kcal/mol
Total van der Waals' energy	10.64281 kcal/mol
Total electrostatic energy	5.14871 kcal/mol
TOTAL ENERGY	38.33009 kcal/mol

The two products of hydrogenating one C=C double bond in the kinetic dimer 2 are 3 and 4. Analysis of their inherent energies shows that the dihydro derivative 4 is more thermodynamically stable than the dihydro derivative 3, as almost all its energy contributions from stretching, bending and van der Waals' interactions are lower than 3 and this results in molecule 4 having a lower energy than that of molecule 3. This suggests that the hydrogenation of the C=C double bond in the norbornene ring is thermodynamically more favourable than hydrogenating the C=C double bond in the pentane ring as it produces a product with a lower energy. This is supported by the heat of hydrogenations of the double bonds. Hydrogenation reactions are always exothermic and the numerical values of the heat of hydrogenations are indicative of the stability of the C=C double bond. The smaller the value of the heats of hydrogenation, the more stable the C=C double bond. The heats of hydrogenation of norbornene is -33.83 kcal/mol and cyclopentene is -26.6 kcal/mol. Therefore, the C=C double bond in norbornene is less stable and hence more reactive towards hydrogenation compared to cyclopentene.

Therefore, the hydrogenation of the endo dimer 2 to give the dihydro derivative with the pentane ring 3 is kinetically favoured and the dihydro derivative 4 formed from hydrogenating the C=C bond in the heptane ring is thermodynamically favoured.

Atropisomerism in an Intermediate related to the Synthesis of Taxol

Taxol, a synthetic drug used in the treatment of cancer, is a macrocyclic compound made from different monomer units. One of the key intermediates in the total synthesis of taxol are 9 or 10 below.

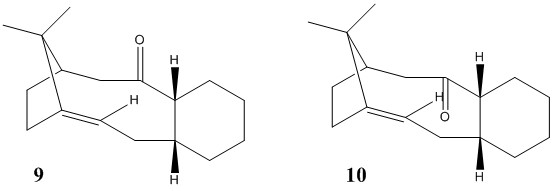
The two intermediates are isomers of each other and the most stable isomer determined by using the MMF494 force field in the ChemBio3D program. These isomers exhibit a special type of isomerism called atropisomerism, which arises from a highly strained structure, which lead to hindered rotation around single bonds and therefore, renders the steric strain energy barrier to rotation sufficiently high that permits isolation of the two isomers.

The carbonyl group on the bicyclic compound can be pointing upwards or downwards and this leads to different 3D configurations of the isomers and hence, different stabilities and reactivities. In order to predict, which is the more stable isomer, the two isomers are modelled using the MMF494 force field and their geometries optimised to calculate and compare which isomer has a lower ground state energy.

In order to simplify the results, we shall assume that no ring-flipping of the cyclohexane ring occurs and that the two hydrogens attached to the carbons on the cyclohexane ring fused to on the norbornene-like ring will only adopt a cis conformation. It should, however, be noted that although the norbornene-like ring is conformationally fixed, the cyclohexane ring is not and different conformers should produce different ground state energies of the isomers 9 and 10 and these isomers can be isolated due to atropisomerism.

Energies of the two isomers
Isomer	Energy (kcal/mol)	Conformation of the cyclohexane	3D structure of the isomer
Isomer 9	70.5493	Chair	Isomer 9 chair conformation ‎
Isomer 9	76.30330	Twist-boat	Isomer 9 twist-boat conformation
Isomer 10	60.55901	Chair	Isomer 10 chair conformation
Isomer 10	77.852	Twist-boat	Isomer 10 twist-boat conformation

The cyclohexane ring exists in four main conformations that are chair, half-chair, twist-boat and boat. These conformers readily interconvert between one another due to the low energy barrier to rotation. However, when the cyclohexane ring is combined with the norbornene-like ring, the rotation around single bonds become hindered and the half-chair structure is too high in energy and hence is not considered. Analysis of the energies of the cyclohexane conformers show that the chair conformation of cyclohexane does indeed produce the lowest energy conformer and is the most likely conformation adopted by the isomers 9 and 10. Isomer 10, which has its carbonyl facing downwards, has a lower energy (60.55901 kcal/mol) than the corresponding isomer 9 (70.5493 kcal/mol) when it is in it chair conformations. It is therefore more stable than isomer 9 when they are in their lowest energy conformation (chair). The energies of the chair conformation are shown to be lower than the corresponding twist-boat structures. It is interesting to note, however, that the energies of the two isomers in their twist-boat structures are quite similar and that the energy of the twist-boat conformer of isomer 10 is actually higher than that of isomer 9 (77.852 and 76.30330 kcal/mol). This suggests that in the twist-boat conformer, the two isomers adopt structures that are most similar to each other.

Isomer 10, which has its carbonyl group facing downwards, is thermodynamically more stable (60.55901 kcal/mol) than isomer 9 (70.5493 kcal/mol) in its chair conformation and is the more stable isomer. This is due to less steric repulsion between the carbonyl group and the methyl groups on the bridging carbon. This hypothesis can be backed up by the energy of the isomer when there are no methyl groups attached to the bridging carbon. It is calculated that isomer 10 (the more stable isomer) has an energy of around 43 kcal/mol when there are no methyl groups attached to the bridging carbon. Comparing this value to when the two methyl groups are present (60.55901 kcal/mol), this suggests that the steric repulsions caused by the presence of the methyl groups causes quite a significant effect on the overall energy of the isomer. The steric repulsions of the methyl groups with the higher energy conformations of the cyclohexane ring causes a significant contribution to the increase in energy of the isomers. Modifying the substituents to smaller sizes (e.g. hydrogens) on the bridging carbon should be able to minimise the energy of the molecule further.

Since isomer 10, with its downward facing carbonyl group, has been found to be the more stable isomer, it is now possible to determine with relative accuracy, the stereochemistry with which carbonyl addition occurs. The predominant diastereoisomer formed from nucleophilic attack on the carbonyl can be predicted using the Felkin-Anh model. This model works only if the subtrate does not contain an alpha-heteroatom that has lone pairs that are available for coordination and if the reagent or catalyst does not contain a metal ion that can coordinate to more than one heteroatom at once, which would lead to chelation control and produce the opposite result to that predicted by the Felkin-Anh model.

The alkene C=C bond in the isomers are expected to be relatively reactive towards functionalisation. However, this is not the case and functionalisation of these alkenes are abnormally slow. This decreased reactivity due to their location as bridgehead olefins. These type of alkenes are called hyperstable olefins and they are less strained than their parent hydrocarbons, resulting in decreased reactivity towards functionalisation.

The strain energy of the bridgehead olefins is made up of the additional strain caused by the double bond and the residual strain of the carbon skeleton. The additional strain of the double bond is called olefinic strain (OS) and is indicative of the stability of bridgehead olefins. Bridgehead olefins contained in a large carbon ring such as isomers 9 and 10 above must have a trans-conformation and have a negative OS value, meaning that the C=C double bond is less strained than its corresponding C-C single bond. The lower the value of the OS, the more stable is the double bond. This is due to the special stability provided by the cage structure of the carbon backbone and the greater strain of the parent alkane.

Spectroscopic Simulation using Quantum Mechanics

The isomers 9 and 10 above are but one of the many precursors in the total synthesis of Taxol. Derivatives of these isomers have been synthesised are two examples are molecules 17 and 18 below.

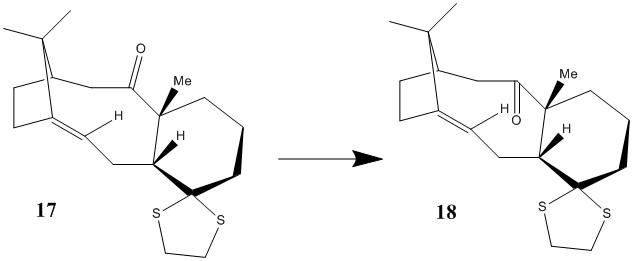
Structure 17 can be converted into structure 18 thermally by prolonged heating in THF solvent.

The structures of both isomers 17 and 18 were modelled using the MMF494 force field and their geomtries optimised to calculate their minimum energy conformations. This was then used to study their relative stabilities.

Energies of the Taxol Intermediates 17 and 18
	Minimum energy conformation (kcal/mol)	Gibbs free energy ΔG (kcal/mol)	Gibbs free energy ΔG (kJ/mol)
Taxol intermediate 17	106.27206	-1036303.994564	-4335895.913258
Taxol Intermediate 18	100.50952	-1036309.650936	-4335919.579516

The two free energies of isomers 17 and 18 have a difference of about 25 kJ/mol with isomer 18 having a lower free energy than 17. This corresponds to the fact that isomer 18 has a lower minimum energy as calculated by the MMF494 force field. Since the free energy is directly related to the K_eq (all else being equal), we can make the conclusion that the formation isomer 18 would be greatly favoured compared to the isomer remaining in the configuration of isomer 17.

The ¹H and ¹³C NMR spectra were modelled quantum mechanically using Gaussian and the HPC system and compared to the chemical shifts reported in the literature^[9] by L. Paquette, N. A. Pegg, D. Toops, G. D. Maynard, R. D. Rogers to see if there are any differences between the chemical shifts reported by the literature and the one predicted by the Gaussian and HPX system.

It is important to take note that the two quantum mechanical NMRs modelled were run in deuterated chloroform, rather than deuterated benzene as specified in the literature. So we would expect some derivations in the chemical shifts due to the use of different solvents ("the solvent effect"). The ¹H NMR shift for benzene-d and chloroform-d are 7.16 and 7.24ppm respectively, a very small difference so we would expect the chemical shifts of the two NMR spectrums to be relatively similar. For the ¹³C NMR, however, the chemical shifts of benzene-d and chloroform-d is markedly different (128.4 and 77.23ppm) and the solvent effect is expectedly to be significantly greater in ¹³C NMR than ¹H NMR. Therefore, part of the difference in the chemical shifts between that reported in the literature and the calculated NMR spectrum would be due to the solvent effect and the magnitude of the solvent effect is expected to be greater in the ¹³C NMR than the ¹H NMR spectrum.

The tables below outline the differences between the chemical shifts recorded by our quantum mechanical calculations and the chemical shifts reported by Paquette.

1H NMR chemical shifts for Taxol intermediate 18
Chemical shifts/ppm
Literature values	Predicted values
5.21	5.99
3.00-2.70	3.14
	3.14
	3.00
	2.93
	2.93
	2.81
2.70-2.35	2.81
	2.61
	2.56
	2.48
2.20-1.70	2.34
	2.34
	2.28
	2.00
	2.00
	1.85
1.58	1.85
1.50-1.20	1.65
	1.58
	1.52
1.10	1.52
	1.36
	1.31
1.07	1.22
	1.22
	0.95
1.03	0.95
	0.95
	0.62

¹H NMR spectrum of Taxol intermediate 18

The ¹H NMR spectra show differences between the simulated and literature chemical shifts of up o 0.7ppm. Due to the narrow chemical shift range of ¹H NMR, even a 0.1ppm difference is quite a significant difference and could lead to the shift appearing in a region that has little correlation with its actual chemical environment. As intermediate 18 is a relatively large molecule containing a lot of hydrogens in similar chemical environments, it is only really possible to assign hydrogens adjacent or directly attached to functional groups.

The assignments of the chemical shifts are as follows; 5.21ppm olefinic proton, 3.00-2.70ppm hydrogens adjacent to the C=O group, 2.70-2.35ppm hydrogens on carbon adjacent to the sulphur atoms, 2.20-1.70ppm hydrogens on the two methyl substituents on the bridgehead carbon, 1.58ppm hydrogen of the bridgehead carbon. The rest of the chemical shifts correlate to the hydrogens attached to rest of the alkane carbons.

The difference between the simulated and literature chemical shifts of the ¹H NMR spectra is caused by advancement in NMR techniques over the years that has led to more accurate NMR measurements. Computational modelling was used to simulate the NMR spectrum and this technique is still relatively new and therefore, the programs used to simulate the NMR spectrum may not be as advanced as it can be. Combining these two factors would lead to definite discrepancies between simulated and actual NMR chemical shifts.

13C NMR chemical shifts for Taxol intermediate 18
Chemical shifts/ppm
Literature values	Predicted values	Difference
211.49	213.05	1.56
148.72	148.00	-0.72
120.90	120.22	-0.68
74.61	93.27	18.66*
60.53	65.94	5.41*
57.30	55.03	-2.27
50.94	55.03	4.09*
45.53	49.68	4.15*
43.28	48.12	4.84*
40.82	45.80	4.98*
38.73	44.16	5.43*
36.78	41.35	4.57*
35.47	38.73	3.26
30.84	33.72	2.88
30.00	32.58	2.58
25.56	28.41	2.85
25.35	26.51	1.16
22.21	24.57	2.36
21.39	24.17	2.78
19.83	22.59	2.76

¹³C NMR spectrum of Taxol intermediate 18

The chemical shifts of the ¹³C NMR spectrum calculated by quantum mechanical calculations show a general similarity to that reported by Paquette (within a 0.5-3ppm difference). ¹³C NMR has a much wider chemical shift range than that of ¹H NMR and therefore chemical shifts differences of a few ppm is not such a significant effect as in ¹H NMR. The values marked with an * highlight the particular chemical shifts that show a marked difference between the literature and the predicted values. This difference can be accounted for by the heavy atom effect caused by the presence of the two sulphur atoms in the intermediate 18. This effect is most significant in carbons alpha to the sulphur atoms and its effect runs opposite to electronegativity. This effect causes a shift to lower frequency, and a corresponding increase in chemical shift. There therefore needs to be a spin-orbit coupling correction for the heavy atom effect caused by the presence of sulphur in order to increase the accuracy of the chemical shift values of the NMR spectrum. It is difficult to assign with accuracy most of the chemical shifts in the simulated spectrum due to the similarity of the chemical shift values and comparison with the literature is difficult due to lack of assignments of the shifts in the literature and the fact that the differing values between the simulated and literature chemical shifts sometimes result in overlapping values of chemical shifts.

Overall, the simulated ¹³C NMR spectrum shows more correlation to the literature than the simulated ¹H NMR spectrum. This suggests that the Gaussian and HPC computational program is more accurate in modelling ¹³C spectra compared to ¹H spectra. Although there are discrepancies between the actual and simulated spectras, computational modelling is a useful technique for being able to predict NMR spectras of different compounds and as a reference to compare with an actual spectrum.

Analysis of the Properties of trans-stilbene and styrene epoxides

The asymmetric epoxidation of alkenes is a very versatile process and can be used to form epoxide products that are highly reactive due to its strained ring structure. Epoxides can therefore be useful as precursors to a range of other functionalities. Catalysts can be used in epoxidation reactions and below, the crystal structures of two asymmetric catalysts, namely the Shi catalyst (an organic molecule) and the Jacobsen catalyst (a transition metal complex) was analysed using the ConQuest and Mercury computer programs.

Shi Catalyst

The Shi catalyst has a structure is a derivative of a pyranose sugar ring and is an organic catalyst. The crystal structure stable precursor of the Shi catalyst was drawn on ConQuest and exported to Mercury for an analysis of the bond lengths of the anomeric carbons. The pyranose ring contains an anomeric carbons which can exhibit the anomeric effect, a stereoelectronic effect that results in an anomalous preference of a heteroatom substituent adjacent to a heteroatom in a cyclohexane ring to adopt the axial orientation rather than the less-hindered equatorial orientation.

There are two anomeric carbons (i.e. those having O-C-O substructures) in the precursor to the Shi catalyst, molecule 21 namely O₂-C₇-O₁ and 0₅-C₁₀-O₄. A typical C-O bond length is around 1.43Å but it is seen that the each of the anomeric carbons has one C-O bond that is slightly longer (O₂-C₇ 1.441Å, O₄-C₁₀1.439Å) and one that is slightly shorter than this length (0₁-C₇ 1.413Å, 0₅-C₁₀ 1.409Å). This is due to the anomeric effect. Although the reason for the anomeric effect has not been fully understood, a widely accepted explanation is that the lone pair on the oxygen (on O₁ and O₅ respectively) can donate into the anti-bonding σ* orbital on the adjacent C-O bond. The donation of the oxygen lone pair causes a weakening of the anti-bonding σ* C-O bond, leading to a reduction in bond order and an elongation of the C-O bond. This is a stabilising interaction (termed "hyperconjugation") that results in an alignment of the oxygen lone pair donor antiperiplanar to the σ* C-O bond, lowering the total energy of the system and increased stability of the axial conformation.

All the other non-anomeric C-O bonds have a bond length of about 1.40-1.41Å, slightly shorter than typical C-O bond lengths, due to them being constrained into a 5-membered ring.

Jacobsen Catalyst

The crystal structure of the Jacobsen catalyst 23 was modelled using ConQuest and its properties observed on Mercury.

Jacobsen catalyst 3D structure

The manganese metal centre is expected to the reactive site that binds to the alkenes during the epoxidation due to its ability to change its oxidation state. Upon analysis of the crystal structure of Jacobsen catalyst, we can deduce that there are actually 3 possible sites of attack by the alkene.

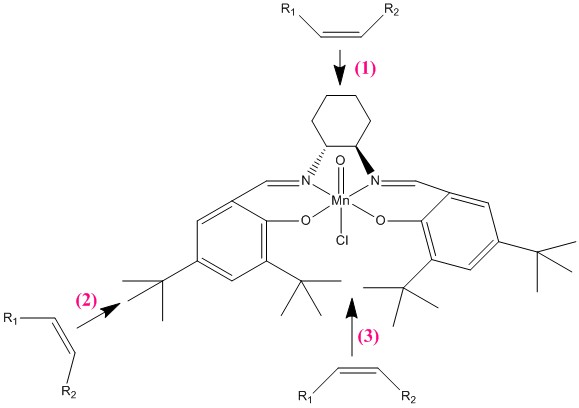
In the Jacobsen catalyst, the Mn centre is sterically protected by the three bulky benzenoid rings surrounding the metal centre. The tert-butyl groups on the benzene rings provide additional protection by increasing the steric bulk of the molecule and prevents the alkene from approaching the metal centre from the both sides, disfavouring method 2 of attack.

The alkene could also attack from below (method 3) but again, the benzenoid ring and the tert-butyl groups sterically shield the metal centre from attack.

Therefore, method 1, attack by the top face is the most favoured method of attack of the alkene to the metal centre as there is least steric hindrance from the cyclohexane ring. The Jacobsen catalyst selectively epoxides cis-alkenes in the presence of trans alkenes because the trans alkenes would have one substituent pointing in the direction of the metal centre and this causes steric clash with the cyclohexane ring when the alkene approaches the metal centre from the top face.

Trans-stilbene

The trans-stilbene epoxide was modelled using ChemBio3D to calculate which the ground state energies of the product. There are 4 possible diastereomers of the trans-stilbene epoxide that can be formed.

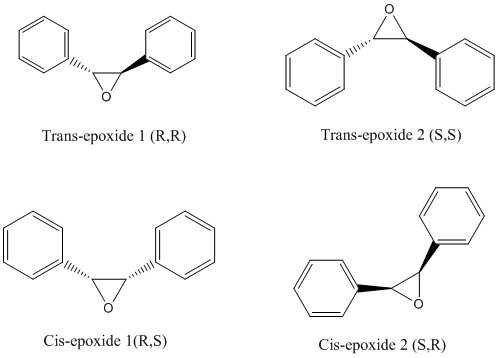
Their energies are listed below :

Trans-epoxide 1 (R,R)	39.6882 kcal/mol
Trans-epoxide 2 (S,S)	39.4867 kcal/mol
Cis-epoxide 1 (R,S)	41.7314 kcal/mol
Cis-epoxide 2 (S,R)	41.7975 kcal/mol

The two cis-epoxides have a higher ground state energy than the trans-epoxides and are unlikely to be formed during the epoxidation reaction as trans-stilbene has an initial trans configuration and the reaction for the Jacobsen epoxidation was carried out at room temperature and the Shi epoxidation was carried out at 0 degrees Celsius in the lab. There is no extra energy inputted into the epoxidation reaction by heating and hence, the molecule cannot change its configuration from trans to cis during the epoxidation. Thus, for the epoxidation reactions with Jacobsen and Shi, the two possible diastereomers formed is either (R,R) or (S,S) trans-epoxides.

The 1H and 13C NMR for the these (R,R) and (S,S) epoxides were modellled in chloroform solvent and are shown below.

(R,R) trans-stilbene epoxide :

¹H NMR spectrum

¹³C NMR spectrum

(S,S) trans-stilbene epoxide :

¹H NMR spectrum

¹³C NMR spectrum

From the calculation of the minimum energy of the enantiomers using the MMFF94, the program predicted the (S,S) trans-epoxide 2 to have a slightly lower energy than its (R,R) counterpart, i.e. (S,S) epoxide is generally more thermodynamically stable than (R,R).

Analysis of the energies transition states of each enantiomer would give further detail on which stereoisomer would be predominantly formed during the epoxidation reactions with the two asymmetric catalysts, Shi and Jacobsen respectively.

(i) Epoxidation using the Shi catalyst :

Gibbs free energies ΔG, of the transition states of the (R,R) and (S,S) trans-stilbene epoxides (Hartree/Principle)
(R,R)	(S,S)
-1534.687808	-1534.683440
-1534.687252	-1534.685089
-1534.700037	-1534.693818
-1534.699901	-1534.691858

The 8 possible transition states for the (R,R) and (S,S) configurations of the trans-stilbene epoxide each gives rise to different free energies, ΔG. The transition state of (R,R) on the third row has the lowest ΔG and is the most energetically accesible transition state. Therefore the trans-stilbene alkene would be predicted to react fastest via this transition state during the Shi epoxidation to form the epoxide with an absolute configuration of (R,R), which is the kinetic product of the reaction.

The enantiomeric excess of the Shi epoxidation can be calculated from the equation ΔG = -RT ln K_eq. The lowest energy transition states of (R,R) and (S,S) diastereomers are the ones located on the third row of the table above and the difference between them is 16.3279857 kJ/mol. Substituting this value into the equation, the value for K_eq is found to be approximately 0.00137.

The enantiomeric excess (e.e.) of the reaction is found by the equation :

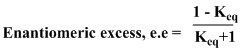
For the Shi epoxidation, the e.e. calculated is 99.7% in favour of the (S,S) absolute configuration of the trans-stilbene epoxide. The literature calculates the e.e. for the Shi epoxidation of trans-stilbene to be 98.3% with an absolute configuration of (S,S) so this corresponds quite well with the calculations we conducted.

(ii) Epoxidation using the Jacobsen catalyst :

Gibbs free energies ΔG, of the transition states of the (R,R) and (S,S) trans-stilbene epoxides (Hartree/Principle)
(R,R)	(S,S)
-3574.923087	-3574.921174

Each configuration has only one possible transition state due to the bulky protecting groups around the metal centre of the Jacobsen catalyst as mentioned above, allowing only one mode of attack of the alkene. The (R,R) epoxide has a lower ΔG and this is therefore the (R,R) epoxide is predicted to form predominantly via this lowest energy transition state due to kinetic reasons.

The enantiomeric excess of the Jacobsen epoxidation can be calculated from the equation ΔG = -RT lnK_eq, as before. The difference between the two transition states of the diastereomers is 5.02258188 kJ/mol. Substituting this value into the equation, the value for K_eq is found to be approximately 0.132.

The calculated e.e. value for the Jacobsen epoxidation of the trans-stilbene was calculated to be 76.7% in favour of the absolute (S,S) configuration of the resulting epoxide. This is a quite a significant differene from the value of the e.e. reported in the literature of 33% for (S,S) configuration.

Styrene

Styrene is a terminal monosubstituted alkene and therefore is expected to have 2 possible isomers upon epoxidation as it has only one chiral centre. As before, the two possible epoxide enantiomers were modelled using the MMFF94 force field in ChemBio3D to predict the minimum energies of the two enantiomers.

The 1H and 13C NMR for the these R and S enantiomers were modelled using HPC and GaussView in chloroform solvent and are shown below.

(R)-styrene oxide :

¹H NMR spectrum

¹³C NMR spectrum

(S)-styrene oxide :

¹H NMR spectrum

¹³C NMR spectrum

The minimum energies of the enantiomers are listed below:

R enantiomer	21.6586 kcal/mol
S enantiomer	21.6336 kcal/mol

The two enantiomers have very similar ground state energies but the S enantiomer has a slightly lower energy, suggesting it to be the thermodynamic product of the reaction. Further analysis of their transition state energies is required to determine whether or not the thermodynamically more stable S enantiomer would indeed be formed during the course of the reaction.

(i) Epoxidation using the Shi catalyst :

Each enantiomer of the epoxide has four possible transition states and therefore the energies of these 8 possible transition states were simulated and predicted. These energies are reported below :

Gibbs free energies ΔG, of the transition states of the R and S styrene epoxides enantiomers (Hartree/Principle)
R enantiomer	S enantiomer
-1303.730703	-1303.733828
-1303.730238	-1303.724178
-1303.736813	-1303.727673
-1303.738044	-1303.738503

The lowest activation energy transition states (i.e. ΔG) for the R and S enantiomers are the ones on the last row of the above table, with the S enantiomer having a slightly lower activation energy to access its lowest energy transition state. The S enantiomer is therefore predicted to be formed the fastest via this transition state and is the kinetic product of the reaction.

The difference in their lowest energies ΔG, is calculated to be 12.051046 kJ/mol and the corresponding Keq is calculated to be 0.00772. The enantiomeric excess calculated is 98.5% in favour of the R enantiomer, and this correponds to the absolute configuration of the R epoxide formed in the literature although the e.e. calculated in the literature is 24.3%, much lower than our calculated e.e. value.

(ii) Epoxidation using the Jacobsen catalyst :

Each enantiomer of the epoxide product has 2 possible transition states and the minimum energies to access each transition state (ΔG) is listed below.

Gibbs free energies ΔG, of the transition states of the R and S styrene epoxides enantiomers (Hartree/Principle)
R enantiomer	S enantiomer
-3343.960889	-3343.969197
-3343.962162	-3343.963191

The S enantiomer is again observed to have the lowest ΔG to access the lowest energy transition state and the difference between the lowest ΔG of both enantiomers is 18.4703939 kJ/mol. The corresponding K^eq for this is 0.000579.

The enantiomeric excess calculated from the K_eq above gives a value of 99.9% of the R enantiomer product but the literature reports an e.e. value 57% for the R enantiomer.

For both alkenes, it is observed that the epoxidation reaction using the Jacobsen catalyst leads to a lower activation energy to the transition states i.e. lower ΔG compared to the Shi catalyst and this means that in general, less energy is required to epoxide the alkenes using the Jacobsen catalyst. This is the reason why the reaction conditions for the Jacobsen epoxidation is simply at room temperature with stirring only. No additional energy input is required for this reaction to occur.

The calculated e.e. values seems to vary quite significantly from that reported in the literatures and this suggests that perhaps there is a deficiency in the simulation of the transition states and their energies and that a correction factor may need to be included in the calculations to get an accurate representation of the predicted e.e. values.

Assignment of the absolute configuration of the epoxide products using simulated optical rotation values

The analysis done on the transition states of each disastereomer of each epoxide product has allowed us to deduce that for the trans-stilbene epoxide, the (S,S) configuration is the one predominantly formed using both the Shi and Jacobsen catalyst. For styrene-oxide, the enantiomer predominantly formed would be the (R)-epoxide. The optical rotations of these configurations of the stilbene and styrene epoxide were then simulated using quantum mechanics and compared to literature in order to further consolidate the absolute configuration of the predominant epoxide formed is indeed what we have deduced it to be earlier. The simulated optical rotations were carried out in chloroform solvent.

Optical rotation values
Epoxide and its configuration	Literature value	Simulated value
(S,S)-trans-stilbene oxide	-334.3	-351.8
(R)-styrene oxide	-21.1	-32.5

The simulated values vary greatly with the literature because the optical rotations were done in different solvents (ethanol for trans-stilbene, styrene oxide was measured in chloroform). The solvent effect leads to a deviation of the value from that measured in chloroform. Also, the method of synthesis used in the two literature journals are different from the Shi and Jacobsen epoxidation methods we used to synthesise these epoxides in the lab. The differing reaction conditions and starting materials used in these could be a cause for the difference in values.

There are other types of chiroptical computational analysis could be done on the epoxide such as calculating the electronic circular dichroism (ECD) and the vibrational circular dichroism (VCD) properties of the epoxides but we did not simulate these properties as the ECD would not be able to tell us anymore useful information about our epoxide products and there is very little literature references to which we can compare the simulated VCD values to. So measuring the optical rotation of our epoxide remains the most useful method that aids in the identification of the absolute configuration of the epoxide product formed.

Investigating the non-covalent interactions in the active-site of the reaction transition state

In order to understand the mechanism of formation of the epoxidation, we shall apply NCl analysis on the lowest energy transition state of the (S,S) trans-stilbene with the Shi catalyst. NCl analysis allows us to investigate the non-covalent interactions present in the transition state. The difference colours in the transition state are indicative of these non-covalent interactions with blue and green corresponding to attractive interactions and red and yellow to repulsive interactions.

There are two possible transition states that the epoxidation can undergo, spiro or planar. Observation of this model shows a largely attractive transition state, implying that the epoxidation of trans-stilbene occurs via a spiro transition state, which is stabilised by these attractive non-covalent forces. This spiro transition state is favoured over the planar transition state because it allows the anti-bonding π^* C=C orbital of the alkene to overlap with the lone pair of electrons on the oxygen atom, stabilising the transition state by reducing the energy of the system. This overlap cannot occur if the epoxidation occurs via the planar transition state.

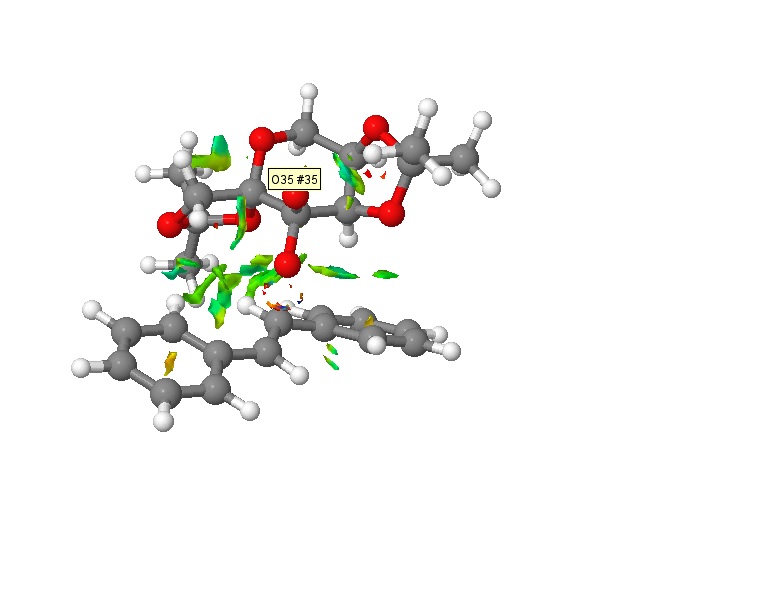
Attractive forces are also observed between oxygen and hydrogen atoms in this transition, implying hydrogen bonding which also aids in stabilising the transition state. Some mildly repulsive forces exist within the aromatic benzene rings due to the delocalised cloud of π electrons but this is expected of aromatic rings and these forces are small compared to the attractive forces present and this leads to an overall stabilisation of the transition state.

Investigating the electronic topology (QTAIM) in the active-site of the reaction transition state

We have already studied the non-covalent bonds present in the transition state in the NCl analysis above and now we turn our attention to the covalent bonds present in the molecule and how their bonding contributes to the overall energy of the transition state.

The lowest energy transition state of the (S,S) trans-stilbene epoxide formed using the Shi catalyst was modelled using Avogadro and subjected to QTAIM analysis to study the electron densities of the bonds in the molecules. The QTAIM diagram allows us to study and understand chemical bonding and structure of a molecule by identifying topological points called bond critical points (BCPs), which is defined by a region where the first derivative of the electron density with respect to each of the 3 coordinates of that point is equal to zero. This region has a curvature which is mathematically defined by the Hessian of the density p(r) appropriate for a bond.

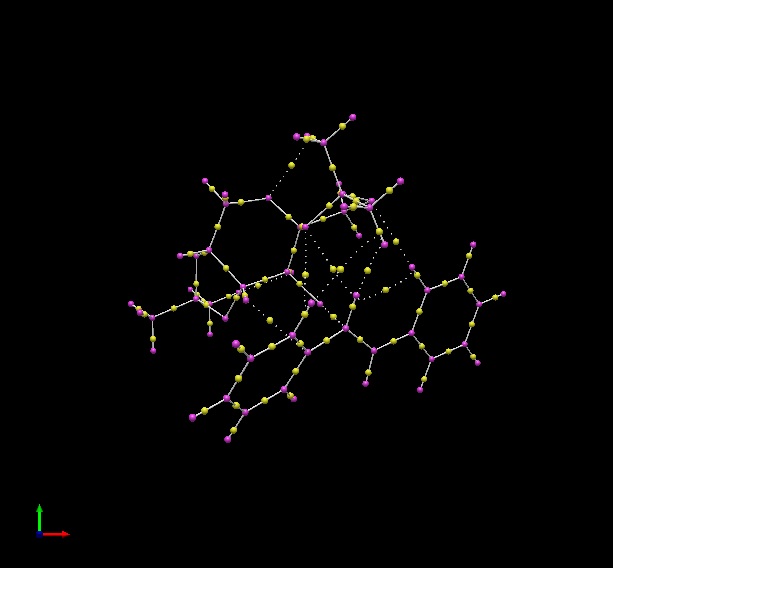
The yellow points represent BCPs in the transition state. There are two main types of BCPs observed, i.e. covalent BCPs and weakly bonded, non-covalent BCPs. The covalent BCPs are those yellow points connecting two purple points (actual atoms) by a straight black line. The weakly bonded BCPs connect two purple points which represent actual atoms by a dashed line.

Covalent BCPs are indicative of the strength and polarity of a covalent bond between two atoms. For two homonuclear atoms, the BCP would be expected to be located at its ideal location midway between the two nuclei, as seen in C-C bonds in benzene in this transition state, i.e. electron density is shared equally between the two homonuclear atoms. For two heteroatoms having different polarities e.g. the C-O bonds in the transition state of the Shi epoxidation of (S,S) trans-stilbene epoxide, the electron density would be more polarised towards O, the more electronegative atom. This results in the BCP being located nearer to more electronegative oxygen atom. The greater the difference in electronegativity between these two heteroatoms, the bigger the deviation of the BCP from its ideal location midway between the distance between the two nuclei.

Weakly-bonded, non-covalent BCPs refer to, in this example, the hydrogen bonding that occurs between the O and H heteroatoms that help stabilise and reduce the energy of this transition state. Each oxygen atom is noted to be form two of such type of interactions do two hydrogen atoms by virtue of it having two lone pairs. It is interesting to note that in the active site for this transition state, the BCPs form weak, non-covalent bonds to each other and it is most probable that it is these interactions that help to stabilise the formation of the epoxide product. These can also be observed in the NCl analysis conducted on the transition state earlier and therefore, this data consolidates the observation made earlier regarding fairly extensive hydrogen bonding helping to stabilise the transition state of the Shi epoxidation of the trans-stilbene to favour the formation of the (S,S)-trans-stilbene oxide product.

Suggesting new candidates for investigations

It is worthwhile studying the effect of larger alkene rings on their epoxidation reactions. One such example is cyclooctene. As the ring size increases, the number of conformers it has increases as well. The lack of chiral centres means that we will not need to consider the formation of diastereomers, and can focus solely on the mechanism epoxide formation. It might be possible to observe a trend in which the major epoxide formed can be predicted from the ring size and the effect of different substituents and their location relative to the ring.