Rep:Mod:cjmodule3
Module 3
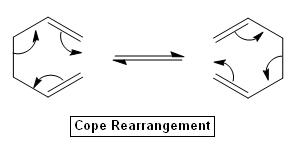
The Cope Rearrangement
There are 6 pi-electrons involved in the cope rearrangement and it follows the 4n+2 Hückel's aromaticity rule.
The reaction concerned in this exercise is the rearrangement of 1,5-hexadiene, to study this rearrangment, the conformational isomers of the starting material are firstly analysed by calculating the low-energy minima and transition state structures using GaussView.
Anti and Gauche Conformer of 1,5-hexadiene
The starting material, 1,5-hexadiene, has three C-C single bonds and they can all rotate freely. Effectively, this feature allows the 1,5-hexadiene has 27 possible conformers, However, due to the relationship between symmetry and enantiomeric effect, only 10 conformers out of 27 are energetically distinct.
The structures of 10 conformers are optimised by GaussView in different calculation methods and compared blow:
| Conformer | gauche-1 | gauche-2 | gauche-3 | gauche-4 | gauche-5 | gauche-6 | anti-1 | anti-2 | anti-3 | anti-4 |
|---|---|---|---|---|---|---|---|---|---|---|
| Structrue of Conformer | ||||||||||
| Point Group | C2 | C2 | C1 | C2 | C1 | C1 | C2 | Ci | C2h | C1 |
| Optimised Energy -HF/3-21G [hartree] | -231.68772 | -231.69167 | -231.69266 | -231.69153 | -231.68962 | -231.68916 | -231.69260 | -231.69254 | -231.68908 | -231.69097 |
| Relative Energy -HF/3-21G [kcal/mol] | 3.1 | 0.62 | 0.00 | 0.71 | 1.91 | 2.20 | 0.04 | 0.075 | 2.25 | 1.06 |
| Optimised Energy -DFT/6-31G(d) [hartree] | -234.60788 | -234.61069 | -234.61133 | -234.61049 | -234.60911 | -234.60889 | -234.61179 | -234.61172 | -234.60962 | -234.61079 |
| Sum of electronic and zero-point Energies [hartree] | -234.465220 | -234.468261 | -234.468693 | -234.467784 | -234.466368 | -234.466281 | -234.469298 | -234.469176 | -234.467017 | -234.468193 |
| Sum of electronic and thermal Energies [hartree] | -234.458101 | -234.460957 | -234.461463 | -234.460521 | -234.459214 | -234.459104 | -234.461967 | -234.461834 | -234.459822 | -234.460942 |
| Sum of electronic and thermal Enthalpies [hartree] | -234.457157 | -234.460013 | -234.460519 | -234.459577 | -234.458269 | -234.458160 | -234.461022 | -234.460890 | -234.458878 | -234.459998 |
| Sum of electronic and thermal Free Energies [hartree] | -234.496058 | -234.499297 | -234.500104 | -234.498689 | -234.497438 | -234.497367 | -234.500861 | -234.500743 | -234.498073 | -234.499481 |
| Geometry Alteration* | a=-75.438 b=1.5355 | a=-65.028 b=1.5481 | a=-66.303 b=1.5500 | a=-61.949 b=1.55263 | a=-71.280 b=1.5421 | a=-70.237 b=1.5433 | a=-176.624 b=1.5477 | a= 180.000 b=1.5482 | a=-179.996 b=1.5292 | a= 178.091 b=1.5384 |
- a = dihedral angle of C2-C3-C4-C5, b = bond length of central C3-C4 bond
Comments
ENERGY For HF/3-21G, The isomer has lowest optimised total energy is the gauche conformation,(gauche-3 E= -231.69266 Hartrees), whereas for DFT/B3LYP/6-31G(d) optimisation, the lowest energy is the anti conformation (anti-2 isomer E=-234.61172 Hartrees). however, the differences in energy between them are quite small. The energy is affected by the steric factor and also the electronic interaction (CH-p interaction), although the anti structure is less sterically hindred than gauche since the two termical C=C groups are pointing away, but the gauche form is stabilised by an interaction between the p-electrons of the C=C bond and the close vinyl proton, which absence in anti-isomer due to increase the distance of CH and p-electrons.
The HF/3-21G optimisation cannot include any electron correlation and many electronic effects, including a possible CH-p interaction are not properly considered using this method, and so the calculation was dominated by the steric factor. Whereas in DFT/B3LYP/6-31G(d), as a higher calculation method and basis set were used, the electronic interaction was the major concern.
Frequency The frequency calculations are critical in order to confirm weither the structures have reached its energy minima or transition state. There is no imaginary frequency shown in each case, which means the structures have reached the bottom of their PES.
GEOMETRY The most important factor to consider the C3-C4 central bond length is the terminal s-cis vinyls as well as the conformation around it.
All the anti conformers have shorter C3-C4 bond length than gauche expect gauche-1. The largest bond length difference (0.0234Å) arises from anti-3 and gauche-4, where is also the largest difference in any two adjacent conformers. The shortest central bond C3-C4 is the anti-3 conformer, it is an anti conformer with two s-cis vinyls.. The second place is the gauche-1, which also has two s-cis vinyl groups. These conformers have only one s-cis vinyl group come to the third.
Optimizing the "Chair" and "Boat" Transition Structures
Optimisation of Chair Conformation
(A) Procedures
1. Optimisation of an allyl of CH2CHCH2. (HF/3-21G)
2. Duplication of optimised CH2CHCH2 in a new window and alterated to a chair conformation. The distance between the two fragments were fixed to be approximately 2.2Å and then optimised to a Berny transition state. (Opt+Freq, HF/3-21G, force contact=once, A.K.=”opt=noeigen”)
3. Defreezing the distance and optimisation again. (Opt+Freq, HF/3-21G, force contact=once, A.K.=”opt=noeigen”)
4. Optimisation to a higher basis set. (Opt+Freq, DFT/B3LYP/6-31G, force contact=once, A.K.=”opt=noeigen”)
(B) Results of Optimisations
(1) HF/3-21G basis set
Optimised electronic energy of chair = -231.619322
Sum of electronic and zero-point Energies= -231.466700
Sum of electronic and thermal Energies= -231.461340
Sum of electronic and thermal Enthalpies= -231.460396
Sum of electronic and thermal Free Energies= -231.495206
Distance of two fragments= 2.0205Å
(2) DFT/B3LYP/6-31G(d) basis set
Optimised electronic energy of chair = -234.556983
Sum of electronic and zero-point Energies= -234.414914
Sum of electronic and thermal Energies= -234.408993
Sum of electronic and thermal Enthalpies= -234.408049
Sum of electronic and thermal Free Energies= -234.443798
Distance of two fragments= 1.9667Å
Point Group= C2h
(C)Vibration Frequency
To confirm the molecule is in its transition state, an imaginary frequency was found at -565.396cm-1, by using animation, the movement of molecule corresponding to the imaginary frequency is shown below:
Optimisation of Boat (QST2 method)
- A different method was used from the optimisation of chair conformation, the QST2 method specifies the reactant and product as two independent inputs and then to estimate the mid-point between them, ie. the transition state. The approach of transition state optimisation is significantly different from previous one, as the reactant and product are not presented in a same window, the correct atom labelling is essential.
(A) Procedures
1. By using the two optimised anti-2 conformers, to generate and optimise the new molecule. (HF/3-21G)
The calculation was failed, this may due to the fragments in starting structure are too far off from its transition state. Since the failed the out. file strcutre shows a similar conformation of chair TS, the reason of failure may also came from the stored memory from previous chair TS calculation.
2. The inputs were then altered to a gauche conformation (shown as blow), and an optimisation was carried out. (Opt+Freq, QTS2, HF/3-21G, force contact=once, A.K.=”opt=noeigen”)
(B) Results of Optimisations
(1) HF/3-21G basis set
Optimised electronic energy of chair = -231.602802
Sum of electronic and zero-point Energies= -231.450928
Sum of electronic and thermal Energies= -231.445299
Sum of electronic and thermal Enthalpies= -231.444355
Sum of electronic and thermal Free Energies= -231.479119
Distance of two fragments= 2.1399Å
(2) DFT/B3LYP/6-31G(d)basis set
Optimised electronic energy of chair = -234.543093
Sum of electronic and zero-point Energies= -234.402340
Sum of electronic and thermal Energies= -234.396006
Sum of electronic and thermal Enthalpies= -234.395062
Sum of electronic and thermal Free Energies= -234.431094
Point Group = C2v
Distance of two fragments= 2.2064Å
(C)Vibration Frequency
To confirm the molecule is in its transition state, an imaginary frequency was found at -530.58cm-1. By using animation, the movement of molecule corresponding to the imaginary frequency is shown below:
Intrinsic Reaction Coordinate (IRC)
The optimised transition state of chair conformation was then calculated further by IRC, in order to track the reaction pathway. The IRC calculation optimises the structure at each stage of reaction and can perform in both directions (starting from the TS to the reactant/product), for the reaction concerned in this case, because it is symmetrical and so only the forward pathway needs to be calculated.
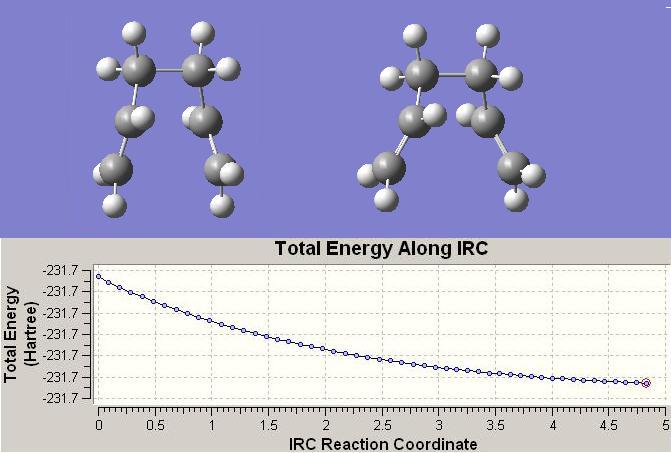
(A) Primary IRC calculation
Job Type: IRC
Follow IRC: Forward only
Calculate Force Constants: Once (Compute more points, N=50)
Calculation method: HF/3-21G
The LHS structure is the starting structure, and the RHS streucture is the IRC calculated 51st geometry.
E= -231.680544
Point Group= C2
When the primary IRC calculation finished, there are 51 intermediate geometries (contains the starting material) to present how the calculation pathway has progressed. The above IRC graph shows the starting and finishing structures of this calculation with its total energy in each step. The optimised energy in this case is still higher than previous calculated energy of optimised Gauch-1 conformer, since the it hasn't reached the minimum geometry yet, further IRC calculations were carried out using the no. 51 structure.
(B) Secondary IRC calculation
The secondary IRC calculation was carried out in three different settings (as layed out below).
(1) Energy Minimisation of Structure 51
Job Type: Optmisation
Calculation method: HF/3-21G
E= -231.691667 hartrees
Point Group= C2
Calculation Time= 0hrs 9min
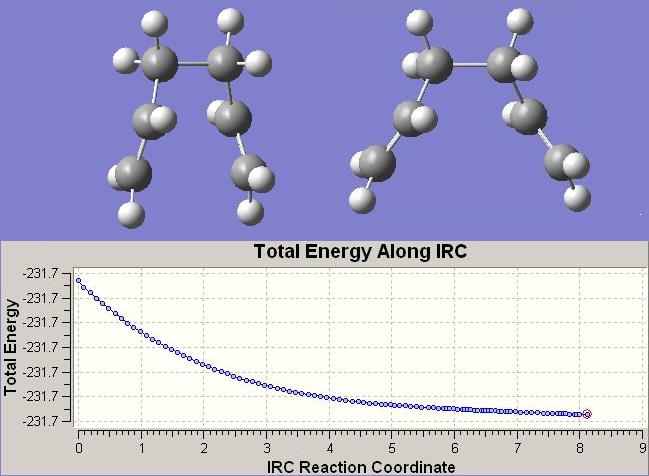
(2) Further IRC Calculation of Structure 51 (altering the Calculate Force Constants)
Job Type: IRC
Follow IRC: Forward only
Calculate Force Constants: Always (Compute more points, N=50)
Calculation method: HF/3-21G
The LHS structure is the starting structure, ie. the 51st geometry from primary optimisation, and the RHS streucture is the new IRC calculated 51st geometry.
E= -231.690566 hartrees
Point Group= C2
Calculation Time= 2hrs 15min
(3) Further IRC Calculation of Structure 51 (altering compute point)
Job Type: IRC
Follow IRC: Forward only
Calculate Force Constants: Once (Compute more points, N=100)
Calculation method: HF/3-21G
The LHS structure is the starting structure, ie. the 51st geometry from primary optimisation, and the RHS streucture is the new IRC calculated 100th geometry.
E= -231.691452 hartrees
Point Group= C2
Calculation Time= 2hrs 54min
(C) Comment
All the IRC calculations had relatively close optimised energies and the some point group of C2.
As the method used became more reliable theoratically, the calculation time required increased dramatically as a consequency of more accurate calculation.
The total optimised energy and point group of first methos in secondary optimisation is matched with the data of optimised Gauche-2 conformer, which means that the Gauche-2 conformer is involved in the Cope Rearrangement through chair/boat transition state.
Activation Energies
The activation energy of both chair and boat transition state structures at 298.15K are compared in HF/3-21G and B3LYP/6-31(d) basis sets, these computational results were then compared with experimental activation energies at 0K.
| Activation Energy (kcal/mol) | HF/3-21G at 298.15K | DFT/B3LYP/6-31G(d) at 298.15K | Experimental at 0K |
|---|---|---|---|
| ∆Ea – Chair Conformation | 44.7 | 34.04 | 33.5±0.5 |
| ∆Ea – Boat Conformation | 52.21 | 43.44 | 44.7±2.0 |
In general, the computational activation energies from B3LYP/6-31G(d) are mathched quite well with the experimental data, which suggests the higher accuracy level of better method and basis set.
Conclusion
The cope rearrangement of 1,2-hexadiene suggests the involvement of Gauche-2 conformation and this reaction should proceed through chair transition state, which has lower reaction barrier, ie. lower activation energy.
Reference
1. B.G.Rocque, J.M.Gonzales, H.F.Schaefer, Molecular Physics, 2002, vol.100, No.4, p 441-446
2. S.Sakai, Journal of Molecular Structure THEOCHEM, 2002, vol.583, issue 1-3, p 181-188
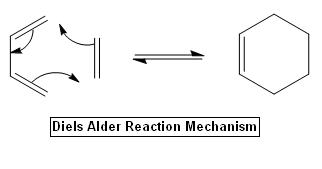
The Diels Alder Cycloaddition
The Diels-Alder cycloaddition is classified as a pericyclic reaction, the mechanism involves a conjugated diene reacting with a substituted alkene, e.g. dienophile, and generates a substituted cyclohexene system by forming two new sigma bonds.
The stereospecific formation of new sigma-bonds requires a firm HOMO and LUMO overlap, which contributed from two reactants each, and therefore, the correct symmetry orientation is essential in order to maximise the overlap. The major concern in this exercise is to study the structure of the single transition state.
Optimisation and MOs Generation of cis-butadiene
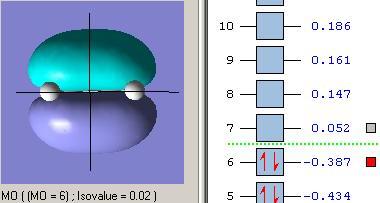
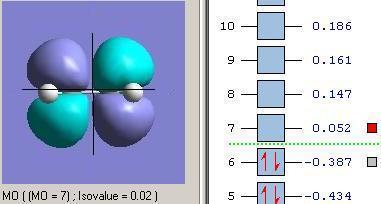
The prototype Diels-Alder cycloaddition involves reaction between cis-butadiene and ethylene, the orientations of HOMO and LUMO for both reactants are essential in order to anaylse the degree of overlap.
| Molecular Orbital | Quantitative Representation of MO | Qualitative Representation of MO | Symmetry of Horizontal Axis | Symmetry of Vertical Axis |
|---|---|---|---|---|
| HOMO of cis-butadiene |  |
 |
antisymmetric | antisymmetric |
| LUMO of cis-butadiene |  |
 |
antisymmetric | symmetric |
| HOMO of ethylene |  |
 |
antisymmetric | symmetric |
| LUMO of ethylyene |  |
 |
antisymmetric | antisymmetric |
In order to proceed the stereospecific Diels-Alder cycloaddition, the two overlapping orbitals (contributed from one reactant each) must have the same orientation. According to the table above, the HOMO of cis-butadiene and the LUMO of ethlyene have exactly the same orientation in both axis. And also, the ethylene is less electron-rich comparing with cis-butadiene, therefore, the interaction is more favourable between the HOMO of cis-butadiene and the LUMO of ethylene.
Endo vs. Exo Product
Due to secondary overlap between the reactants, formation of endo product is more favourable than exo product.
Transition State Geometry of Prototype Reaction
There are 6 pi-electrons involved in the Diels Alder cycloaddition of cis-butadiene with ethylene, and so this reaction has a suprafacial arrangement in its transition state in order to obey the Hückel's Law.
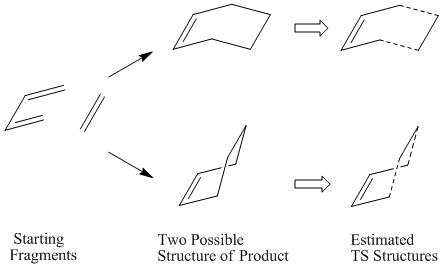
There are two possible TS generated as the stereospecific feature involved in the formation of new sigma-bonds, which determinated by the degree of interaction between HOMOs and LUMOs.
Optimisation of Transition State
The optimisation of transition state depends on the reaction pathway between HOMO-LUMO interaction of two reactants.
1. Optimising the endo/exo product, and the newly formed sigma-bonds were manually removed, the distance between the two fragments set to be 2.20Å. The modified envelope-like structure is shown below:
2. A frequency and optimisation calculation was carried out with above structure. (Opt+Freq, semi-empirical/AM1, force contact=always, A.K.=”opt=noeigen”)
The optimised the structure is shown in Jmol:
Geometry of Transition State
| Structure | Inter-fragment Distance (Å) | Dashed Double Carbon Bonds in cis-butadiene (Å) | Double Carbon Bonds in cis-butadiene (Å) | Double Carbon Bonds in ethene (Å) | Van Der Waal radius of Carbon Atom (Å) |
|---|---|---|---|---|---|
| Before Optimisation | 2.8923 | 1.3967 | 1.3618 | 1.3284 | - |
| After Optimisation | 2.1192 | 1.3975 | 1.3819 | 1.3829 | 1.70 |
The inter-fragments distances were changed from 2.21 Å to 2.12 Å by optimisation, consider the Van Der Waal radius of carbon atom(1.70 Å), this distance is shorter than two radius, this indicates a significant overlap between the terminal carbons of cis-butadiene and ethylene.
The dashed carbon double bond length of optimisied cis-butadiene is approximately 1.40 Å, which is shorter than the standard carbon single bond (1.54 Å) but longer than standard carbon double bond (1.34 Å), this also implies to the carbon doubles in both cis-butadiene and ethylene are a.c. 1.38 Å, these are the evidences of partial transformation from carbon double bond to single bond.
Vibrational Spectrum of Transition State
In order to confirm whether the structure is in its transition state or energy minima, the vibrational frequency calculation was carried out. One negative vibrational frequency at -955.641 cm-1 is shown in the spectra, this particular frequency does not have any physical sense, it is an imaginary frequency which generated from the algorithm calculation (how the programme functions), however, the motion of the imaginary frequency indicates the way of reaction approach. The formation of these two new sigma-bonds are synchrous, according to the motion of imaginary frequency.
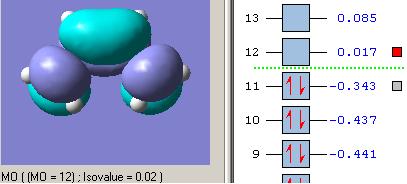
Molecular Orbitals of Transition State
The optimised structure of transition state was further calculated to obtain its molecular orbital representations of HOMO and LUMO. (Opt+Freq, TS (Berny), semi-empirical/AM1, force contact=once, A.K.=”pop=full”)
| Molecular Orbital | Quantitative Representation of MO | Qualitative Representation of MO | Symmetry of Horizontal Axis | Symmetry of Vertical Axis |
|---|---|---|---|---|
| HOMO of TS |  |
 |
antisymmetric | antisymmetric |
| LUMO of TS |  |
 |
antisymmetric | symmetric |
Now consider the symmetries of vertical axis for each fragments and transition states. As expected, the HOMO of TS (asymmetric) structure is formed by HOMO of cis-butadiene (asymmetric) and LUMO of ethylene (asymmetric), and the LUMO of TS (symmetric) structure is formed by LUMO of cis-butadiene(symmetric) and HOMO of ethylene (symmetric) as they have the same orientation respectively.
Therefore, the overlap was formed well and the generation of product from Diel-Alder reaction should be successful.
Study of Regioselectivity of the Diels-Alder Reaction
The cycloaddition of substituted diene, cyclohexa-1,3-diene and dieneophile, maleic anhydrid was concerned in this part. By considering the transition state, the one with lower energy is more likely to be form, and so the endo product is favoured thermodynamically. However, the exo product can still formed even the transition state structure is not in the correct orientation to interact. Therefore, in order to determine the regioselectivity of this reaction, the energy, geometry, vibrational frequency and molecular orbital were studied.
The endo structure will be formed as the major product, whereas the exo struture is the minor.
Optimisations of Endo and Exo Transition States
Procedure of endo/exo product
1. The cyclohexa-1,3-diene and maleic anhydride reacting fragments were set up manually in a way of endo/exo geometry, then optimisation was run. (Opt, minimum, semi-emperial/AM1)
2. The formed inter-fragments bond was broken manually, and the distance between the two fragments were frozen to be approximately 2.09Å, an optimisation calculation was run. (Opt+Freq, TS (Berny), semi-emperial/AM1, force contact=always, A.K.=”opt=noeigen”)
3. The inter-fragements distance of optimised structure was then defreezed, and optimisation was carried out again.
(Opt+Freq, TS (Berny), semi-emperial/AM1, force contact=always, A.K.=”opt=noeigen”)
Optimised Structure of endo and exo
The optimised TS endo structure in Jmol:
The optimised TS exo structure in Jmol:
Energies of Endo and Exo Transition States
E (TS of Endo) = -0.05159430 a.u.
E (TS of Exo E) = -0.05050326 a.u.
E (Product of Endo) = -0.16023162 a.u.
E (Product of Exo) = -0.15996743 a.u.
Both of optimised transition state and product energies of endo are lower than exo-structure, which suggest that the endo structure is favoured in both thermodynamically and kinetically ways, ie. the lower energies required in formation of final product and transition state. The transition state and product of exo structure were destabilised by steric repulsion between the maletic anhydride and the -CH2-CH2- fragment from cyclohexa-1,3-diene. Furthermore, the transition state of endo structure was stabilised by 2° orbital interaction, whereas in exo structure, these two fragments of transition state did not have the right orientation to interact.
Geometries of Endo and Exo Transition States
| Structure | Inter-fragment Distance (Å) | C1-C4 Dashed Double Bond in Cyclohexa-1,3-diene (Å) | C1-C2 & C4-C6 Dashed Double Carbon Bonds in Cyclohexa-1,3-diene (Å) | C3-C5 Dashed Double Bond in maleic anhydride (Å) |
|---|---|---|---|---|
 endo |
2.6351 | 1.3968 | 1.3944 | 1.4101 |
 exo |
2.7065 | 1.3972 | 1.3931 | 1.4085 |
The inter-fragments distance of endo is a.c. 0.07Å shorter than exo structure, which favours the formation of transition state of endo structure.
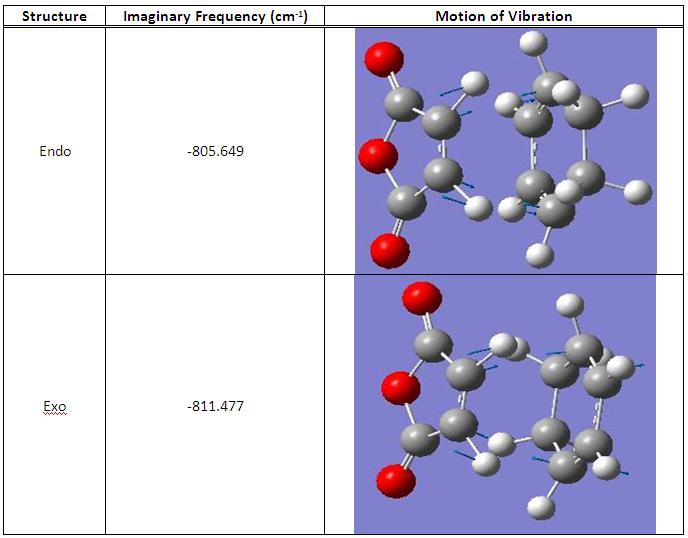
Vibrational frequencies of Endo and Exo Transition States
Similarly to the previous part anaylsis, both endo and exo transition state show one imaginary frequency in the vibrational spectrum, which proves that the formations of both transition state were successful.
Molecular Orbitals of Endo and Exo Transition States
The optimised TS endo/exo structures were further calculated to obtain its molecular orbital representations of HOMO and LUMO.
(Opt+Freq, TS (Berny), semi-empirical/AM1, force contact=once, A.K.=”opt=full”)
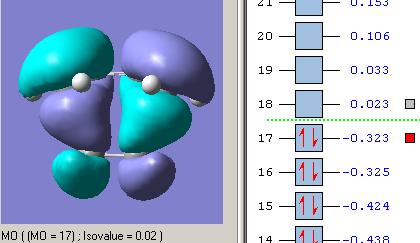
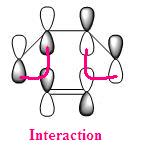
As explained perviously, the transition state of endo and exo have different orientations, and so the HOMO interaction of each structure are diffenrent as well. From the quantitative and qualitative HOMO representations BLOW, we can see that the endo structure has the right orientation and it can be stabilised by a secondary orbital overlap effect, which contributed by the pi-system of "-HC=CH-" unit from cyclohexa-1,3-diene and "-C=O-CO-C=O" unit in maleic anhydride, whereas the exo TS structure could not have this overlap due to incorrect orientation.
| Molecular Orbital | Quantitative Representation of MO | Qualitative Representation of MO |
|---|---|---|
| HOMO of ENDO TS |  |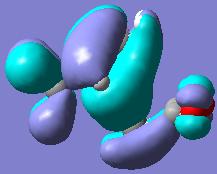
 |
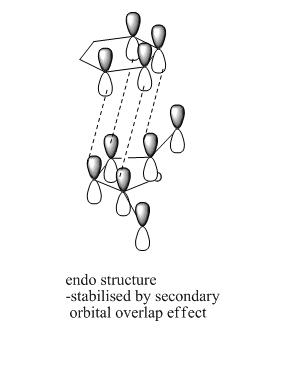| HOMO of EXO TS |  |
 |
Overall, the endo TS is favoured than exo TS due to sterically less hindred together with the secondary orbital overlap stabilisation.
Conclusion
The Diels-Alder reaction is proceeded to the endo structure product via endo transition state, as the endo is kinetically and themodynamically favoured than exo in both energy minima and TS structure.
Reference
1. Diels Alder reaction (http://en.wikipedia.org/wiki/Diels_Alder)
2. Carbon Van Der Waal radius (http://en.wikipedia.org/wiki/Carbon)