Rep:Mod:cjmk1956
All energies are given in units of hartrees. Example reaction schemes were taken from original 'wiki' page: http://www.ch.ic.ac.uk/wiki/index.php/Mod:organic
Hydrogenation of Cyclopentadiene Dimer
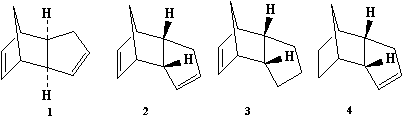
When Cyclopentadiene dimerises, via a [4+2] cycloaddition, the product is either in the endo (2) or exo (1) form. By analysing the torsion angle of the two groups an estimate of the thermodynamically stable structure can be made. Structure 1 has a torsions angle of 180° while structure 2 has an angle of 51.7°. The two connecting carbons would prefer to have the large substituents in the anti-periplanar arrangement, at 180°, to reduce strain and prevent steric interaction between the two groups. Structure 2 has a particularly acute angle, increasing the strain on the two connecting carbons, and so is thermodynamically less stable than structure 1 which displays anti-periplanar arrangement. This is quantified by contributions to the overall energy as shown below. The more favoured anti-periplanar arrangement, lowers the torsional strain and therefore minimises the total energy of structure 1. The exo form (1) is 0.0508 hartree to the 0.0542 hartree of the endo form (2). It is known however that more of the endo product is formed. With investigation of the transition states of both products, the endo TS is far more stable than the exo TS. As a result the endo form is kinetically favoured and produced as the main product.

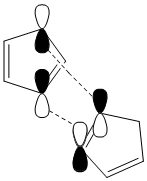
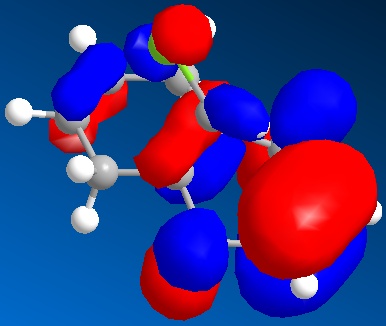
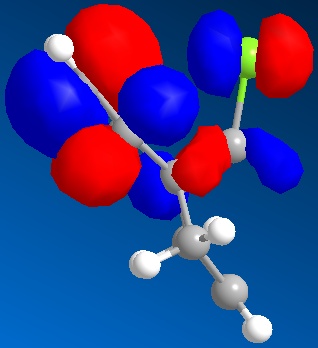
The endo TS, left, contains orbitals on both monomers of the correct symmetry which enables bond formation. Unlike the exo TS, right, as the monomers are more ‘in line’ with each other the remaining ring orbitals can participate in non-bonding or 'secondary' interactions with similar orbitals on the other monomer, which increases overall stability of the transition state. Less important is the compact nature of the endo TS compared with the exo TS, which may also add to its increased stability.
Hydrogenation of the cyclopentadiene dimer proceeds to yield derivatives 3 and 4. From MM2 calculations, structure 4 is the thermodynamically stable product. Below are the specific contributions to the Energy Minima of Structures 1,2,3 and 4.
| Energy Type (hartree) | Structure 3 | Structure 4 | Structure 1 | Structure 2 | |
|---|---|---|---|---|---|
| Stretching (str) | 1.94E-03 | 1.75E-03 | 2.06E-03 | 1.99E-03 | |
| Bending (bnd) | 3.00E-02 | 2.31E-02 | 3.28E-02 | 3.31E-02 | |
| Torsion (tor) | 1.94E-02 | 1.99E-02 | 1.22E-02 | 1.52E-02 | |
| van de Waals (vdw) | 9.16E-03 | 7.19E-03 | 6.74E-03 | 6.92E-03 | |
| H-bonding (H-bond) | 2.60E-04 | 2.25E-04 | 6.02E-04 | 7.95E-04 | |
| Overall Energy | 5.72E-02 | 4.97E-02 | 5.08E-02 | 5.42E-02 |
When structure 2 is hydrogenised, it can occur at either of the two double bonds; which one, depeneds upon the stability of the double bond. Investigation reveals that the double bond on the right of the molecule as shown in structure 2 above, exhibits a bond angles of 112.3° (between C3 and C5)and 113.2° (between C2 and C4). This is close to the optimised angle of 120° for a sp2 hybridised carbon. The double bond however exhibits angles of 107.6° (between both C6, C8, C9 and C7, C8, C9). Therefore the bond is further away from its preferred angle and less stable, being more prone to hydrogenation than the other double bond. Also, for what may be deemed an ominous characteristic, its angle of 107.6° is very close to the preferred angle of a sp3 carbon, which is 109.5°. Therefore the carbons in this double bond have even more of an affinity to become hybridised to this state.
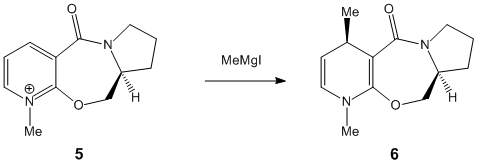
Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)
MM2 calculations were carried out for both the starting molecules above. Initially values were given that seemed excessively large (around 7.97E-02 hartree) so analysis of the molecule in terms of altering the orientation of certain groups was performed to attain lower values. In particular for molecule 5 the carbon to the right of the ring oxygen (as shown in the diagram above) was moved up, and the oxygen moved down so that they were closer. This adjustment caused the energy to fall to 4.05E-02 hartree. Perhaps this was due to the fact that the lone pair on the oxygen was further away from the methyl group on the pyridine, preventing a destabilising interaction.
NAD 5 |
Compound 5
NAD 7 |
Compound 7
Similarly the methyl group in the 7 membered ring of molecule 7 was moved to the possibly more axial position on the ring carbon. This resulted in the group avoiding steric hinderance with the iso-propyl group on the ring nitrogen. As a consequence, the MM2 calculation produced a minimum of 2.44 hartree.
The orientation of the carbonyl group differs between molecule 5 and 7. In molecule 5, assuming the carboxyl carbon is co-linear with the benzene group, the torsion angle between the oxygen and the ring is 41.9°. Conversely, in molecule 7 the torsion angle is -42°, i.e. in the opposite direction. Therefore when comparing the molecules the carbonyl groups point in opposing directions.
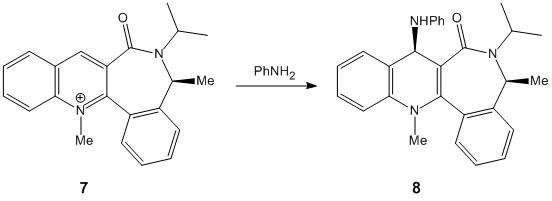
This causes stereochemical ramifications when there is an addition to the pyridine ring in the. It must first be pointed out though that as all the other positions are protected and/or fused the only readily available carbon for addition is the one para to the pyridine-N. In molecule 5, the methyl group adds via co-ordination of the Grignard reagant to the amide oxygen. There is subsequent conjugate delivery of the methyl group and because the carbonyl group is facing 'up' with respect to the planar ring, the methyl group will be added in this same orientation. In molecule 7 however as there NPhH2 is this time being added, there is no co-ordination this time with the carbonyl oxygen. In fact the lone pairs on the Oxygen repels the lone pair on the Nitrogen and as a result the group adds to the planar ring on the opposite side of the ring to the carbonyl and therefore in the opposite orientation. As stated earlier the carbonyl group in molecule 7 is orientated in the opposite direction to the same group in molecule 5. Therefore when NPhH2is added in the opposite orientation to the carbonyl group it ironically results in both the addition groups of molecules 5 and 7 being orientated in the same direction! Use the jmol application above to become familiar with the orientation of the carbonyl groups and to visualise the mechanism of addition in both cases.
Literature
1. A. G. Shultz, L. Flood and J. P. Springer, J. Org. Chemistry, 1986, 51, 838
2. S. Leleu; C. Papamicael; F. Marsais; G. Dupas; V. Levacher. Tetrahedron: Asymmetry, 2004, 15, 3919-3928
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
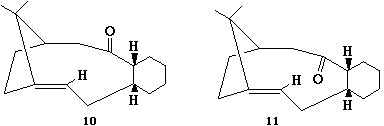
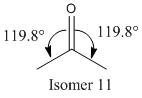
Isomers 10 and 11 show a deviation in the orientation of the carbonyl oxygen. Isomer 10 has the carbonyl pointing 'up', where up is defined as the same direction as the α, β hydrogens in the fused cyclohexane ring. Isomer 11 has the carbonyl oxygen pointing down, in the opposite direction. See the jmol applications below.
Taxol 10 most stable with adjustment 44 |
Compound 10
Taxol 11 chaz |
Compound 11
| Energy Type (hartree) | Carbonyl Up (Isomer 10) | Carbonyl Down (Isomer 11) | |
|---|---|---|---|
| Stretching (str) | 4.96E-03 | 4.05E-03 | |
| Bending (bnd) | 3.27E-02 | 1.74E-02 | |
| Torsion (tor) | 3.51E-02 | 3.12E-02 | |
| van de Waals (vdw) | 2.28E-02 | 2.01E-02 | |
| H-bonding (H-bond) | 2.39E-05 | -2.87E-04 | |
| Overall Energy | 9.53E-02 | 7.06E-02 |
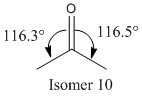
As shown above, isomer 11 is the more thermodynamically structure. This is due to the fact that the bond angles of the carbonyl group is much nearer the optimum value of 120° for an sp2 hybridised carbon.
When the intermediate is hydrogenated and the alkene of the 9 membered ring is lost, the reaction proceeds very slowly. This is because there is a reluctance to lose the alkene within the ring. As the ring contains a chair conformation cyclohexane ring fused to it, there is considerable strain added to the already strained 9 memebered ring. As a result, the carbons within cannot sustain the preferred 3 bond angle of 109.5° and deviate markedly from it by actually being closer to 120°. However as an sp2 hybridised alkene prefers a 120° bond angle it means that it is less strained within the ring as compared to a sp3 hybridised carbon. Furthermore when the hydrogenation occurs the result is added transannular strain from the added hydrgogens. These factors and up to why in fact the alkene in the 9 membered ring is hyperstable, and so reacts slow when under hydrogenation conditions
When the hydrogenation product was first minimised the overall energy was 8.67E-02 hartree. Again when the oxygen was placed in the 'down' position the energy was reduced again to 8.22E-02 hartree. Also the cyclohexane ring was placed in the chair conformation, the energetically preferred conformation, to further minimise the overall energy.
Literature
1. S. W. Elmore and L. Paquette, Tetrahedron Letters, 1991, 319;
How one might induce room temperature hydrolysis of a peptide
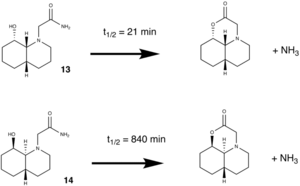
The two isomers, 13 and 14, had the respective orientations of the N-substituent altered and their MM2 energies calculated.
| Isomer | Axial Conformer Energy (hartree) | Equitorial Conformer Energy (hartree) |
|---|---|---|
| Isomer 13 | 4.73E-02 | 2.66E-02 |
| Isomer 14 | 4.03E-02 | 1.54E-02 |
As can be seen the equitorial arrangement of the amide substituent is the more favoured conformation, i.e. a greater amount will be present in equilibrium. For esterification to proceed as above, isomer 13 needs the amide substitiuent to be in the equitorial conformation, which then allows the hydroxy group to attack the amino-nitrogen. However, isomer 14 on the other hand needs the amide substituent to be in the axial conformation for the reaction to proceed. As the equitorial conformation is in greater abundance and/or more favoured in both isomers, isomer 14 will have a longer half-life than 13 because it will have to revert to it's axial conformation to proceed in the reaction. 13 need not do this and so will proceed in the reaction quicker.
NB In the equitorial conformer of isomer 13, an original energy was calculated at 2.96E-02 hartree. To minimise this further the hydrogens on the amine were brought closer to the hydroxy group to in effect increase the strength of the H-bonding and therefore decrease the overall energy. This was attempted for the other structures, but due to their respective conformations, the hydrogens were too far away at optimum geometry to increase the dipole-dipole interaction.
These peptides do not take 500 years to hydrolise like most straight-chained peptides because these peptides are rings. Therefore there is no free rotation of bonds which can place the reactive groups further away in an unreactive state, which can occur in straight chained peptides and results in a long reaction time for hydrolysis. Furthermore, the fact that there is hydrogen bonding in this molecule means that the ring is locked in the conformation that allows the reaction to proceed quickest, i.e. that the reactive groups are closer together.
Literature
1. M. Fernandes, F. Fache, M. Rosen, P.-L. Nguyen, and D. E. Hansen, 'Rapid Cleavage of Unactivated, Unstrained Amide Bonds at Neutral pH', J. Org. Chem., 2008, 73, 6413–6416
Modelling Using Semi-empirical Molecular Orbital Theory - Regioselective Addition of Dichlorocarbene
Both molecules above were minimised using the MM2 method and secondly using the quantum mechanical HF/STO-3G self-consistent field MO method. The MM2 method showed how the hydrogenation of the double bond anti to the chlorine atom affects the geometry of the molecue.
Di-alkene (Compound 15) Mono-hydrogenated Derivative (Compound 16)
In the di-alkene (above left) it can be seen that the cyclohexene groups are near planar, with the top and bottom carbons slightly below the plane of the rings. Comparatively, the corresponding diene, 2,5-cyclohexa-di-ene, is planar when MM2 minimised, therefore it can be said that the bridging group has a slightly distorting affect upon C2 and C5. When the double bond anti to the chlorine is hydrogenated however (compound 16), the conformation of the respective ring alters (above right). What can be seen is that the ring is now in the highly energetic half-chair conformation, commonly known as the envelope. This is due to the fact that the now sp3 hybridised carbons need to accomodate themselves in the preferred 109.5°, while two of the other carbons in the ring need to remain at 120° as they are still sp2 hybridised. Four of the carbon atoms are on the plane, of which the two bonds are fully eclipsed. As a result of this torsional strain, the torsion energy is increased and therefore the overall energy is increased also, as tabulated below.
| Energy Type (hartree) | Di-alkene (Compound 15) | Mono-hydrogenated Derivative (Compound 16) | |
|---|---|---|---|
| Stretching (str) | 9.86E-04 | 1.44E-03 | |
| Bending (bnd) | 7.57E-03 | 7.46E-03 | |
| Torsion (tor) | 1.22E-02 | 1.72E-02 | |
| van de Waals (vdw) | 9.26E-03 | 1.12E-02 | |
| H-bonding (H-bond) | 1.78E-04 | 1.12E-04 | |
| Overall Energy | 2.85E-02 | 3.55E-02 |
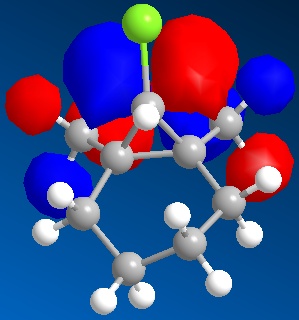
When the HF/STO-3G self-consistent-field MO method was applied, the molecular orbitals of both compounds 15 and 16 could be attained. Below are the representations of the selected molecular orbitals of compound 15.
HOMO-1 HOMO LUMO
LUMO+1 LUMO+2
Below are the representations of the selected molecular orbitals of compound 16
HOMO-1 HOMO LUMO
LUMO+1 LUMO+2
When addition is considered to the initial diene, regioselectivity may be dictated in terms of either hyperconjugation or electrostatic effects or perhaps a combination of both. The treatment of the wavefunctions of valence electrons via the quantum mechanical HF/STO-3G self-consistent-field MO method allows one to analyse the molecular orbitals in the HOMO/LUMO region and from here speculate which interactions favour which groups, which therefore results in the discovery of regio-isomeric preference.
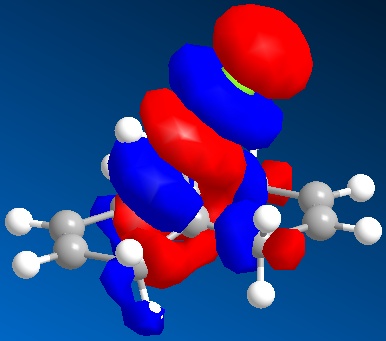
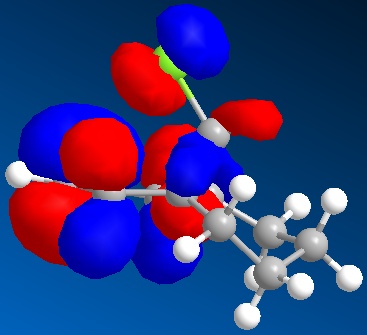
The Cieplak model relates to the interaction of a σ orbital and a σ* orbital and the concurrent regio-selectivity because of it. However this cannot be attributed in this case as both alkene groups have σ orbitals anti-periplanar to a σ* orbital. This means further investigation as this particular model is a common explanation of regio-selection. By analysing the orbitals of compound 15 as above it can be seen that the C-Cl σ* orbital (LUMO+2) is in fact anti-periplanar to the π-orbital of the exo alkene HOMO-1. This results in a favourable hyperconjugative interaction between the two, not unlike the Cieplak model; however it does not occur in the endo π-orbital because it is not anti-periplanar to the C-Cl σ* orbital. This causes a stabilisation of the exo π-orbital meaning it is less preferred to be attacked. Not only does the interaction cause greater stabilisation, it also causes electron density to become reduced in the exo π-orbital as compared with the non-interacting endo π-orbital. Rzepa et al quantify this consequence by stating that the pπ-orbital co-efficient of the exo alkene is 0.54 as compared to 0.58 for the endo alkene and this can be seen by comparing the endo π component in the HOMO with the exo π component in the HOMO-1(above). Therefore it can be said then that the endo alkene, with greater electron density, is more susceptible to electrophilic attack.
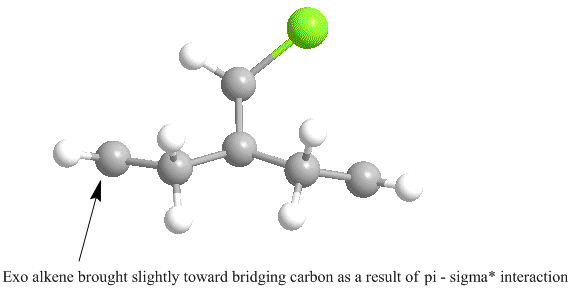
Furthermore, as a result of this C-Cl σ* - exo π-orbital interaction, there is a distortion of the exo C=C bond as compared with the endo C=C bond. The distortion in fact is a bringing forward of the C=C bond towards the bridging carbon obove the two cyclohexadiene rings. This can be seen primatively diagram below, which is an optimised structure. The slight bringing forward of the exo C=C bond does bring about a slight preference of the exo alkene over the endo alkene in terms of the original Cieplak model in that it's σ orbital can have a greater interaction with the antiperiplanar C-Cl σ* orbital. However this increased interaction is not as great as the observed π - σ* interaction and so addition to the endo alkene is still observed.
Vibrational Frequencies of Compounds 15 and 16
Both compounds display C-Cl stretch vibrations. Compound 15 displays this at 772.6cm-1 while compound 16 shows close to this at 776.8cm-1. When analysing the vibrations, there were many frequencies which included vibrations that affected the C-Cl bond so determination of the exact frequency proved to be open. However the greatest intensity of these was observed at the given frequencies, as was the most obvious C-Cl vibrations from the animated vibrations in GaussView.
The C=C bond vibrations were more obvious due to the intense action that resulted upon the ring. In compound 15 there were two frequencies for the two C=C bonds. The exo C=C bond had a vibration a 1740.7cm-1 whilst the endo bond had a frequency at 1760.9cm-1. As they are both on equivalently numbered carbons in the two rings one may be forgiven for assuming that both would have identical frequencies. However via the analysis of orbital interactions as above, one can explain why there is a deviation. As mentioned the interaction between the exo π-orbital and the C-Cl σ* reduces electron density at the exo C=C π-orbital. Therefore it can be said that the bond order of the exo C=C bond is reduced as compared with the endo equivalent. Reduced bond order results in a lower frequency as the vibration of the bond in question is intrinsically altered by the order or strength of the bond. This observation concurs with the analysis of the molecular orbitals as above.
This part of the investigation was via a quantum mechanical method, namely the Density-functional B3LYP/6-31G(d) method. This takes into account the real life movements, specifically vibrations, stretches and bends, of the bonds within a molecule. The HF/STO-3G approach was also quantum mechanical but gave an insight in to the molecular orbitals and possible interactions of a molecule rather than vibrations. However a combination of the two enriches both routes of analysis, as can be seen in the determination of vibrational frequencies. The MM2 method was a classical mechanical method and aided in providing a optimised geometry of the structure which was the basis for the more explicit and in-depth investigations of quantum mechanical methods, which on its own classical mechanics cannot predict.
Literature
1. B. Halton, R. Boese and H. S. Rzepa., J. Chem. Soc., Perkin Trans 2, 1992, 447
2. A. S. Cieplak, B. D. Tait and C. R. Johnson, J. Am. Chem. Soc., 1989, 111,8447
3. W. E. Parham, D. A. Bolon, E. E. Schweizer, J. Am. Chem. Soc., 1961, 83, 603
Structure based mini-project using DFT-based Molecular Orbital methods
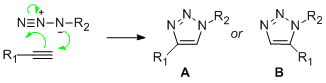
The area of analysis for specific investigation is so-called 'Click-Chemistry'. This is of interest as it provides the synthetic chemist the power to tailor useful compounds, such as hetero-rings, from initially small and relatively striaght-forward building blocks. The reaction in question relates to the ring formation of a tri-azole from a straight-chained alkyne and azide. As both components are substituted, one phenyl and one benzyl respectively, the attribute of regioisomerism arises.
Isomer A relates to 1,4-Regioisomer and Isomer B related to the 1,5-Regioisomer.
By using the Density-Functional Theory method, a quantum mechanical approach by trade, the 13C NMR Spectra of both isomers can be predicted which in turn can be analysed to differentiate them.
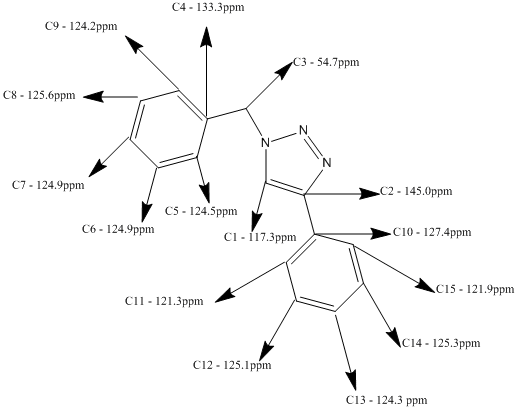
Below is the predicted NMR for the 1,4-Regioisomer, method and basis set: mPW1PW91/6-31G(d,p). Solvent: CDCl3
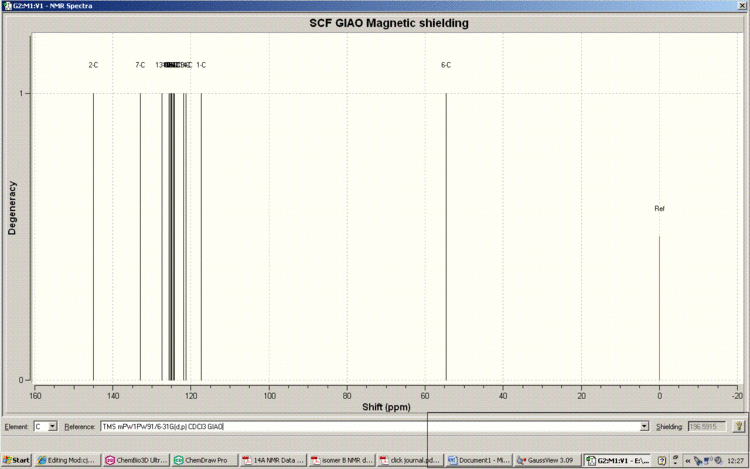
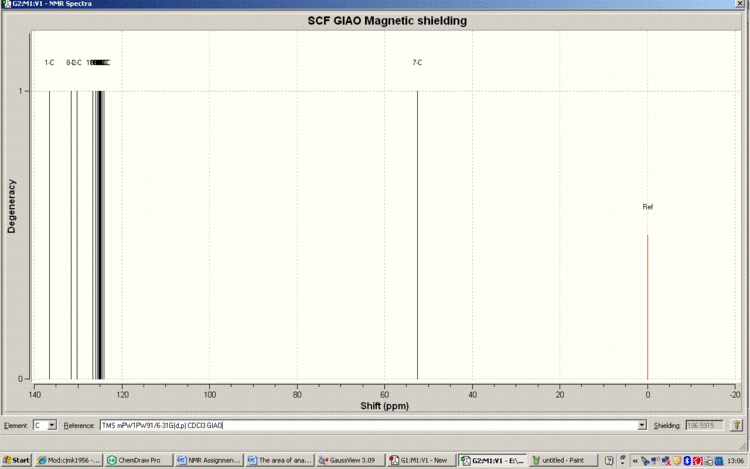
Tabulated Results of Computational Prediction: 13C NMR (TMS mPW1PW91/6-31G(d,p) CDCl3 GIAO) δ ppm – 145.0, 133.3, 127.4, 125.6, 125.3, 125.1, 124.9, 124.9, 124.5, 124.3, 124.2, 121.9, 121.3, 117.3, 54.7
Below is the Spectrum, zoomed in on the crowded region 120-130ppm.
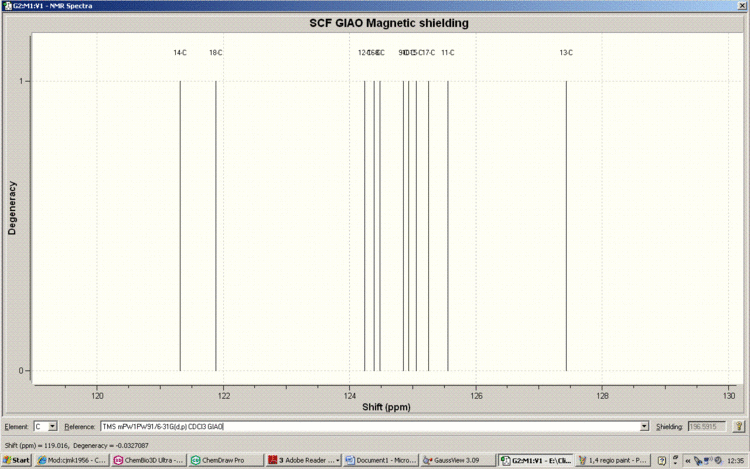
Here is the structural assignment for each of the 15 carbons of the 1,4-Regioisomer.
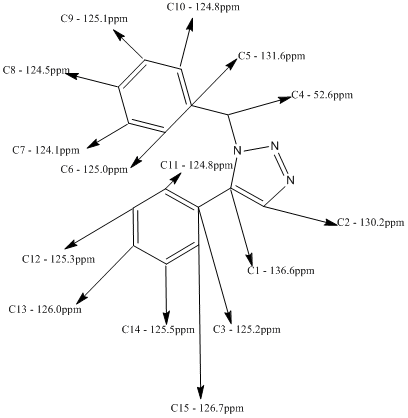
Below is the predicted NMR for the 1,5-Regioisomer, method and basis set: mPW1PW91/6-31G(d,p). Solvent: CDCl3
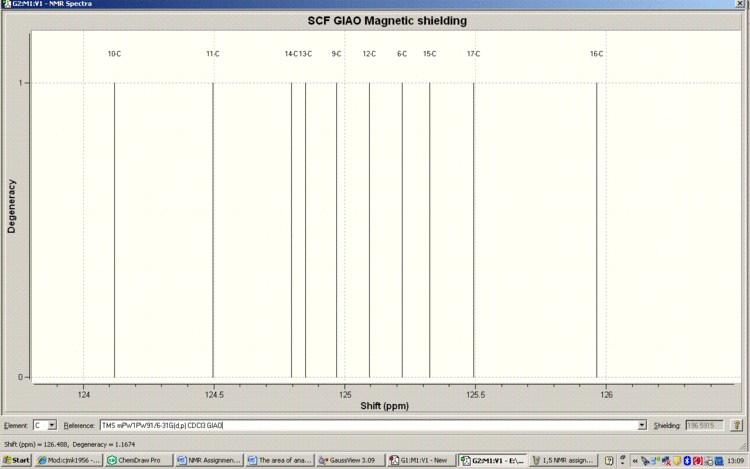
Tabulated Results of Computational Prediction: 13C NMR (TMS mPW1PW91/6-31G(d,p) CDCl3 GIAO) δ ppm – 136.6, 131.6, 130.2, 126.7, 126.0, 125.5, 125.3, 125.2, 125.1, 125.0, 124.8, 124.8, 124.5, 124.1, 52.6
Below is the Spectrum zoomed in on the crowded region 124-126ppm
Here is the structural assignment for each of the 15 carbons of the 1,5-Regioisomer.
If these predictions were to be used in the analysis of the two regioisomers then we can infer that they could be told apart by the respective shifts of the unsubstituted triazole carbon (i.e carbon without the phenyl group upon it).
For example in the 1,4 isomer (A), this carbon has a shift of 117.3ppm. In the 1,5 isomer (B), the unsubstituted carbon has a shift of 130.2ppm. This is quite a significant change and is endemic of the regioisomeric difference between the two. The theory behind this change in ppm is the location of the unsubstituted carbon in both structures. Isomer B is located next to a nitrogen wherein it's lone pair is not delocalised within the aromatic triazole ring, rather it is localised in the sp2 hybrid orbital. This lone pair displays a deshielding affect upon the unsubstituted carbon which as a result increases it's chemical shift. Comparatively, the unsubstituted carbon in isomer A is next to an environment wherein the nitrogen's lone pair is delocalised in the aromatic ring quintet, and so cannot exert a similar deshielding effect upon the unsubstituted carbon's chemical shift.
This seems the most obvious sign of distinction between the two isomers, as the chemical shifts of the other carbons in the molecule do not seem to differ on the scale of the unsubstituted carbon. Furthermore complete reliance of phenyl chemical shifts for isomeric determination would be an implausible route, given the unpredictability of this area.
The literature NMR spectra were found for both isomers and are cited.
1,4-Regioisomer Literature Result: 13C NMR (CDCl3, 50 MHz) δ ppm - 148.0, 134.6, 130.4, 128.9, 128.64, 128.56, 127.9, 125.5, 119.5, 54.0
1,5-Regioisomer Literature Result: 13C NMR (CDCl3, 126 MHz) δ ppm - 138.2, 135.5, 133.3, 133.3, 129.5 , 128.9, 128.9, 128.8, 128.2, 127.2, 126.9, 51.8
When compared to each other, the predicted NMR spectra correlate with their respective literature results i.e one could determine the predicted and literature spectra of each isomer. However there are acute dfferences between the literature and the prediction. For example in the 1,4 isomer there is an extra peak around 121ppm absent in the literature and a peak at 130ppm in the literature absent from the prediction.
Similarly in the 1,5 isomer there are literature peaks at 133pm not present in the prediction, and peaks at 124ppm from the prediction which are not present in the literature.
All of these differences relate to carbon peaks in either the phenyl or benzyl rings.
A key difference in the computational predictions is that they legislate for every carbon atom in the structures. The literature spectra on the other hand do not, due to overlapping of peaks with similar chemical shifts. Therefore some carbons are not legislated for in the literature. The overlapping is a reality of NMR spectroscopy and can cause great difficulty when assigning peaks in cutting-edge molecules. Therefore the fact that the computational NMR prediction is limited in recognising the realities of NMR spectroscopy can actually enhance a chmeists analysis of a molecule.
IR Spectra of Regioisomer A and B
Below is the IR spectra of the 1,4-Regioisomer
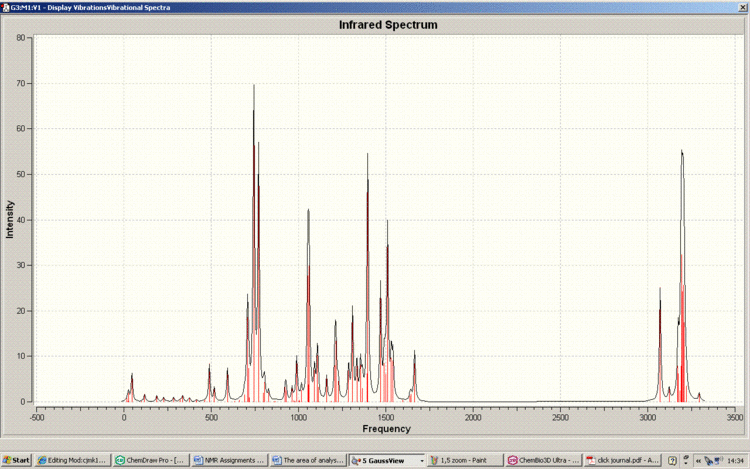
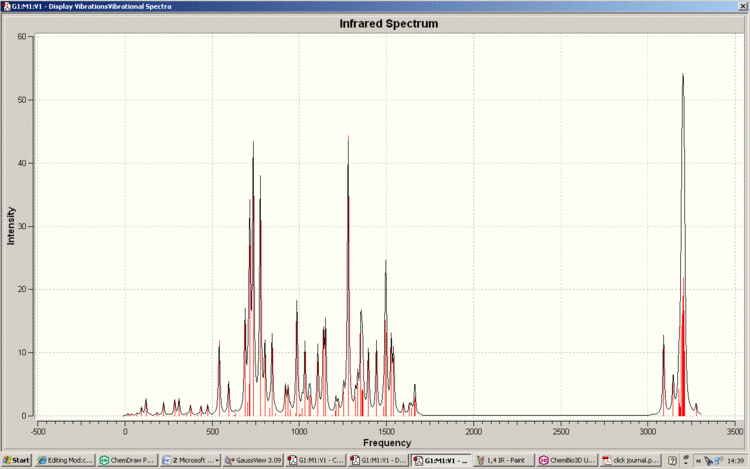
As can be seen, the IR spectra for the isomers are similar. This correlates with the fact that the functionality of the isomers are the same; it is only the connectivity which differs. Therefore NMR spectroscopy is the vital technique when analysing the isomerism of the reaction in question. This is also reflected in the fact that there are no literature IR results to compare with.
The coupling constants of 1H NMR were decided not be found using 'Jannochio' as there were deemed ineffectual for the analysis in this mini-project. This was because they would only relate to the hydrgoens on the benzene rings as these are the only hydrogens that can undergo 3J coupling. By analysing the 3J coupling constants in the literature below, it was found that there was no use in computing the predicted values as they would not aid in the above proposal of how to differntiate between the regioisomers spectroscopically.
This concludes the investigation into regioisomeric analysis of 1,2,3 triazoles using DFT-based molecular orbital methods.
Literature
1. B. Sharpless et al, J. Am. Chem. Soc. 2005, 127, 15998
2. NMR of 1,4 -Regioisomer - U Sirion, B. Se Lee, D. Yoon Chi, Ionic Polymer-supported CuI: A Reusable Catalyst for Huisgen’s 1,3-Dipolar Cycloaddition - Supporting Information, http://www.thieme-connect.com/media/synlett/EFirst/supmat/sup_u02708st-10-1055_s-2008-1078245.pdf
3. NMR of 1,5 Regioisomer - S. Chuprakov, N. Chernyak, A. S. Dudnik, V. Gevorgyan, Org. Lett., 2007, 9, 2333-2336.
4. V. N. Kizhnyaev, F. A. Pokatilov, N. A. Tsypina, G. V. Ratovskii, L. I. Vereshchagin, A. I. Smirnov, Synthesis of N-Vinyl-1,2,3-triazole Derivatives, Russian Journal of Organic Chemistry, 2002, 38, 7, 1056-1059