Rep:Mod:cjc415 TS
Introduction
This wiki explores a variety of pericyclic reactions, namely Diels-Alders and Cheletropic reactions and their transitions states.
Potential energy surfaces (PES)
A potential energy surface gives the energy of a molecule as a function of its geometry. It serves as a tool to help in the analysis of reaction dynamics and molecular geometry. The PES has a total of 3N-6 degrees of freedom.
At the stationary points, the gradient is equal to zero. These energy minima correspond to the physically stable species, such as reactants and products while transition states correspond to saddle points. When the second derivative is calculated, the energy minima and transition states can be differentiated. If a positive value is obtained, it suggests that an energy minima is obtained. Conversely, a negative value corresponds to a transition state.
This is also reflected in Gaussview. A transition state would produce one negative frequency while minima points will not reflect negative values, hence no imaginary frequencies are present.
Nf710 (talk) 21:28, 21 March 2018 (UTC) what you are actually doing is finding the eigenvalues of the hessian which relate to the force constants. each one relates to a dimension of the PES. a TS only has 1 negative force constant.
What is a transition state?
A transition state (TS) is usually defined as a structure along the reaction coordinate which corresponds to the highest potential energy along this coordinate. In terms of mathematics, the TS of a chemical reaction represents a Saddle Point on the Potential Energy Surface (PES).
A transition state of a reactive pathway is the one with lowest energy compared to other paths perpendicular to it. It is also the highest energy point of that reactive pathway.
Diels Alders reaction
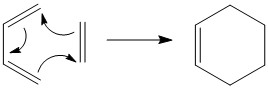
Otherwise known as a [4+2] cycloaddition, the Diels-Alder reaction involves a conjugated diene and an alkene, known as the dienophile. The reaction is concerted and occurs via a single, cyclic transition state.
Usually, the diene is electron-rich while the dienophile is electron poor. The HOMO of the diene would interact with the LUMO of the dienophile. However, there is also a possibility of an inverse electron demand Diels-Alder reaction, whereby it is the LUMO of the diene interacting with the HOMO of the dienophile. This can occur if electron withdrawing substituents are added to the diene and electron donating substituents are added to the dienophile. There are other types of Diels-Alder reactions, such as Hetero-Diels-Alder, which involves at least one heteroatom and lewis acid activation Diels-Alder reactions, which involves the use of lewis acids such as zinc chloride to act as catalysts of normal-demand Diels-Alder reactions by coordinating to the dienophile.
When selectivity issues arise, in the case of example 2, where the dienophile is substituted, this would give rise to the possibility of either the endo or exo product. The kinetic endo product is favoured in irreversible reactions due to the stabilisation of the endo transition state by dipolar, orbital and van der waals interactions. The exo product is considered the thermodynamic product due better sterics.
Cheletropic reactions
Cheletropic reactions are pericyclic reactions involving a transition state with a cyclic array of atoms and interacting orbitals. It would involve a reorganisation of sigma and pi bonds in the cyclic array. A key feature of these reactions are that in one of the reagents, both new bonds are being made on the same atom. In the case of example 3, both new bonds are made on the sulfur atom.
Studying Transition States using Gaussview
When more than one product can be formed, it is important to study the transition state. In the formation of kinetic products, the pathway which involves the lower activation energy and hence more stable transition state, is favoured. Should thermodynamic products be favoured, the more stable thermodynamic product is favoured.
Gaussview is being used to study these transition states. By optimising the structures in their transition states, the MOs and their respective energies can be analysed and extracted.
In this lab, semi-empirical PM6 and Density Function Theory (DFT) methods are being used to optimise the structures. PM6 is a faster but less accurate method. It replaces the two electron integrals, exchange and Coulomb integrals, which are challenging to determine.
Nf710 (talk) 21:36, 21 March 2018 (UTC) Some equations would have been nice in this section, but good understanding.
DFT optimisations defines the energy of the system as a summation of 6 individual components, namely: nuclear-nuclear repulsion, nuclear-electron attraction, electron-electron coloumb repulsion, kinetic energy of electrons, electron-electron exchange energies and correlated movement of electrons of different spins.
Nf710 (talk) 21:36, 21 March 2018 (UTC) All quantum chem methods split up the hamiltonian into these parts. DFT is only different because you have the exchange correlation term
Exercise 1: Reaction of Butadiene with Ethylene
(Fv611 (talk) Good job overall.)
Overall reaction scheme
It is to be noted that the trans-butadiene form is the lowest global energy minimum. However, it is the cis conformation that is reacting with ethene.
Molecular orbitals
The three tables below show the jmols of the optimised reactants (butadiene and ethene) as well as MO 16, 17, 18 and 19 of the transition state.
| Butadiene | ||||||||
| Optimised molecule | HOMO | LUMO | ||||||
|---|---|---|---|---|---|---|---|---|
It is to be noted that the trans-butadiene form is the lowest global energy minimum. However, it is the cis conformation that is reacting with ethene.
| Ethene | ||||||||
| Optimised molecule | HOMO | LUMO | ||||||
|---|---|---|---|---|---|---|---|---|
(Fv611 (talk) You added the wrong JMol as an optimised structure (this is not a cope rearrangement).)
| Transition state | ||||||||||||||
| Optimised TS | MO 16 | MO 17 (HOMO) | MO 18 (LUMO) | MO 19 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
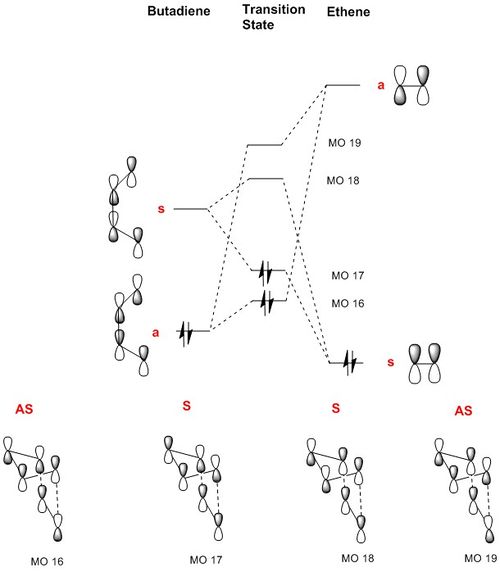
The MO diagram for the transition state is shown below, with S representing 'Symmetric' and AS representing 'Asymmetric'.
It is assumed based on prior knowledge that only orbitals of the same symmetry combine.
It is to be noted that the MO for a TS is very much different compared to a reactant-product MO diagram. For a transition state MO, the resulting orbitals which the electrons occupy are destabilised and at a higher energy level with respect to the original orbitals in the reactants.
The antisymmetric HOMO of butadiene (MO 11) reacts with the antisymmetric LUMO of ethene (MO 7) to give two antisymmetric MOs (MO 16 and 19). Similarly, the symmetric LUMO of butadiene (MO 12) reacts with the symmetric HOMO of ethene (MO 6) to give two symmetric MOs (MO 17 and 18).
When symmetric and asymmetric orbitals overlap, the orbital overlap integral is zero, hence causing them to be unable to overlap, even if they are of similar energies. On the other hand, when two symmetric orbitals or two asymmetric orbitals overlap, the orbital overlap integral is non zero, allowing interaction to occur.
To determine the energy levels of the respective MOs in the TS with respect to the original MOs in butadiene and ethene, the energy levels of the MOs were compared. It was found that MO 16 and 17 were very similar in energy, at -0.32536 and -0.32531 respectively.
Bond lengths
| Butadiene | Ethene | Cyclohexene | Transition state |
|---|---|---|---|
|
|
|
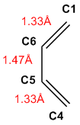
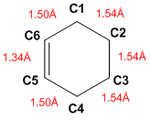
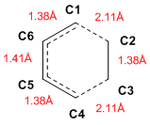
Going from reactants to TS and to products, the shortening of the C5-C6 bond, going from single to double bond was observed. Distances between C1-C2 and C3-C4 were also reduced as bonds were formed. Conversely, lengthening of C1-C6 and C4-C5 bonds were observed, going from double to single bonds.
The typical sp3 and sp2 C-C bond lengths are 1.54 Å and 1.34 Å respectively and the Van der Waals radius of the C atom is 1.70 Å. It can be noted that the partly formed C-C bonds (C1-C2 and C3-C4), which were at lengths 2.11Å in the TS, are longer than the typical sp3 bond, but also shorter than twice the radius of the carbon atom. This would suggest that the orbitals are sufficiently close to interact but the formation of a full C-C bond has yet to be completed.
Reaction pathway
From the jmol file shown below, formation of bonds between diene and dienophile took place simultaneously, hence bond formation is synchronous.
Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole
Molecular orbitals
The jmols of the optimised reactants and products are shown in the tables below. They were optimized using the B3LYP 6-31G(d) level.
| Cyclohexadiene | ||||||||
| Optimised molecule | HOMO | LUMO | ||||||
|---|---|---|---|---|---|---|---|---|
| 1,3 dioxole | ||||||||
| Optimised molecule | HOMO | LUMO | ||||||
|---|---|---|---|---|---|---|---|---|
| Optimised products | |||||
| Exo product | Endo product | ||||
|---|---|---|---|---|---|
At the transition state, the interactions between the 4 MOs (shown above) produced the following 4 MOs for the endo and exo products accordingly.
| Transition State MOs - Exo product | ||||||||||||||
| Optimised molecule | MO 40 | MO 41 (HOMO) | MO 42 (LUMO) | MO 43 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Transition State MOs - Endo product | ||||||||||||||
| Optimised molecule | MO 40 | MO 41 (HOMO) | MO 42 (LUMO) | MO 43 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Based on the energy levels obtained from the log files of the optimised structures, the MO diagram shown below was drawn. For a normal Diels-Alder reaction, where the diene is electron rich and the dienophile is electron poor, the diene has a higher HOMO than the dienophile. However, from the MO diagram in this example, dioxole, which acts as the dienophile, has a higher energy HOMO than cyclohexadiene. This would imply that it is an inverse demand Diels-Alder reaction.
Nf710 (talk) 21:39, 21 March 2018 (UTC) You havent shown that you have done this quantitatively. you have just said that you have have looked at the MOs. You need to look at the reactant MO energies on the same PES (the first step on the irc)
The dienophile is electron rich due to the presence of two oxygen atoms adjacent to the C=C bond, donating electron density to the double bond, hence resulting in a higher energy HOMO.
| Exo | Endo |
|---|---|

|

|
(Fv611 (talk) This is the same MO diagram twice, just with different TS drawn in. You should have shown or discussed the differences between the endo and exo conformations in term of their relative MO energies.)
Calculating Energies
The energies extracted from the log files of the molecules are from optimisations using the B3LYP/6-31G(d) method at 298K.
| Structure | Energy (hartree/particle) |
|---|---|
| Cyclohexadiene | -233.324375 |
| 1,3 dioxole | -267.068132 |
| Endo product | -500.418692 |
| Endo TS | -500.332149 |
| Exo product | -500.417323 |
| Exo TS | -500.329166 |
To calculate the activation and reaction energies for the products formed, the following calculations were made:
1) Activation energy = Energy of TS - sum of energy of reactants
2) Reaction energy = Energy of product - sum of energy of reactants
The conversion between hartree and KJ/mol is: 1 hartree = 2625.4976 KJ/mol
Combined energies of reactants = -1.313779 x 106 KJ/mol
The reaction barriers and reaction energies of the products formed are shown below.
| Activation energies (KJ/mol) | Reaction energies (KJ/mol) | |
|---|---|---|
| Exo | 166.3 | -65.5 |
| Endo | 158.1 | -69.1 |
Kinetic and thermodynamic products
From the calculated reaction energies, it can observed that the endo product is both the kinetic and thermodynamic product. It has a smaller reaction barrier and hence a lower activation energy, making it the kinetic product. Moreover, it also has a lower reaction energy and is more stable than the exo product, hence making it the thermodynamic product.
This is different from the large majority of Diels-Alders reactions, whereby the exo product is more thermodynamically favoured as it has lower steric interactions. The endo product is then the kinetic product due to the presence of stabilising secondary orbital interactions.
The reason for this is as follows. As seen from the 3D chemdraw diagram of the product below, the endo product experiences additional secondary non bonding interactions. It is also slightly less hindered compared to the exo product which experiences a greater steric clash between the two hydrogens (circled in red) which are pointing towards each other in space. The endo product experiences less steric clashes as seen from the fact that the hydrogens are further apart.
Moreover, from the jmols above, the endo TS experiences stabilising secondary orbital interactions between the p orbitals of oxygen in 1,3-dioxole and the p orbitals of carbon in cyclohexadiene. These interactions are not present in the exo product. Hence the TS of the endo product would be lower in energy.
Nf710 (talk) 21:42, 21 March 2018 (UTC) Your energies are correct and you have come to the correct conclusions. you could have gone into some more detail in certain areas. The diagram of sterics is really nice.
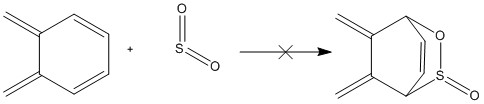
Exercise 3: Diels-Alder vs Cheletropic
Unlike the previous two examples, which are purely Diels-Alder reactions, this final example involves a competing cheletropic reaction in addition to the Diels-Alder reaction pathways.
It is common for cheletropic reactions to involve SO2. Such a competing reaction arises due to the competing thermodynamic and kinetic products. Experimental work has found that Diels-Alder product is the kinetic product of SO2 with conjugated dienes. However, this product is thermally unstable and undergoes a retro-Diels-Alder reaction. A thermodynamic product then forms, producing a stable five membered ring. Hence, the dominance of cheletropic products arises not from reactivity but from product instability. [1]
The optimised structures of the reactants, transition states and products that have been optimized at PM6 level of the 3 different reaction routes are shown below:
| Optimised structures at 298K | |||||||||||||||||||||||
| Xylylene | SO2 | Endo TS | Exo TS | Cheletropic TS | Endo Product | Exo Product | Cheletropic Product | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
(It seems that you've read in the wrong file for the Endo TS (it has frozen bonds). It's also missing 2 hydrogens. For all your JMols you must make sure you select the correct frame Tam10 (talk) 13:28, 16 March 2018 (UTC))
IRC paths
The IRC paths for these 3 reactions as well as the log file links are shown below.
| Endo DA reaction | 
|
File:CJC415 Ex3 ENDO PRODUCT.LOG |
| Exo DA reaction | 
|
File:CJC415 Ex3 EXO PRODUCT.LOG |
| Cheletropic reaction | 
|
File:CJC415 Ex3 CHELETROPIC PRODUCT.LOG |
Energy calculations
The optimized energies of the structures in hartrees obtained from their log files are tabulated below.
| Structure | Energy at RT (hartree/particle) |
|---|---|
| Xylylene | 0.178764 |
| SO2 | -0.118614 |
| Exo DA TS | 0.092077 |
| Exo DA Product | 0.021451 |
| Endo DA TS | 0.090559 |
| Endo DA Product | 0.021697 |
| Cheletropic TS | 0.099062 |
| Cheletropic Product | 0.000005 |
(Your xylylene energy is a bit high Tam10 (talk) 13:28, 16 March 2018 (UTC))
Similar as the previous calculations:
1) Activation energy = Energy of TS - sum of energy of reactants
2) Reaction energy = Energy of product - sum of energy of reactants
The conversion between hartree and KJ/mol is: 1 hartree = 2625.4976 KJ/mol
Combined energies of reactants = 157.9236 KJ/mol
| Activation energies (KJ/mol) | Reaction energies (KJ/mol) | |
|---|---|---|
| Exo DA | 83.8 | -101.6 |
| Endo DA | 79.8 | -100.9 |
| Cheletropic | 102.2 | -157.9 |
Using the values calculated from above, the following reaction coordinate was drawn.
(Please use straight lines for reaction profiles. But the data is clear Tam10 (talk) 13:28, 16 March 2018 (UTC))
From the reaction profile and calculations above, it can be seen that the activation energy of both endo and exo reactions are similar in energy, at +79.8KJ/mol and +83.8KJ/mol respectively. It is much lower than the cheletropic reaction which has an activation of +102.2KJ/mol. This is because both the transition states of the endo and exo pathways experience stabilising secondary interactions while the cheletropic TS, which also has numerous nodes, does not.
(Numerous nodes in the HOMO? It would be good to show this Tam10 (talk) 13:28, 16 March 2018 (UTC))
It can be easily seen that the thermodynamic product is the cheletropic product due to the fact that the product is of the lowest energy. However, the amount of activation energy required is the largest. Hence, this pathway is likely to be reactive only under thermodynamic conditions, such as at high temperature and under equilibrating conditions.
Favouring the cheletropic product which is the most stable could be because the product is able to adopt a planar geometry, allowing the distance between the oxygen and neighbouring hydrogen atoms to be maximised.
Based on the activation energy values, it can be deduced that the endo Diels-Alders product is the kinetic product as that reaction pathway has the lowest energy barrier. This is because the endo product has secondary stabilising interactions between the oxygen on sulfur dioxide and the pi system of xylylene. Hence, this route would be favoured when the reaction is irreversible, under low temperatures and non equilibrating conditions.
Extension: Reaction at second cis-butadiene fragment of xylylene
One of the key reasons why the cheletropic and Diels-Alders reactions occur (shown above) is due to the reactivity of xylylene. Though it has a conjugated pi system and is planar, it is not aromatic. This is because the π electrons are not in a cyclic arrangement and since xylylene contains 8 π electrons, it does not fulfill Hückel's rule which states that a cyclic, planar molecule with 4n+2 π electrons are required for the molecule to be aromatic. Hence, xylylene is anti-aromatic. The formation of a stable aromatic benzene ring in the above 3 reactions would drive product formation, since the products are more stable than the reactants.
Apart from the outer cis-butadiene, there is another inner cis-butadiene fragment present that can participate in a Diels-Alders reaction. However, this site is not favoured due to the presence of steric hinderance and the formation of a strained bicyclic ring in the product as shown in the reaction scheme below.
It is important to note that in the cheletropic and Diels-Alders reactions involving the outer cis-butadiene, a stable benzene ring is formed in the product. However, this stabilising aromaticity is not found when the inner cis-butadiene reacts, causing it to be unfavoured.
| Log file | Energy (hartress) | |
|---|---|---|
| Exo TS | File:CJC415 Extension EXO TS.LOG | 0.105054 |
| Exo Product | File:CJC415 Extension EXO PRODUCT.LOG | 0.067301 |
| Endo TS | File:CJC415 Extension ENDO TS.LOG | 0.102070 |
| Endo Product | File:CJC415 Extension ENDO PRODUCT.LOG | 0.065607 |
Similar to the previous section, the combined energies of reactants = 157.9236 KJ/mol. Hence, using the same formulas to calculate the activation and reaction energies, the following values were obtained:
| Activation energies (KJ/mol) | Reaction energies (KJ/mol) | |
|---|---|---|
| Exo DA | 117.9 | 18.8 |
| Endo DA | 110.1 | 14.3 |
Conclusion
Different pericyclic reactions were studied in this lab using Gaussian to optimize the products, reactants and transition states as well as study their optimized geometry. This has allowed us to rationalize and explain the reasoning behind why certain products were favoured over others as well as calculate the activation and reaction energies of these pathways. Doing so has allowed us to draw out the MOs to see the orbital interactions as well as predict product formation, something extremely useful that can be done before experiments are being carried out.