Rep:Mod:cinnamonroll
BH3
Using GaussView 5.0, BH3 was modelled, setting bond lengths to 1.5 Å. The structure was then optimised with the DFT/B3LYP method and 3-21G basis set. The resulting structure (Fig. 1) is a trigonal planar molecule of D3h symmetry, bond angles of 120.0° and a B-H bond distance of 1.19 Å.

The output file of the optimisation was checked to see the forces and displacements had converged.

Item Value Threshold Converged? Maximum Force 0.000413 0.000450 YES RMS Force 0.000271 0.000300 YES Maximum Displacement 0.001610 0.001800 YES RMS Displacement 0.001054 0.001200 YES Predicted change in Energy=-1.071764D-06 Optimization completed.
The results summary shows that the gradient is near zero. The gradient represents the first derivative of the molecule's potential energy surface, so a zero result confirms that the structure's energy is a minimum. From the energy and gradient graphs (Fig. 3 and Fig. 4), we see that the calculation converged in four steps.
 |
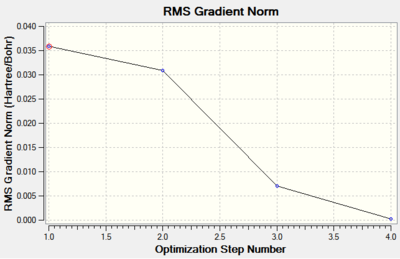 |
|---|---|
| Figure 3: Changes in energy during the optimisation. | Figure 4: Changes in gradient during the optimisation. |
Frequency analysis
Frequency analysis was carried out on the optimised structure using the same method and basis set. As the vibrational frequency represents the second derivative of the potential energy surface, all positive frequencies confirm that the optimised structure is a minimum (as opposed to e.g. a transition state, causing some frequencies to be negative).

We see that there are six distinct vibrational modes (Table 1), but only three are observed in the actual spectrum (Fig. 5). The vibration at 2598 cm-1 is completely symmetrical. This creates no dipole change, rendering the vibration IR inactive. The observed peak at 1204 cm-1 is in fact due to two degenerate vibrational modes (both E'), as is the case for the peak observed at 2737 cm-1.
| Vibrational mode | Frequency (cm-1) | Intensity | Symmetry point group |
|---|---|---|---|
| 1 | 1144 | 93 | A2" |
| 2 | 1204 | 12 | E' |
| 3 | 1204 | 12 | E' |
| 4 | 2598 | 0 | A1' |
| 5 | 2737 | 104 | E' |
| 6 | 2737 | 104 | E' |
COMPARE FREQUENCIES TO LITERATURE
MO analysis
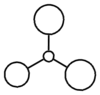
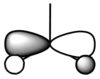
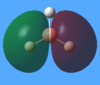
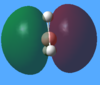
The MO diagram of BH3 was constructed using the LCAO approach (Fig. 6). The 1s orbital of boron was too low in energy to interact with the hydrogen orbitals. The relative energies of the H fragment orbitals and the B atomic orbitals were based on the electronegativity difference (hydrogen is more electronegative than boron by 0.16 on the Pauling scale).

Energy analysis of the optimised BH3 was carried out with the DFT/B3LYP method and 3-21G basis set on the HPC server (http://hdl.handle.net/10042/to-10529). The first eight molecular orbitals were visualised and compared with those predicted in the diagram (Table 2).
| MO-1 | MO-2 | MO-3 | MO-4 | MO-5 | MO-6 | MO-7 | MO-8 |
|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
The predicted ordering of the resulting MO's corresponds to the computed one. The shapes of the molecular orbitals are also very similar, although MO's 6 and 7 are relatively difficult to compare. The correct ordering and similarity in shapes highlights the usefulness of MO diagrams as a relatively simple qualitative approach to rationalising bonding and reactivity in molecules.
NBO analysis and charge distribution

The charge distribution of the molecule was visualised (Fig. 7), with green representing positive charge and red representing negative charge. The boron centre is seen to be positive, which reflects its electron deficiency and Lewis acidic nature. The symmetrical arrangement of the negative charge around the positive charge reflects the lack of dipole moment (the otimisation results summary gave a dipole moment of 0.0 Debye). The relative charges of the atoms are 0.33 for boron and -0.11 for each of the hydrogens.
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
B 1 0.33161 1.99903 2.66935 0.00000 4.66839
H 2 -0.11054 0.00000 1.11021 0.00032 1.11054
H 3 -0.11054 0.00000 1.11021 0.00032 1.11054
H 4 -0.11054 0.00000 1.11021 0.00032 1.11054
=======================================================================
* Total * 0.00000 1.99903 6.00000 0.00097 8.00000
In order to consider the NBO's more closely, the output file was investigated further. We see that the first NBO consists 45.5.% of boron's orbitals, which in turn are 33.3% s and 66.7% p. This corresponds to an sp2 orbital. The hydrogen 1s orbitals contribute 55.5% to the NBO.
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.99853) BD ( 1) B 1 - H 2
( 44.48%) 0.6669* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.0000 0.0000
0.8165 0.0000 0.0000 0.0000
( 55.52%) 0.7451* H 2 s(100.00%)
1.0000 0.0000
2. (1.99853) BD ( 1) B 1 - H 3
( 44.48%) 0.6669* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 55.52%) 0.7451* H 3 s(100.00%)
1.0000 0.0000
3. (1.99853) BD ( 1) B 1 - H 4
( 44.48%) 0.6669* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 -0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 55.52%) 0.7451* H 4 s(100.00%)
1.0000 0.0000
4. (1.99903) CR ( 1) B 1 s(100.00%)
1.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000
5. (0.00000) LP*( 1) B 1 s(100.00%)
The fifth NBO consists of the lone pair of boron. According to the NBO analysis, the lone pair is shown to be 100.0% s, which disagrees with the traditional idea of a p-character lone pair. This was thought to be due to the low level accuracy of the 3-21G basis set, so the energy analysis was repeated with the higher 6-31G basis set (http://hdl.handle.net/10042/to-10590), but the NBO analysis (see below) still showed the lone pair to be 100.0% s. The discrepancy is most likely due to the relatively inaccurate modelling of lone pairs by Gaussian.
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.99856) BD ( 1) B 1 - H 2
( 45.36%) 0.6735* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.0000 0.0000
0.8165 0.0000 0.0000 0.0000
( 54.64%) 0.7392* H 2 s(100.00%)
1.0000 0.0001
2. (1.99856) BD ( 1) B 1 - H 3
( 45.36%) 0.6735* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 54.64%) 0.7392* H 3 s(100.00%)
1.0000 0.0001
3. (1.99856) BD ( 1) B 1 - H 4
( 45.36%) 0.6735* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 -0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 54.64%) 0.7392* H 4 s(100.00%)
1.0000 0.0001
4. (1.99954) CR ( 1) B 1 s(100.00%)
1.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000
5. (0.00000) LP*( 1) B 1 s(100.00%)
The Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis showed no mixing of MO's. This is as predicted due to the high symmetry of BH3.
TlBr3
The structure of TlBr3 was optimised using the B3LYP method and LANL2DZ basis set (.log file), and the convergence checked.

Item Value Threshold Converged? Maximum Force 0.000002 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000022 0.001800 YES RMS Displacement 0.000014 0.001200 YES Predicted change in Energy=-6.082801D-11 Optimization completed.
The optimised structure was trigonal planar with D3h symmetry, a Tl-Br bond distance of 2.65 Å and a bond angle of 120.0°. These are very similar to those calculated previously for TlF3 (2.55 Å and 120.0°[1]).

Frequency analysis was carried out with the B3LYP method and LANL2DZ basis set. All frequencies were positive, and the structure was confirmed as a minimum (similar to the treatment of BH3). The same method and basis set were used for both the structural optimisation and frequency analysis, as the use of different methods would effectively result in different calculations and make comparison of the two results useless.

The real output file was checked for the low frequencies. They were all below 5 cm-1. The lowest "real" normal mode occurred at 46 cm-1, which is an order of magnitude greater than the highest low frequency. This suggests the relative movement of the centre of mass is low, and the accuracy of the predicted real frequencies is good.
Low frequencies --- -3.4213 -0.0026 -0.0004 0.0015 3.9367 3.9367 Low frequencies --- 46.4289 46.4292 52.1449
The predicted IR spectrum is shown in Figure 11 and the vibrational frequencies have been listed in Table 3.

| Vibrational mode | Frequency (cm-1) | Intensity | Symmetry point group |
|---|---|---|---|
| 1 | 46 | 4 | E' |
| 2 | 46 | 4 | E' |
| 3 | 52 | 6 | A2" |
| 4 | 165 | 0 | A1' |
| 5 | 211 | 25 | E' |
| 6 | 211 | 25 | E' |
There are six distinct vibrational modes, but only three are observed. The fourth mode (at 165 cm-1) is completely symmetrical with no resulting dipole moment, rendering it IR inactive (as reflected in the fact that it has 0 intensity). The first and second vibrations at 46 cm-1 are degenerate, resulting in only one observable peak, which overlaps with the peak from the third vibrational mode. The fifth and sixth vibrations at 211 cm-1 are also degenerate, resulting in one observable peak.
Isomers of Mo(CO)4L2
Mo(CO)4(PPh3)2 was studied in the second year synthesis lab course, and the spectral differences between the cis- and trans-isomers dicussed. The trans-isomer exhibits only one C=O stretch in its IR spectrum, whereas the cis-isomer exhibits four peaks. In order to further investigate the reasons behind this, Mo(CO)4(PPh3)2 was modelled, however as the Ph groups are very large, they were replaced with chlorines.
Optimisation with B3LYP method and LANL2MB basis set
Both structures were optimised on the HPC server using the above-defined method and basis set(trans-isomer:, cis-isomer:http://hdl.handle.net/10042/to-10598).
The convergence of the files was checked.
Item Value Threshold Converged? Maximum Force 0.000186 0.002500 YES RMS Force 0.000056 0.001667 YES Maximum Displacement 0.003674 0.010000 YES RMS Displacement 0.001015 0.006667 YES Predicted change in Energy=-6.617297D-07 Optimization completed.

Item Value Threshold Converged? Maximum Force 0.000714 0.002500 YES RMS Force 0.000192 0.001667 YES Maximum Displacement 0.009868 0.010000 YES RMS Displacement 0.003500 0.006667 YES Predicted change in Energy=-4.775265D-06 Optimization completed.
 |
 |
|---|---|
| trans-Mo(CO)4(PCl3)2 | cis-Mo(CO)4(PCl3)2 |
The actual optimised structures do not include P-Cl bonds when represented on GaussView. This does not mean that there is no bond between the two atoms, as the line connecting them is not an accurate representation of what actually constitutes a bond. A bond is generally considered to be a region of electron density, shared between two or more valence orbitals of atomic centres. The centres must be close enough to have an attractive interaction, but sometimes this distance may be too long for GaussView to recognise. The bonds have been drawn in manually, as has been done with most of the following molecules to represent the expected, traditional connections between atoms within the molecule.
Optimisation with B3LYP method and LANL2DZ basis set
The torsion angle on the PCl3 groups was altered to make the groups eclipsed on the trans-isomer (with one P-Cl bond aligned with an Mo-C bond), and staggered on the cis-isomer (with one P-Cl bond on each group aligned with a Mo-C bond). The structures were then optimised further with the more accurate LANL2DZ basis set (trans-isomer:http://hdl.handle.net/10042/to-10597, cis-isomer:http://hdl.handle.net/10042/to-10596). The convergence was checked.
Item Value Threshold Converged? Maximum Force 0.000040 0.000450 YES RMS Force 0.000009 0.000300 YES Maximum Displacement 0.000858 0.001800 YES RMS Displacement 0.000230 0.001200 YES Predicted change in Energy=-1.477114D-08 Optimization completed.

Item Value Threshold Converged? Maximum Force 0.000030 0.000450 YES RMS Force 0.000008 0.000300 YES Maximum Displacement 0.001318 0.001800 YES RMS Displacement 0.000416 0.001200 YES Predicted change in Energy=-2.122906D-08 Optimization completed.
 |
 |
|---|---|
| trans-Mo(CO)4(PCl3)2 | cis-Mo(CO)4(PCl3)2 |
Comparing the optimised structures, the cis-isomer has a lower energy by about 8 kJ mol-1 using the LANL2MB basis set, and 3 kJ mol-1 using the LANL2DZ basis set. These are very small energy differences, and considering the accuracy of the calculations, the relative energy difference between the isomers actually falls within error (10 kJ mol-1). The relative stability of the isomers could be altered by e.g. changing the chlorines for smaller atoms (reducing steric bulk) or carboxylic acids (increasing attractive H-bonding within the PR3 ligand).
Frequency analysis with B3LYP method and LANL2DZ basis set
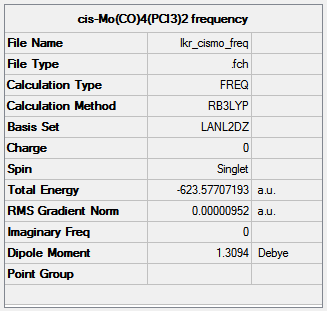
Frequency analysis was carried out on the optimised structures using the same method and basis set to ensure reliable comparison of the results (trans-isomer:http://hdl.handle.net/10042/to-10595, cis-isomer:http://hdl.handle.net/10042/to-10594). All the vibrational frequencies were positive, confirming that the optimised structures were indeed minima.
 |
|
|---|
The predicted spectra are shown below, with a close-up of the C=O stretching region of the cis-isomer.
 |
 |
 |
|---|---|---|
| IR spectrum for trans-Mo(CO)4(PCl3)2 | IR spectrum for cis-Mo(CO)4(PCl3)2 | C=O region of cis-Mo(CO)4(PCl3)2 |
Similar to the experimental results in the second year lab course, the trans-isomer displays one C=O peak around 1950 cm-1, although on closer inspection it turns out to two peaks at almost identical frequencies due to a pair of almost degenerate eu vibrational modes. The third and fourth vibrational modes (of b1g and a1g symmetry) are IR inactive.
| Vibrational mode | Frequency (cm-1) | Intensity | Symmetry point group |
|---|---|---|---|
| 1 | 1950 | 1475 | Eu |
| 2 | 1951 | 1467 | Eu |
| 3 | 1977 | 1 | B1g |
| 4 | 2031 | 4 | A1g |
The IR spectrum of the cis-isomer displays four distinct C=O peaks, as predicted.
| Vibrational mode | Frequency (cm-1) | Intensity | Symmetry point group |
|---|---|---|---|
| 1 | 1945 | 763 | B2' |
| 2 | 1949 | 1499 | B2" |
| 3 | 1958 | 633 | A1' |
| 4 | 2023 | 598 | A1' |
Some very low frequencies were also observed in the spectra, and have been summarised in the table below. These have very low intensity and low energies. The stretching modes are due to various movements in the PCl3 groups and their heavy nature results in the low energy. At room temperature, the energy of the surroundings is greater than that of the vibrations, so there is enough energy for free rotation to occur.
| Frequency (cm-1) (trans) | Intensity | Frequency (cm-1) (cis) | Intensity |
|---|---|---|---|
| 5 | 0.1 | 11 | 0.0 |
| 6 | 0.0 | 18 | 0.0 |
| 37 | 0.4 | 42 | 0.1 |
| 40 | 0.3 |
Interestingly the cis-isomer shows two different Mo-C bond lengths: the Mo-C bonds that are perpendicular to the PCl3 groups have an optimised bond distance of 2.06 Å (similar to the Mo-C bonds in the trans-isomer), while the Mo-C bonds in the same plane as the PCl3 groups are shorter at 2.01 Å. The shortening of the bonds is due to the trans-effect of the PCl3 groups, slightly increasing the energy of these Mo-C bonds.
The bond angles around the Mo centre were all close to 90°, with slight deviations most likely due to the bulkiness of the PCl3 groups (pushing the C=O groups 'away' to a smaller angle) or small Cl-P-Mo-C dihedral angles.
Mini-Project
Boranes have enjoyed great interest due to their ability to form interesting deltahedral clusters. Bonding in these clusters has been rationalised by Skeletal Electron pair (SEP) Theory, originally introduced by K. Wade in the 1970s[2].
The focus of this project is on the B3H8- anion met in the third year inorganic synthesis lab course. Based on Wade's rules, the anion is predicted to have an arachno-structure with three boron vertices. The aim of this project is to investigate the structure of the anion and compare the results of a computational modelling method to those obtained experimentally. The changes in bonding and charge distribution, on substitution of aluminium for boron are also investigated. Vibrational frequencies are predicted for the anion and compared to literature and those obtained in the lab course.
Structural optimisation with the B3LYP method and LANL2MB basis set
The structure of (B3H8)- was optimised using the DFT/B3LYP method and the low level LANL2MB basis set to obtain a relatively good starting structure. The convergence of forces and displacement was checked in the real output file.


Item Value Threshold Converged? Maximum Force 0.000034 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.000724 0.001800 YES RMS Displacement 0.000204 0.001200 YES Predicted change in Energy=-1.029481D-08 Optimization completed.
(B2AlH8)-, (BAl2H8)- and (Al3H8)-
Optimisations were carried out on (B2AlH8)-, (BAl2H8)- and (Al3H8)- using the same method and basis set. Convergence was checked for all from the real output file. Frequency analysis was carried out to confirm the resulting structures were minima.
| Compound | (B2AlH8)- | (BAl2H8)- | (Al3H8)- |
|---|---|---|---|
| Optimisation results summary |  |
 |
 |
| D-space link | http://hdl.handle.net/10042/to-10936 | http://hdl.handle.net/10042/to-10939 | http://hdl.handle.net/10042/to-10941 |
| Frequency results summary |  |
 |
 |
| D-space link | http://hdl.handle.net/10042/to-10929 | http://hdl.handle.net/10042/to-10928 | http://hdl.handle.net/10042/to-10927 |
Convergence of the optimisation of (B2AlH8)-.
Item Value Threshold Converged? Maximum Force 0.000066 0.000450 YES RMS Force 0.000013 0.000300 YES Maximum Displacement 0.001355 0.001800 YES RMS Displacement 0.000405 0.001200 YES Predicted change in Energy=-5.181098D-08 Optimization completed.
Convergence of the optimisation of (BAl2H8)-.
Item Value Threshold Converged? Maximum Force 0.000029 0.000450 YES RMS Force 0.000008 0.000300 YES Maximum Displacement 0.000908 0.001800 YES RMS Displacement 0.000282 0.001200 YES Predicted change in Energy=-2.231730D-08 Optimization completed.
Convergence of the optimisation of (Al3H8)-.
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000002 0.000300 YES Maximum Displacement 0.000375 0.001800 YES RMS Displacement 0.000126 0.001200 YES Predicted change in Energy=-2.004936D-09 Optimization completed.
The resulting structures are listed below. There is a visible change in bond angle in the B-H-B bridge on the introduction of aluminium to the system. All optimised structures have C2v symmetry, which agrees with literature[3][4].
Structural optimisation with the B3LYP method and 6-311G(d,p) basis set
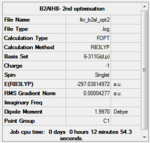
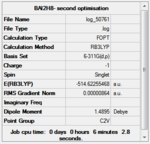
The structures were then further optimised using the DFT/B3LYP method and a higher level 6-311G9(d,p) basis set.
The convergence of all jobs was checked in the real output file (see below), and a frequency analysis was carried out with the same method and basis set.
| Compound | (B3H8)- | (B2AlH8)- | (BAl2H8)- | (Al3H8)- |
|---|---|---|---|---|
| Optimisation results summary | 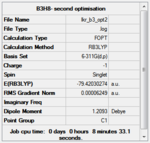 |
 |
 |
 |
| D-space link | http://hdl.handle.net/10042/to-10933 | http://hdl.handle.net/10042/to-10932 | http://hdl.handle.net/10042/to-10931 | http://hdl.handle.net/10042/to-10934 |
| Frequency results summary |  |
 |
 |
 |
| D-space link | http://hdl.handle.net/10042/to-10926 | http://hdl.handle.net/10042/to-10925 | http://hdl.handle.net/10042/to-10924 | http://hdl.handle.net/10042/to-10923 |
The resulting optimised structures are shown below. They are very similar to those obtained with the LANL2MB basis set, with some increase in symmetry.
Convergence of (B3H8)-
Item Value Threshold Converged? Maximum Force 0.000105 0.000450 YES RMS Force 0.000025 0.000300 YES Maximum Displacement 0.001087 0.001800 YES RMS Displacement 0.000219 0.001200 YES Predicted change in Energy=-1.745487D-07 Optimization completed.
Convergence of (B2AlH8)-
Item Value Threshold Converged? Maximum Force 0.000097 0.000450 YES RMS Force 0.000032 0.000300 YES Maximum Displacement 0.001287 0.001800 YES RMS Displacement 0.000500 0.001200 YES Predicted change in Energy=-2.523344D-07 Optimization completed.
One negative frequency at -146 cm-1. On inspection of the real output file, it was noted that the forces had converged (see below).
Item Value Threshold Converged? Maximum Force 0.000121 0.000450 YES RMS Force 0.000061 0.000300 YES Maximum Displacement 0.017273 0.001800 NO RMS Displacement 0.007149 0.001200 NO
Convergence of (BAl2H8)-
Item Value Threshold Converged? Maximum Force 0.000061 0.000450 YES RMS Force 0.000018 0.000300 YES Maximum Displacement 0.000224 0.001800 YES RMS Displacement 0.000083 0.001200 YES Predicted change in Energy=-9.464318D-09 Optimization completed.
One negative frequency was observed at 152 cm-1, however on inspecting the real output file of the frequency analysis, the calculations had converged (See below).
Item Value Threshold Converged? Maximum Force 0.000059 0.000450 YES RMS Force 0.000025 0.000300 YES Maximum Displacement 0.000201 0.001800 YES RMS Displacement 0.000083 0.001200 YES Predicted change in Energy=-1.108116D-08 Optimization completed.
Convergence of (Al3H8)-
Item Value Threshold Converged? Maximum Force 0.000369 0.000450 YES RMS Force 0.000107 0.000300 YES Maximum Displacement 0.001450 0.001800 YES RMS Displacement 0.000689 0.001200 YES Predicted change in Energy=-2.278662D-07 Optimization completed.
Structural analysis
Selected bond length in the (B3H8)- molecule have been listed below and compared with those reported in literature. Literature values in brackets were obtained through computational chemistry (MP2 method and expanded STO 3-21G basis set). Agreement is very good.

| Bond | Length (Å) | Length (lit.[5], Å) |
|---|---|---|
| B1-B2 | 1.80 | 1.77 (1.81) |
| B2-B3 | 1.83 | 1.80 (1.92) |
| B1-H1 | 1.50 | 1.5 (1.58) |
| H1-B2 | 1.36 | 1.2 (1.26) |
Frequency analysis with the B3LYP method and 6-311G(d,p) basis set
Frequency analysis was carried out using the same method and basis set as for the optimisation. Predicted IR spectra are shown below, together with key vibrational modes from the spectrum of (B3H8)-.
 |
 |
 |
 |
|---|---|---|---|
| (B3H8)- | (B2AlH8)- | (BAl2H8)- | (Al3H8)- |
| Frequency (cm-1) | Experimental (cm-1) | Functional group |
|---|---|---|
| 1035 | 1009 | BH2 |
| 1159 | 1138 | BB |
| 2167 | 2065 | B-H-B |
| 2212 | 2115 | B-H-B |
| 2443 | 2384 | BH2 |
| 2452 | 2436 | BH2 |
All the experimentally observed frequencies are present in the predicted spectrum, but there are quite large differences in frequencies. This may be due to the different environment of the experimentally recorded spectrum, but the predicted spectrum can be of use in helping the analysis of the experimental spectrum.
MO analysis
Energy analysis was done with the DFT/B3LYP method and 6-311G(d,p) basis set (http://hdl.handle.net/10042/to-10917). All the occupied MO's were visualised. The MO diagram proved to be too difficult to predict in the time available, but it would be interesting to compare the predicted MO's with those computed. The HOMO and LUMO are relatively complex, reflecting the unusual bonding in the borohydrate.
| MO-1 | MO-2 | MO-3 | MO-4 | MO-5 | MO-6 | MO-7 | MO-8 | Mo-9 | MO-10 | MO-11 | MO-12 (HOMO) | MO-13 (LUMO) | MO-14 (LUMO+1) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
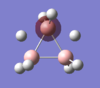 |
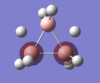 |
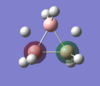 |
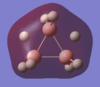 |
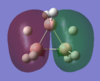 |
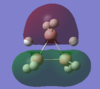 |
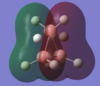 |
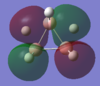 |
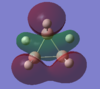 |
 |
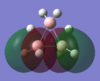 |
 |
 |
 |
NBO analysis
The charge distribution of (B3H8)- was visualised (Fig. X). As predicted, the whole molecule is negatively charged due to its anionic nature. The bridging hydrogens almost black, suggesting they are more or less neutral. This is due to the reduced electron density that is characteristic of 3 centre-2 electron bonds (there are "only 0.89 electrons on the bridging hydrogens). The neutral nature of the bridging hydrogens is also seen in the Summary of Natural Population Analysis (see below), as H2 and H4 are the only atoms with a non-negative natural charge.

Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
B 1 -0.42006 1.99900 3.41353 0.00753 5.42006
H 2 0.10560 0.00000 0.88907 0.00533 0.89440
B 3 -0.42006 1.99900 3.41353 0.00753 5.42006
H 4 0.10560 0.00000 0.88907 0.00533 0.89440
B 5 -0.19772 1.99877 3.19179 0.00715 5.19772
H 6 -0.03809 0.00000 1.03565 0.00243 1.03809
H 7 -0.03809 0.00000 1.03565 0.00243 1.03809
H 8 -0.02430 0.00000 1.02221 0.00209 1.02430
H 9 -0.02430 0.00000 1.02221 0.00209 1.02430
H 10 -0.02430 0.00000 1.02221 0.00209 1.02430
H 11 -0.02430 0.00000 1.02221 0.00209 1.02430
=======================================================================
* Total * -1.00000 5.99677 17.95715 0.04608 24.00000
Comparing the borons, we see that the boron located at the "top" vertex is darker in colour, and indeed has a smaller negative charge compared to the other borons (B(5) has a natural charge of -1.98 compared to -0.42 on B(1) and B(3) in the Summary above). This, and the bridging hydrogens demonstrate the resulting dipole in the molecule (1.2 Debye as according to the results summary of the optimisation).
On substitution of the "top" boron for aluminium, a positively charged centre is introduced. The aluminium atom is highly positive, the bridging hydrogens now carry a negative charge (although still very small at -0.1) and the terminal BH2 hydrogens ((H7), H(8), H(9) and H(10)) have been rendered less negative.

Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
B 1 -0.60350 1.99898 3.59615 0.00837 5.60350
H 2 -0.04279 0.00000 1.03848 0.00431 1.04279
B 3 -0.60428 1.99898 3.59692 0.00838 5.60428
H 4 -0.04257 0.00000 1.03826 0.00431 1.04257
H 5 -0.36522 0.00000 1.36296 0.00226 1.36522
H 6 -0.36524 0.00000 1.36298 0.00226 1.36524
H 7 -0.01055 0.00000 1.00887 0.00168 1.01055
H 8 -0.00976 0.00000 1.00809 0.00167 1.00976
H 9 -0.00984 0.00000 1.00817 0.00167 1.00984
H 10 -0.01066 0.00000 1.00898 0.00168 1.01066
Al 11 1.06440 9.99713 1.91556 0.02291 11.93560
=======================================================================
* Total * -1.00000 13.99509 17.94542 0.05949 32.00000
Similarly for (BAl2H8)- the aluminiums carry a positive natural charge.

Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
H 1 -0.36250 0.00000 1.35997 0.00253 1.36250
H 2 -0.11573 0.00000 1.11301 0.00272 1.11573
H 3 -0.36250 0.00000 1.35997 0.00253 1.36250
H 4 -0.36250 0.00000 1.35997 0.00253 1.36250
H 5 -0.11573 0.00000 1.11301 0.00272 1.11573
H 6 -0.36250 0.00000 1.35997 0.00253 1.36250
H 7 -0.02866 0.00000 1.02708 0.00158 1.02866
H 8 -0.02866 0.00000 1.02708 0.00158 1.02866
Al 9 0.54161 9.99757 2.44353 0.01729 12.45839
Al 10 0.54161 9.99757 2.44353 0.01729 12.45839
B 11 -0.34446 1.99922 3.33975 0.00549 5.34446
=======================================================================
* Total * -1.00000 21.99435 17.94686 0.05879 40.00000
Interestingly, when all borons have been substituted for aluminium atoms, there is little difference in the natural charge of the hydrogens.

Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
H 1 -0.34533 0.00000 1.34291 0.00242 1.34533
H 2 -0.34794 0.00000 1.34420 0.00374 1.34794
H 3 -0.34533 0.00000 1.34291 0.00242 1.34533
H 4 -0.34533 0.00000 1.34291 0.00242 1.34533
H 5 -0.34794 0.00000 1.34420 0.00374 1.34794
H 6 -0.34533 0.00000 1.34291 0.00242 1.34533
H 7 -0.35082 0.00000 1.34860 0.00222 1.35082
H 8 -0.35082 0.00000 1.34860 0.00222 1.35082
Al 9 0.90087 9.99864 2.08318 0.01731 12.09913
Al 10 0.43899 9.99808 2.54564 0.01729 12.56101
Al 11 0.43899 9.99808 2.54564 0.01729 12.56101
=======================================================================
* Total * -1.00000 29.99481 17.93171 0.07348 48.00000
Conclusions
The bond lengths and general structure of the (B3H8)- ion were modelled succesfully, suggesting the methods and basis sets used were sufficiently accurate. The predicted IR spectrum exhibited all the expected vibrational frequencies, although at slightly higher frequencies. Comparison of the charge distribution and NBO analysis of the ion and its Al-substituted derivatives provided interesting results. Further investigation on the less symmetrical substituted anions (i.e. a single Al or B at one of the bottom vertices) could prove interesting.
- ↑ M. Atanasov, D. Reinen, J. Phys. Chem. A, 2001, 105, 5467 DOI:10.1021/jp004511j
- ↑ K. Wade, Adv. Inorg. Chem. Radiochem., 1976, 18
- ↑ M. Sironi, M. Raimondi, D. L. Cooper, J. Gerratt, J. Phys. Chem., 1991, 95, 10617DOI:10.1021/j100179a024
- ↑ C. Serrar, A. Es-sofi A. Boutalib, A. Ouassas, A. Jarid, J. Mol. Struct. (Theochem), 1999, 491, 161DOI:10.1016/S0166-1280(99)00103-7
- ↑ M. Sironi, M. Raimondi, D. L. Cooper, J. Gerratt, J. Phys. Chem., 1991, 95, 10617DOI:10.1021/j100179a024








