Jump to content

Rep:Mod:chilong module3

From ChemWiki

by Chi Long Chan


Cope

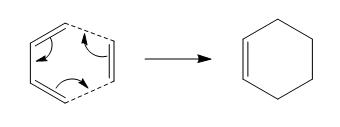
The isomerization of 1,5 diene has always been a popular topic for researcher ever since its discovery in 1940 by Arthur C. Cope [1]. It has many variations and uses in organic synthesis. It can be very useful in functional group interconvertions, for example as Oxy-Cope rearrangement (with OH group at C3 position, which after rearrangment becomes enol) or Aza-Cope rearrangement (involving heteroatom) etc[2]. This reaction can take place in two possible Transition States: Chair and Boat, and in this project, we will be using computational analysis to investigate which is the more likely transition state.

Reactants: 1,5 hexadiene

Optimization with Hartree Fock

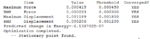
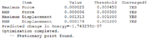
At first, a number of possible conformers of the reactant (1,5 hexadiene) were drawn using gaussview. Theses structures were then optimized at HF/3-21G level theory ( Hartree Fock as method,3-21G as basis set), in order to obtain relevant information of them. The results of the optimization is summarized in below table:

HF Optimized structures
Conformer Structures Point groups Energy in Hartrees Relative Energy in kcal/mol Optimization summary
anti 1[3]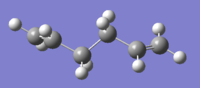
C2 -231.69260 0.04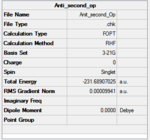
First optimized Anti-structure
anti 3[4]
C2h -231.68907 2.25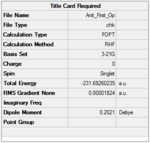
Second optimized Anti-structure
anti 4[5]
C1 -231.69097 1.06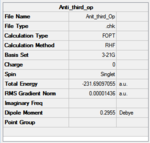
Third optimized Anti-structure
anti 2[6]
Ci -231.69254 0.08
Fouth optimized Anti-structure
gauche 4[7]
C2 -231.69153 0.71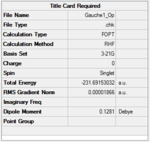
First optimized G-structure
gauche 3[8]
C1 -231.69266 0.00
Second optimized G-structure
gauche 1[9]
C2 -231.69167 0.62
Third optimized G-structure

As shown in the table above, the gauche 3 conformer is the lowest energy conformer by HF calculation. This is quit surprising as antiperiplanar arrangement (anti conformer) would usually be the more stable conformation due to the reduced steric hindrance and possible orbitals aliment. However,this unexpectedly low energy can be explained by examining the molecular orbitals of the conformer:

Molecular Orbitals
Anti 1 Gauche 3
HOMO


As can be seen in above MO diagram, there is some electron density between the 2 pi-orbitals of the two alkenes in Gauche 3 but not in Anti 1, indicating an interactions between the two orbitals. This secondary orbital overlap provide favorable interactions that lowers the energy of the conformer, making it much more stable than expected.

However, anti 1 and anti 2 both are very close in energy to the gauche 3 conformer (only 0.04 and 0.08 kcal/mol higher in energy respectively). Because of the fact that HF method is somewhat a lower level theory and does not take into account of empirical data, it is possible that the real lowest energy conformer might not the the gauche 3 conformer. In order to determine the true lowest energy conformer, a higher level theory must be used to better approximate the real structures.

DFT/B3LYP

The DFT/B3LYP method, while based on a theory much like the HF, it also takes into account of emprical data, making it an semi-empirical method for calculation. The HF optimized structures of interested (Anti 1, Anti 2, Gauche 3) were further optimized using DFT/B3LYP as method and 6-31G d as basis set. The results are shown below: (note: Because of the use of different theory, direct comparison of the energies between HF and DFT are meaningless and the relative energies are used instead. )

B3LYP Optimized structures
Conformer Structures Point groups Energy in Hartrees Energy in kcal/mol Sum of electronic and zero-point Energies at 0K Sum of electronic and thermal Energies at 298K Optimization summary
Anti 1[10]
C2 -234.61179 0.00 - -
'Re optimized of Anti1 busing B3LYP
Anti 2[11]
Ci -234.61170 0.06 234.469212 234.461856
Re optimized of Anti2 busing B3LYP
Gauche3[12]
Ci -234.61133 0.29 - -
Re optimized of Gauche3 busing B3LYP

As shown in the data above, Gauche 3 is no longer the lowest energy conformer under the DFT/B3LYP theory but remains very close to the other two conformers. Anti 1 has the lowest energy under this theory with Anti 2 being only 0.06kcal/mole higher in energy. This suggests that, although the secondary orbitals overlap in Gauche 3 greatly lowered its energy, the steric preference of the antiperiplanar conformation in Anti 1 and Anti 2 has a larger effect on the overall stability of the structure.

This kind of situation is quit often encounter in organic chemistry, where two types of interactions compete with one and other (Steric VS Orbitals overlap). The extend of the interactions are often very difficult to predict if one rely solely on chemical intuitions. In these situations, computational analysis are extremely useful as it allows a much more accurate prediction without conducting "bench chemistry".

Optimizations of Transition states

There are two possible transition states (TS) for the cope reactions: Chair TS and Boat TS. For a given 6 member ring, for example cyclohexan, chair conformation generally is the lowerest energy structure, as there is no angle strain (all 109.5), all C-C bonds are anti-peraplanar to each other and all the substituents bonded to the ring carbons are pointing as far away from each other as they can (reduces steric)[13]. Hence the chair TS seems to be the obvious choice as it would likely to be the lower energy TS and therefore the more likely TS in the reaction pathway.

However, there are many other factors that can effect the stability of a TS as well as which pathway the reaction take place. Therefore in the following part, the structures of both TS are drawn and optimized but with different methods. From the results of these calculations, the activation energies for both TS would be found and hence deteremining which TS the cope rearrangment proceed by.

Chair

Force Constant Matrix (FCM)
[14]

Provded a "good guess" can be made about the TS, the FCM is one of the easiest and fastest method for optimizing a TS. In the case of cope rearrangement, a H2C-CH-CH2 fragment was first made and optimized at HF/3-21G level theory to generate the lowest energy structures. Then two of the same fragment were combined in one molecule group so that the central carbon of one of the fragment is pointing at the opposite direction to the other fragment. The distance between the "terminal carbons" of the two fragments were adjusted to be roughly 2.2 A apart, the molecule group was then optimized (Opt+Fre) to a transition state (TS Berry) with keywords "opt=NoEigen" to ensure only one imaginary vibration would be obtained.

Freezing Bond Coordinate

Especially the same as FCM method, except bond distances of certain part of the molecule were first frozen while the rest of the molecule are allowed to relax and optimized. This is done by using the redundant coordinates option in gaussview, fixing the "bonds distance" to 2.2A and run an optimization of the molecule. The "correct bond distances" were then derived by unfreezing the bonds and change the setting to "derivative" in a new optimization.

Boat

QST2 Calculation

In cases where the structure of the TS is somewhat unclear, the QST2 would potentially be a better method than FCM. In this method, the structure of the reactant and the products were input into gaussview. The calculation would then try to find the middle point where the TS lie, this however, stills required some structure rearrangement to make the reactants and the product to be somewhat slightly closer to the TS as well as the numbering of the molecules must be exact. Failure in either of them would result in incomplete or wrong calculations.

Results summary

To compare the results of different theory, both HF optimized TS were futher optimized with DFT/B3LYP. All the results are summerised in the table below:

Transition states
Chair Boat
Method used HF(Freezing bonds method)[15] B3LYP[16] HF (QST2)[17] B3LYP[18]
Structure
Optimisation Summary
Converged ?
Imaginary Vibrations (cm-1) -817.93 -565.54 -839.96 -530.36
Visualization of vibrations Imaginary Vibration Imaginary Vibration Imaginary Vibration Imaginary Vibration

As shown in the table above,

The imaginary vibration correspond to the reaction coordinate and hence can be used as an indicator to see if the correct TS was obtained. All four vibrations (HF Chair, B3LYP Chair, HF Boat, B3LYP Boat) showed the same vibrations motions (but different in frequencies) where two of the "terminal carbons" comes together while the opposite "terminal carbons" move away from each other. This correspond to the cope rearrangement, where a C-C bond is form on one end as the opposite C-C bond was broken on the other end. Only one imaginary frequency was obtained for each TS.

Reaction pathway

IRC

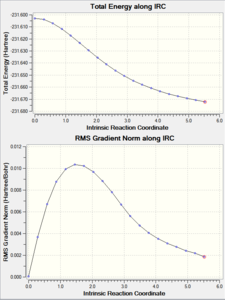
IRC is calculated by for both chair and Boat TS, and the difference between the number of Force constant calculated are also demonstrated in the table below:

IRC table
Chair IRC Boat IRC
Force constant calculated : Once [19] Force constant calculated : always [20] Force constant calculated : Once [21] Force constant calculated : always[22]
Product Structure
IRC Graph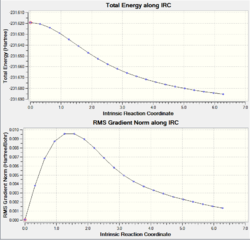

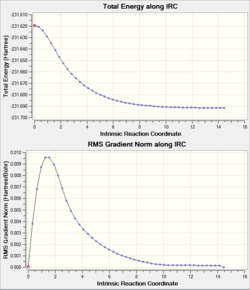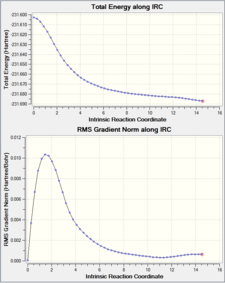Calculating the force constant once gave a much shorter and faster calculation (only around 21 steps) whereas calculating the FC always gave a much longer (50+ steps) calculation. The differences between "always" and "once" is not massive, as shown in the jmol files, the bond lengths hardly change at all but the "always" calculations gave a wider angle than the "once" calculation.

Products optimization
Optimized products
Chair Boat
Structure
Optimisation Summary
Converged ?

The two optimised products are obviously the same molecule but have slightly different conformation as can be seen in both the structures (joml) and in the energy summary. This occurs as a result of the two reaction paths arriving at different geometries based on the shape of the TS. The interesting thing is that the Boat product gives a more stable (lower in energy) product than the Chair one. This suggests that while the kinetically the chair reaction path may be more favorable, the Boat reaction path is the slightly more thermodynamically favorable one. The difference however, is quit small and therefore unlikely to have a big influence on the overall reaction.

Activation Energies (Ea)

The energies of the molecule were obtained by opening their frequency .log file in WordPad. Ea of chair for example are calculated as followed:

Ea (Chair) in kcal/mol =( E of Chair in a.u. - E of Anti 2 in a.u. ) x 627.509

Same calculations were carried out with Boat conformer. The results of the energies are shown in below table:

Energies (in kcal/mol) summary table
HF B3LYP
- Energy in kcal/mol Sum of electronic and zero-point Energies at 0K Sum of electronic and thermal Energies at 298.15K Energy in kcal/mol Sum of electronic and zero-point Energies at 0K Sum of electronic and thermal Energies at 298.15K
Anti 2 -231.69254 -231.539540 -231.532566 -234.61170 -234.469212 -234.461856
Chair -231.61932 -231.466700 -231.461341 -234.55698 -234.414929 -234.409008
Boat -231.60280 -231.450929 -231.445301 -234.54309 -234.402342 -234.396008
Activation Energies (Ea in kcal/mol) summary
Experimental values HF B3LYP
- Energy in 0K Sum of electronic and zero-point Energies at 0K Sum of electronic and thermal Energies at 298.15K Sum of electronic and zero-point Energies at 0K Sum of electronic and thermal Energies at 298.15K
Ea of Chair 33.5 ± 0.5 45.7 44.69 34.1 33.2
Ea of Boat 44.7 ± 2.0 55.6 54.8 42.0 41.3

As shown in the tables above, the chair conformer has a much lower energy than the boat conformer (around 10 kcal/mol less)in both HF and B3LYP theory as well as experimental values. This is as expected, chair conformer has less steric hindrance as explained in the start of the project, therefore the energy gap between the reactant and TS is smaller for Chair TS than for Boat TS. However, the activation energy does not necessarily always determine the reaction pathway, for many cases, the reaction goes via a TS that is higher in energy produce product that are much lower in energy, making it the thermodynamically more favorable reaction pathway.

The calculations also shows that the results obtained by DFT/B3LYP method are much closer to the experimental results than the HF theory. This shows that the semi-empirical DFT/B3LYP,6-31Gd theory is better suited method for solving the Schrodinger equation in this case. This is no big surprise as the DFT/B3LYP method is a higher level theory and 6-31Gd (d = polarization function for heavy atoms)has much more functions than 3-21G as basis set.

Diels-Alder

Demonstration of Diels-Alder (DA): Butadiene and Ethylene

Ever since the discovery of the reaction between diene and dienophile by Otto Paul Hermann Diels and Kurt Alder in 1928[23]. The diels-alder reaction has been one of the most well known reaction in organic chemistry, as it provide a relatively simple synthetic route for ring structure, as well as being a classic example of cyclo-addition which is commonly used as text-book example. Hence, not surprisingly a large number of studies had been done on it both computationally and experimentally. To demonstrate this reaction in simple terms, diene and dienophile with the least amount of substituents were used in this project: Butadiene and Ethylene. While they might not be the best choice for diels-alder reagents (DA reaction works best with electron deficient dienophile as it can better accept electrons from the diene), the simplicity of this example allows us to use more basic theory, keeping the calculation time short but still produce reasonable results.


Reaction Scheme for DA between Butadiene and Ethylene

Reactants

Both reactants were drawn in gaussview and their structures were optimized using semi-empirical/AM1 method. As mention before, while this method is less sophisticated, it takes significantly less time compare to other method and hence was chosen as the initial method for calculation.

Optimized Structures
Butadiene[24] Ethylene[25]
Structure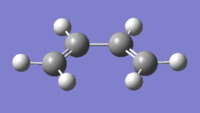
Optimization Summary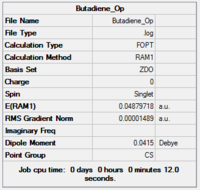
Converge?
HOMO
LUMO

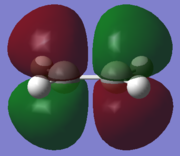An "Allowed" DA reaction involve a significant overlap between the HOMO of one reactant and the LUMO of the other. In order for 2 orbitals to interact, they must have the same symmetry. As shown in the MOs above,the HOMO of the ethylene and the LUMO of the butadiene both have symmetry s and the LUMO of ethylene and the HOMO of butadiene both have symmetry a.

Symmetry table
Symmetric Anti-Symmetric
symmetric alone the plane
antisymmetric alone the plane

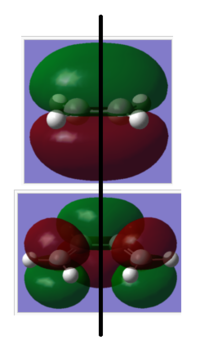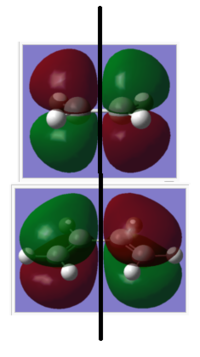Transition States

There are many methods can be used to determine the transition states of the Diels-Alder reaction. Since we have a very good ideal about the reaction pathway based on our understanding of the chemistry, a pretty "good guess" can be made about the approximate shape of the transition state. Hence the bonds freezing Force Constant Calculation method was used.

Optimization

The distances between the two terminal carbons where the two bonds were expected to form during the reaction was first froze while the rest of the molecule optimised, the resulting molecule were then further further optimised with the "bonds" set to "derivative". The resulting TS is shown below:

Summary table
TS obtained by semi-empirical/AM1
Structure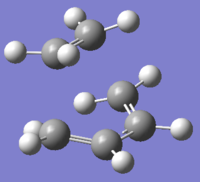
[26]
Optimisation Summary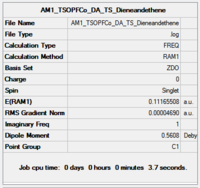
Converged ?
Visualization of vibrations Imaginary Vibration at -955.78(cm-1)

The structure of the TS is what we expected to see. There is only one imaginary vibration and it correspond to the reaction coordinate where the terminal carbons comes closer together at the same time in the same way that we expect the bonds to form. The bond length of the about-to-be-formed C-C bond is around 2.12A as shown in the jmol file.

MOs and Vibration
Summary table
TS obtained by semi-empirical/AM1
Energy Levels
HOMO
Anti-Symmetric
LUMO
Symmetric
Visualization of vibrations Imaginary Vibration at -955.78(cm-1)

Using the same rule as we did for the reactants, we can see that the LUMO has symmetry S (Symmetric alone an imaginary plane going through the middle) and the HOMO have symmetry A (Anti-Symmetric alone an imaginary plane going through the middle). Looking at the MOs of the TS, we can see that the HOMO is formed by the overlap between the HOMO of the butadiene and the LUMO of the ethylene, whereas the LUMO is formed by overlapping the LUMO of the butadiene and the HOMO of the ethylene. Therefore this reaction is "allowed" as the HOMO of butadiene (one reactant) can interact with the LUMO of ethylene (the other reactant) and vice versa.

There is only one imaginary vibration which again correspond to the reaction path where the two terminal carbons on the diene and the two on the ethylene moves closer together just like what they would do if they were to form a bond.

Products

Optimized product
Product Structure IRC Graph IRC Animation
[27]
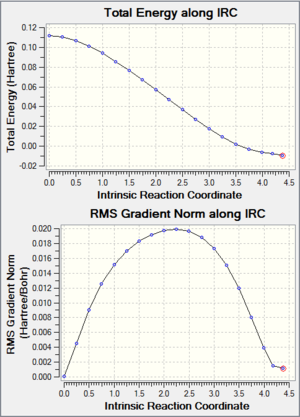IRC Animation

Selectivity of Diels-Alder : Cyclohexa-1,3-diene and Maleic Anhydride

One of the reason why DA is such a famous reaction is its somewhat unusual selectivity. With suitable substituents, 2 products might be formed from a DA reaction: endo and exo product. Which product formed depends on which TS is reach, experimentally, the endo product usually is the major product[28]. However, the endo product is not the thermodynamically more stable product, when under thermodynamic control, the exo product dominate. That suggests the endo product is the kinetic product and it's TS would be more stable (lower in energy) and hence have a lower activation energy.

This is thought to be because of secondary orbitals overlap occurs in the endo TS and hence stabilized the structure. However, this might not be the case for all diels-Alder as not all reactant's orbitals have the correct symmetry to interact. In this project, the selectivity of the reaction between Cyclohexa-1,3-diene and Maleic Anhydride was studied.

Structure Optimization

First the structure of both reactants needs to be optimized, two method were used : Semi-Empirical/AM1 and DFT/B3LYP.[29][30]

The TS of all 4 molecules were calculated using bond freezing FCM methods with Semi-Empirical/AM1 and DFT/B3LYP.

Transition states
EXO ENDO
Method used AM1[31] B3LYP[32] AM1[33] B3LYP[34]
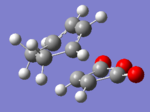
Structure
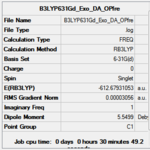
Optimisation Summary
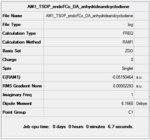
Converged ?
Imaginary Vibrations (cm-1) -813.06 -448.37 -806.26 -446.62
Visualization of vibrations Imaginary Vibration Imaginary Vibration Imaginary Vibration Imaginary Vibration

The AM1 calculation showed that the Endo structure is 1.68 kcal/mol lower in energy than the EXO TS, suggesting the ENDO TS is the more stable TS. The B3LYP calculation agree with this with the ENDO TS being 2.56 kcal/mol lower in energy than the EXO TS. This is further conformed by looking at the distance between the terminal carbons where the two sigma bonds were expected to form (shorter in ENDO TS than the EXO TS). This can be explained by comparing the structure of the two TS.

The exo TS is more strained as the carbons opposite to the CO-O-CO fragment is sp3 in exo but is sp2 in endo. The sp3 carbons have one of their hydrogen pointing closer to the CO-O-CO fragment whereas the sp2 carbon have all of it's hydrogens pointing away from the CO-O-CO fragment , this results in the exo TS being the more sterically unfavorable structure and hence higher in energy.

Molecular Orbitals

The MOs were generated to investigate the interactions between atoms:

MOs of Transition states
MOs HOMO-2 HOMO-1 HOMO LUMO LUMO+1 LUMO+2
AM1 EXO
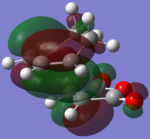B3LYP EXO
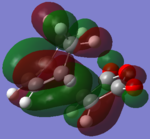AM1 ENDO
B3LYP ENDO

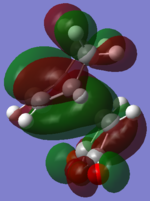The B3LYP method produced very similar MOs to the AM1 MOs, with a few noticeable exceptions (for example, HOMO-2 of the ENDO and the LUMO+2 on the EXO). The HOMOs are very much the same for both exo and endo, showing a large electron density where the bonds were expected to form. The orbitals on the (C=O)-O-(C=O) fragment are much smaller than the rest of the molecule and is not interacting with any other orbitals. The LUMO+2 for ENDO showed a electron density between the C=O)-O-(C=O) fragment and the two "opposite carbons", this is an example of a secondary orbitals overlap. However, this MO is unoccupied and therefore does not have a lots of effect on the stabilization on the TS. Overall, the B3LYP recognized a few more interactions than the AM1 method but no significant different between the two method in terms of the MOs.

Reaction pathway

IRC
IRC table
EXO ENDO
AM1[35] B3LYP[36] AM1[37] B3LYP[38]
Product Structure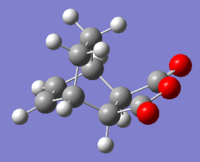
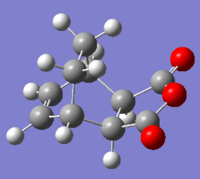IRC Graph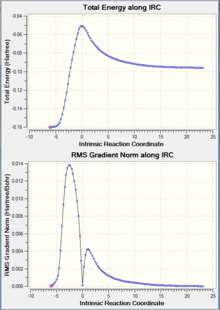
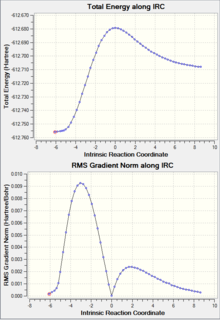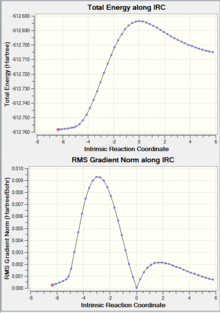IRC Animation Animation Animation Animation Animation

As shown in the table above, IRC calculation for all four TS resulted in the correct (with slight different between one another) corresponding products. However, the forward IRC for the two EXO TS and the B3LYP ENDO TS gave reactants, whereas the corresponding backward calculation generate the products. This might be due to the position of the TS (closer to the reactant vs closer to the product) or simply a calculation error.


References :

  1. ↑ ^ Arthur C. Cope; et al.; J. Am. Chem. Soc. 1940, 62, 441
  2. ↑ A Synthesis of Ketones by the Thermal Isomerization of 3-Hydroxy-1,5-hexadienes. The Oxy-Cope Rearrangement Jerome A. Berson, Maitland Jones, , Jr. J. Am. Chem. Soc. 1964; 86(22); 5019-5020.
  3. ↑ http://hdl.handle.net/10042/to-12276
  4. ↑ http://hdl.handle.net/10042/to-12277
  5. ↑ http://hdl.handle.net/10042/to-12278
  6. ↑ http://hdl.handle.net/10042/to-12279
  7. ↑ http://hdl.handle.net/10042/to-12280
  8. ↑ http://hdl.handle.net/10042/to-12281
  9. ↑ http://hdl.handle.net/10042/to-12282
  10. ↑ http://hdl.handle.net/10042/to-12283
  11. ↑ http://hdl.handle.net/10042/to-12284
  12. ↑ http://hdl.handle.net/10042/to-12538
  13. ↑ J. Clayden, N. Greeves, S. Warren, and P. Wothers, Organic Chemistry, p456
  14. ↑ http://hdl.handle.net/10042/to-12658
  15. ↑ http://hdl.handle.net/10042/to-12660
  16. ↑ http://hdl.handle.net/10042/to-12661
  17. ↑ http://hdl.handle.net/10042/to-12659
  18. ↑ http://hdl.handle.net/10042/to-12662
  19. ↑ http://hdl.handle.net/10042/to-12666
  20. ↑ http://hdl.handle.net/10042/to-12664
  21. ↑ http://hdl.handle.net/10042/to-12665
  22. ↑ http://hdl.handle.net/10042/to-12663
  23. ↑ Diels, O., Alder, K., Justus Liebig's Annalen der Chemie 1928, 460, p98–122
  24. ↑ http://hdl.handle.net/10042/to-12668
  25. ↑ http://hdl.handle.net/10042/to-12667
  26. ↑ http://hdl.handle.net/10042/to-12669
  27. ↑ http://hdl.handle.net/10042/to-12670
  28. ↑ W. C. Herndon, C. R. Grayson, J. M. Manion, J. Org. Chem., 1967, 32 (3), 526–529
  29. ↑ http://hdl.handle.net/10042/to-12671
  30. ↑ http://hdl.handle.net/10042/to-12672
  31. ↑ http://hdl.handle.net/10042/to-12673
  32. ↑ http://hdl.handle.net/10042/to-12676
  33. ↑ http://hdl.handle.net/10042/to-12674
  34. ↑ http://hdl.handle.net/10042/to-12675
  35. ↑ http://hdl.handle.net/10042/to-12679
  36. ↑ http://hdl.handle.net/10042/to-12677
  37. ↑ http://hdl.handle.net/10042/to-12680
  38. ↑ http://hdl.handle.net/10042/to-12678
Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod:chilong_module3&oldid=818880"