Rep:Mod:chilong module1

Molecular mechanics and semi-empirical molecular orbital methods for structural and spectroscopic evaluations

Molecular Mechanics

The Hydrogenation of Cyclopentadiene Dimer

Diels-Alder Reaction

Reaction between 2CPD

The reaction between 2 cyclopentadiene (CPD) can produce 2 products: endo and exo dimer. Experimentally, the endo product usually predominate. However the endo is not the thermodynamically more stable product, when under thermodynamic control, the exo product dominate. This suggest the exo product would be more energetically favorable structure of the two. To confirm this computationally, ChemBio3D is first used to generate the structure of the 2 products, then MM2 calculation is used to minimized the energy of the structure in order to obtain the lowest energy structure for both products. The structures (from MM2 minimization) and results of the calculation are shown below:

MM2 calculations	EXO	ENDO
Stretch	1.2849	1.2498
Bend	20.5815	20.8492
Stretch-Bend	-0.8379	-0.8355
Torsion	7.6554	9.5109
Non,1,4 VDW	-1.4174	-1.5434
1,4 VDW	4.2324	4.3190
Dipole/Dipole	0.3775	0.4475
Total (kcal/mol)	31.8765	33.9975

As shown in the calculation, the exo product is indeed the thermodynamically more stable product (the exo structure's energy is 2.121 kcal/mol lower than the endo one) and the torsion is the major contributor to this instability in endo product. However, as mention before, the endo product is often found to be the dominating product. This suggest the endo dimer is the kinetically more favorable product, meaning the transition state it formed during the reaction have a lower energy barrier than the exo dimer, hence formation of endo dimer is faster and also irreversible under non-thermodynamic control (under thermodynamic control, formation of endo product becomes reversible and equilibrium would lies to the more energetically favorable site and hence exo product predominate). This can be explained by the secondary orbital overlap occurs between the diene and the dienophile during endo transition state of the reaction. This stabilization, however can not be account for using MM2 as it only takes into classical model and does not include quantum mechanical influence (No Molecular Orbitals involve in the calculation).

Hydrogenation

Hydrogenation of the Endo product

The same calculation are performed with the 2 hydrogenated dimers (X and Y)

MM2 calculations	X	Y
Stretch	1.2789	1.0970
Bend	19.8573	14.5254
Stretch-Bend	-0.8348	-0.5492
Torsion	10.8108	12.4979
Non,1,4 VDW	-1.2211	-1.0707
1,4 VDW	5.6318	4.5111
Dipole/Dipole	0.1621	0.1406
Total (kcal/mol)	35.6850	31.1520

As shown in the table above, the structure of Y is at a lower energy state than X (kcal/mol lower than X). Therefore under thermodynamic control, Y would be the major product and X would be the minor product. In this case, however, the bending energy is the major contributor to the difference in energies (X is kcal/mol higher than Y). Looking at the double bonds in both X and Y, both double bonds are forced to bend away from their prefered geometry (sp2, 120 degree) due to ring strain, this will rais the overall energy of the structure and hence the more the bending, the higher the energy of the structure. Although usually 6-member ring has less strain than 5-member one, the bridge head carbon in the 6-member ring makes it even less flexible then the 5-member one so the double bond in X is more distored than Y (can easily be seen when comparing the 3D models ), hence making the structure of X less stable (higher in energy).

Stereochemistry and Reactivity of an Intermediate in Synthesis of Taxols

Taxol 10, with CO down

Taxol, an antileukemic and antitumor drug commonly made from Taxus brevifolia . During its synthesis proposed by Paquette, two key intermediates 9 and 10 are produced with the difference being the CO group point up in 9 and down in 10. The two molecules are an examples of Atropisomers, these isomers arises due to the inability to freely rotate a single bond (a higher energy barrier exists between the 2 isomers), usually as a result of steric demand, and are most commonly found in rings with macrocyclic structures.

Taxol 9, with CO up

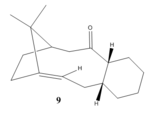
At room temperature, the isomers can inter-convert to one another but will end up with the more stable isomer. The stability of the two intermediates can be studied by first using ChemBio3D to draw out different conformations of each isomer. Then with the help of MM2 and MMFF94 calculations, the energies of all these structures can be minimized and hence allow the us to find out which intermediate (9 or 10) is the more stable isomer. list of possible conformations obtained are in the table below:

Energy calculations for Taxol intermediates

Calculations	Taxol 9 conformation 1	Taxol 9 conformation 2	Taxol 10 conformation 1	Taxol 10 conformation 2
Stretch	2.7832	2.8775	2.6211	2.7112
Bend	16.5400	17.2776	11.3426	11.7460
Stretch-Bend	0.4298	0.4739	0.3429	0.3235
Torsion	18.2561	20.6083	19.6754	21.8656
Non,1,4 VDW	-1.5545	-0.8987	-2.1690	-2.1004
1,4 VDW	13.1098	14.3799	12.8723	13.9193
Dipole/Dipole	-1.7249	-1.7084	-2.0023	-2.0317
Total MM2 (kcal/mol)	47.8396	53.0102	42.6830	46.4336
Total MMFF94 (kcal/mol)	70.5608	77.9732	60.5511	66.369
Conformation of the 6 member ring	chair	boat	chair	boat

As shown in the table, for either isomer (9 or 10) the chair conformations always have lower energy than the boat conformations (by 5.1706 kcal/mol for 9 MM2 and 3.7506 kcal/mol for 10 MM2). This is as expected, because chair conformations allows all the groups attached to the carbon ring to adopt stagger conformation, this reduces steric clashing and maximize sigma and sigma* orbitals overlap which again further lower the energy of the structure. However, both conformations of 10 (boat and chair ring) have lower energy than even the most stable conformation of 9 (chair), by as much as 5.1566 kcal/mol. Note that although the MMFF94 gives different energies (compare to MM2), they follow the same trend (chair < boat, 10 < 9 )

Hyperstable Alkene

The energies of the hydrogenated isomers are calculated the same way as the alkene isomers (MM2, MMFF94) in order to obtained the most stable structures:

Calculations	Taxol 9 conformation 1	Taxol 9 hydrogenated	Taxol 10 conformation 1	Taxol 10 hydrogenated
Stretch	2.7832	3.0243	2.6211	2.6735
Bend	16.5400	15.1943	11.3426	12.1091
Stretch-Bend	0.4298	0.5873	0.3429	0.5816
Torsion	18.2561	21.6090	19.6754	22.8383
Non,1,4 VDW	-1.5545	-1.4951	-2.1690	-2.6087
1,4 VDW	13.1098	15.6100	12.8723	15.5184
Dipole/Dipole	-1.7249	-1.7303	-2.0023	-1.7323
Total MM2 (kcal/mol)	47.8396	52.7997	42.6830	49.3798
Total MMFF94 (kcal/mol)	70.5608	77.9306	60.5511	69.5484
Conformation of the 6 member ring	chair	chair	chair	chair

As shown in the above table, the most stable form of the hydrogenated products are also in their chair conformations. The difference in energies, between the alkene forms and their saturated form are calculated, this is known as olefinic/allylic strain. Alkenes with negative allylic strain energies are classed as hyperstable alkene, and this in indeed the case, as the allylic strain of 9 and 10 are calculated as -4.9601kcal/mole and -6.6968 kcal/mole respectively.

This negative strain can be explained by comparing the geometry of the alkene and saturated forms. Alkene carbons are sp2 and have a preferred angle 120 degree, where as alkane carbons are sp3 and preferred angle at 109.5 degree. However, in the case of Taxols, the angles are distorted due to ring strain; the greater the deviation from the preferred angles, the more unstable the structure. Looking at 10, the bond angle for the alkene is 124 degree, which is only 4 degree deviation from the ideal angle, the alkane on the other hand has bond angle of 120 degree, which is a much greater deviation than the alkene forms, making alkane form much more unstable and hence the alkene is very uncreative toward hydrogenation.

Semi-empirical Molecular Orbital Theory

Regioselective Addition of Dichlorocarbene

Compound 12 can react with dichlorocarbene forming one or more of the products 13-15 via cycloaddition on one or both of the alkenes. Which would be the major product depends on the reactivity of the corresponding alkene functional group. More specifically, the more nucleophilic alkene would dominate the reaction.

Reaction between coumpound 12 and dichlorocarbene

Molecular Orbitals

In order to determine the reactivity, the molecular orbitals of compound 12 are required. To achieve this, the energy of the 12 was first minimized using MM2, then the MOs are generated by Mopac calculation. The results are shown as follow (note: the structure provided are after both MM2 and Mopac calculation):

MM2 calculations	Product 12
Stretch	0.6185
Bend	4.7327
Stretch-Bend	0.0399
Torsion	7.6615
Non,1,4 VDW	-1.0638
1,4 VDW	5.7932
Dipole/Dipole	0.1124
Total (kcal/mol)	17.8945

MOs

MO	ChemBio3D	Gaussian
HOMO-1	HOMO-1	HOMO-1
HOMO	HOMO	HOMO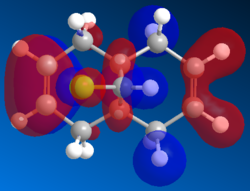
LUMO	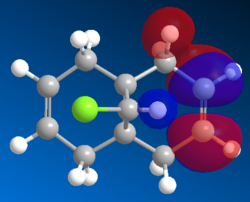LUMO	LUMO
LUMO+1	LUMO+1	LUMO+1
LUMO+2	LUMO+2	LUMO+2

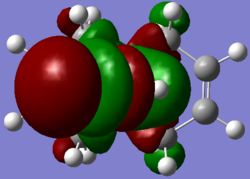As the molecule is symmetrical, the MOs are expected to be symmetrical as well. From the diagrams shown above, some of the MOs generated by ChemiBio3D using Mopac/PM6 calculation, All the MOs, especially the HOMO-1, LUMO and LUMO+1 shows a lack symmetry (due to a 'bug' in the program) whereas the Gaussview MOs shows perfect symmetry for all MOs. However, another notable difference is the LUMO+1 and LUMO+2 exchange from Mopac to Gaussian.

The electrophile (dichlrocarbene or mCPBA) would react with the electrons in the highest occupied molecular orbital (HOMO). The electron density of this MO would be most relevant in determining the reaction site. As shown in the HOMO generated by Mopac, large amount of electron density are localised on the endo alkene (the alkene on the Cl side). Hence endo alkene is the more reactive of the two.

Looking at the lower energy and less reactive HOMO-1, the electron density are shown to be more heavily localised on the exo alkene. This stabilisation can be explain by the interaction between the σ* C-Cl and the π orbital of the exo alkene. This donation from π orbital into the σ* C-Cl is supported by the LUMO+2 (in Gaussian).

IR analysis

MOPAC/RM1 was used to generated the IR spectra of compound 12 and 11

Product of hydrogenation of exo alkene of 12

InfraRed spectra

12	11
12	11

InfraRed spectra peaks list

Functional groups	C-Cl	C=C exo	C=C endo
Stretching frequency in 12 (cm-1)	770.84	1737.11	1757.58
Stretching frequency in 11 (cm-1)	774.97	-	1758.07

The C-Cl stretch in 12 is at 770.84cm^-1 and 774.97cm^-1 for 11. Both with high intensity due to the large change in dipole moment, however, the stretch in 11 has higher intensity than 12. This is likely due to the present of the double bond in 12 reduces the dipole moment of the C-Cl stretch (double bond has higher electron density than single bond, hence reducing the electron density difference between the "Cl side" and the "C side" ). The difference in frequency of the C-Cl is due to the donation of π orbital of the exo alkene into the σ* C-Cl in 12, weakening the C-Cl bond. This is in good agreement with the 2 C=C stretch in 12, 1757.58 (endo) and 1737.11 (exo), the overlap between the σ* C-Cl and the π orbital of the exo alkene lowering the electron density of the exo alkene (hence lower stretching frequency). There are almost no difference between the endo C=C of 12 and 11, however, like all the C=C mentioned above, have very low intensity due to the symmetrical nature of the C=C and hence the really small change in dipole moment.

Glycosidation

Reaction scheme (from instruction)

Glycosidation of, for example, glucose involve an nucleophilic attack from a nucleophile (e.g. alcohol) at the anomeric centre (the OH is usually substituted by a leaving group X) of glucose. This however, results in mixture of α and β anomer products as attack from both above and below the sugar ring are possible.

However, with the help of certain protecting groups next to the anomeric centre, selective formation of α or β anomer is possible. This is known as neighboring-group-participation. OAc group is a classic example of such reaction (shown on the right), the selectivity of glycosidation of OAc protected sugar depends on the position of the OAc group.

To form the α anomer, the OAc group must be above the ring, forcing the Nu to attack from below, for β anomer, OAc occupied the bottom face and hence only way Nu can attack is from above.

In order to explain and conform these facial preferences computationally, the 'backbone' of the structures must be drew first, which mean choosing a suitable R group. Me was chosen to be the protecting group (R), as it is simple and one of the least computationally demanding functional group (as opposed to Bn or OAc). This minimized the effect of R on the molecule and simplify both the calculations and the structure of the molecules.

Once the structures of all molecules were drew in ChemBio3D, MM2 and Mopac/PM6 were used to minimized the energies and the lowest energy structure of each molecules were obtained. The results are summarized in the table below (note the jmol files are the structures obtained from Mopac):

Energy calculations

Calculations	A	A'	B	B'	C	C'	D	D'
Stretch	2.8273	2.7128	2.8168	2.4015	2.0564	2.8975	1.8003	2.7389
Bend	11.8873	10.7931	10.7187	9.9735	13.7199	18.2511	18.7533	19.2384
Stretch-Bend	1.0759	0.9973	0.9887	0.8244	0.7351	0.8952	0.7741	0.7792
Torsion	3.1464	5.1803	2.5385	2.6832	9.6551	9.3164	9.5192	8.7200
Non,1,4 VDW	1.4576	-1.7	0.8510	-0.7391	-2.6563	-2.0574	-3.6479	-2.5646
1,4 VDW	18.9623	19.5760	18.9266	19.8316	17.8862	19.0901	17.7474	19.0171
Charge/Dipole	-25.5818	-2.4503	-21.4518	-21.4809	-9.9100	1.7988	-6.8739	-6.1248
Dipole/Dipole	5.9095	5.8528	5.5051	5.7920	-2.2267	-1.5542	-1.4205	-0.6578
Total MM2 (kcal/mol)	19.6845	40.962	20.8935	19.2862	29.2597	48.6376	36.6520	41.1464
Total Mopac/PM6 (kcal/mol)	-91.64876	-77.41885	-88.73028	-76.54256	-91.65862	-66.84832	-88.53712	-65.52222

The MM2 calculation is not as good for this exercise as Mopac, because it does not take into account of quantum mechanics, therefore molecular orbitals interaction such as anomeric effect would not be included in the calculation. From the above table, it is clear that all A,B,C,D are more stable than their corresponding A',B',C',D' in the Mopac calculation. Meaning thermodynamically, formation of C and D is more favorable and therefore likely to be the dominating intermediates, hence the selectivity. This could be because the carbonyl oxygen in A/B/C/D are closer to the oxonium oxygen, better stabilizing the charge. As can be seen that A and C have more Charge/Dippole interaction than A' and C'. The same trend is expected to be between B/B' and D/D' too, however, the MM2 calculation for them appeared to be inaccurate.

Another way to explain the selectivity is by inspecting the trajectories of attack. If an imaginary bond is drew between the carbonyl oxygen and the oxonium carbon in A/A' and B/B', the trajectory of attack can be approximated as follow:

Angle of attack of A	Angle of attack of A'	Angle of attack of B	Angle of attack of B'

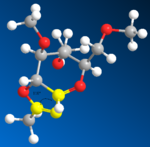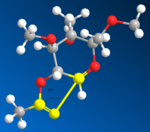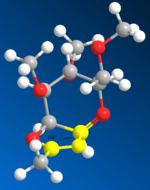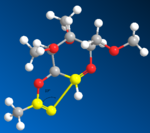As shown in the above diagrams, the angle of attack is around 110 degree for A and B, 89 degree for A' and B'. This clearly showed that A' and B' are more distorted from its ideal angles (lone pairs of Oxygen are normally 107 degree away from the C=O double bond). Because of this, the reaction from A --> C would be much faster than A' --> C' (B --> D better than B' --> D'). Therefore If A is the starting material, C would be the predominate intermediate, hence forcing the Nu to attack from the other side, and as a result selectively forming beta-anomer. On the other hand, if B is the starting material, D would be the major intermediate, hence resulting in alpha anomer.

Similar reasoning can be used to account for the differences in energies between C and C', D and D'. C' and D' have greater deviation from the ideal angle, therefore is more strained and more unstable.

A and A' are slightly more stable than B and B', so are C and C' slightly more stable than D and D'. This could be due to the slight 1,3 diaxial strain that exists in B/B' and D/D' but not A/A' and C/C' (all large substituents are in equatorial position for A/A' and C/C').

For Mopac/PM6 calculation, A=C and B=D, this is because Mopac can recognized the bonding interactions between the carbonyl oxygen and the oxonium carbon even in A and B even without drawing a bond between them, to Mopac, C and D are simply A and B with that interaction drew as a solid bonding, the extend of interaction does not change.

Mini project: 1,3-Cycloaddition

Reaction scheme

In a recent literature the reaction between Oxime and cyclopentadiene (CPD) were carried out and expected to generate product 2 via 1,3-cycloaddition. However,the lack of electron-withdrawing groups in CPD results in the formation of side product 3 and 4 via 1,4-cycloaddition(aza-Diels-Alder reaction). Various NMR spectroscopes were used in the literature to confirmed the structure of all the products. In this mini-project, computational analysis on these products were carried out and the results were compared to the experimental data obtained from the literature.

Structures Optimization

To obtain the correct conformation of all the products, their structure's energies were first minimised with MM2, followed by Mopac/PM6 in ChemBio3D. The resulting structures were then uploaded to be refined by Gaussian calculation (methods: DFT=mpw1pw91, Bassis: 6-31G(d,p)). Due to the nature of the molecules small size and lack of conformational freedom, calculations were all done in relatively short time.

Results of optimization

MM2

Molecules	Product 2	Product 3 EXO	Product 4 ENDO
Stretch	0.9161	1.5291	1.2656
Bend	12.1583	21.1207	21.7631
Stretch-Bend	0.1899	-0.3691	-0.4025
Torsion	4.177	2.3840	1.8658
Non,1,4 VDW	-1.9671	-3.8011	-3.0018
1,4 VDW	6.8685	9.5681	9.1063
Dipole/Dipole	2.5164	-1.1536	-0.0914
Total (kcal/mol)	24.86	29.28	30.5051

As expected, the exo is the more thermodynamically stable product (lower in energy then endo), however the most stable form is product 2 (lowest energy), making it the predominate product. The difference in energy between 3 and 4 is not much, only by about 1.2 kcal/mol. meaning while the Exo would be the main side product, the difference would not be much.

Mopac PM6

The results of the minimized structures for all products are given below:

Product 2 Product 3 Product 4

NMR Analysis

The optimized structures from the previous step were used to obtained the NMR prediction (by sending the edited file to SCAN). The resulting spectra were observed under refernce TMS, DFT=mpw1pw91,6-31G(d,p),CDCl₃

Comparison of chemical shifts to literature values

Overall, the calculated C¹³ NMRs were in very good agreement with the experimental data provided by literature. The raw data obtained from calculation and experimental data are summarized in table below (publish data as references):

Table of all C¹³ NMRs of all adducts

	2 experimental	2 calculated	3 experimental	3 calculated	4 experimental	4 calculated
Chemical shift (ppm)	169.8	167.0	172.9	165.1	172.1	166.9
	137.7	136.8	138.1	143.1	139.5	139.8
	127.9	125.9	133.1	132.8	134.3	133.6
	91.9	92.3	70.4	71.5	72.9	73.6
	67.2	64.0	69.5	70.6	71.2	71.9
	52.0	53.0	52.2	51.2	51.9	51.1
	45.9	47.9	47.6	47,4	46.3	47.1
	34.5	36.2	45.3	46.9	45.3	46.6

C¹³ NMR spectra of all adducts

	Product 2	Product 3 exo	Product 4 endo
predicted C13 NMR)	2	3	4

On first sight, all the calculations for the carbonyl carbons (peaks around 170ppm) were all differ by a lot more than the others, however, this is due to systematic error for the calculation and therefore needs to be corrected by putting them in (0.96*chemical shift) + 12.2. The resulting chemical shifts for 2, 3, 4 are 172.5, 170.7, 172.4 ppm respectively. Now most the chemical shifts difference between experimental and calculation are less 3 ppm with exception of the second highest peak for 3.

Chart showing the difference between CORRECTED calculation results and experimental data

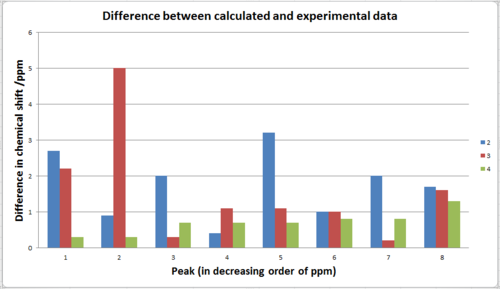
As shown from the graph above, the calculation generated an accurate prediction that is in good agreement with experimental data, the difference in ppm is less than 5 ppm and many of the peaks have error less than 1 ppm. While this degree of error is still consider big in H-NMR, in carbon NMR, the chemical shifts difference between different carbon environment are itself very big, making a few ppm difference an acceptable error.

2 can easily be distinguished from 3 and 4 using C¹³ NMR. The peaks at 92 and 35 ppm only present in 2 and correspond to the 2 carbons that are directly adjacent to the alkene functional group. On the other hand the spectra for 3 and 4 are almost identical in both experimental and computational results, with only around 1~2 ppm difference between one another.

Carbons assignment

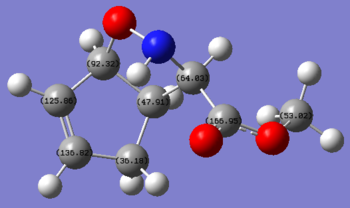
However, there is a great deal of difference in the assignment of the carbons for 3 and 4(2 are with very good agreement with literature values in both chemical shifts and assignment). This is not uncommon as assigning C¹³ NMR are often very difficult and without the help of computational analysis, many people would have to guess what some of the less obvious peaks correspond to which carbons. This is the case for all 3 products, the assignments given by the literature and calculations are shown below:

Table of all C¹³ NMRs of all adducts

Molecule	literature	calculated
2	Literature2	Calculated2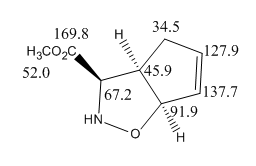
3	Literature3	Calculated3
4	Literature4	Calculated4

As shown in the literature assignments,apart from the carbonyl carbons, all other peaks are assigned differently for 3 and 4, for example, the 2 carbons that are directly adjacent to the alkene (carbon next to N and carbon near CO₂Me) have chemical shifts of 52.2 and 69.5 ppm respectively in 3 but are at 72.9 and 45.3 ppm respectively for 4.

The calculated assignments of 3 and 4 however are in good agreement with one another, with the exception of the carbon adjacent to the CO2Me group which change from 70.6 to 73.6 ppm from 3 to 4. This difference in chemical shifts can potentially be useful in distinguishing the exo and endo products, corresponding to the change in the CO₂Me from pointing up to down. A similar 'jump' in chemical shift from 69.5 to 72.9 ppm in the literature values is also observed, but the assignments given by literature failed to explain this, however, as the difference is only 3 ppm, even if the calculation is correct, this differences can easily be overcome by errors, hence not a very reliable tool.

IR Analysis

The same optimized structures from earlier step were used to obtained the IR prediction (by sending the edited (for IR) file to SCAN). Some of the more useful peaks are listed in table below:

IR spectra of all adducts

	Product 2	Product 3 exo	Product 4 endo
predicted IR	2	3	4

Notible IR peaks list

Functional groups	C-O single stretch	C=O stretch	N-H stretch	N-OH stretch
Stretching frequency in 2 (cm-1)	-	1828.19	3410.42	-
Stretching frequency in 3-exo (cm-1)	1301.75	1821.48	-	3805.58
Stretching frequency in 4-endo (cm-1)	1251.12	1837.85	-	3803.40

Although there are no literature spectra to compare the results, the predicted IR can still provide some information about the molecules that can potentially be useful in determining the structure and the maybe even the reactivity of the molecule (combined with other analytical techniques). The predicted spectra showed all the characteristic peaks one would expect based on the structures of the products. For example, the absent of N-OH stretch in 2, and the absent of N-H stretch for 3 and 4. One interesting differences between 3 and 4 is that the C-O (the O that is between two carbons) bond is stronger (higher wavenumber) in 3, where as the C=O ( the O that is bonded to only one carbon) bond is stronger in 4.

This changes in frequency from 3 to 4 are large (around 50 cm^-1 for C-O and 26 cm^-1 for C=O) and can therefore be useful in distinguishing between the two isomers, assuming the prediction is accurate. The changes in frequency are likely the results of the differences in conformation around the ester groups, for example if a C-H/C-C/even a lone pair is antiperiplanar to the σ C-O, donation from the lone pair or the σ C-H/C-C bond to the σ* C-O orbital can result in a reduction of bond order hence weaken the C-O, lowering the frequency. Similarly, donation into the π* orbital of the C=O, resulting pushing the double bond to the O, resulting in C-O^- which leads to decrease in bond order and again, lowering the frequency.

Conclusion

The results of this project showed that computational analysis can indeed be used in predicting and identifying different isomers. For non-complex molecules, relatively simple and quick calculations can generate results that are in good agreements with experimental data. while distinguishing between very similar isomers (in this case the endo/exo product, or optical isomers) can be difficult, regio-isomers can easily be identified using C¹³ NMR and maybe even IR as shown in the project. Other predictions, such as optical rotation and CD can also be carried out to help identifying the isomers, however, the molecules of interested are not optical isomers and the analysis performed were able to distinguish the isomers effectively. While the prediction of H-NMR were also obtained, the H-NMR require a very high accuracy to be useful (a difference fo 2 or 3 ppm indicate a completely different chemical environments, therefore prediction with error of +/- a few ppm would be essentially useless)

References: