Module 3: The Transition State

The Cope Rearrangement

Optimising Reactants and Products

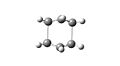
Anti-1,5-hexadiene

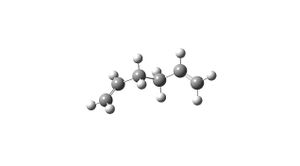
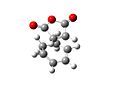
1,5-hexadiene was drawn in Gaussview, with the bonds anti across the central 4 carbons, and tidyed using the clean function. The molecule was then optimised using the HF/3-21G method. The resulting structure looked as follows(see image) and had an overall energy of -231.6926 a.u. The point group was C2.

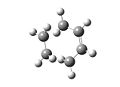
Gauche-1,5-hexadiene

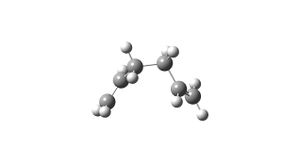
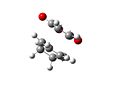
1,5-hexadiene was drawn in Gaussview, with the bonds gauche across the central 4 carbons, and tidyed using the clean function. The molecule was then optimised using the HF/3-21G method. The resulting structure looked as follows(see image) and had an overall energy of -231.6917 a.u. The point group was C2.

These results show that the anti conformation is more stable than the gauche as it has a lower energy (a difference of 2.363kJ/mol).

From the previous calculations, I would predict that the lowest energy conformation would be an anti conformation with the alkene groups pointing the opposite directions, as this would reduce steric hindrance.

Predicted Lowest Energy Conformation

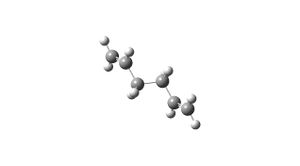
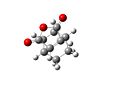
The molcule was drawn by inserting the atoms and bonds as usual but with modifying the dihedral angle across the central 4 carbons to 180 and the diheral angles across carbons 1,2,3 and 4 and 3,4,5 and 6 to 120 (going in opposite directions). The results from the optimisation gave an overall energy of -231.69254. The sum of the zero point energies is -231.539539 a.u.. The sum of the thermal enrgies at 298.15 K is -231.532565 a.u. The point group is Ci.

From looking at the structures, the first structure is anti1, the second structure is gauche2 and the third structure is anti2. The energies match those given in the table.

Anti 2 Conformation

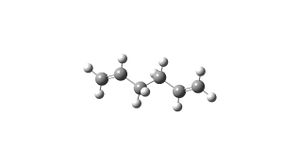
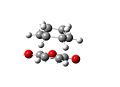
The anti 2 conformation has already been seen as the predicted lowest energy conformation, so the first optimisation has already been performed. The higher level optimisation is B3LYP/6-31G*. The results from this gave the overall energy to be -234.6117 a.u., which is alot lower than that given for the previous optimisation. The point group is still Ci. The dihedral angles between the last 4 carbons of the chain are 118.50°.

The frequency analysis gave the following vibrations:

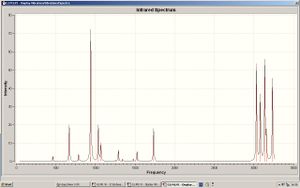
Vibrational Spectrum for 1,5-hexadiene(anti2)

No	Frequency	Intensity
1	669.79	20.16
2	940.35	70.91
3	1036.02	19.92
4	1068.04	9.7
5	1734.71	18.16
6	3031.43	53.55
7	3080.05	35.89
8	3136.98	56.05
9	3155.74	14.77
10	3234.05	45.47

The Frequency analysis gave the following results:

The sum of the electronic and zero-point energies = -234.469182 a.u.

This is the potential energy at 0K.

The sum of the electronic and thermal energies = -234.461844 a.u.

This is the energy at 298.15K and 1 bar pressure, it includes vibrational, rotational and translational components.

The sum of the electronic and thermal enthalpies = -234.460900 a.u.

This includes a correction for RT.

The sum of the electronic and thermal free energies = -234.500730 a.u.

This includes the entropic contribution to the free energy.

Optimising the 'Chair' and 'Boat' Transition States

An allyl group was drawn and optimised, giving the energy to be -115.8230 a.u (72679.27997kcal/mol). and the point group to be C2v.

A guess of the chair transition state was created by copying 2 of the optimised allyl groups into one molgroup and arranging them into the chair conformation. This then went under optimisation to a transition state and frequency analysis using the HF/3-21G method. The results showed that the energy was -231.6193 a.u. and the bond length between the terminal carbons is 2.0196 angstroms. There is an imaginary vibration at -817.989 cm-1.

The same guess for the chair transition state was optimised using a different method involving the redundant coord editor, used to freeze and derive the partial bond lengths. The resulting optimisation showed that the energy was -231.6193 a.u. and the bond length between the terminal carbons was 2.0207 angstroms. There is an imaginary vibration at -817.759cm-1. The zero-point energies were -231.466701 a.u., which gives the activation energy at 0K as 45.706 kcal/mol. The energies at 298.15K were -231.461341 a.u., which gives the activation energy as 44.693 kcal/mol at 298.15K. These activation enrgies are quite a bit higher than the experimental values.

The boat transition state was optimised using the optimised structure of the anti conformation of 1,5-hexadiene. Two copies of the molecule were placed in the same molgroup, one as the reactant and one as the product, the product was renumbered to correspond to the reactant and both molcules wre rearranged to have the dihedal angle over the central 4 carbons as 0 and the bond angles betwee the end crbons to be 100. A QST2 calculation was run to optimise the transition state resulting in an energy of -231.6028 a.u. and a bond length of 2.1398 angstrom between the terminal carbons. There is a small imaginary vibration at -840.008cm-1. The zero-point energies were -231.450926 a.u., which gives the activation energy at 0K as 55.605kcal/mol. The energies at 298.15K were -231.445297 a.u., which gives the activation energy as 54.761kcal/mol at 298.15K.

The imaginary vibrations for both the chair and the boat transition states show that one end of the allyl goups move towards each other as the other ends move apart. This shows that as one bond is broken, another is formed in a concerted mechanism, which is correct for the cope rearrangement as it is pericyclic.

An IRC method, using 50 points, was run on the chair transition state to find out which conformer would be produced as the final product. After the first run the results gave the energy as -231.680488 a.u. This wasn't the final minimised geometry, to find the minmised geometry 3 methods were tried.

The resulting molecule was optimised using the RHF/3-21G method and the results gave the energy as -231.691667 and had a point group of C2/C1. The image looks like the gauche2 conformer. This could be the final minimised geometry but it could also be a false minimum if the IRC was too far away from the actual minimum as the optimisation will go to the closest local minimum.

The IRC was re-run on the chair transition state using 100 points, the results gave the energy as -231.690587 a.u. and the point group was C2/C1. Again the strucure looks like gauche 2.

The IRC was re-run, using 50 points, but with the force constant calculated at every step. The results gave the energy as -231.652401 a.u, the point group was C2/C1. Only 14 of the 50 points were run so this isn't the final minismised geometry.

Resulting molcecule from IRC using 50 points
Resulting molecule from optimising result from first IRC
Resulting molcecule from IRC using 100 points
Resulting molecule from IRC calculating force constants at every step

From this the minimised geometry is and the resulting conformer will be gauche2 as the energy values and the pictures match that conformer.

Both transition states were reoptimised using the B3LYP/6-31G* method and basis set. The chair transition state returned the results of overall energy as -234.5569 a.u. The zero-point energies are -234.41503 (147096.134kcal/mol). The energies at 298.15K are -234.40906 (147092.390kcal/mol). These values are much lower than the previous results but the pictures still look very similar. The higher optimisation didn't work for the boat transition state, many different approaches were taken but all the calculations ended abnormally.

Using the values obtained from the higher optimisation of the reactant (the anti2 conformation of 1,5-hexadiene) and the chair transtition state, activation energies have been calculated. The activation energy at 0K is computed at 33.98 kcal/mol. The activation energy at 298.15K is computed at 33.12kcal/mol. These values are very close to the experimental value of 33.5 ± 0.5kcal/mol at 0K.

Chair Transition State
Animated Imaginary Vibration for the chair transition state
Boat Transition State
Animated Imaginary Vibration fo the boat transition state

The Diels-Alder Cycloaddition

Cis-Butadiene

A molecule of cis-butadiene underwent optimisation and frequency analysis. The energy of the molecule was -154.05394 a.u. The HOMO and LUMO molecular orbitals were visualised and the HOMO was anti-symmetric and the LUMO was symmetric.

Cis-butadiene
Cis-butadiene - HOMO
Cis-butadiene - LUMO
Ethylene - HOMO
Ethylene - LUMO

Computing the Transtion State

A transition state was computed for the reaction between cis-butadiene and ethylene. This was done by building two fragments one of CH2CHCHCH2 and one of CH2CH2 and positioning them in an envelope type structure. The geometries were then optimised using the redundant coordinate editor to freeze the coordinates and then to derivitise the bond lengths.

The results showed that the energy of the first transition state was -231.603206 a.u., with the bond lengths between the bonding carbons as 2.20583 and 2.21241 angstroms. There is an imaginary vibration at -818.135cm-1.

To determine if the correct transition state had been computed, the imaginary vibration was visualised to see if it followed the diels alder mechansim of the bonding carbons moving towards each other in a concerted fashion, in this case it did so was the correct structure. The HOMO and LUMO orbitals of the transition state were visualised, there should be good overlap between the pi orbitals of ethylene and cis-butadiene. As noted before the HOMO of cis-butadiene is anti-symmetric and the LUMO is symmetric. The HOMO of ethylene is symmetric and the LUMO is anti-symmetric. As only molecular orbitals of the same symmetry can overlap to allow the reaction to occur, the HOMO of cis-butadiene and the LUMO of ethylene wil interact and vice versa. The resulting HOMO and LUMO are both symmetric.

Typical C-C (sp3 hybridised) bonds are 154 pm. Typical C-C (sp2 hybridised) bonds are 135 pm, they are shorter than the sp3 hybridised bonds because there is greater s character in the orbitals. The van der waals radius of carbon is 1.70 angstrom. Taking these values into consideration and looking at the transition state, the partially formed carbon bonds are longer than all these values, which shows there is very little interaction in the transition state stage, which indicates that it is an early transition state and is reactant-like.

The imaginary vibration shows the carbons moving together in a synchronous manner. This indicates that the bonds will be formed at the same time. The lowest positive vibration at 164.88cm-1 shows the ethylene fragment rocking to and from the cis-butadiene fragment at opposite times in an asynchronous manner.

The HOMO of the transition state is symmetric and involves the interaction of the LUMO of cis-butadiene and the HOMO of ethylene (both symmetric). This reaction is allowed because the interaction is between the HOMO of one molecule and the LUMO of another that both have the same symmetry. This results in good orbital overlap and hence new bonds can be formed. If the orbitals were of opposite symmetry, there would be no overlap density so the reaction would be forbidden as no bonds would be made.

Diels Alder Transition State
Diels Alder Transition State Vibration
Diels Alder Transition State - HOMO
Diels Alder Transition State - LUMO

Regioselectivity of Diels Alder

The reaction between cyclohexa-1,3-diene and maleic anhydride is to be studied to observe the regioselectivity of the diels alder cycloaddition. This reaction primarily gives the endo product and is supposedly kinetically controlled so the eno transition state should be lower in energy. The transition states were obtained by building the reactant molecules and optimising separately, and then arranging them together with the diene postioned to react with the dienophile. The difference between the exo and endo state depends on the direction in which the diene (cyclohexa-1,3-diene) attacks the dienophile (maleic anhydride). The transition states were then optimised using the same method as before. The homo of cyclohexadiene and the lumo of maleic anhydride are both anti-symmetric so will interact together. The lumo of cyclohexadiene and the homo of maleic anhydride are both symmetric so will interact together.

Cycohexadiene - HOMO
Cyclohexadiene - LUMO
Maleic Anhydride - HOMO
Maleic Anhydride - LUMO

Th exo transition state had an energy of -605.603591. The lengths of the partially formed carbon single bonds are 2.2609 and 2.2607 angstrom. The distance between the oxygen on the maleic anhydride and the bridging carbons is about 3.188 angstrom. There is an imaginary vibration at -647.409cm-1, which shows the bonding carbons moving towards each other in a concerted fashion. The alkene bonds on the ring are 1.370 angstrom long, the bonds next to them but not joining them are 1.519 angstrom long. The bond joining the double bonds is 1.398 angstrom and the bond opposite this is 1.559 angstrom long. The double bond on the maleic anhydride is 1.373 angstrom and the bonds next to it are 1.481 angstrom. The carbon oxygen ring bonds are 1.396 angstrom and the carbonyl groups are 1.191 angstrom.

From the pictures of the molecular orbitals of the exo transition state it is seen that the HOMO is made up of interaction between the LUMO of maleic anhydride and the HOMO of the cyclohexdiene ring. It is anti-symmetric. There is only interaction between the orbitals at the double bond on the maleic anhydride and the cyclohexadiene ring.

Exo Transition State
Exo Transition State Vibration
Exo Transition State - HOMO
Exo Transition State - LUMO

The endo transition state had an energy of -605.610368. The lengths of the partially formed carbon single bonds are 2.2309 and 2.2311 angstrom. The distance between the oxygen of the maleic anhydride and and the carbon double bond in the ring is 3.1000angstrom. There is an imaginary vibration at -643.437cm-1, which shows the bonding carbons moving towards each other in a concerted fashion. The alkene bonds on the ring are 1.371 angstrom long, the bonds next to them but not joining them are 1.518 angstrom long. The bond joining the double bonds is 1.396 angstrom and the bond opposite this is 1.560 angstrom long. The double bond on the maleic anhydride is 1.370 angstrom and the bonds next to it are 1.481 angstrom. The carbon oxygen ring bonds are 1.394 angstrom and the carbonyl groups are 1.192 angstrom.

From the pictures of the molecular orbitals of the exo transition state it is seen that the HOMO is made up of interaction between the LUMO of maleic anhydride and the HOMO of the cyclohexdiene ring. It is anti-symmetric. There is interaction between the orbitals over the double bonds on the cyclohexadiene ring and the C-C bonds on the maleic anhydride as they are at the correct orientation for interaction to occur, this is secondary orbital overlap and helps to stabilise the structure.

Endo Transition State
Endo Transition State Vibration
Endo Transition State - HOMO
Endo Transition State - LUMO

The resulting energies of the transtion states show that the endo transition state is more stable than the exo strucutre by 0.006777 a.u., this shows that the favoured product will be the endo product. Sterically, the exo structure is less hindered as there is a greater distance between the bridging carbons and the maleic anhydride group compared to the double bonded ring carbons and the maleic anhydride group in the endo structure.

As shown before the average C-C bond length is 1.54 angstrom and the average C=C bond length is 1.35 angstrom. From the above values from the transition state structures, the values for both are pretty similar. The partially formed bonds between the two molecules are slightly longer for the exo structure, which shows the interactions are weaker. All of the carbon double bonds (those on the cyclohexadiene ring and the one on the maleic anhydride) are slightly longer than the average C=C bond length and the single bond joining the double bonds on the ring is slighlty shorter than the average C-C bond. This shows that the pi-bond character is being transferred in the transition state, as the double bonds will become single bonds and the mentioned single bond will become a double bond in the final product. This shows that there has been some change in the electronic structure of the reactants at the transition state level and that there is some sort of interaction happening.

Secondary orbital overlap involves the overlap of p-orbitals of substituents on the dienohpile overlapping with the p-orbitals on the diene and results in a more stable transition state. This only occurs in the endo transition state as the reactants are at the right orientation, with the oxygen part of the maleic anhydride over the diene instead of pointed away (exo transtition state).

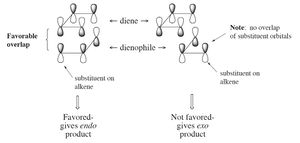
Image taken from: http://www.enc.edu/~timothy.t.wooster/courses/CH322/Lab/3-21%20The%20Diels%20Alder%20reaction.pdf